2020年上海市闵行区部分学校中考数学一模试题无答案版 4页

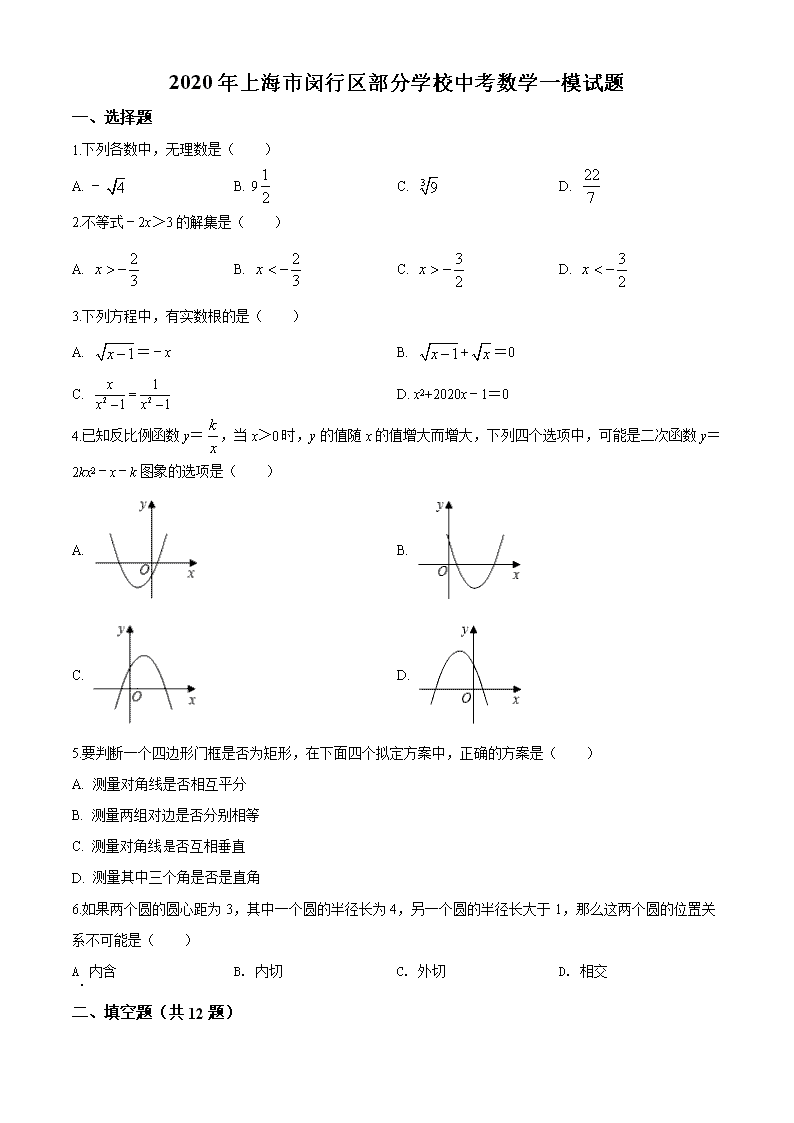
‎2020年上海市闵行区部分学校中考数学一模试题 一、选择题 ‎1.下列各数中，无理数是（　　）‎ A. ﹣ B. 9 C. D. ‎ ‎2.不等式﹣2x＞3的解集是（　　）‎ A. B. C. D. ‎ ‎3.下列方程中，有实数根的是（　　）‎ A. ＝﹣x B. +＝0‎ C. D. x2+2020x﹣1＝0‎ ‎4.已知反比例函数y＝，当x＞0时，y的值随x的值增大而增大，下列四个选项中，可能是二次函数y＝2kx2﹣x﹣k图象的选项是（　　）‎ A. B. ‎ C. D. ‎ ‎5.要判断一个四边形门框是否为矩形，在下面四个拟定方案中，正确的方案是（　　）‎ A. 测量对角线是否相互平分 B. 测量两组对边是否分别相等 C. 测量对角线否互相垂直 D. 测量其中三个角是否是直角 ‎6.如果两个圆的圆心距为3，其中一个圆的半径长为4，另一个圆的半径长大于1，那么这两个圆的位置关系不可能是（　　）‎ A 内含 B. 内切 C. 外切 D. 相交 二、填空题（共12题）‎ ‎7.计算：a2•a3=_____．‎ ‎8.在实数范围内分解因式：______.‎ ‎9.已知f（x）＝2x2﹣1，且f（a）＝3，那么a＝_____．‎ ‎10.已知一次函数y=kx+b的图象如图，则关于x的不等式kx+b＞0的解集是______.‎ ‎11.某同学计划购买一双运动鞋，在网站上浏览时发现如表所示的男鞋尺码对照表．‎ 中码CHN ‎220‎ ‎225‎ ‎230‎ ‎…‎ ‎250‎ ‎255‎ ‎260‎ ‎…‎ 美码USA ‎4.5‎ ‎5‎ ‎5.5‎ ‎…‎ ‎7.5‎ ‎8‎ ‎8.5‎ ‎…‎ 如果美码（y）与中码（x）之间满足一次函数关系，那么y关于x的函数关系式为_____．‎ ‎12.一个不透明的袋子中装有8个大小、形状、都一样的小球，其中有3个红球与5个黄球，从这8个球中任取一个球是红球的概率是：_____．‎ ‎13.如果一段斜坡的坡角是30°，那么这段斜坡的坡度是_______．（请写成1︰m的形式）．‎ ‎14.如图，在△ABC中，AD是边BC上的中线，设向量＝，＝，如果用向量，表示向量，那么向量可以表示为_____．‎ ‎15.已知正三角形的边长为2，那么该三角形的半径长为_____．‎ ‎16.如果两点A（2，a）和B（x，b）在抛物线y＝x2﹣4x+m上，那么a和b大小关系为：a_____b．（从“＞”“≥”“＜”“≤”中选择）．‎ ‎17.平移抛物线y＝2x2﹣4x，可以得到抛物线y＝2x2+4x，请写出一种平移方法_____．‎ ‎18.如果三角形的两个内角∠α与∠β满足2α+β＝90°，那么，我们将这样的三角形称为“准互余三角形”．在△ABC中，已知∠C＝90°，BC＝3，AC＝4（如图所示），点D在AC边上，联结BD．如果△ABD 为“准互余三角形”，那么线段AD的长为_____（写出一个答案即可）．‎ 三、解答题（共7题）‎ ‎19.计算：‎ ‎20.解方程组：‎ ‎21.如图，在△ABC中，∠C＝90°，∠A＝30°，BC＝1，点D在边AC上，且∠DBC＝45°，求sin∠ABD的值．‎ ‎22.某电脑公司2019年的各项经营收入中，经营电脑配件的收入为800万元，占全年经营总收入的40%，该公司预计2021年经营总收入要达到2880万元，且计划从2019年到2021年，每年经营总收入的年增长率相同，问2020年预计经营总收入为多少万元？‎ ‎23.已知：如图，△ABC中，∠ACB＝90°，D在斜边AB上，DE⊥AC，DF⊥BC，垂足分别为E，F．‎ ‎（1）当∠ACD＝∠BCD时，求证：四边形DECF是正方形；‎ ‎（2）当∠BCD＝∠A时，求证：．‎ ‎24.如图，已知一个抛物线经过A（0，1），B（1，3），C（﹣1，1）三点．‎ ‎（1）求这个抛物线的表达式及其顶点D的坐标；‎ ‎（2）联结AB、BC、CA，求tan∠ABC值；‎ ‎（3）如果点E在该抛物线的对称轴上，且以点A、B、C、E为顶点的四边形是梯形，直接写出点E的坐标．‎ ‎25.在圆O中，弦AB与CD相交于点E，且弧AC与弧BD相等．点D在劣弧AB上，联结CO并延长交线段AB于点F，联结OA、OB．当OA＝，且tan∠OAB＝．‎ ‎（1）求弦CD的长；‎ ‎（2）如果△AOF是直角三角形，求线段EF的长；‎ ‎（3）如果S△CEF＝4S△BOF，求线段AF的长．‎