【必刷卷】第七单元 可能性-五年级上册数学单元常考题集训基础卷（一） 北师大版（含答案） 20页

第七单元综合检测基础卷（一） 一．选择题（共 8 小题，满分 16 分，每小题 2 分） 1．（2 分）甲、乙两人做掷骰子游戏，骰子的六个面上分别标有 1、2、3、4、5、6，下面（ ） 游戏规则是公平的． A．质数甲赢，合数乙赢 B．奇数甲赢，偶数乙赢 C．小于 3 的甲赢，大于 3 的乙赢 D．小于 4 的甲赢，大于 4 的乙赢 2．（2 分）将分别标有 1﹣10 的十个相同小球放在一个袋子里，从袋子里任意摸一个球．摸 到质数与合数的可能性相比，（ ） A．摸到质数的可能性大 B．摸到合数的可能性大 C．摸到质数和合数的可能性相等 3．（2 分）把分别写有自然数 1﹣9 的 9 张数字卡片反面扣在桌面，打乱顺序后，任意摸出 一张，摸到（ ）的可能性最大． A．奇数 B．偶数 C．质数 D．合数 4．（2 分）足球比赛通过掷硬币确定谁开球，任意掷一次，下面的说法正确的是（ ） A．正面朝上的可能性大 B．反面朝上的可能性大 C．正、反面朝上的可能性一样大 5．（2 分）从盒子里摸出一个球，一定摸出黑球的是（ ） A． B． C． D． 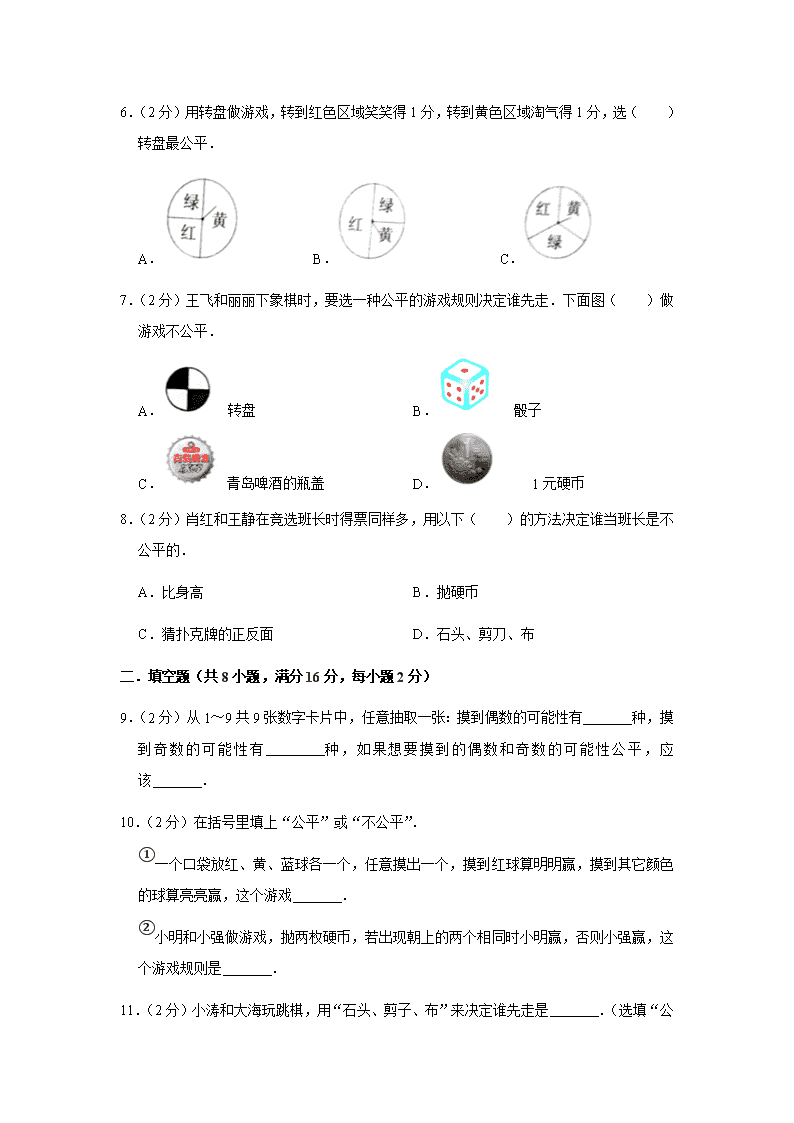6．（2 分）用转盘做游戏，转到红色区域笑笑得 1 分，转到黄色区域淘气得 1 分，选（ ） 转盘最公平． A． B． C． 7．（2 分）王飞和丽丽下象棋时，要选一种公平的游戏规则决定谁先走．下面图（ ）做 游戏不公平． A． 转盘 B． 骰子 C． 青岛啤酒的瓶盖 D． 1 元硬币 8．（2 分）肖红和王静在竞选班长时得票同样多，用以下（ ）的方法决定谁当班长是不 公平的． A．比身高 B．抛硬币 C．猜扑克牌的正反面 D．石头、剪刀、布 二．填空题（共 8 小题，满分 16 分，每小题 2 分） 9．（2 分）从 1～9 共 9 张数字卡片中，任意抽取一张：摸到偶数的可能性有 种，摸 到奇数的可能性有 种，如果想要摸到的偶数和奇数的可能性公平，应该 ． 10．（2 分）在括号里填上“公平”或“不公平”． ① 一个口袋放红、黄、蓝球各一个，任意摸出一个，摸到红球算明明赢，摸到其它颜色 的球算亮亮赢，这个游戏 ． ② 小明和小强做游戏，抛两枚硬币，若出现朝上的两个相同时小明赢，否则小强赢，这 个游戏规则是 ． 11．（2 分）小涛和大海玩跳棋，用“石头、剪子、布”来决定谁先走是 ．（选填“公 平”或“不公平”） 12．（2 分）有红、白、蓝、黄四种颜色的球各 10 个，把它们放在一个不透明的袋子里，摸 出红球的可能性是 ，至少摸出 个球，可以保证摸到两个颜色相同的球． 13．（2 分）一个盒子里装有红色球、黄色球和蓝色球各一个，摸出一个球，是红色球的可 能性是 ． 14．（2 分）一个口袋里放着 5 个彩球和 4 个白球，它们除颜色外完全相同．从中任意摸出 1 个球，摸到白球的可能性是 （填分数）． 15．（2 分）用三张分别写着 2、6、9 的数字卡片，任意摆一个三位数，摆出单数的可能性 比摆出双数的可能性 ．（填“大”或“小”） 16．（2 分）袋子里有 5 个红球、3 个蓝球和 4 个白球，取到蓝球的可能性大小是 ． 三．判断题（共 4 小题，满分 8 分，每小题 2 分） 17．（2 分）一个正方体的各个面上分别写着 1，2，3，4，5，6，掷出落地后，每个数朝上 的可能性相等． （判断对错） 18．（2 分）盒子里有 3 个红球，5 个蓝球，摸到白球的可能性是 0． ．（判断对错） 19．（2 分）投掷一枚硬币 9 次，有 5 次正面向上，4 次反面向上．那么第 10 次投掷这枚硬 币一定反面向上． （判断对错） 20．（2 分）两个小朋友做游戏用抛硬币的方法来决定谁先走，是比较公平的． （判 断对错） 四．应用题（共 4 小题，满分 24 分，每小题 6 分） 21．（6 分）灰太狼在青青草原上看到了喜羊羊和伙伴们在玩游戏，非常兴奋但狡猾的他表 面上露出友善的笑脸走过去，对他们说：“小羊们，我们来做个游戏吧！输的一方什么都 得听赢的一方的．”小羊们虽然不愿意，但也不敢反抗．于是灰太狼公布了游戏规则：“我 拿 1、2、3，你们拿 4、5、6，我们各自任意出一张牌，两张牌的数字相乘积大于 10，就 算本大王赢，等于 10 算平局，小于 10 算你们赢．” （1）灰太狼制定的游戏规则公平吗？ （2）灰太狼一定会赢吗？ 22．（6 分）思思和妙妙做摸球游戏，每次任意摸一个球，然后放回摇勾，每人摸 10 次摸到 白球思思得 1 分，摸到红球妙妙得 1 分，摸到其他颜色的球两人都不得分．你认为从哪 几个盒子里摸球是公平的？ 23．（6 分）有两个正方体，每个面上写上 1、2、3、4、5、6，任意抛这 2 个正方体，他们 的和最可能是几？可能性有多大？ 24．（6 分）一批奖券，号码是 001～125． （1）中二等奖的可能性是多少？ （2）中三等奖的可能性是多少？ 奖别 号码 一等奖 末两位是 25 二等奖 末一位是 0 三等奖 号码中有一个数字是 2 五．操作题（共 3 小题，满分 24 分） 25．（6 分）设计一个转盘，把转盘平均分成 8 份，涂上 3 种颜色，使指针指向红色区域的 可能性最大，指向蓝色区域的可能性最小． 26．（12 分）我是小画家．（按要求涂一涂） （1） 任意摸一个球，一定是红球． （2 任意摸一个球不可能是红球 （3） 任意摸一个球，可能是红球，可能是绿球，也可能是黄球． 27．（6 分）李明和刘军玩一个数字游戏，如果右边的转盘指针指向 2 的整倍数就是李明获 胜，如果指针指向 3 的整倍数就是刘军获胜，请你在如图填上适当的数字，使这个游戏 对双方都公平． 六．解答题（共 2 小题，满分 12 分，每小题 6 分） 28．（6 分）如图几种套圈游戏中，哪种方式更公平，为什么？ 29．（6 分）按左边要求将右边的五角星涂一涂 摸出的一定是黑色． ☆☆☆☆☆ 摸出的可能是黑色． ☆☆☆☆☆ 摸出的不可能是黑色． ☆☆☆☆☆ 第七单元综合检测基础卷（一） 参考答案 一．选择题（共 8 小题，满分 16 分，每小题 2 分） 1．（2 分）甲、乙两人做掷骰子游戏，骰子的六个面上分别标有 1、2、3、4、5、6，下面（ ） 游戏规则是公平的． A．质数甲赢，合数乙赢 B．奇数甲赢，偶数乙赢 C．小于 3 的甲赢，大于 3 的乙赢 D．小于 4 的甲赢，大于 4 的乙赢 【答案】见试题解答内容 【分析】骰子有六个面，标有六个数字：1、2、3、4、5、6；其中质数有 2、3、5；合数 有 4、6；奇数有 1、3、5；偶数有 2、4、6；小于 3 的数有：1、2；大于 3 的数有：4、5、 6；小于 4 的数有：1、2、3；大于 4 的数有：5、6；然后根据可能性的求法逐项判断即 可． 【解答】解：根据上面的分析： A、甲赢的可能性为：3÷6＝ ，乙赢的可能性为：2÷6＝ ， ＞ ，所以游戏规则不 公平； B、甲赢的可能性为：3÷6＝ ，乙赢的可能性为：3÷6＝ ， ，所以游戏规则公 平； C、甲赢的可能性为：2÷6＝ ，乙赢的可能性为：3÷6＝ ， ，所以游戏规则 不公平； D、甲赢的可能性为：3÷6＝ ，乙赢的可能性为：2÷6＝ ， ＞ ，所以游戏规则是 不公平． 故选：B． 2．（2 分）将分别标有 1﹣10 的十个相同小球放在一个袋子里，从袋子里任意摸一个球．摸 到质数与合数的可能性相比，（ ） A．摸到质数的可能性大 B．摸到合数的可能性大 C．摸到质数和合数的可能性相等 【答案】B 【分析】在 1～10 这十个数字中，质数有 2、3、5、7 共 4 个数字，合数有 4、6、8、9、 10 共 5 个数字，4＜5，所以摸到合数的可能性大；据此解答即可． 【解答】解：在 1～10 这十个数字中 质数有 2、3、5、7 共 4 个数字，合数有 4、6、8、9、10 共 5 个数字 4＜5，所以摸到合数的可能性大 故选：B． 3．（2 分）把分别写有自然数 1﹣9 的 9 张数字卡片反面扣在桌面，打乱顺序后，任意摸出 一张，摸到（ ）的可能性最大． A．奇数 B．偶数 C．质数 D．合数 【答案】A 【分析】在 1～9 中，奇数有：1、3、5、7、9 共有 5 个；偶数有：2、4、6、8 共有 4 个； 质数有：2、3、5、7 共有 4 个；合数有：4、6、8、9 共有 4 个；再根据各种数卡片的张 数多少，直接判断可能性的大小即可． 【解答】解：在 1～9 中，奇数有：1、3、5、7、9 共有 5 个；偶数有：2、4、6、8 共有 4 个；质数有：2、3、5、7 共有 4 个；合数有：4、6、8、9 共有 4 个 5＞4＝4＝4 所以摸到奇数的可能性最大 故选：A． 4．（2 分）足球比赛通过掷硬币确定谁开球，任意掷一次，下面的说法正确的是（ ） A．正面朝上的可能性大 B．反面朝上的可能性大 C．正、反面朝上的可能性一样大 【答案】见试题解答内容 【分析】根据常识知识可知，每枚硬币都有正反两个面，任意掷一次，正面朝上和反面 朝上的可能性是一样的．据此解答． 【解答】解：根据分析可知，任意掷一次，正、反面朝上的可能性一样大． 故选：C． 5．（2 分）从盒子里摸出一个球，一定摸出黑球的是（ ） A． B． C． D． 【答案】见试题解答内容 【分析】要想一定是黑球，则所有球的颜色都是黑色．据此解答． 【解答】解：要想一定是黑球，则所有球的颜色都是黑色， 因为 A 盒子中的球都是黑球，所以，在 A 盒子里一定摸到黑球． 故选：A． 6．（2 分）用转盘做游戏，转到红色区域笑笑得 1 分，转到黄色区域淘气得 1 分，选（ ） 转盘最公平． A． B． C． 【答案】见试题解答内容 【分析】根据题意，要想使游戏规则公平，指针停在红色区域和黄色区域的可能性应该 一样，看各转盘的红色区域和黄色区域占整体的多少，再进行比较即可得出答案 【解答】解：第一个转盘，黄色占整个圆的 ，红色和绿色各占 ，所以停在红色和黄 色的可能性不相等，游戏规则不公平； 第二个转盘，红色占整个圆的 ，黄色和绿色各占 ，所以停在红色和黄色的可能性不 相等，游戏规则不公平； 第三个转盘，把整个圆平均分成 3 份，红色、黄色、蓝色各占一份，所以转到红色和黄 色的可能性都是 ，游戏公平； 故选：C． 7．（2 分）王飞和丽丽下象棋时，要选一种公平的游戏规则决定谁先走．下面图（ ）做 游戏不公平． A． 转盘 B． 骰子 C． 青岛啤酒的瓶盖 D． 1 元硬币 【答案】见试题解答内容 【分析】要使游戏公平，那么转到各种结果的可能性大小要相同，由此对各选项进行分 析，解决问题即可． 【解答】解：A 转盘平均分成 4 份，其中 2 份涂色，2 份不涂色，所以转到涂色部分和不 涂色部分的可能性相等，游戏规则公平； B 骰子转到六个面的可能性是一样的，所以游戏规则公平； C 虽然青岛啤酒的瓶盖是两面，但是质地不同，所以抛出正反面的可能性不同，游戏规 则不公平； D 硬币抛出正反两面的可能性一样，游戏规则公平． 所以不公平的是 C 青岛啤酒的瓶盖． 故选：C． 8．（2 分）肖红和王静在竞选班长时得票同样多，用以下（ ）的方法决定谁当班长是不 公平的． A．比身高 B．抛硬币 C．猜扑克牌的正反面 D．石头、剪刀、布 【答案】见试题解答内容 【分析】如果两人身高不同，用比身高的方法确定谁当班长等于量身定做，是不公平的； 抛出的硬币落下时，只有两种可能，规则公平；猜扑克牌的正反，扑克牌只有反、正面， 对两人的也是公平的；石头、剪刀、布谁赢的可能性是相同的，规则公平． 【解答】解：肖红和王静在竞选班长时得票同样多，用比身高的方法决定谁当班长是不 公平的． 故选：A． 二．填空题（共 8 小题，满分 16 分，每小题 2 分） 9．（2 分）从 1～9 共 9 张数字卡片中，任意抽取一张：摸到偶数的可能性有 4 种，摸到 奇数的可能性有 5 种，如果想要摸到的偶数和奇数的可能性公平，应该 拿走一张奇 数卡片或再添一张偶数卡片 ． 【答案】见试题解答内容 【分析】在 1～9 共 9 张数字卡片中，偶数有：2、4、6、8 四个，所以摸到偶数的可能性 有 4 种；奇数有：1、3、5、7、9 五个，所以摸到奇数的可能性有 5 种；要想摸到的偶 数和奇数的可能性公平，可以拿走一张奇数卡片或再添一张偶数卡片． 【解答】解：从 1～9 共 9 张数字卡片中，任意抽取一张：摸到偶数的可能性有 4 种，摸 到奇数的可能性有 5 种，如果想要摸到的偶数和奇数的可能性公平，应该拿走一张奇数 卡片或再添一张偶数卡片． 故答案为：4；5；拿走一张奇数卡片或再添一张偶数卡片． 10．（2 分）在括号里填上“公平”或“不公平”． ① 一个口袋放红、黄、蓝球各一个，任意摸出一个，摸到红球算明明赢，摸到其它颜色 的球算亮亮赢，这个游戏 不公平 ． ② 小明和小强做游戏，抛两枚硬币，若出现朝上的两个相同时小明赢，否则小强赢，这 个游戏规则是 公平 ． 【答案】见试题解答内容 【分析】 ① 一个口袋放红、黄、蓝球各一个，共 1+1+1＝3（个）球，任意摸出一个，摸 到红球的可能性是 ，摸到其它颜色的球的可能性是 ． ＜ ，明明赢的可能性小于 亮亮赢的可能性，规则不公平． ② 抛出的硬币只有两种可能，要么正面朝上，要么反而朝上，各占 ．小明和小强做游 戏，抛两枚硬币，若出现朝上的两个相同时小明赢，否则小强赢，这个游戏规则公平． 【解答】解： ① 一个口袋放红、黄、蓝球各一个，任意摸出一个，摸到红球算明明赢， 摸到其它颜色的球算亮亮赢，这个游戏不公平． ② 小明和小强做游戏，抛两枚硬币，若出现朝上的两个相同时小明赢，否则小强赢，这 个游戏规则是公平． 故答案为：不公平，公平． 11．（2 分）小涛和大海玩跳棋，用“石头、剪子、布”来决定谁先走是 公平 ．（选填“公 平”或“不公平”） 【答案】见试题解答内容 【分析】用“石头、剪子、布”决定谁先走，判断是否公平的关键是看出现的概率是否 一样，如果出现的概率一样就公平，如果不一样那就不公平． 【解答】解：用“石头、剪子、布”决定谁先走， 因为小涛和大海出石头、剪子、布这三种情况出现的机会是均等的， 小涛获胜的可能性：1÷3＝ ， 大海获胜的可能性：1÷3＝ ， 所以说很公平． 故答案为：公平． 12．（2 分）有红、白、蓝、黄四种颜色的球各 10 个，把它们放在一个不透明的袋子里，摸 出红球的可能性是 ，至少摸出 5 个球，可以保证摸到两个颜色相同的球． 【答案】见试题解答内容 【分析】有红、白、蓝、黄四种颜色的球各 10 个，求摸到红球的可能性，根据可能性的 求法：即求一个数是另一个数的几分之几用除法解答；由于袋子里共有红、绿、黑、白 四种颜色的球各 10 个，如果一次取 4 个，最差情况为红、白、蓝、黄四种颜色只摸出一 种颜色，所以只要再多取一个球，就能保证取到两个颜色相同的球，即 4+1＝5 个；据此 解答． 【解答】解：10÷（10+10+10+10） ＝10÷40 ＝ 最差情况为：先摸出 4 个不相同颜色的球，所以只要再多取一个球，就能保证取到两个 颜色相同的球，即 4+1＝5（个） 答：摸出红球的可能性是 ，至少摸出 5 个球，可以保证摸到两个颜色相同的球． 故答案为： ，5． 13．（2 分）一个盒子里装有红色球、黄色球和蓝色球各一个，摸出一个球，是红色球的可 能性是 ． 【答案】见试题解答内容 【分析】一共有 3 个球，用红色球的数量除以球的总数量即可求解． 【解答】解：1÷（1×3）＝ 答：摸出一个球，是红色球的可能性是 ． 故答案为： ． 14．（2 分）一个口袋里放着 5 个彩球和 4 个白球，它们除颜色外完全相同．从中任意摸出 1 个球，摸到白球的可能性是 （填分数）． 【答案】见试题解答内容 【分析】先求出两种球的总量；然后根据求可能性的方法：求一个数是另一个数的几分 之几，用除法列式解答，用白球的数量除以球的总量，求出摸到白球的可能性是多少即 可． 【解答】解：4÷（5+4） ＝4÷9 ＝ 答：摸到白球的可能性是 ． 故答案为： ． 15．（2 分）用三张分别写着 2、6、9 的数字卡片，任意摆一个三位数，摆出单数的可能性 比摆出双数的可能性 小 ．（填“大”或“小”） 【答案】见试题解答内容 【分析】根据单数（奇数）、双数（偶数）的意义，不是 2 的倍数的数是单数（奇数）； 是 2 的倍数的数是双数（偶数）．再根据简单的排列组合的方法，用 2、6、9 三张数字卡 片组成的三位数有：269、296、629、692、926、962；其中单数有 269、629 两个，双数 有 296、692、926、962 四个，由事件发生的可能性得：摆出单数的可能性是 ，摆出双 数的可能性是 ，据此解答即可． 【解答】解：用 2、6、9 三张数字卡片组成的三位数有：269、296、629、692、926、962 共六个； 其中单数有 269、629 两个，双数有 296、692、926、962 四个， 摆出单数的可能性是 2÷6＝ ，摆出双数的可能性是 4÷6＝ ， 答：摆出单数的可能性比摆出双数的可能性小． 故答案为：小． 16．（2 分）袋子里有 5 个红球、3 个蓝球和 4 个白球，取到蓝球的可能性大小是 ． 【答案】见试题解答内容 【分析】先“3+4+5＝12”求出袋子中的球的个数，求摸到蓝球的可能性，根据可能性的 求法：即求一个数（3）是另一个数（12）的几分之几用除法解答即可． 【解答】解：3÷（3+4+5） ＝3÷12 ＝ 答：取到蓝球的可能性大小是 ． 故答案为： 三．判断题（共 4 小题，满分 8 分，每小题 2 分） 17．（2 分）一个正方体的各个面上分别写着 1，2，3，4，5，6，掷出落地后，每个数朝上 的可能性相等． √ （判断对错） 【答案】见试题解答内容 【分析】因为共 6 个数字，每个数字都有 1 个，求掷出每个数字的可能性，根据可能性 的求法：即求一个数是另一个数的几分之几，用除法解答即可． 【解答】解：掷出每个数字的可能性：1÷6＝ ， 即每个数朝上的可能性都是 ，所以原题说法正确． 故答案为：√． 18．（2 分）盒子里有 3 个红球，5 个蓝球，摸到白球的可能性是 0． √ ．（判断对错） 【答案】见试题解答内容 【分析】根据题意，可得盒子里白球的数量是 0，所以根据随机事件发生的可能性，可得 摸到白球的可能性是 0，据此解答即可． 【解答】解：因为盒子里有 3 个红球，5 个蓝球， 所以盒子里白球的数量是 0， 所以摸到白球的可能性是 0． 故答案为：√． 19．（2 分）投掷一枚硬币 9 次，有 5 次正面向上，4 次反面向上．那么第 10 次投掷这枚硬 币一定反面向上． × （判断对错） 【答案】见试题解答内容 【分析】判断正面朝上的可能性，要看一共有几种可能发生的情况，用 1 除以总数，即 可得到发生的可能性． 【解答】解：因为硬币有两个面：一个正面、一个反面， 所以，可能发生的情况只有两种， 反面朝上与反面朝上的可能性都是：1÷2＝ ，所以抛 9 次硬币，可有 5 次正面向上，4 次反面向上， 第 10 次投掷这枚硬币一定反面向上，说法错误； 故答案为：×． 20．（2 分）两个小朋友做游戏用抛硬币的方法来决定谁先走，是比较公平的． √ （判 断对错） 【答案】见试题解答内容 【分析】投出的硬币落下后只有两种可能，要么正面朝上要么反面朝上，每种可能性都 占 ，因此，游戏规则公平；据此解答即可． 【解答】解：两个小朋友做游戏用抛硬币的方法来决定谁先走，要么正面朝上要么反面 朝上，每种可能性都占 ，是比较公平的． 原题说法正确． 故答案为：√． 四．应用题（共 4 小题，满分 24 分，每小题 6 分） 21．（6 分）灰太狼在青青草原上看到了喜羊羊和伙伴们在玩游戏，非常兴奋但狡猾的他表 面上露出友善的笑脸走过去，对他们说：“小羊们，我们来做个游戏吧！输的一方什么都 得听赢的一方的．”小羊们虽然不愿意，但也不敢反抗．于是灰太狼公布了游戏规则：“我 拿 1、2、3，你们拿 4、5、6，我们各自任意出一张牌，两张牌的数字相乘积大于 10，就 算本大王赢，等于 10 算平局，小于 10 算你们赢．” （1）灰太狼制定的游戏规则公平吗？ （2）灰太狼一定会赢吗？ 【答案】见试题解答内容 【分析】（1）在 1、2、3 与 4、5、6 和乘积中有 1×4＝4、1×5＝5，1×6＝6、2×4＝8、 2×5＝10、2×6＝12、3×4＝12、3×5＝16、3×6＝18，其中小于 10 的只有 4 可能，等 于 10 的只有 1 种可能，大于 10 的有 4 种可能．小羊们和灰太狼赢（或输入）的可能性 相等，这个游戏规则公平． （2）既然游戏规则公平，小羊位、灰太狼赢的可能性相等，因此，灰大狼不一定会赢． 【解答】解：（1）1、2、3 与 4、5、6 和乘积中有 1×4＝4、1×5＝5，1×6＝6、2×4＝ 8、2×5＝10、2×6＝12、3×4＝12、3×5＝16、3×6＝18 其中小于 10 的只有 4 可能，等于 10 的只有 1 种可能，大于 10 的有 4 种可能 小羊们、灰太狼赢的可能性相等，都占 游戏规则公平． （2）小羊们、灰太狼赢的可能性相等，都占 ，戏规则公平，灰大狼不一定会赢． 22．（6 分）思思和妙妙做摸球游戏，每次任意摸一个球，然后放回摇勾，每人摸 10 次摸到 白球思思得 1 分，摸到红球妙妙得 1 分，摸到其他颜色的球两人都不得分．你认为从哪 几个盒子里摸球是公平的？ 【答案】见试题解答内容 【分析】根据题意，若要使游戏公平，则摸到红球和白球的可能性应该是一样的，也就 是红球和白球的数量应该是相等的．据此解答． 【解答】解：2＝2 因为第一个盒子中红球和白球的数量相等，所以从第一个盒子里摸球是公平的． 5＞4 所以第二个盒子中摸到红球和白球的可能性不相等，游戏不公平． 3＞0 所以第三个盒子中摸到白球和摸到红球的可能性不相等，游戏规则不公平． 3＝3 所以第四个盒子中的红球和白球个数相等，摸到的可能性也相等，游戏规则公平． 答：从第一个和第四个盒子中摸，游戏规则是公平的． 23．（6 分）有两个正方体，每个面上写上 1、2、3、4、5、6，任意抛这 2 个正方体，他们 的和最可能是几？可能性有多大？ 【答案】见试题解答内容 【分析】一个正方体的面上的数字可能 1、2、3、4、5、6 共 6 种可能，另一个正方体面 上的数字同样有 1、2、3、4、5、6 共 6 种可能，根据乘法原理，有 6×6＝36 种可能性， 和的值有重复，列表后，数一数，从 2 到 12 共 11 种，再根据和出现次数的多少判断可 能性的大小，据此得解． 【解答】解：列表得： 1+6＝7 2+6＝8 3+6＝9 4+6＝10 5+6＝11 6+6＝12 1+5＝6 2+5＝7 3+5＝8 4+5＝9 5+5＝10 6+5＝11 1+4＝5 2+4＝6 3+4＝7 4+4＝8 5+4＝9 6+4＝10 1+3＝4 2+3＝5 3+3＝6 4+3＝7 5+3＝8 6+3＝9 1+2＝3 2+2＝4 3+2＝5 4+2＝6 5+2＝7 6+2＝8 1+1＝2 2+1＝3 3+1＝4 4+1＝5 5+1＝6 6+1＝7 和是 6，8 时出现 5 次，7 时出现 6 次，所以和是 6，7，8 的可能性大； 6÷（6×6） ＝6÷36 ＝ ； 答：他们的和最可能是 6、7、8；可能性是 ． 24．（6 分）一批奖券，号码是 001～125． （1）中二等奖的可能性是多少？ （2）中三等奖的可能性是多少？ 奖别 号码 一等奖 末两位是 25 二等奖 末一位是 0 三等奖 号码中有一个数字是 2 【答案】见试题解答内容 【分析】（1）一共有 125 个数，能中二等奖的数字有：10、20…90、100、110、120，一 共有 12 个．中二等奖的可能性是 12÷125． （2）一共有 125 个数，能中三等奖的数字有：2、12、22、32…92、102、112、122，一 共有 13 个．中二等奖的可能性是 13÷125． 【解答】解：（1）符合二等奖的数字个数除以总数，就是获得二等奖的可能性：12÷125 ＝ ． （2）符合三 等奖的数字个数除以总数，就是获得三等奖的可能性：13÷125＝ ． 五．操作题（共 3 小题，满分 24 分） 25．（6 分）设计一个转盘，把转盘平均分成 8 份，涂上 3 种颜色，使指针指向红色区域的 可能性最大，指向蓝色区域的可能性最小． 【答案】见试题解答内容 【分析】根据指针指向区域的可能性就是所指区域的面积与总面积的比即可解答．使红 色区域的面积最大，则转动转盘待停止后指针指向红色区域的可能性最大；使蓝色区域 的面积最小，则转动转盘待停止后指针指向蓝色区域的可能性最小． 【解答】解：如图： 26．（12 分）我是小画家．（按要求涂一涂） （1） 任意摸一个球，一定是红球． （2 任意摸一个球不可能是红球 （3） 任意摸一个球，可能是红球，可能是绿球，也可能是黄球． 【答案】见试题解答内容 【分析】（1）只要盒子里全部是红球，摸出的一定是红球； （2）盒子里没有红球，摸出的不可能是红球； （3）盒子里有黄球，还有红球，也有绿球，所以任意摸一个球，可能是红球，可能是绿 球，也可能是黄球；据此画图即可． 【解答】解：根据题干分析可得： 27．（6 分）李明和刘军玩一个数字游戏，如果右边的转盘指针指向 2 的整倍数就是李明获 胜，如果指针指向 3 的整倍数就是刘军获胜，请你在如图填上适当的数字，使这个游戏 对双方都公平． 【答案】见试题解答内容 【分析】要使这个游戏对双方都公平，那么 2 的倍数所占的圆的区域就要和 3 的倍数所 占的区域相同，由图可以看出左右的四个面积大小相同，上下的面积大小相同，分别把 它们平均分开即可． 【解答】解：2 的倍数可填 4，8，10；3 的倍数可填 3，9，15.6 和 12 等即使 3 的倍数也 是 2 的倍数无法判定谁获胜，不采用．填法如下： 六．解答题（共 2 小题，满分 12 分，每小题 6 分） 28．（6 分）如图几种套圈游戏中，哪种方式更公平，为什么？ 【答案】见试题解答内容 【分析】同学距离目标的远近不同，会有不同的效果，距离越近越准确，套中的可能性 越大，逐个分析，即可得解． 【解答】解：（1）组同学站在一条线上，被套圈的目标离他们的远近不同，需要用力的 大小就不一样，所以不公平； （2）组同学围成一个正方形，目标靠近无人的一边，导致对边的同学距离大，所以不公 平； （3）组同学围成一个圆，目标在圆心上，他们距离目标大小都是圆的半径，所以最公平． 答：第（3）组的方式最公平． 29．（6 分）按左边要求将右边的五角星涂一涂 摸出的一定是黑色． ☆☆☆☆☆ 摸出的可能是黑色． ☆☆☆☆☆ 摸出的不可能是黑色． ☆☆☆☆☆ 【答案】见试题解答内容 【分析】 ① 摸出的一定是黑色，即可能性是 1，属于确定事件中的必然事件，只要把五 角星都化成黑色即可； ② 摸到的可能是黑色，属于不确定事件中的可能性事件，所以只要在 5 个五角星中有黑 色的即可； ③ 摸出的不可能是黑色，属于确定事件中的不可能事件，可能性是 0，即在 5 个五角星 中没有黑色的即可． 【解答】解：