小学五年级奥数教案：分数与小数的混合运算(学生版) 8页

学科培优 数学 “分数与小数的混合运算” 学生姓名 授课日期 教师姓名 授课时长 知识定位 本讲知识点属于计算板块的部分，难度并不大。要求学生在运算顺序正确的 前提下，通过一定题目的训练，熟练把握分数和小数之间的互化，从而使题目化 繁为简。 知识梳理 一、分数和小数的定义： 分数：表示把一个“单位 1”平均分成若干份，取其中的一份或几份的数， 叫做分数 （分成零份在此不讨论） 分数又分为真分数、假分数和带分数。 真分数：分子比分母小的分数叫真分数。 假分数：分子比分母大，或者分子等于分母的分数叫做假分数。（分母、分 子为零在此不讨论） 带分数：一个整数（零除外）和一个真分数组合在一起的数，叫做带分数。 带分数也是假分数的另一种表示形式，相互之间可以互化。 小数：分母是 10n 的（n 为自然数）分数叫做“十进分数”。由于任何一个 “十进分数”都能写成小数的形式，例如：7/10＝0.7，7/10^2＝0.07 等等，所 以一般而言，小数是特殊形式的分数。（但是不能说小数就是分数） 小数分为有限小数和循环小数。 一个小数，从小数部分的某一位起，一个数字或几个数字，依次不断地重复 出现，这个小数叫做循环小数。 循环节：一个循环小数的小数部分，依次不断重复出现的数字 叫做这个循环小数的循环节。例如：0.3333……循环节是“3” 2.14242……循环节是“42” 二、分数与小数混合运算时的运算顺序： 在整数四则混合运算中，有加、减法，又有乘、除法，要先算乘、除法，后 算加、减法；有小括号、中括号、大括号的，要先算小括号，再算中括号，最后 算大括号。 【授课批注】 高年级同学有时会遇到幂的运算——即：2 次方或者 3 次方等，做题时，应首先 进行括号的运算，然后是幂，后面才是乘除和加减。 三、分数与小数混合运算的技巧： 在分数、小数的四则混合运算中，到底是把分数化成小数，还是把小数化成 分数，这不仅影响到运算过程的繁琐与简便，也影响到运算结果的精确度，因此， 要具体情况具体分析，而不能只机械地记住一种化法：小数化成分数，或分数化 成小数。 技巧 1：一般情况下，在加、减法中，分数化成小数比较方便。 技巧 2：在加、减法中，有时遇到分数只能化成循环小数时，就不能把分数化成 小数。此时要将包括循环小数在内的所有小数都化为分数。 【授课批注】 技巧 2 中提到的循环小数化分数会在题目中具体进行讲解。 技巧 3：在乘、除法中，一般情况下，小数化成分数计算，则比较简便。 技巧 4：在运算中，使用假分数还是带分数，需视情况而定。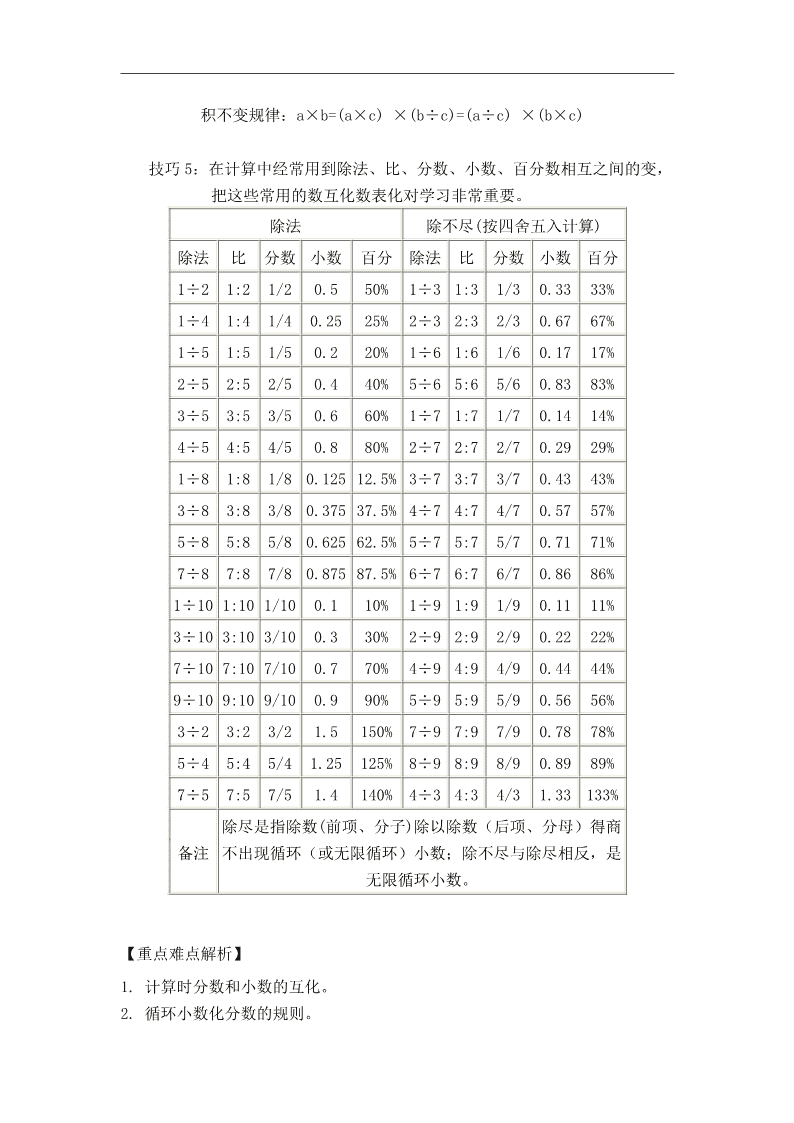 【授课批注】 加法交换律：a+b=b+a 加法结合律：(a+b)+c=a+(b+c) 和不变规律：a+b=(a+c)+(b-c)=(a-c)+(b+c) 减法的性质：a-b-c=a-(b+c) (a-b)+(c-d)=(a-d)+(c-b) (a>d,c>b) 差不变规律：a-b=(a-c)-(b-c)=(a+c)-(b+c) 乘法交换率：a×b=b×a 乘法结合率：(a×b) ×c=a×(b×c) 乘法分配率：(a+b) ×c=a×c+b×c 积不变规律：a×b=(a×c) ×(b÷c)=(a÷c) ×(b×c) 技巧 5：在计算中经常用到除法、比、分数、小数、百分数相互之间的变， 把这些常用的数互化数表化对学习非常重要。 除法 除不尽(按四舍五入计算) 除法 比 分数 小数 百分 除法 比 分数 小数 百分 1÷2 1:2 1/2 0.5 50% 1÷3 1:3 1/3 0.33 33% 1÷4 1:4 1/4 0.25 25% 2÷3 2:3 2/3 0.67 67% 1÷5 1:5 1/5 0.2 20% 1÷6 1:6 1/6 0.17 17% 2÷5 2:5 2/5 0.4 40% 5÷6 5:6 5/6 0.83 83% 3÷5 3:5 3/5 0.6 60% 1÷7 1:7 1/7 0.14 14% 4÷5 4:5 4/5 0.8 80% 2÷7 2:7 2/7 0.29 29% 1÷8 1:8 1/8 0.125 12.5% 3÷7 3:7 3/7 0.43 43% 3÷8 3:8 3/8 0.375 37.5% 4÷7 4:7 4/7 0.57 57% 5÷8 5:8 5/8 0.625 62.5% 5÷7 5:7 5/7 0.71 71% 7÷8 7:8 7/8 0.875 87.5% 6÷7 6:7 6/7 0.86 86% 1÷10 1:10 1/10 0.1 10% 1÷9 1:9 1/9 0.11 11% 3÷10 3:10 3/10 0.3 30% 2÷9 2:9 2/9 0.22 22% 7÷10 7:10 7/10 0.7 70% 4÷9 4:9 4/9 0.44 44% 9÷10 9:10 9/10 0.9 90% 5÷9 5:9 5/9 0.56 56% 3÷2 3:2 3/2 1.5 150% 7÷9 7:9 7/9 0.78 78% 5÷4 5:4 5/4 1.25 125% 8÷9 8:9 8/9 0.89 89% 7÷5 7:5 7/5 1.4 140% 4÷3 4:3 4/3 1.33 133% 备注 除尽是指除数(前项、分子)除以除数（后项、分母）得商 不出现循环（或无限循环）小数；除不尽与除尽相反，是 无限循环小数。 【重点难点解析】 1. 计算时分数和小数的互化。 2. 循环小数化分数的规则。 【竞赛考点挖掘】 1. 将该类型题目转化为解方程问题。 2. 循环小数化分数。 例题精讲 【试题来源】 【题目】计算 1 25.2 3 1 0.75 3    【试题来源】 【题目】计算 4 50.32 0.37515 9    【试题来源】 【题目】 计算 19971997 19971998  【试题来源】 【题目】计算 19971997 19971998  【试题来源】 【题目】计算 3 8 2 5 718 0.65 18 17 13 7 13 13        【试题来源】 【题目】 解关于 x 的方程 1 1 1( 151 ) 2.4 5 38 3 2 2 x x      【试题来源】 【题目】已知 1 216.2 [(4 700 ) 1 ] 8.17 7    □ ，那么□=_______ 习题演练 【试题来源】 【题目】计算 9.6 89 1103 24 1993 25 1993    【试题来源】 【题目】计算 16 5 258 5931 102 17 33 3 32 512 236 93      【试题来源】 【题目】将下列算式的计算结果写成带分数： 0.5 236 59 119   【试题来源】 【题目】计算 7 4480 8333 ÷ 21934 25909 ÷1 18556 35255 【试题来源】 【题目】计算 1 5 3 2 19(4.85 3.6 6.15 3 ) 5.5 1.75 (1 )4 18 5 3 21             【试题来源】 【题目】计算 141.2 8.1 11 9 537 0.194      【试题来源】 【题目】计算 2 2 5 5(9 7 ) ( )7 9 7 9    【试题来源】 【题目】计算 1 2 3 2 4 6 4 8 12 7 14 21 1 3 5 2 6 10 4 12 20 7 21 35                       【试题来源】 【题目】求下述算式计算结果的整数部分 1 1 1 1 1 1( ) 3852 3 5 7 11 13       【试题来源】 【题目】计算 148 86 7439 148 48149 149 149     【试题来源】 【题目】计算 )1995 6.1 5.01995 4.01993( 22.550 2769 519 22.510 939 519     【试题来源】 【题目】计算 9999 99 99100   【试题来源】 【题目】求□代表的数是多少 2 1 8[(6.5 ) 3 1 ] ( 71.95 103 2 15      □ ） 【试题来源】 【题目】计算 117 1112 1 13 41(6 8 ) (3 3 )665 1995 13 17 221     【试题来源】 【题目】已知 1 8 1 111 12 1 4x     ，则 x 等于多少? 【试题来源】 【题目】计算 1 2.1 0.54 55110 154 0.21 4 5      【试题来源】 【题目】某学生将 1.2 · 3乘以一个数 a 时，把 1.2 · 3误看成 1.23，使乘积比正确结果减少 0.3．则 正确结果该是多少?