五年级上册数学教案-6组合图形面积｜冀教版 (1) 5页

组合图形面积计算 教学内容：‎ 教学目标：‎ ‎1、认识组合图形，能用分割、添补法将组合图形合理转化成已学的基本图形，找准相关数据，利用面积公式列式计算。 ‎ 2、 初步感受部分组合图形可用平移、等积变形方法求面积。‎ ‎3、在自主探索活动中，理解计算组合图形面积方法的多样化，并在解决问题过程中向方法择优化发展。‎ ‎4、在解决实际问题中，感受数学的应用价值。‎ 教学重点：‎ 将组合图形合理转化成已学的基本图形，找准相关数据，利用面积公式列式计算。 ‎ 教学难点：‎ 1、 找准相关数据。‎ 2、 理解方法多样化并向解决问题择优化发展。‎ 教学过程：‎ 一、 课前2分钟微课（复习引新）：‎ 整理你学过的基本图形的面积公式：‎ S长 = S正 = S = S = S梯 =‎ 二、 新知导学：求组合图形的面积。‎ （一） 图片介绍引出组合图形概念：由两个或两个以上基本图形组合而成的平面图形叫组合图形。 ‎ ‎（二）解决问题：求生活中组合图形的面积。‎ ‎1、师：小区建设规划了一块面积建造小花园，如何求面积？‎ 生：可以转化为我们学过的基本图形，就可通过面积公式计算面积。‎ ‎2、师：（学习单）将下面组合图形合理分解成你学过的基本图形，你有几种分解法？（先独立思考完成再小组交流拓展思维） ‎ ‎ ‎ 小组汇报反馈后总结：‎ 生：分割成一个长方形和一个三角形，分割成两个相等的梯形，拼补成一个长方形。‎ 师：组合图形面积基本计算方法：分割求基本图形之和，或添补求基本图形之差。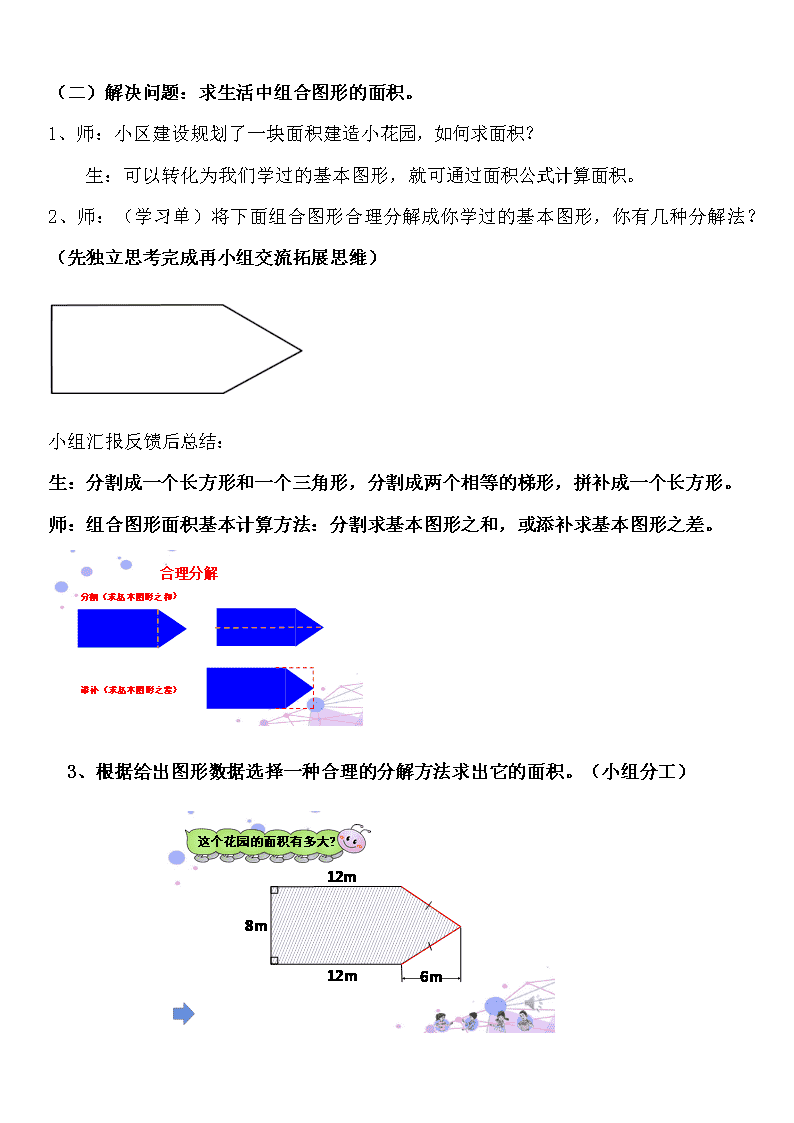‎ ‎3、根据给出图形数据选择一种合理的分解方法求出它的面积。（小组分工） ‎ ‎ ‎ 生反馈，师引导，方法多样化向方法择优化发展。（根据具体图形数据）‎ 方法总结：将组合图形合理分割、添补成已学的基本图形，找准相关数据，利用基本图形面积公式列式计算。‎ 一、 练习巩固：‎ ‎（一）基本练习：求组合图形面积 ‎（二）提高练习：脑洞大开，求组合图形的面积。‎ ‎1、用割补---平移法求组合图形面积：‎ ‎2、用等积变形法求组合图形面积：‎ ‎3、方法总结：‎ 当我们计算的图形面积不能直接计算时，可以合理转化成能计算出面积的基本图形，一般用分割、添补法，有时根据图形、数据特征还可用平移。等积变形的方法灵活计算。‎ ‎（三）拓展：‎ ‎1、数学知识拓展----名人介绍：‎ 中国古代数学家刘徽被称为中国数学史上的牛顿。他利用出入相补原理来计算平面图形的面积。把一个图形经过分割、移补，而面积保持不变，来计算出它的面积。 朱青出入图介绍。‎ ‎2、知识拓展：介绍用平移、等积变形两种方法求例题面积。‎ 一、 课后作业：‎ 1、 尝试平移、等积变形两种方法求例题面积。‎ 2、 分别用割、补两种方法求下图面积。‎ ‎ ‎