六年级上册数学课件-2 比例的基本性质 ｜冀教版 (1) 20页

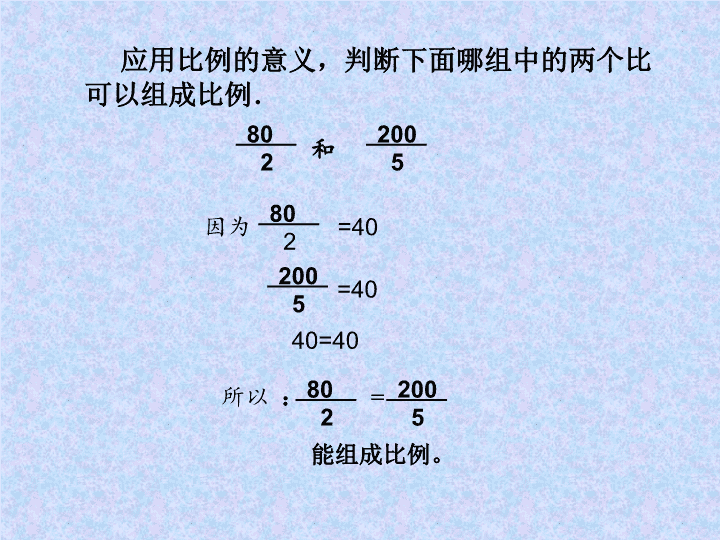
比例的基本性质 应用比例的意义，判断下面哪组中的两个比 可以组成比例． 6∶3 和 8∶5 3∶2 和 0.6∶0.4 所以： 6∶3 和 8∶5 不能组成比例． 所以：能组成比例 3∶2 = 0.6∶0.4 因为： 6∶3 ＝ 2 8∶5 ＝ 2 ≠ 因为： 3∶2= 0.6∶0.4= = 复习导入 应用比例的意义，判断下面哪组中的两个比 可以组成比例． 2 80 5 200 和 2 80 因为 =40 所以 ： = 能组成比例。 5 200 =40 40=40 2 80 5 200 自学问题 2 、比例中有几个项？ 分别叫什么？ 1 、什么叫比例的项？ 组成比例的四个数叫做比例的项 比例中有四个项，两端的两项叫做比例的 外项， 中间的两项叫做比例的内项。 内项 外项 2 . 4 : 1 . 6 ＝ 60 : 40 2.4 ︰ 1.6 60 ︰ 40 ＝ 2.4 1.6 ＝ 60 40 外项 外项 内项 内项 交叉相对 两种形式的比例中四个项及每个项的位置都相同，只是形式不同而已，因而两个内项与两个外项是不变的， 2.4 和 40 仍然是外项， 1.6 和 60 仍然是内项。 分数形式 ： 探究新知 指出下面比例的外项和内项． 4.5∶2.7 = 10 ∶6 6 ∶10 = 9 ∶15 ∶ = 6 ∶4 外项 外项 内项 内项 外项 内项 2 6 16 48 = 外项 外项 内项 内项 巩固练习 2.4 ︰ 1.6 60 ︰ 40 ＝ 外项 内项 内项积是： 1.6 × 60 ＝ 96 外项积是： 2.4 × 40 ＝ 96 2.4 40 1.6 60 × × ＝ 计算下面比例中两个外项的积和两个内项的积。比较一下， 你能发现什么？ 探究新知 两个外项的积等于两个内项的积。 2.4 ︰ 1.6 60 ︰ 40 ＝ 2.4 1.6 ＝ 60 40 外项 外项 内项 内项 交叉相乘 ＝ 2.4 × 40 1.6 × 60 探究新知 3 5 ＝ 9 15 外项 外项 内项 内项 交叉相乘 ＝ 3 × 15 5 × 9 探究新知 6∶3 和 8∶5 3∶2 和 0.6∶0.4 2 80 5 200 和 验证 不能组成比例 3∶2=0.6∶0.4 2 80 5 200 = 能组成比例 写比例，验证发现! 在比例里，两个外项的积等于两个内项的积，这叫做比例的基本性质。 应用比例的基本性质，判断下面哪组中的两个比 可以组成比例． 1 、 6∶7 和 4∶5 2 、 0.2∶2.5 和 4∶50 因为： 6 × 5 ＝ 30 7 × 4 ＝ 28 所以： 6∶7 和 4∶5 不能组成比例． 因为： 0.2 × 50 ＝ 10 2.5 × 4 ＝ 10 所以： 能组成比例 0.2∶2.5 = 4∶50 30 28 ≠ 10 = 10 巩固练习 3 、 和 4 、 1.2: 和 比例 0:3=0:4 ，可以写成 3:0=4:0 吗？ 为什么？ 比例中两个比的后项都不能为 0 。 勤动脑 a : b ＝ c : d ＝ 或 ad ＝ bc ( b 、 d ≠0) 你能用字母表示比例的 基本性质吗？ 我能行 bc ＝ ad 应用比例的意义或者基本性质，判断下面哪组中 的两个比可以组成比例． 6∶9 和 9∶12 所以： 6∶9 和 9∶12 不能组成比例． 因为： 6 × 12 ＝ 72 9 × 9 ＝ 81 比例的意义： 因为： 6 ∶ 9 ＝ 9∶12 = 比例的基本性质： 所以： 6∶9 和 9∶12 不能组成比例． ≠ 72 ≠ 81 灵活应用 应用比例的意义或者基本性质，判断下面哪组中 的两个比可以组成比例 ． 1.4∶2 和 7∶10 因为： 1.4 ∶ 2 ＝ 0.7 所以： 1.4∶2 和 7∶10 可以组成比例． 1.4∶2 = 7∶10 因为： 1.4 × 10 ＝ 14 2 × 7 ＝ 14 比例的意义： 7∶10 = 0.7 比例的基本性质： 0.7 = 0.7 14 = 14 所以： 1.4∶2 和 7∶10 可以组成比例． 1.4∶2 = 7∶10 灵活应用 （ 1 ）在 a:7=9:b 中，（ ）是内项， （ ）是外项， a×b=( ) （ 2 ）一个比例的两个内项分别是 3 和 8 ， 则两个外项的积是（ ），两个外项可 能是（ ）和（ ）。 （ 3 ）在一个比例里，两个外项互为倒数， 那么两个内项的积是（ ），如果一个外项 是 ，另一个外项是（ ） 7 、 9 a 、 b 63 24 1 试一试 一、填空： 试一试 二、判断 1 、在比例中，两个外项的积减去两个内项的 积，差是 0 。 （ ） 2 、 18:30 和 3:5 可以组成比例。 （ ） 3 、如果 4:X=3:Y （ X 和 Y 均不为 0 ），那么 4X=3Y 。 （ ） 4 、因为 a×c=b×d ，所以 a:b=c:d （ ） 5 、 10 ： 2=5 是比例。 （ ） √ √ × × × 比例中等号的两侧必须都是一个比。 三、应用比例的基本性质 填空 1 、 6 : 3 = （ ） : 5 2 、 0.2 : 2.5 = 4 : ( ) 3 、 : ( ) = ： 4 、 = ( ) 8 10 50 1 6 10 5 、如果 5a=9b ，那么 a ： b=( ) ： ( ) 9 5 试一试 将下面的等式改写成比例，你能写出几组比例？ 3×40=8×15 把 3 和 40 当做外项 3: 8=15 :40 3: 15=8 :40 40: 8=15 :3 40: 15=8 :3 把 3 和 40 当做内项 8: 3=40 :15 8: 40=3 :15 15: 3=40 :8 15: 40=3 :8