- 136.03 KB
- 2022-02-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第03讲
图形的面积(上)
教学目标:
1、进行基本图形面积的求解,并可以综合运用;
2、学员在纸上画一画,并求出所画图形的面积;
3、培养学员的空间图性感,数字美感和灵活思维意识。
教学重点:
利用公式法、类比法、割补法、旋转平移法巧求周长和面积。
教学难点:
灵活选择合适的方法进行面积和周长计算。
教学过程:
【环节一:预习讨论,案例分析】
【知识回顾——温故知新】(参考时间-2分钟)
1、统计图:
统计图是把统计资料的数据用直观的方式呈现出来的一种形式。
统计图一般是根据整理好的统计表用点、线或立体图像等鲜明地表达统计量或其变化动态。
2、折线统计图:折线统计图用来表示数量增减变化的情况。
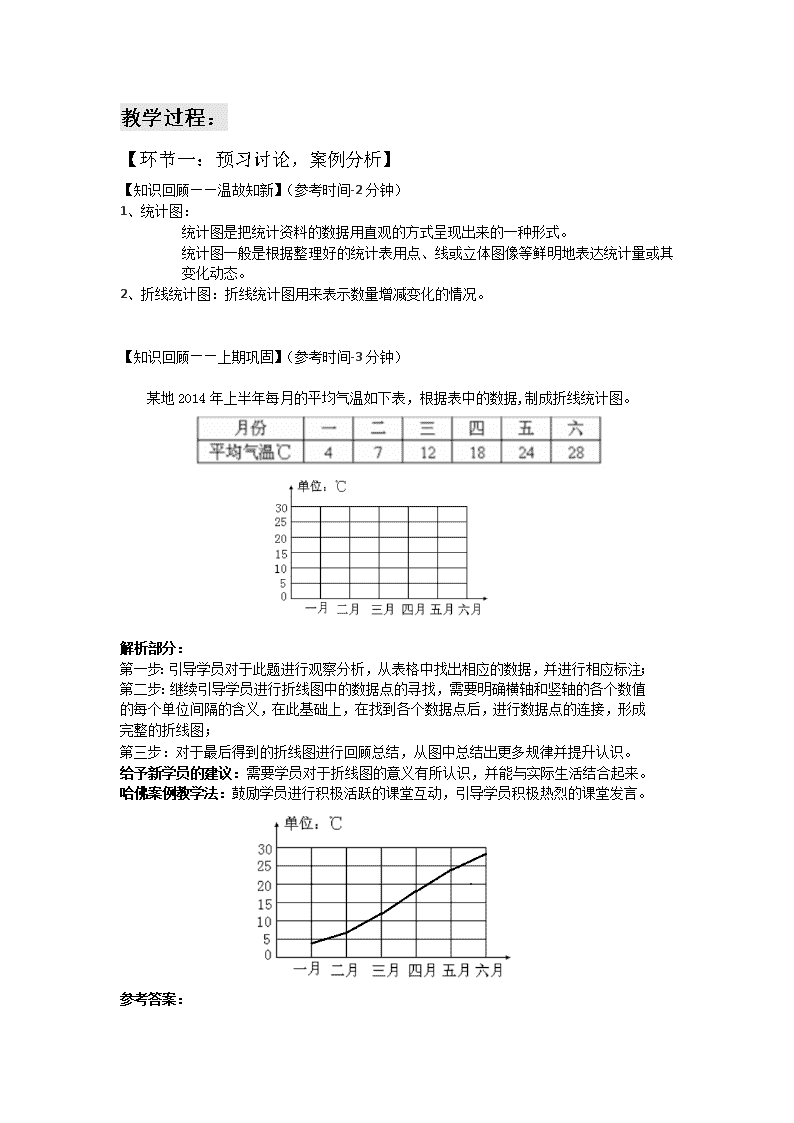
【知识回顾——上期巩固】(参考时间-3分钟)
某地2014年上半年每月的平均气温如下表,根据表中的数据,制成折线统计图。
解析部分:
第一步:引导学员对于此题进行观察分析,从表格中找出相应的数据,并进行相应标注;
第二步:继续引导学员进行折线图中的数据点的寻找,需要明确横轴和竖轴的各个数值的每个单位间隔的含义,在此基础上,在找到各个数据点后,进行数据点的连接,形成完整的折线图;
第三步:对于最后得到的折线图进行回顾总结,从图中总结出更多规律并提升认识。
给予新学员的建议:需要学员对于折线图的意义有所认识,并能与实际生活结合起来。
哈佛案例教学法:鼓励学员进行积极活跃的课堂互动,引导学员积极热烈的课堂发言。
参考答案:
【预习题分析——本期预习】(参考时间-7分钟)
手工课开始了,袋鼠老师将一张手工纸按照如图的折痕剪成4块,已知其中3块面积分别为2平方厘米,4平方厘米,6平方厘米,同学们你们知道第4块的面积有多大吗?
解析部分:
第一步:引导学员对于此题的图形进行观察分析,初步产生一个概略的认识和理解;
第二步:继续引导学员进行相关问题的具体解决分析,可以有“面积为2和面积为4的宽相同,则其面积之比就是长之比,即1:2,下部的两个长方形也拥有相同的宽,则其面积之比也是长度之比,亦1:2,故此,空白部分长方形的面积应该是6×2=12”;
第三步:最后对于此题的解题过程进行相应的分析,让学员有自己一定的认识和总结。
给予新学员的建议:此题需要学员通过代数过程帮助进行问题的解决,强调计算准确率。
哈佛案例教学法:鼓励学员积极参与小组内的讨论,并对此题有自己的思考判断和观点。
参考答案:
6×(4÷2)=12(平方厘米)
答:第4块的面积是12平方厘米。
【环节二:知识拓展、能力提升】
【知识点分析——本期知识点】(参考时间-2分钟)
一、求面积的方法一般有:
1、 运用公式法;
2、 图形转化法。
二、解题时要注意几点:
1、 贴着题意走,充分利用题目中给的每一个条件,题目没有图形时一定要画出示意图;
2、 当题目做不下去时,应当挖掘题目中的隐含条件或创造新条件;
3、可以添加辅助线或运用割补、转化、平移、分解、合并等方法,使不规则的图形转化为已学过的基本图形来求解。
同时,利用直接求或间接求的方法,根据问题确定要求什么,必须先求什么。
【例题分析——讲解室】(参考时间-10分钟)
如下图所示,一个长方形被分割成几个部分,请问带“?”部分的长方形面积是多少呢?
Ø 所给的图形可以分成多少块呢?
Ø 这个图形能不能通过分割转化为我们熟悉的图形?
解析部分:
第一步:引导学员对于此题中的图形进行观察分析,并且有一个概略的认识和把握;
第二步:继续引导学员对于图形进行观察和分析,可以有“上面给出了两个三角形的面积,对应的所在长方形的面积分别应该是26和14,然后观察右部的长方形,右上的面积和右下的面积之比是14:35即2:5,左部的长方形面积面积之比也应是2:5,即可求出左下部长方形的面积应该为60”;
第三步:最后根据所求的图形面积,对于整题进行回顾回忆,让学员有自己有一定认识。
给予新学员的建议:此题需要学员对于图形进行面积换比,并对于相应的图形进行分析。
哈佛案例教学法:鼓励学员进行积极活跃的课堂发言,调动起整个课堂的学习氛围和气氛。
参考答案:
7×2=14 12×2×(35÷14)=24×5÷2=60
答:带“?”部分的长方形面积是60。
【环节三:阶段复习】
【游戏环节——游乐场】(参考时间-2分钟)
游戏名称:数黑点
游戏规则:
参考答案: 略。
【练习分析——练习场(一)】(参考时间-7分钟)
迷你猫将手工纸沿着对边平行的方向剪成了9块,只知道3块的面积为6、9、12,请问同学们能不能请求出带“?”的这块的大小呢?
Ø 没有公共边,如何将面积关系转换到边长的关系?
Ø 如何利用边长的关系求“?”图形的面积?
解析部分:
第一步:引导学员对此图形进行观察,与之前题目进行对比,产生与前题的联想与联系;
第二步:继续引导学员进行此题的解决,可以有“右部的长方形的宽相同,所以面积之比就是长之比,与之相同的,左部的长方形的宽相同,面积之比也就是长之比,可知长之比是9:12即3:4,则左部的面积之比也是3:4,可以推断出?的面积等于8”;
第三步:最后引导学员对于此题进行回顾分析,从结果出发有更为深入的认识理解。
给予新学员的建议:需要学员对于图形进行认真的观察,并明确各部分的特征和联系。
哈佛案例教学法:鼓励学员进行热烈的小组内讨论,并对于自己的思考和观点进行积极发言。
参考答案:
6×(12÷9)=6×12÷9=8
答:带“?”的这块长方形的面积应为8。
【练习分析——练习场(二)】(参考时间-7分钟)
袋鼠老师将甲乙丙3张正方形的手工纸叠放在一起,它们的边长分别是6、8、10厘米,乙的一个顶点在甲的中心上,丙的一个顶点在乙的中心上,袋鼠老师问同学们:“你们知道三个正方形的覆盖面积是多少平方厘米吗?”
Ø 正方形重叠在一起,覆盖的总面积是否等于三个正方形的面积和?
Ø 如何将不规则的图形切拼成熟悉的图形?
解析部分:
第一步:引导学员对于图形进行观察分析,并鼓励学员在纸上对于此图形在纸上画一画;
第二步:继续引导学员进行具体的图形的处理和解决,可以有“先分析两个正方形重叠部分的面积,发现将图形进行切拼,阴影部分的两个三角形的面积相同,所以重叠部分的面积就等于一个小正方形的面积,又因为乙的顶点在甲的中心点,所以小正方形的面积为甲正方形面积的,同理可得乙、丙重叠部分的面积为乙正方形的”
第三步:最后引导学员进行解题过程的回顾分析,鼓励学员有自己的认识和理解。
给予新学员的建议:学员需要对于图形中具体数字意义有所理解,并进行图形分割补形。
哈佛案例教学法:引导学员对于此题的解决过程进行实际的纸上操作,带动热烈的课堂氛围。
参考答案:
(平方厘米)
答:三个正方形的覆盖面积是175平方厘米。
【本节总结】
一、求面积的方法一般有:
1、 运用公式法; 2、图形转化法。
二、解题时要注意几点:
1、贴着题意走,充分利用题目中给的每一个条件,题目没有图形时一定要画出示意图;
2、当题目做不下去时,应当挖掘题目中的隐含条件或创造新条件;
3、可以添加辅助线或运用割补、转化、平移、分解、合并等方法,使不规则的图形转化为已学过的基本图形来求解。
同时,利用直接求或间接求的方法,根据问题确定要求什么,必须先求什么。