北师大版数学六年级下册 《图形的放大与缩小》一课一练 (3) 8页

‎ ‎ 六年级下册数学一课一练-2.4图形的放大与缩小 ‎ 一、单选题 ‎ ‎1.一个直角三角形的两条直角边缩小到原来的 后，其斜边（  ）   ‎ A. 扩大3倍                          B. 不变                          C. 缩小到原来的                           D. 无法判断 ‎2.一块长方形操场，长与宽的比是5∶4，如果把这块操场按某种比例尺画在一张图纸上，那么在这张图纸上这块操场的长和宽的比是（   ） ‎ A. 5∶4                                    B. 4∶5                                    C. 3∶5                                    D. 5∶3‎ ‎3.一个长4cm，宽2cm的长方形按4：1放大，得到的图形的面积是（  ）cm2 ． ‎ A. 32                                           B. 72                                           C. 128‎ ‎4.如图所示的长方形按4：1缩小，所得的新长方形与原长方形的面积比是(   )。‎ A. 4：1                                   B. 1：4                                   C. 1：16                                   D. 16：1‎ ‎5.右面的图形是按一定的比例缩小的，x是（  ） ‎ A. 10                                          B. 8                                          C. 7.5                                          D. 6‎ 二、判断题 ‎ ‎6.一个图形放大或缩小后，大小改变，形状不变。 ‎ ‎7.把一个正方形按3：1放大，它的面积扩大到原来的3倍。 ‎ ‎8.把三角形的三条边都扩大3倍，它的高也扩大3倍． ‎ ‎9.把图形按一定比例放大后得到的图形与原图相比，大小不同，但形状相同。 ‎ 三、填空题 ‎ ‎ ‎ ‎ ‎ ‎10.一个半径是2cm的圆，按3：1的半径比放大，得到的圆的周长是________cm，面积是________cm2。 ‎ ‎11.如下图，将△EDC放大一定比例成△ABC，直角△DCE的三条边分别是3cm、4cm、5cm。如果AB=6cm，那么AE=________cm。 ‎ ‎ ‎ ‎12.把正方形按5：1的比放大，放大后图形的边长是原来正方形边长的________倍，面积是原来正方形面积的________倍。 ‎ ‎13.一个长8cm、宽5cm的长方形按5：1的比例放大后，得到的图形的面积是________。 ‎ ‎14.把一个长方形按1∶4的比例缩小，缩小后长方形与原来长方形的周长比是________． ‎ 四、解答题 ‎ ‎15.下面作图是图形A按1：2缩小后的得到的图形，请你在右面的格子里画出原图。   ‎ ‎16.                  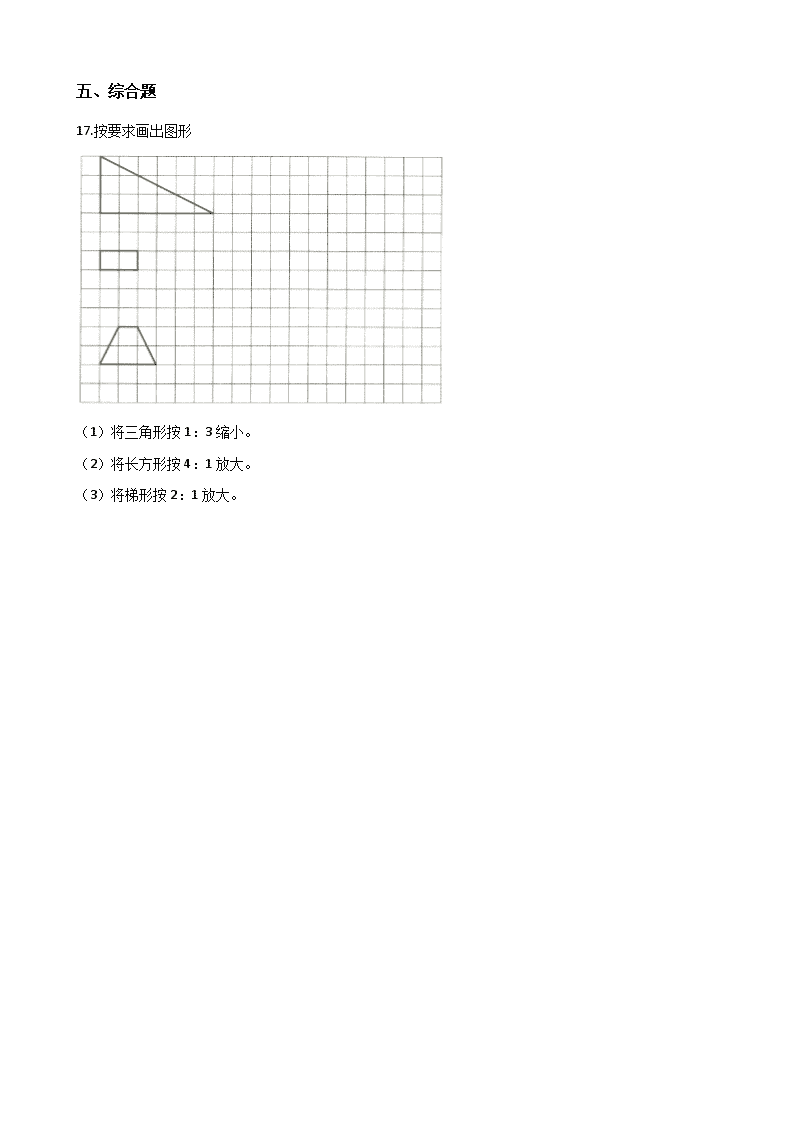‎ ‎（1）画出三角形ABC绕B点逆时针旋转90°后的图形 ‎（2）在方格纸上按2：1画出如图中圆形放大后的图形 ‎ ‎（3）原有圆形与放大后圆形面积的最简比是________ ‎ ‎ ‎ ‎ ‎ 五、综合题 ‎ ‎17.按要求画出图形 ‎（1）将三角形按1：3缩小。 ‎ ‎（2）将长方形按4：1放大。 ‎ ‎（3）将梯形按2：1放大。 ‎ ‎ ‎ ‎ ‎ 参考答案 一、单选题 ‎1.【答案】 C ‎ ‎【解析】解答：一个直角三角形的两条直角边缩小到原来的 后，其斜边缩小到原来的 。分析：此题考查放缩，对应放大或缩小。‎ ‎2.【答案】 A ‎ ‎【解析】【解答】放大或缩小后长方形的长和宽的比是不变的，所以图纸上操场的长和宽的比是5:4. 故答案为：A ‎【分析】图形的放大后缩小，只改变图形的大小，不改变图形的形状，图形各部分的比例是不变的.‎ ‎3.【答案】C ‎ ‎【解析】【解答】放大后的长：4×4=16（厘米）；‎ 放大后的宽：2×4=8（厘米）；‎ 面积：16×8=128（平方厘米）；‎ ‎【分析】先根据按4：1放大，放大后长和宽是原来的4倍，求出放大后的长和宽，再求出面积。‎ 故答案选：C ‎4.【答案】 C ‎ ‎【解析】【解答】解：24÷4=6(cm)，20÷4=5(cm)，新长方形与原长方形的面积比是：(6×5)：(24×20)=30：480=1：16 故答案为：C ‎【分析】把原来的长方形的长和宽都除以4求出缩小后的长与宽，然后写出两个长方形的面积比并化成最简整数比即可.‎ ‎5.【答案】C ‎ ‎【解析】【解答】x：5=12：8‎ ‎8 x =5×12‎ x =7.5‎ 答：x是7.5；‎ ‎【分析】根据对应的长与宽的比是12：8，由此列出比例式，解答即可。‎ 故选：C ‎ ‎ ‎ ‎ 二、判断题 ‎6.【答案】 正确 ‎ ‎【解析】【解答】解：一个图形放大或缩小后，大小改变，形状不变。 故答案为：正确。 【分析】将一个图形放大或缩小，是按照比例放大或缩小，所以形状不会变，而大小会改变。‎ ‎7.【答案】错误 ‎ ‎【解析】【解答】把一个正方形按3：1的比例放大后，周长扩大到原来的3倍．而面积要扩大到原来的9倍． 故答案为：错误． 【分析】本题考点：图形的放大与缩小． 此题主要考查正方形的周长及面积公式． 依据正方形的面积公式可知，边长扩大3倍，则其面积应扩大9倍，从而能判断正误．‎ ‎8.【答案】正确 ‎ ‎【解析】【解答】解：三条边都扩大3倍，三角形的高也扩大3倍，原题说法正确.故答案为：正确 【分析】三角形的三条边都扩大3倍，那么这个三角形就是按照3:1的比放大，三角形的高也扩大相同的倍数.‎ ‎9.【答案】正确 ‎ ‎【解析】【解答】解：图形按一定的比例放大或缩小后与原图相比，大小不同，形状相同，原题说法正确. 故答案为：正确【分析】图形放大或缩小就是把图形的每条边的长度都扩大或缩小相同的倍数，大小不同，形状相同.‎ 三、填空题 ‎10.【答案】37.68；113.04 ‎ ‎【解析】【解答】解：2×3=6(cm)，周长：3.14×6×2=37.68(cm)，面积：3.14×6²=113.04(cm²) 故答案为：37.68；113.04【分析】用原来的半径乘3即可求出放大后的半径长度.圆周长：C=2πr，圆面积：S=πr²，根据周长和面积公式计算即可.‎ ‎11.【答案】 5 ‎ ‎【解析】【解答】6÷3=2， 5×2-5 =10-5 =5（cm）.‎ ‎ ‎ ‎ ‎ ‎ 故答案为：5. 【分析】观察图可知，△EDC中的直角边ED=3cm，放大后变成了AB，AB=6cm，则放大的比例是6：3=2：1；则放大后斜边AC的长度是：5×2=10cm，AE=AC-EC=10-5=5cm，据此解答.  ‎ ‎12.【答案】5；25 ‎ ‎【解析】【解答】解：按5:1放大后，边长是原来的5倍，面积扩大为原来的52=25倍. 故答案为：5；25【分析】正方形面积=边长×边长，按5：1放大就是把边长扩大5倍，则面积就扩大边长扩大的倍数的平方倍.‎ ‎13.【答案】1000平方厘米 ‎ ‎【解析】【解答】解：8×5=40(厘米)，5×5=25(厘米)，面积：40×25=1000(平方厘米) 故答案为：1000平方厘米【分析】用长方形的长和宽分别乘5求出放大后的长和宽，用放大后的长乘宽即可求出得到图形的面积.‎ ‎14.【答案】1∶4 ‎ ‎【解析】【解答】按1：4的比例缩小，原来的图形就是缩小后图形长度的4倍，那么缩小后长方形与原来长方形的周长比是1：4. 故答案为：1：4 【分析】根据长方形的周长公式可知，缩小后的图形的长度之比与周长之比是相同的，由此直接判断即可.‎ 四、解答题 ‎15.【答案】解：如图所示：   ‎ ‎【解析】【分析】按照1:2的比缩小图形，就是把原图形的每条边的长度都缩小到原来的2倍，因此根据左图中各边的格数确定缩小后图形各边的格数再画出图形即可.‎ ‎16.【答案】 （1）解：如图所示：‎ ‎ ‎ ‎ ‎ ‎（2）解：如图所示：‎ ‎（3）1:4 ‎ ‎【解析】【分析】(1)先确定旋转中心，再确定旋转方向，然后根据旋转度数确定对应点的位置后画出图形即可；(2)先确定放大后圆的半径是4格，然后画出放大后的圆；(3)圆的半径扩大了2倍，那么面积就扩大4倍，由此写出原来的图形与放大后的圆形面积的比.‎ 五、综合题 ‎17.【答案】 （1）解：如图： ‎ ‎ ‎ ‎ ‎ ‎（2）解：如图： （3）解：如图： ‎ ‎【解析】【分析】(1)缩小后的三角形的两条直角边分别是1格、2格；(2)放大后的长方形的长是8格，宽是4格；(3)放大后的梯形上底是2格，下底是6格，高是4格.‎ ‎ ‎