人教版数学六年级下册总复习3空间与图形立体图形 36页

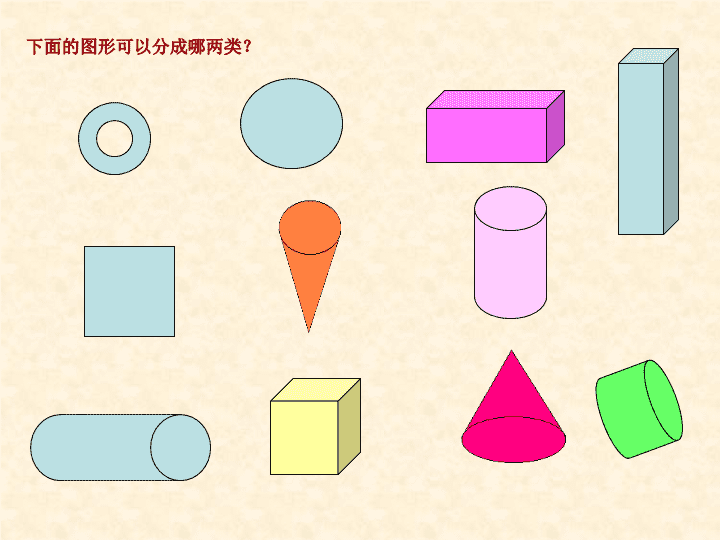
小 学 数 学 总 复 习 人教版六年级数学下册第六单元 空间与图形 三、立体图形的认识 下面的图形可以分成哪两类？ 立体图形 长方体 正方体 圆锥体 圆柱体 球 . .o 立体图形 长方体 正方体 圆锥体 圆柱体 球 ( 特殊的长方体） 立体图形 长方体 正方体 圆锥体 圆柱体 球 都是 平面 围成的 有 曲面 棱长 面积 面的形状 点 棱 面 正方体 长方体 关系 不同点 相同点 形体 8 个 6 个 12 条 6 个面一般都是长方形 （也有可能有两个相对的面是正方形） 相对的面的面积相等 每一组互相平行的 四条棱长度相等 6 个面都是相等的正方形 6 个面的面积都相等 12 条棱的长度都相等 正方体是 特殊 的长方体 棱长和 = （长 + 宽 + 高 ) × 4 圆柱圆锥有什么特点？ 圆锥 圆柱 高 侧面 底面 o h o r o h r 图 形 展开是个 扇形 一个圆 两底之间的距离（ 无数条 ） 展开是一 长方形或正方形 两个完全相同的圆 顶点到底面之间的距离（ 一条 ） 1 、有两个底面： 2 、一个侧面： 面积相等 宽 长 高 长 = 底面周长 圆柱的特征： 扇形 侧面展开 底面 圆形 h 从圆锥的顶点到底面圆心的距离 叫做圆锥的高。 圆锥的特征 ： 长方体 长 宽 高 棱长 棱长 棱长 半径 高 圆柱 正方体 长 × 宽 棱长 × 棱长 （长 × 宽 + 长 × 高 + 宽 × 高 × 2 棱长 × 棱长 × 6 侧面积 +2 个底面积 半径 高 底面积 表面积 长方体 长 宽 高 圆柱 正方体 图形名称 π× 半径 2 图形名称 沿着一条高剪开的 平面图形 立体图形 长方体 正方体 圆锥体 圆柱体 球 长方体的表面积 = 前、后 + 左、右 + 上、下 正方体的表面积 = 每个面的面积 ×6 圆柱的侧面积 = 底面周长 × 高 圆柱的表面积 = 侧面积 + 底面积 ×2 练一练 1 ： 1 、填空 1 、把圆柱的侧面沿高展开，一般可以得到 （ 形），这个图形的长相当于（ ），宽相当于（ ）。 2 、用一根铁丝焊接成一个长 10 厘米、宽 3 厘米、高 2 厘米的长方体框架，至少需要铁丝（ ）厘米。 3 、一个长方体最多可以有（ ）个面是正方形。 长方 圆柱的底面周长 圆柱的高 2 、判断题 （ 1 ）长方体和正方体都有六个面，而且六个面都相等。 … ………………………………………… （ ）（ 2 ）圆锥体的高有一条；圆柱体的高有两条。 ……………………………………………… （ ）（ 3 ）圆柱的侧面展开后是一个正方形，那么它的底面周长和高一定相等。 …………………………… （ ） （ 4 ）正方体的棱长总和是 48 厘米，它的每条棱长是 8 厘米。 ……………………………………………… （ ） （ 5 ）圆柱体的体积等于圆锥体的 3 倍。 …… （ ） （ 6 ）一个正方体的棱长是 6 厘米，它的表面积和体积相等。 ……………………………………………… （ ） （ 7 ）容器的容积与容器的体积大小不一样 。（ ） × × × × × √ √ 3 、填空 （ 1 ）做一个圆柱形铁皮罐头盒，求需要多少铁皮，是求它的（ ），罐头盒周围贴商标纸， 求商标纸的面积是求它的（ ） 。 （ 2 ） 做一只圆柱形通风管要用多少铁皮，是求它的 （ ）。 （ 3 ） 下雨时 , 给打谷场上的圆锥形谷堆盖上塑料防雨布 , 所需防雨布的最小面积是指圆锥的 ( ) 。 表面积 侧面积 侧面积 侧面积 转化 实验、转化 推导体积计算公式 推导体积计算公式 立体图形体积计算 长方体 正方体 圆锥体 圆柱体 球 长方体的体积 = 长 × 宽 × 高 正方体的体积 = 棱长 × 棱长 × 棱长 圆柱的体积 = 底面积 × 高 圆锥体积 = × 底面积 × 高 长方体、 正方体、 圆柱体的体积 = 底面积 × 高 a b h a a a s h V=abh V=sh s 3 V=a V=sh V=sh o r V= sh V=sh 应用练习： 1 、计算下列立体图形的表面积和体积； 10 5 4 5 5 5 2 10 单位：厘米 一、填空； 1 、一个 正方体的底面周长是 4 分米，它的表面积是（ ），体积是 （ ）。 2 、一个圆柱和圆锥的体积相等，底面积也相等。圆柱和圆锥的高的比是（ ） 二、答一答 1. 把长方体横截成两个长方体 , 表面积增加几个面 ? 2. 把长方体纵剖成两面个长方体 , 表面积增加几个面 ? 3. 把几个正方体拼成一个长方体 , 表面积发生什么变化 ? 4. 把 横剖 , 纵剖 ( 沿底面积直径 ) 表面 积怎么变 ? 1 . 一个长方体木箱，长是 60cm ，宽是 50cm ，高是 40cm ，这个木箱的占地面积是多少？表面积是多少？ 2 . 一对无 盖的长方体木盒长 40cm ，宽 35cm ，高 30cm ，把它的外面涂上红漆，涂漆的面积是多？ 3. 李师傅要制 40 根长方体通风管，管口是边长为 20 的正方形，管长 1 ，一共需要多少平方米的铁皮？ 4. 学校微机室铺了 1800 块长 40cm, 宽 20cm, 厚 1cm 的地砖 , 这个微机室的面积是多少平方米 ? 1. 把一根长 3m ，底面直径 2 dm 的圆柱形钢管截 3 段，表面积增加了多少 ? 思考题 ？ 下课了， 再见！