小学数学精讲教案4_3_3 任意四边形、梯形与相似模型（一） 学生版 5页

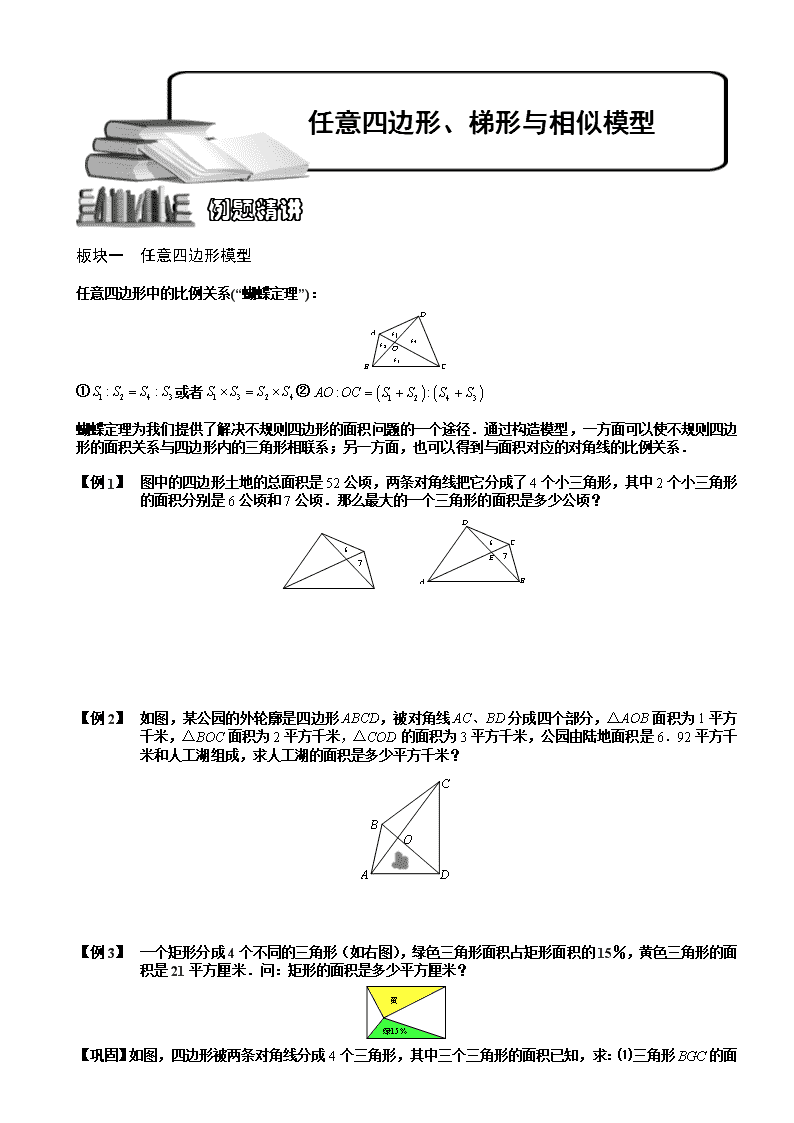
任意四边形、梯形与相似模型 例题精讲 板块一 任意四边形模型 任意四边形中的比例关系(“蝴蝶定理”)：‎ ‎①或者②‎ 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．‎ 【例 1】 图中的四边形土地的总面积是‎52公顷，两条对角线把它分成了4个小三角形，其中2个小三角形的面积分别是‎6公顷和‎7公顷．那么最大的一个三角形的面积是多少公顷？‎ ‎ ‎ 【例 2】 如图，某公园的外轮廓是四边形ABCD，被对角线AC、BD分成四个部分，△AOB面积为1平方千米，△BOC面积为2平方千米，△COD的面积为3平方千米，公园由陆地面积是6．92平方千米和人工湖组成，求人工湖的面积是多少平方千米？‎ 【例 3】 一个矩形分成4个不同的三角形（如右图），绿色三角形面积占矩形面积的15％，黄色三角形的面积是21平方厘米．问：矩形的面积是多少平方厘米？‎ ‎【巩固】如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知，求：⑴三角形 的面积；⑵？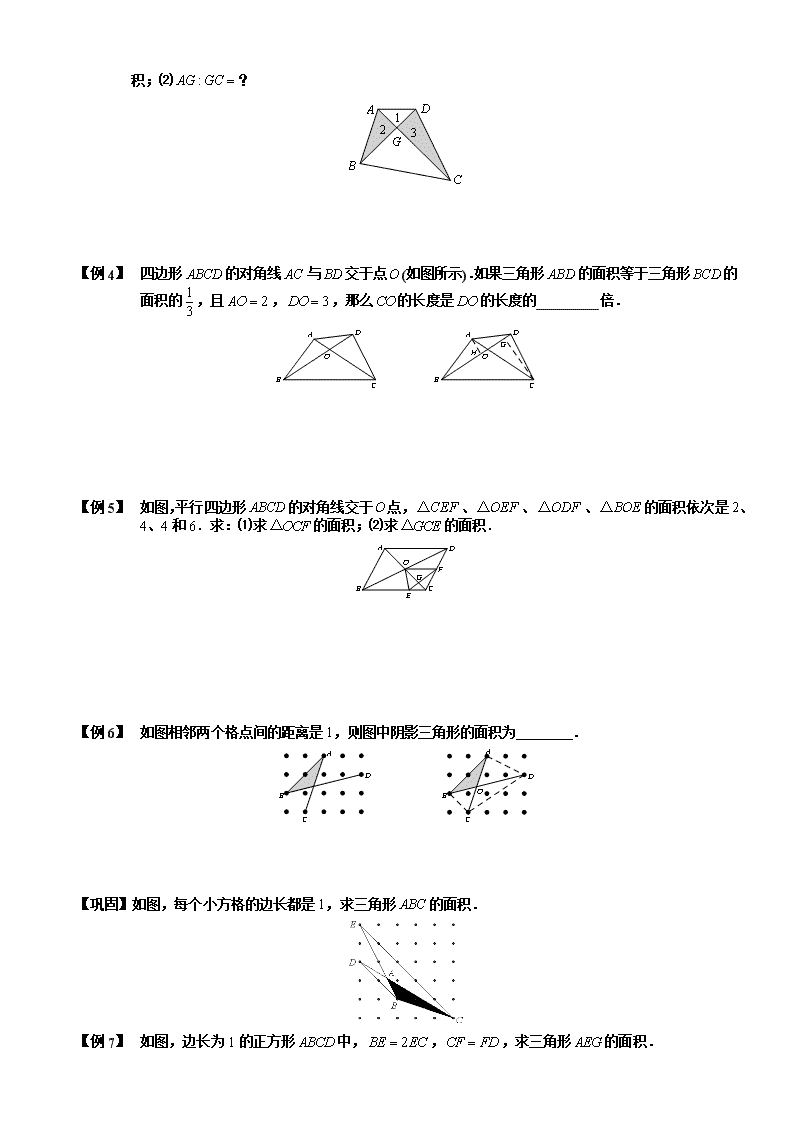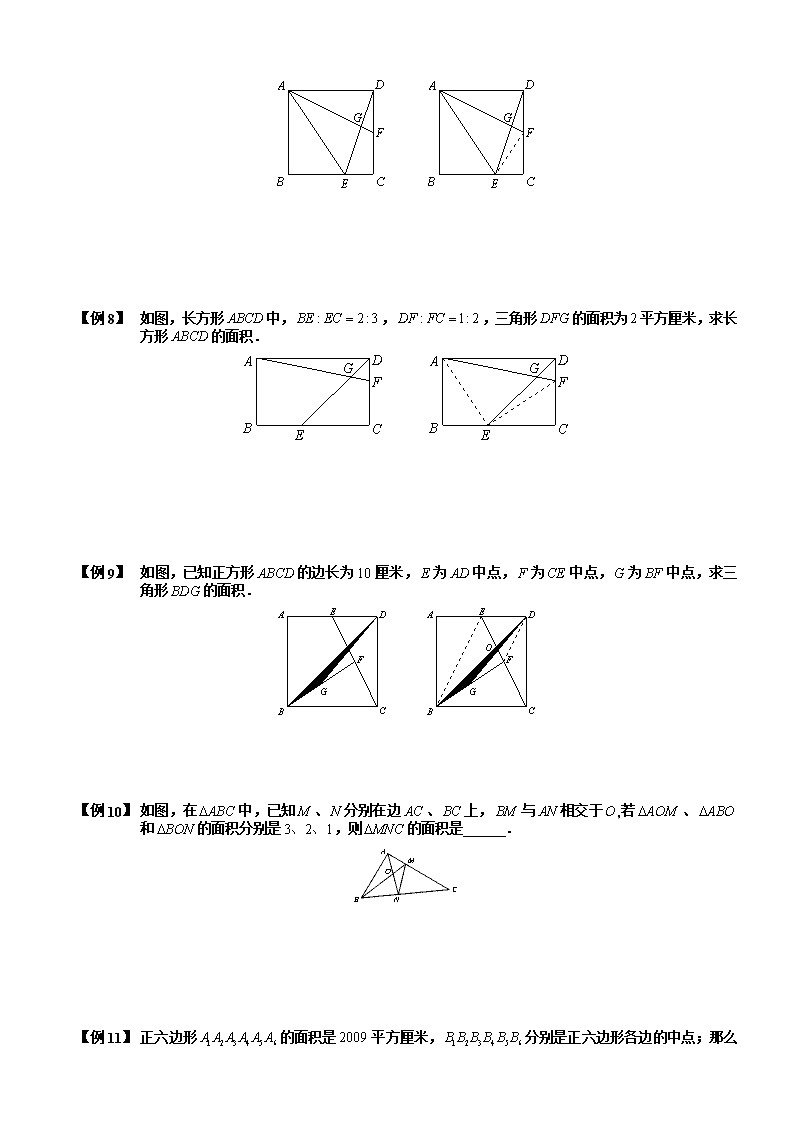‎ 【例 1】 四边形的对角线与交于点(如图所示)．如果三角形的面积等于三角形的面积的，且，，那么的长度是的长度的_________倍．‎ ‎ ‎ 【例 2】 如图，平行四边形的对角线交于点，、、、的面积依次是2、4、4和6．求：⑴求的面积；⑵求的面积．‎ 【例 3】 如图相邻两个格点间的距离是1，则图中阴影三角形的面积为 ．‎ ‎ ‎ ‎【巩固】如图，每个小方格的边长都是1，求三角形的面积．‎ 【例 4】 如图，边长为1的正方形中，，，求三角形的面积．‎ ‎ ‎ 【例 1】 如图，长方形中，，，三角形的面积为平方厘米，求长方形的面积．‎ ‎ ‎ 【例 2】 如图，已知正方形的边长为‎10厘米，为中点，为中点，为中点，求三角形的面积．‎ ‎ ‎ 【例 3】 如图，在中，已知、分别在边、上，与相交于,若、和的面积分别是3、2、1，则的面积是 ．‎ 【例 4】 正六边形的面积是2009平方厘米，‎ 分别是正六边形各边的中点；那么图中阴影六边形的面积是 平方厘米．‎ ‎ ‎ 【例 1】 如图，ABCD是一个四边形，M、N分别是AB、CD的中点．如果△ASM、△MTB与△DSN的面积分别是6、7和8，且图中所有三角形的面积均为整数，则四边形ABCD的面积为 ．‎ ‎ ‎ 【例 2】 已知是平行四边形，，三角形的面积为平方厘米。则阴影部分的面积是 平方厘米。‎ 【例 3】 正方形ABCD边长为‎6厘米，AE＝AC，CF＝BC。三角形DEF的面积为 平方厘米。‎ 【例 4】 如图4，在三角形ABC中，已知三角形ADE、三角形DCE、三角形BCD的面积分别是89、28、26，那么三角形DBE的面积是 。‎