六年级奥数教案：第19周 面积计算 6页

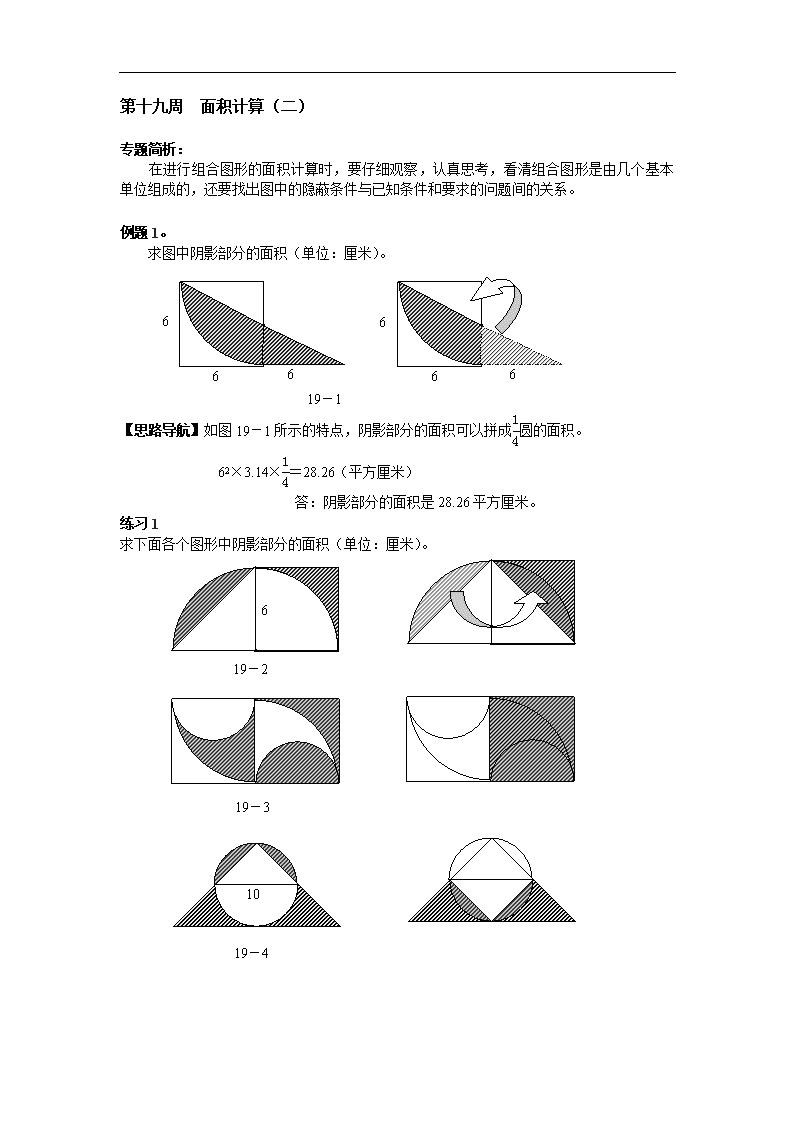
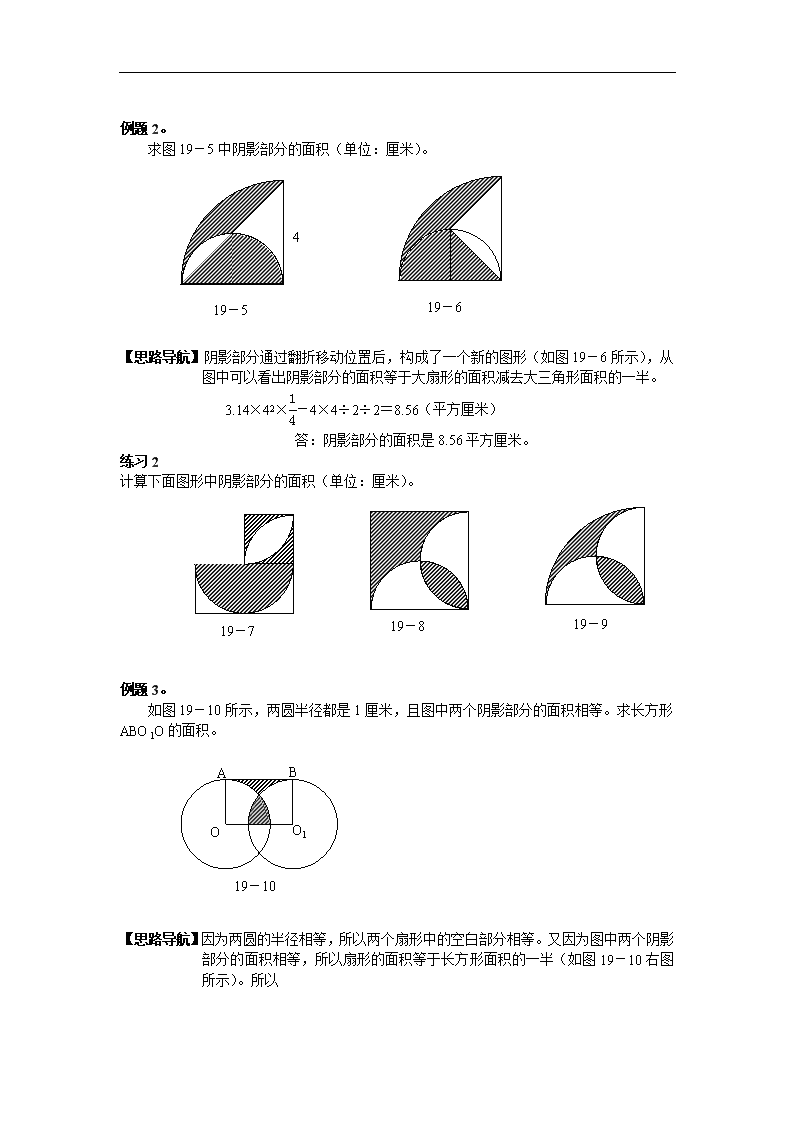
第十九周 面积计算（二）‎ 专题简析：‎ 在进行组合图形的面积计算时，要仔细观察，认真思考，看清组合图形是由几个基本单位组成的，还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。‎ 例题1。‎ 求图中阴影部分的面积（单位：厘米）。‎ ‎6‎ ‎6‎ ‎6‎ ‎6‎ ‎6‎ ‎6‎ ‎19－1‎ ‎【思路导航】如图19－1所示的特点，阴影部分的面积可以拼成圆的面积。‎ ‎ 62×3.14×＝28.26（平方厘米）‎ ‎ 答：阴影部分的面积是28.26平方厘米。‎ 练习1‎ 求下面各个图形中阴影部分的面积（单位：厘米）。‎ ‎6‎ ‎6‎ ‎19－2‎ ‎19－3‎ ‎10‎ ‎19－4‎ 例题2。‎ 求图19－5中阴影部分的面积（单位：厘米）。‎ ‎4‎ ‎19－6‎ ‎19－5‎ ‎【思路导航】阴影部分通过翻折移动位置后，构成了一个新的图形（如图19－6所示），从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。‎ ‎ 3.14×42×－4×4÷2÷2＝8.56（平方厘米）‎ ‎ 答：阴影部分的面积是8.56平方厘米。‎ 练习2‎ 计算下面图形中阴影部分的面积（单位：厘米）。‎ ‎19－8‎ ‎19－9‎ ‎19－7‎ 例题3。‎ 如图19－10所示，两圆半径都是‎1厘米，且图中两个阴影部分的面积相等。求长方形ABO1O的面积。‎ B A O O1‎ ‎19－10‎ ‎【思路导航】因为两圆的半径相等，所以两个扇形中的空白部分相等。又因为图中两个阴影部分的面积相等，所以扇形的面积等于长方形面积的一半（如图19－10右图所示）。所以 ‎ 3.14×12××2＝1.57（平方厘米）‎ ‎ 答：长方形长方形ABO1O的面积是1.57平方厘米。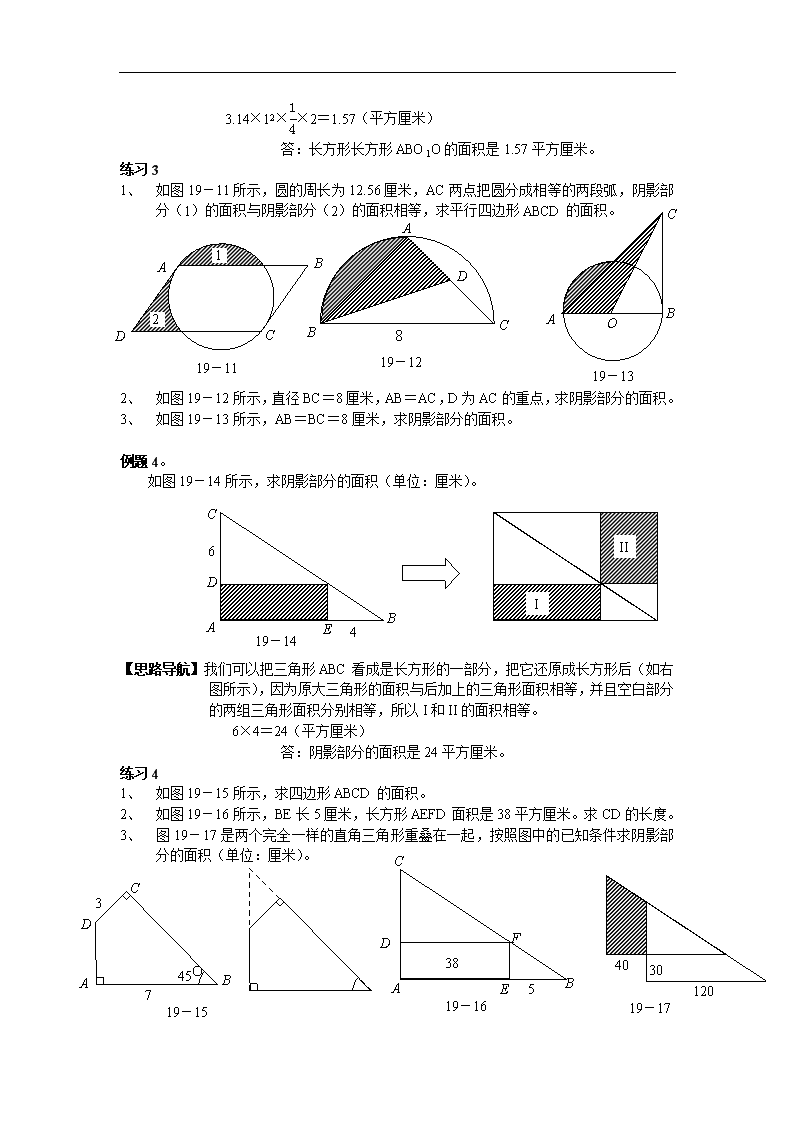‎ 练习3‎ C A C B D ‎8‎ 1、 如图19－11所示，圆的周长为‎12.56厘米，AC两点把圆分成相等的两段弧，阴影部分（1）的面积与阴影部分（2）的面积相等，求平行四边形ABCD的面积。‎ D A C B ‎1‎ ‎2‎ B A O ‎19－13‎ ‎19－12‎ ‎19－11‎ 2、 如图19－12所示，直径BC＝‎8厘米，AB＝AC，D为AC的重点，求阴影部分的面积。‎ 3、 如图19－13所示，AB＝BC＝‎8厘米，求阴影部分的面积。‎ 例题4。‎ 如图19－14所示，求阴影部分的面积（单位：厘米）。‎ C II ‎6B D I EB B A ‎4B ‎19－14‎ ‎【思路导航】我们可以把三角形ABC看成是长方形的一部分，把它还原成长方形后（如右图所示），因为原大三角形的面积与后加上的三角形面积相等，并且空白部分的两组三角形面积分别相等，所以I和II的面积相等。‎ ‎ 6×4＝24（平方厘米）‎ ‎ 答：阴影部分的面积是24平方厘米。‎ 练习4‎ 1、 如图19－15所示，求四边形ABCD的面积。‎ 2、 如图19－16所示，BE长‎5厘米，长方形AEFD面积是38平方厘米。求CD的长度。‎ C 3、 图19－17是两个完全一样的直角三角形重叠在一起，按照图中的已知条件求阴影部分的面积（单位：厘米）。‎ C ‎3‎ B A ‎45○‎ ‎7‎ F D D ‎38‎ B ‎40‎ ‎30‎ ‎5‎ E A ‎120‎ ‎19－16‎ ‎19－15‎ ‎19－17‎ 例题5。‎ 如图19－18所示，图中圆的直径AB是‎4厘米，平行四边形ABCD的面积是7平方厘米，∠ABC＝30度，求阴影部分的面积（得数保留两位小数）。‎ C O B A D D C O B A ‎19－18‎ ‎【思路导航】阴影部分的面积等于平行四边形的面积减去扇形AOC的面积，再减去三角形BOC的面积。‎ ‎ 半径：4÷2＝2（厘米）‎ ‎ 扇形的圆心角：180－（180－30×2）＝60（度）‎ ‎ 扇形的面积：2×2×3.14×≈2.09（平方厘米）‎ ‎ 三角形BOC的面积：7÷2÷2＝1.75（平方厘米）‎ ‎ 7－（2.09+1.75）＝3.16（平方厘米）‎ ‎ 答：阴影部分的面积是3.16平方厘米。‎ 练习5‎ 1、 如图19－19所示，∠1＝15度，圆的周长位‎62.8厘米，平行四边形的面积为100平方厘米。求阴影部分的面积（得数保留两位小数）。‎ 2、 如图19－20所示，三角形ABC的面积是31.2平方厘米，圆的直径AC＝‎6厘米，BD：DC＝3：1。求阴影部分的面积。‎ 3、 如图19－21所示，求阴影部分的面积（单位：厘米。得数保留两位小数）。‎ O A B D C C A ‎5.2‎ ‎30○‎ ‎60○‎ B O ‎12‎ B A ‎19－21‎ ‎19－20‎ ‎19－19‎ ‎5.2‎ C B A D C ‎26‎ ‎30○‎ ‎30○‎ ‎12‎ B A ‎60‎ ‎30○‎ D C B A ‎26‎ ‎60‎ 答案：‎ 练1‎ 1、 图答19－1阴影部分的面积为：6×6×＝18平方厘米 2、 图答19－2阴影部分的面积为：6×6＝36平方厘米 3、 图答19－3阴影部分的面积为：10×（10÷2）××2＝50平方厘米 练2‎ 1、 图答19－4中阴影部分的面积为：（2+2）×2＝8平方厘米 2、 图答－5阴影部分的面积为：4×4×＝8平方厘米 3、 图答19－6阴影部分的面积为：42×3.14×－4×4×＝4.56平方厘米 练3‎ 1、 图答19－7中，阴影部分（1）的面积与阴影部分（2）的面积相等。所以，平行四边形的面积和圆的面积相等。因此，平行四边形ABCD的面积是：‎ ‎（12.56÷3.14÷2）2×3.14＝12.56平方厘米 ‎2、 （8÷2）2×3.14×＝12.56平方厘米 ‎3、 （8÷2）2×3.14×+（8÷2）×＝20.56平方厘米 ‎ 第二题和第三题，阴影部分的面积通过等积变形后可知。如图答19－7和图答19－8所示。‎ 练4‎ 1、 如图答19－9所示：延长BC和AD相距与E，四边形ABCD的面积是：‎ ‎7×7×－3×3×＝20平方厘米 2、 如图答19－10所示，因为S1＝S2，所以CD＝38÷5＝‎‎7.6厘米 3、 如图答19－11所示：阴影部分面积等于梯形的面积，其面积为：（120+120－40）×30÷2＝3000平方厘米 练5‎ 1、 如图答19－12所示 圆心角AOB的度数为180－（180－15×2）＝30度 平行四边形内一个小弓形的面积为 ‎（62.8÷3.14÷2）2×3.14×－100÷4＝1.17平方厘米 ‎ 阴影部分的面积为100÷2－1.17＝48.83平方厘米 2、 如图答19－13所示：圆心角AOD的度数为180－（180－60×2）＝120度 扇形AOD的面积为（6÷2）2×3.14×＝9.42平方厘米 阴影部分的面积为9.42－31.2××＝5.52平方厘米 3、 如图答19－14（1）所示：‎ 圆心角AOC的度数为180－30×2＝120度 扇形AOC的面积（12÷2）2×3.14×＝37.68平方厘米 三角形AOC的面积为（12÷2）×5.2×＝15.6平方厘米 阴影部分的面积37.68－15.6＝22.08平方厘米 如图答19－14（2）所示 圆心角BOC的读书180－（180－30×2）＝60度 扇形ABD的面积602×3.14×＝942平方厘米 三角形AOC的面积（60÷2）×26×＝390平方厘米 扇形BOC的面积（60÷2）×3.14×＝471平方厘米 阴影部分的面积942－390－471＝81平方厘米