中考总复习一次函数专题 13页

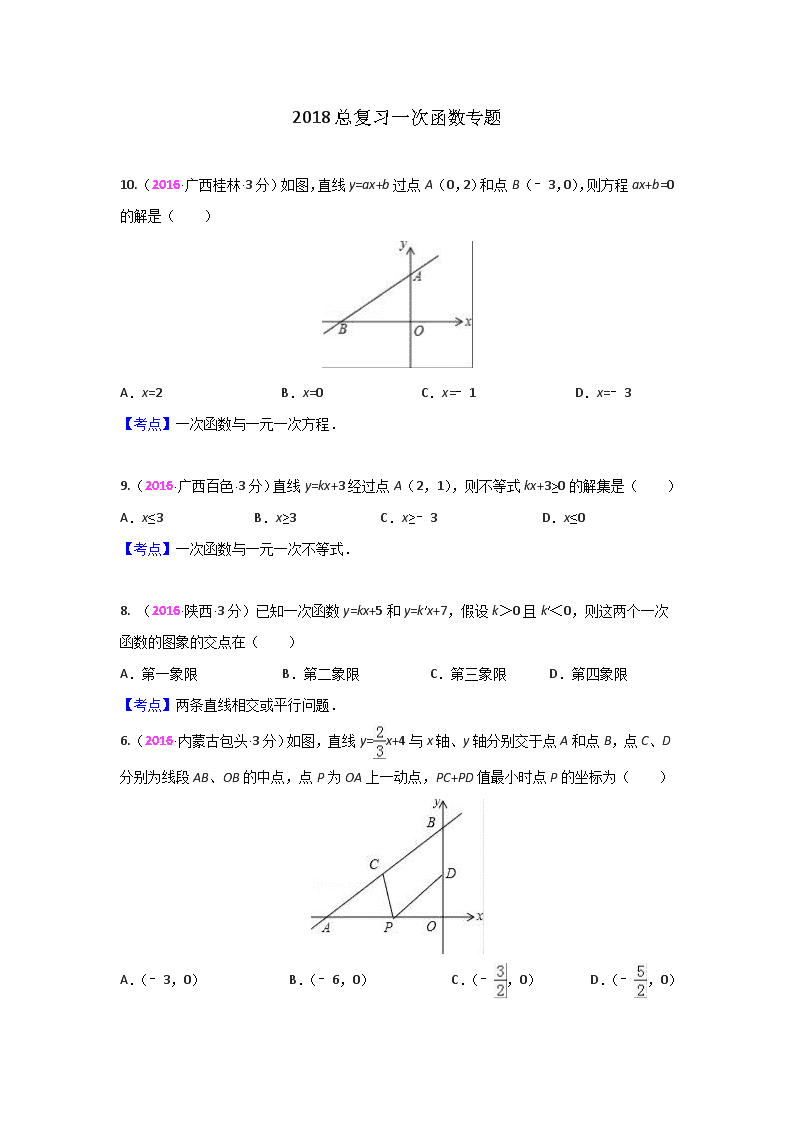
‎2018总复习一次函数专题 ‎10.（2016·广西桂林·3分）如图，直线y=ax+b过点A（0，2）和点B（﹣3，0），则方程ax+b=0的解是（　　）‎ A．x=2 B．x=0 C．x=﹣1 D．x=﹣3‎ ‎【考点】一次函数与一元一次方程．‎ ‎9.（2016·广西百色·3分）直线y=kx+3经过点A（2，1），则不等式kx+3≥0的解集是（　　）‎ A．x≤3 B．x≥3 C．x≥﹣3 D．x≤0‎ ‎【考点】一次函数与一元一次不等式．‎ ‎8. 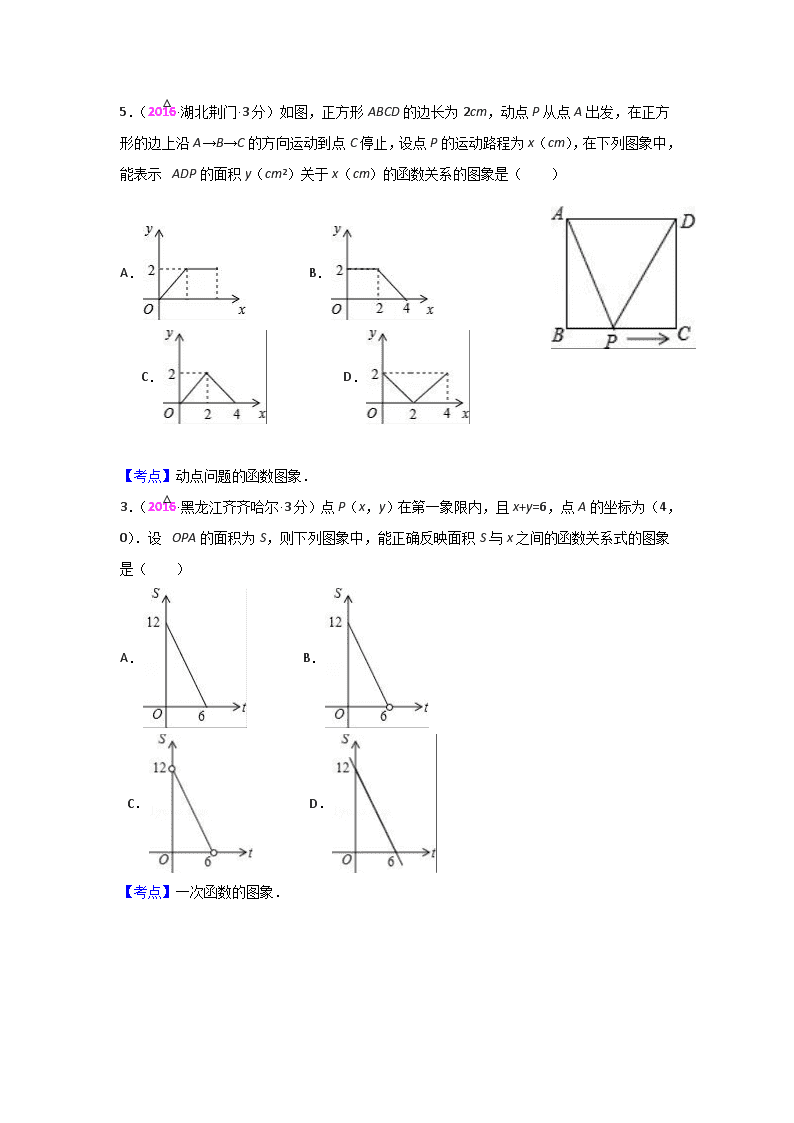（2016·陕西·3分）已知一次函数y=kx+5和y=k′x+7，假设k＞0且k′＜0，则这两个一次函数的图象的交点在（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【考点】两条直线相交或平行问题．‎ ‎6.（2016·内蒙古包头·3分）如图，直线y=x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（　　）‎ A．（﹣3，0） B．（﹣6，0） C．（﹣，0） D．（﹣，0）‎ ‎5．（2016·湖北荆门·3分）如图，正方形ABCD的边长为2cm，动点P从点A出发，在正方形的边上沿A→B→C的方向运动到点C停止，设点P的运动路程为x（cm），在下列图象中，能表示△ADP的面积y（cm2）关于x（cm）的函数关系的图象是（　　）‎ A． B． ‎ ‎ C． D．‎ ‎【考点】动点问题的函数图象．‎ ‎3．（2016·黑龙江齐齐哈尔·3分）点P（x，y）在第一象限内，且x+y=6，点A的坐标为（4，0）．设△OPA的面积为S，则下列图象中，能正确反映面积S与x之间的函数关系式的图象是（　　）‎ A． B． ‎ ‎ C． D．‎ ‎【考点】一次函数的图象．‎ ‎1. （2016·四川宜宾）如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（　　）‎ A．乙前4秒行驶的路程为48米 B．在0到8秒内甲的速度每秒增加4米/秒 C．两车到第3秒时行驶的路程相等 D．在4至8秒内甲的速度都大于乙的速度 ‎【考点】函数的图象．‎ ‎1. （2016·湖北武汉·3分）将函数y＝2x＋b（b为常数）的图象位于x轴下方的部分沿x轴翻折至其上方后，所得的折线是函数y＝|2x＋b|（b为常数）的图象．若该图象在直线y＝2下方的点的横坐标x满足0＜x＜3，则b的取值范围为_________．‎ ‎【考点】一次函数图形与几何变换 ‎【答案】-4≤b≤-2‎ ‎【解析】根据题意：列出不等式 ，解得-4≤b≤-2‎ ‎4．（2016·湖北荆州·3分）若点M（k﹣1，k+1）关于y轴的对称点在第四象限内，则一次函数y=（k﹣1）x+k的图象不经过第　一　象限．‎ ‎5.（2016·山东潍坊·3分）在平面直角坐标系中，直线l：y=x﹣1与x轴交于点A1，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点Bn的坐标是　（2n﹣1，2n﹣1）　．‎ ‎6. （2016·四川眉山·3分）若函数y=（m﹣1）x|m|是正比例函数，则该函数的图象经过第　二、四　象限 ‎7.（2016·山东省东营市·4分）如图，直线y＝x＋b与直线y＝kx＋6交于点P(3，5)，则关于x的不等式x＋b＞kx＋6的解集是_____________．‎ ‎【知识点】一次函数——一次函数与一元一次不等式 ‎9. （2016·重庆市A卷·4分）甲、乙两人在直线道路上同起点、同终点、同方向，分别以不同的速度匀速跑步1500米，先到终点的人原地休息，已知甲先出发30秒后，乙才出发，在跑步的整个过程中，甲、乙两人的距离y（米）与甲出发的时间x（秒）之间的关系如图所示，则乙到终点时，甲距终点的距离是　175　米． ‎ ‎【分析】根据图象先求出甲、乙的速度，再求出乙到达终点时所用的时间，然后求出乙到达终点时甲所走的路程，最后用总路程﹣甲所走的路程即可得出答案． ‎ ‎【解答】解：根据题意得，甲的速度为：75÷30=2.5米/秒， ‎ 设乙的速度为m米/秒，则（m﹣2.5）×150=75， ‎ 解得：m=3米/秒， ‎ 则乙的速度为3米/秒， ‎ 乙到终点时所用的时间为： =500（秒）， ‎ 此时甲走的路程是：2.5×（500+30）=1325（米）， ‎ 甲距终点的距离是1500﹣1325=175（米）． ‎ 故答案为：175． ‎ ‎【点评】本题考查了一次函数的应用，读懂题目信息，理解并得到乙先到达终点，然后求出甲、乙两人所用的时间是解题的关键．‎ ‎10. （2016·重庆市B卷·4分）为增强学生体质，某中学在体育课中加强了学生的长跑训练．在一次女子800米耐力测试中，小静和小茜在校园内200米的环形跑道上同时起跑，同时到达终点；所跑的路程S（米）与所用的时间t（秒）之间的函数图象如图所示，则她们第一次相遇的时间是起跑后的第　120　秒．‎ ‎【考点】一次函数的应用．‎ ‎【分析】分别求出OA、BC的解析式，然后联立方程，解方程就可以求出第一次相遇时间．‎ ‎【解答】解：设直线OA的解析式为y=kx，‎ 代入A（200，800）得800=200k，‎ 解得k=4，‎ 故直线OA的解析式为y=4x，‎ 设BC的解析式为y1=k1x+b，由题意，得，‎ 解得：，‎ ‎∴BC的解析式为y1=2x+240，‎ 当y=y1时，4x=2x+240，‎ 解得：x=120．‎ 则她们第一次相遇的时间是起跑后的第120秒．‎ 故答案为120．‎ ‎【点评】本题考查了一次函数的运用，一次函数的图象的意义的运用，待定系数法求一次函数的解析式的运用，解答时认真分析求出一次函数图象的数据意义是关键．‎ ‎2. （2016·吉林·8分）甲、乙两人利用不同的交通工具，沿同一路线从A地出发前往B地，甲出发1h后，y甲、y乙与x之间的函数图象如图所示．‎ ‎（1）甲的速度是　60　km/h；‎ ‎（2）当1≤x≤5时，求y乙关于x的函数解析式；‎ ‎（3）当乙与A地相距240km时，甲与A地相距　220　km．‎ ‎【考点】一次函数的应用．‎ ‎【分析】（1）根据图象确定出甲的路程与时间，即可求出速度；‎ ‎（2）利用待定系数法确定出y乙关于x的函数解析式即可；‎ ‎（3）求出乙距A地240km时的时间，乘以甲的速度即可得到结果．‎ ‎【解答】解：（1）根据图象得：360÷6=60km/h；‎ ‎（2）当1≤x≤5时，设y乙=kx+b，‎ 把（1，0）与（5，360）代入得：，‎ 解得：k=90，b=﹣90，‎ 则y乙=90x﹣90；‎ ‎（3）令y乙=240，得到x=，‎ 则甲与A地相距60×=220km，‎ 故答案为：（1）60；（3）220‎ ‎3. （2016·江西·6分）如图，过点A（2，0）的两条直线l1，l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB=．‎ ‎（1）求点B的坐标；‎ ‎（2）若△ABC的面积为4，求直线l2的解析式．‎ ‎【考点】两条直线相交或平行问题；待定系数法求一次函数解析式；勾股定理的应用．‎ ‎【分析】（1）先根据勾股定理求得BO的长，再写出点B的坐标；‎ ‎（2）先根据△ABC的面积为4，求得CO的长，再根据点A、C的坐标，运用待定系数法求得直线l2的解析式．‎ ‎【解答】解：（1）∵点A（2，0），AB=‎ ‎∴BO===3‎ ‎∴点B的坐标为（0，3）；‎ ‎（2）∵△ABC的面积为4‎ ‎∴×BC×AO=4‎ ‎∴×BC×2=4，即BC=4‎ ‎∵BO=3‎ ‎∴CO=4﹣3=1‎ ‎∴C（0，﹣1）‎ 设l2的解析式为y=kx+b，则 ‎，解得 ‎∴l2的解析式为y=x﹣1‎ ‎8．(2016·孝感)孝感市在创建国家级园林城市中，绿化档次不断提升．某校计划购进A，B两种树木共100棵进行校园绿化升级．经市场调查：购买A种树木2棵，B种树木5棵，共需600元；购买A种树木3棵，B种树木1棵，共需380元．‎ ‎(1)求A种、B种树木每棵各多少元；‎ ‎(2)因布局需要，购买A种树木的数量不少于B种树木数量的3倍．学校与中标公司签订的合同中规定：在市场价格不变的情况下(不考虑其他因素)，实际付款总金额按市场价九折优惠．请设计一种购买树木的方案，使实际所花费用最少，并求出最少的费用．‎ 解：(1)设A种、B种树木每棵分别为a元、b元，则 解得 答：A种、B种树木每棵分别为100元、80元．‎ ‎(2)设购买A种树木为x棵，则购买B种树木为(100－x)棵，‎ 则x≥3(100－x)，解得x≥75.‎ 设实际付款总金额为y元，则 y＝0.9[100x＋80(100－x)]＝18x＋7 200.‎ ‎∵18>0，∴y随x的增大而增大．‎ ‎∴x＝75时，y最小．‎ 即x＝75，y最小＝18×75＋7 200＝8 550.‎ ‎∴当购买A种树木75棵，B种树木25棵时，所需费用最少，最少费用为8 550元．‎ ‎7．(2016·泰安)某学校是乒乓球体育传统项目学校，为进一步推动该项目的开展，学校准备到体育用品店购买直拍球拍和横拍球拍若干副，并且每买一副球拍必须要买10个乒乓球，乒乓球的单价为2元/个，若购买20副直拍球拍和15副横拍球拍花费9 000元；购买10副横拍球拍比购买5副直拍球拍多花费1 600元．‎ ‎(1)求两种球拍每副各多少元；‎ ‎(2)若学校购买两种球拍共40副，且直拍球拍的数量不多于横拍球拍数量的3倍，请你给出一种费用最少的方案，并求出该方案所需费用．‎ 解：(1)设直拍球拍每副x元，横拍球拍每副y元，由题意，得 解得 答：直拍球拍每副220元，横拍球拍每副260元．‎ ‎(2)设购买直拍球拍m副，则购买横拍球拍(40－m)副，由题意，得 m≤3(40－m)．解得m≤30.‎ 设买40副球拍所需的费用为w元，则 w＝(220＋2×10)m＋(260＋2×10)(40－m)‎ ‎＝－40m＋11 200.‎ ‎∵－40＜0，∴w随m的增大而减小．‎ ‎∴当m＝30时，w取最小值，w最小＝－40×30＋11 200＝10 000(元)．‎ 答：购买直拍球拍30副，购买横拍球拍10副时，费用最少，最少为10 000元．‎ ‎1．(2016·德州)下列函数中，满足y的值随x的值增大而增大的是( B )‎ A．y＝－2x B．y＝3x－1 C．y＝ D．y＝x2‎ ‎2．(2015·眉山)关于一次函数y＝2x－1的图象，下列说法正确的是( B )‎ A．图象经过第一、二、三象限 B．图象经过第一、三、四象限 C．图象经过第一、二、四象限 D．图象经过第二、三、四象限 ‎3．(2015·宁德)已知点A(－2，y1)和点B(1，y2)是如图所示的一次函数y＝2x＋b图象上的两点，则y1与y2的大小关系是( A )‎ A．y1＜y2 B．y1＞y2 C．y1＝y2 D．y1≥y2‎ ‎4．(2016·陕西)设点A(a，b)是正比例函数y＝－x的图象上任意一点，则下列等式一定成立的是( D )‎ A．2b＋3b＝0 B．2a－3b＝0‎ C．3a－2b＝0 D．3a＋2b＝0‎ ‎5．(2016·河北)若k≠0，b<0，则y＝kx＋b的图象可能是( B )‎ ‎6．(2016·呼和浩特)已知一次函数y＝kx＋b－x的图象与x轴的正半轴相交，且函数值y随自变量x的增大而增大，则k，b的取值情况为( A )‎ A．k＞1，b＜0 B．k＞1，b＞0‎ C．k＞0，b＞0 D．k＞0，b＜0‎ ‎7．(2016·宜宾)如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是( C )‎ A．乙前4秒行驶的路程为48米 B．在0到8秒内甲的速度每秒增加4米/秒 C．两车到第3秒时行驶的路程相等 D．在4至8秒内甲的速度都大于乙的速度 ‎8．(2016·钦州)已知正比例函数y＝kx的图象经过点(1，2)，则k＝2．‎ ‎9．将正比例函数y＝2x的图象向上平移3个单位，所得直线的解析式为y＝2x＋3．‎ ‎10．(2014·毕节)如图，函数y＝2x和y＝ax＋4的图象相交于点A(m，3)，则不等式2x≥ax＋4的解集为x≥．‎ ‎11．(2016·荆州)若点M(k－1，k＋1)关于y轴的对称点在第四象限内，则一次函数y＝(k－1)x＋k的图象不经过第一象限．‎ ‎12．(2016·长春)如图，在平面直角坐标系中，正方形ABCD的对称中心与原点重合，顶点A的坐标为(－1，1)，顶点B在第一象限．若点B在直线y＝kx＋3上，则k的值为－2．‎ ‎13．(2016·宜昌)如图，直线y＝x＋与两坐标轴分别交于A，B两点．‎ ‎(1)求∠ABO的度数；‎ ‎(2)过点A的直线l交x轴正半轴于C，AB＝AC，求直线l的函数解析式．‎ 解：(1)对于y＝x＋，令x＝0，则y＝.‎ ‎∴A点的坐标为(0，)，‎ ‎∴OA＝.‎ 令y＝0，则x＝－1，∴OB＝1.‎ 在Rt△AOB中，tan∠ABO＝＝.‎ ‎∴∠ABO＝60°.‎ ‎(2)在△ABC中，AB＝AC，又AO⊥BC，‎ ‎∴BO＝CO，‎ ‎∴C点的坐标为(1，0)．‎ 设直线l的函数解析式为y＝kx＋b(k，b为常数)，‎ 依题意，有解得 ‎∴直线l的函数解析式为y＝－x＋.‎ ‎14．(2013·河池)华联超市欲购进A，B两种品牌的书包共400个．已知两种书包的进价和售价如下表所示．设购进A种书包x个，且所购进的两种书包能全部卖出，获得的总利润为w元．‎ 品牌 进价(元/个)‎ 售价(元/个)‎ A ‎47‎ ‎65‎ B ‎37‎ ‎50‎ ‎(1)求w关于x的函数关系式；‎ ‎(2)如果购进两种书包的总费用不超过18 000元，那么该商场如何进货才能获利最大？并求出最大利润．(提示：利润＝售价－进价)‎ 解：(1)由题意，得 w＝(65－47)x＋(50－37)(400－x)‎ ‎＝5x＋5 200.‎ ‎∴w关于x的函数关系式为w＝5x＋5 200.‎ ‎(2)由题意，得 ‎47x＋37(400－x)≤18 000，解得x≤320.‎ ‎∵w＝5x＋5 200，∴k＝5＞0，‎ ‎∴w随x的增大而增大．‎ ‎∴当x＝320时，w最大＝6 800.‎ ‎∴进货方案是A种书包购买320个，B种书包购买80个，才能获得最大利润，最大利润为6 800元．‎ ‎15．(2016·新疆)暑假期间，小刚一家乘车去离家380公里的某景区旅游，他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示．‎ ‎(1)从小刚家到该景区乘车一共用了多少时间？‎ ‎(2)求线段AB对应的函数解析式；‎ ‎(3)小刚一家出发2.5小时时离目的地多远？‎ 解：(1)从小刚家到该景区乘车一共用了4 h.‎ ‎(2)设AB段图象的函数解析式为y＝kx＋b.‎ ‎∵A(1，80)，B(3，320)在AB上，‎ ‎∴解得 ‎∴y＝120x－40(1≤x≤3)．‎ ‎(3)当x＝2.5时，y＝120×2.5－40＝260，‎ ‎380－260＝120(km)．‎ 故小刚一家出发2.5小时时离目的地120 km.‎ ‎16．(2016·枣庄)如图，点A的坐标为(－4，0)，直线y＝x＋n与坐标轴交于点B，C，连接AC.若∠ACD＝90°，则n的值为－．‎ ‎　　‎ ‎17．(2016·重庆A卷)甲，乙两人在直线道路上同起点，同终点，同方向，分别以不同的速度匀速跑步1 500米，先到终点的人原地休息．已知甲先出发30秒后，乙才出发．在跑步的整个过程中，甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示．则乙到终点时，甲距终点的距离是175米．‎ ‎18．如图，已知A，B分别是x轴上位于原点左、右两侧的点，点P(2，p)在第一象限，直线PA交y轴于点C(0，2)，直线PB交y轴于点D，S△AOP＝6.‎ ‎(1)求△COP的面积；‎ ‎(2)求点A的坐标和p的值；‎ ‎(3)若S△BOP＝S△DOP，求直线BD的解析式．‎ 解：(1)作PE⊥y轴于点E，‎ ‎∵P点的横坐标是2，则PE＝2.‎ ‎∴S△COP＝OC·PE＝×2×2＝2.‎ ‎(2)∵S△AOC＝S△AOP－S△COP＝6－2＝4，‎ 又S△AOC＝OA·OC，‎ ‎∴×OA×2＝4.∴OA＝4.‎ ‎∴点A的坐标是(－4，0)．‎ 设直线AP的解析式是y＝kx＋b，则 解得 则直线AP的解析式是y＝x＋2.‎ 当x＝2时，y＝3，即p＝3.‎ ‎(3)设直线BD的解析式为y＝ax＋c(a≠0)，‎ ‎∴D(0，c)，B(－，0)．‎ ‎∵S△BOP＝S△DOP，‎ ‎∴OD·2＝OB·3，即c＝－.‎ ‎∵P(2，3)，∴2a＋c＝3.‎ ‎∴解得 ‎∴直线BD的解析式是y＝－x＋6.‎