中考数学猜想性专题目三轮冲刺 9页

‎2013中考总结复习冲刺练：猜想性专题 一、中考要求 能够根据题目中的图形或者数字直观地发现共同特征，或者发展变化的趋势，据此去预测估计它的规律或者其他相关结论，使带有猜想性质的推断尽可能与现实情况相吻合，必要时可以进行验证或者证明，依此体现出猜想的实际意义。‎ 二、知识网络图 如图1所示：‎ 猜想性问题 猜想规律型 猜想结论型 猜想数式规律 猜想图形规律 猜想数值结果 猜想数量关系 猜想变化情况 图1‎ 三、基础知识整理 猜想规律型的问题难度相对较小，经常以填空等形式出现，解题时要善于从所提供的数字或图形信息中，寻找其共同之处，这个存在于个例中的共性，就是规律。其中蕴含着“特殊——一般——特殊”的常用模式，体现了总结归纳的数学思想，这也正是人类认识新生事物的一般过程。‎ 相对而言，猜想结论型问题的难度较大些，具体题目往往是直观猜想与科学论证、具体应用的结合，解题的方法也更为灵活多样：计算、验证、类比、比较、测量、绘图、移动等等，都能用到。‎ 由于猜想本身就是一种重要的数学方法，也是人们探索发现新知的重要手段，非常有利于培养创造性思维能力，所以备受命题专家的青睐，逐步成为中考的又一热点。‎ 四、考点分析 ‎1、猜想数式规律 通常给定一些数字、代数式、等式或者不等式，然后猜想其中蕴含的规律。一般解法是先写出数式的基本结构，然后通过横比（比较同一等式中不同部分的数量关系）或纵比（比较不同等式间相同位置的数量关系）找出各部分的特征，改写成要求的格式。‎ 例1（云南）观察按下列顺序排列的等式：‎ ‎；‎ ‎；‎ ‎；‎ ‎；‎ ‎；‎ ‎ ……‎ 猜想：第个等式（为正整数）用表示，可以表示成________________.‎ 分析：根据以上各等式所呈现出来的特征，可以猜想这个等式的基本结构形式为 ‎9 × 一个数 + 另一个数 = 结果 其中，“另一个数”就是等式的序号n；“一个数”比它小1，即为n-1；结果的个位为1，个位以前的数字等于“一个数”n-1，所以结果表示为10(n-1)+1. 因此，这个等式为 ‎9(n-1) + n = 10(n-1) + 1.‎ 这个猜想的结果是否正确，还可以用整式运算的知识加以验证。‎ 等式的左边 = 9n - 9 + n = 10n – 9；等式的右边 = 10n – 10 + 1 = 10n – 9 .‎ 所以，等式的左边 = 等式的右边。‎ 说明所列等式成立。‎ ‎2、猜想图形规律 根据一组相关图形的变化规律，从中总结通过图形的变化所反映的规律。其中，以图形为载体的数字规律最为常见。猜想这种规律，需要把图形中的有关数量关系列式表达出来，再对所列式进行对照，仿照猜想数式规律的方法得到最终结论。‎ ‎……‎ ‎……‎ ‎①1=12；‎ ‎②1+3=22；‎ ‎③1+2+5=32；‎ ‎④ ；‎ ‎⑤ ；‎ 例2（河北课改实验区）观察图2所示的点阵图和相应的等式，探究其中的规律：‎ 图2‎ ‎（1）在④和⑤后面的横线上分别写出相应的等式；‎ ‎（2）通过猜想写出与第n个点阵相对应的等式.‎ 分析：（1）本题图形中所反映出来的数字关系已经列出三个，下面就以它们为例，填写后两个。易得④1+3+5+7=42；⑤1+3+5+7+9=52.‎ ‎（2）仿照例1的思路可以猜想：1+3+5+…+(2n-1)=n2 . ‎ ‎3、猜想数值结果 当在一些条件改变的前提下，结果的数值不变，或者其变化呈现出某种特征时，可以猜想在新条件下，数值仍然不变，或者仍然按照原来的特征变化，依此猜想到结果的数值。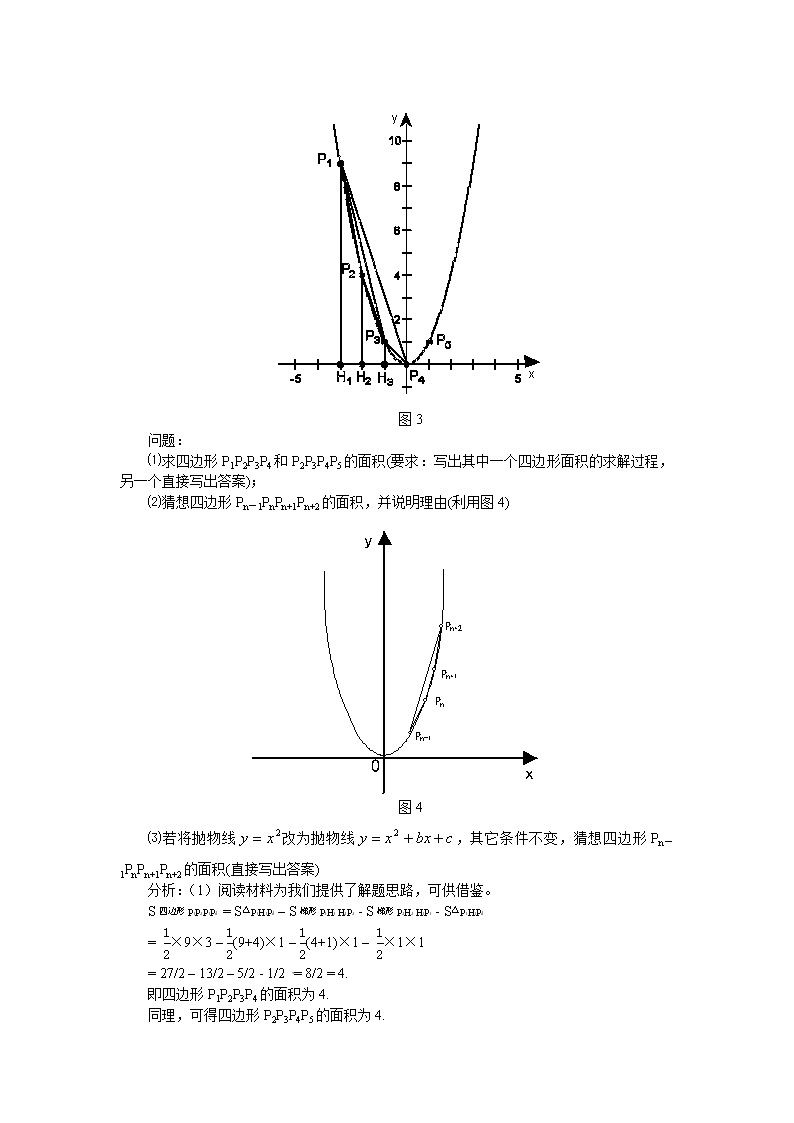‎ 例3（辽宁大连）阅读材料，解答问题。‎ 材料：“小聪设计的一个电子游戏是：一电子跳蚤从这P1(－3 ，9)开始，按点的横坐标依次增加1的规律，在抛物线上向右跳动，得到点P2、P3、P4、P5……(如图3所示)。过P1、P2、P3分别作P1H1、P2H2、P3H3垂直于x轴，垂足为H1、H2、H3，则 即△P1P2P3的面积为1。”‎ 图3‎ 问题：‎ ‎⑴求四边形P1P2P3P4和P2P3P4P5的面积(要求：写出其中一个四边形面积的求解过程，另一个直接写出答案)；‎ ‎⑵猜想四边形Pn－1PnPn+1Pn+2的面积，并说明理由(利用图4)‎ 图4‎ ‎⑶若将抛物线改为抛物线，其它条件不变，猜想四边形Pn－1PnPn+1Pn+2的面积(直接写出答案)‎ 分析：（1）阅读材料为我们提供了解题思路，可供借鉴。‎ S四边形P1P2P3P4 = S△P1H1P4 – S梯形P1H1 H2P2 - S梯形P2H2 H3P3 - S△P3H3P4‎ ‎= ×9×3 – (9+4)×1 – (4+1)×1 – ×1×1‎ ‎= 27/2 – 13/2 – 5/2 - 1/2 = 8/2 = 4.‎ 即四边形P1P2P3P4的面积为4.‎ 同理，可得四边形P2P3P4P5的面积为4.‎ ‎（2）猜想四边形Pn－1PnPn+1Pn+2的面积为4. 理由如下： ‎ 设点Pn－1、Pn、Pn+1、Pn+2的纵坐标分别为(x-1)2、x2、(x+1)2、(x+2)2，则 S四边形Pn－1PnPn+1Pn+2‎ ‎= S梯形Pn－1Hn-1Hn+2Pn+2 – S梯形Pn－1Hn-1HnPn - S梯形PnHnHn+1Pn+1 - S梯形Pn+1Hn+1Hn+2Pn+2‎ ‎= ×[(x-1)2+(x+2)2]×3 – [(x-1)2+ x2]×1 – [ x2+(x+1)2]×1 – ×[(x+1)2+(x+2)2]×1‎ ‎= (2x2+2x+5) – (2 x2-2x+1) – (2 x2+2x+1) – (2 x2+6x+5)‎ ‎= [(6x2+6x+15)- (2 x2-2x+1) –(2 x2+2x+1) –(2 x2+6x+5)]‎ ‎= 8/2 = 4.‎ 即四边形Pn－1PnPn+1Pn+2的面积为4.‎ ‎（3）由于抛物线改为抛物线后，如果其它条件不变，只是抛物线的位置发生了变化，它的形状以及四边形Pn－1PnPn+1Pn+2的形状都不变，所以猜想四边形Pn－1PnPn+1Pn+2的面积也不变，仍为4.‎ ‎4、猜想数量关系 数量关系的表现形式多种多样，这些关系不一定就是我们目前所学习的函数关系式。在猜想这种问题时，通常也是根据题目给出的关系式进行类比，仿照猜想数式规律的方法解答。‎ 例4（江苏连云港）（1）如图5，在梯形ABCD中，AB∥CD，，，E为AD边上的任意一点，EF∥AB，且EF交BC于点F，某学生在研究这一问题时，发现如下事实：‎ 图5‎ ‎①当时，有；‎ ‎②当时，有；‎ ‎③当时，有．‎ 当时，参照上述研究结论，请你猜想用k表示DE的一般结论，并给出证明；‎ 图6‎ ‎（2）现有一块直角梯形田地（如图6所示），其中AB∥CD，，‎310米，‎170米，‎‎70米 ‎．若要将这块地分割成两块，由两农户来承包，要求这两块地均为直角梯形，且它们的面积相等．请你给出具体分割方案．‎ 分析：猜想的东西未必完全正确，鉴于此，本题按照“猜想——证明——应用”的思路设计题目，体现了知识的产生过程、科学论证和应用价值。‎ ‎（1）仿照例1、例2的解题思路，不难猜想出关系式：EF =．‎ ‎ 证明：过点E作BC的平行线交AB于G，交CD的延长线于H．‎ ‎∵AB∥CD，∴∽，∴，‎ 又////，∴，‎ ‎∵，，‎ ‎∴，可得．‎ ‎（2）在上取一点E，作EF∥AB交BC于点F，设，‎ 则EF=，， ‎ 若，则，‎ ‎∵梯形ABCD、DCFE为直角梯形，‎ ‎∴， ‎ 化简得解得：，（舍去）， ‎ ‎∴，‎ 所以只需在AD上取点E，使米，作EF∥AB（或），‎ 即可将梯形分成两个直角梯形，且它们的面积相等． ‎ ‎5、猜想变化情况 随着数字或图形的变化，它原先的一些性质有的不会改变，有的则发生了变化，而且这种变化是有一定规律的。比如，在几何图形按特定要求变化后，只要本质不变，通常的规律是“位置关系不改变，乘除乘方不改变，减变加法加变减，正号负号要互换”。这种规律可以作为猜想的一个参考依据。‎ 例5（山东青岛）四边形是大家最熟悉的图形之一，我们已经发现了它的许多性质.只要善于观察、乐于探索，我们还会发现更多的结论.‎ ‎(1)四边形一条对角线上任意一点与另外两个顶点的连线，将四边形分成四个三角形(如图7)，其中相对的两对三角形的面积之积相等.你能证明这个结论吗？试试看.‎ 已知：在四边形ABCD中，O是对角线BD上任意一点（如图7）；‎ 求证：S△OBC·S△OAD=S△OAB·S△OCD.‎ 图7‎ ‎ (2)在三角形中（如图8），你能否归纳出类似的结论？若能，写出你猜想的结论，并证明：若不能，说明理由.‎ 图8‎ 分析：（1）分别过点A、C，做AE⊥DB，交DB的延长线于E，CF⊥BD于F，‎ 则有：S△AOBBO·AE ‎ S△CODDO·CF ‎ S△AODDO·AE ‎ S△BOCBO·CF ‎∴S△AOB ·S△CODBO·DO·AE·CF ‎ S△AOD·S△BOC BO·DO·CF·AE ‎∴S△AOB ·S△COD ＝S△AOD·S△BOC.‎ ‎（2）根据“乘除乘方不改变”能猜想到：从三角形的一个顶点与对边上任意一点的连线上任取一点，与三角形的另外两个顶点连线，将三角形分成四个小三角形，其中相对的两对三角形的面积之积相等. 或S△AOD·S△BOC＝S△AOB ·S△DOC ‎ 已知：在△ABC中，D为AC上一点，O为BD上一点 求证：S△AOD·S△BOC＝S△AOB ·S△DOC 证明：分别过点A、C，作AE⊥BD，交BD的延长线于E，作CF⊥BD于F，‎ 则有：S△AODDO·AE，S△BOCBO·CF ‎ S△OABOB·AE，S△DOCOD·CF ‎ ∴S△AOD·S△BOC OB·OD·AE·CF ‎ S△OAB ·S△DOCBO·OD·AE·CF ‎ ∴S△AOD·S△BOC＝S△OAB ·S△DOC 五、创新题一隅 ‎1、某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时，进行如下：‎ 甲同学：这种多边形不一定是正多边形，如圆内接矩形；‎ 乙同学：我发现边数是6，它也不一定是正多边形。如图9，△是正三角形，= = ,可以证明六边形ADBECF的各角相等，但它未必是正六边形；‎ 丙同学：我能证明，边数是5时，它是正多边形。我想，边数是7时，它可能是正多边形。‎ ‎……‎ ‎（1）请你说明乙同学构造的六边形各角相等；‎ ‎（2）请你证明，各角都相等的圆内接七边形ABCDEFG（如图10）是正七边形（不必写已知、求证）；‎ ‎（3）根据以上探索过程，提出你的猜想（不必证明）；‎ 图9 图10‎ ‎2、如图11是某段河床横断面的示意图.查阅该河段的水文资料，得到下表中的数据：‎ x x y 图11‎ x(米)‎ ‎5‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ y(米)‎ ‎0.125‎ ‎0.5‎ ‎2‎ ‎4.5‎ ‎8‎ ‎12.5‎ ‎10‎ O 图12‎ y(米)‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎12‎ ‎14‎ ‎2‎ x(米)‎ ‎60‎ ‎50‎ ‎40‎ ‎30‎ ‎20‎ y ‎（1）请你以上表中的各对数据（x，y）作为点的坐标，尝试在图12所示的坐标系中画出y关于x的函数图象；‎ ‎（2）①填写下表：‎ x ‎5‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎②根据所填表中数据呈现的规律，猜想出用x表示y 的二次函数的表达式：_______.‎ ‎（3）当水面宽度为‎36米时，一艘吃水深度（船底部到水面的距离）为‎1.8米的货船能否在这个河段安全通过？为什么？‎ 参考答案：‎ ‎1、（1）略；‎ ‎（2）略；‎ ‎（3）猜想：各内角都相等的圆内接多边形的变数为奇数时，它是正多边形；边数为偶数时，它不一定是正多边形。‎ ‎2、（1）图象如图13所示.‎ O ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ x/m ‎2‎ ‎14‎ ‎12‎ ‎10‎ ‎8‎ ‎6‎ ‎4‎ y/m 图13‎ ‎（2）① 根据题意，可以填写下表： ‎ x ‎5‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎200‎ ‎200‎ ‎200‎ ‎200‎ ‎200‎ ‎200‎ ‎② ‎ ‎（3）当水面宽度为‎36米时，相应的x为18，此时水面中心的 因为货船吃水深度为‎1.8m，显然，1.62<1.8,所以当水面宽度为‎36米时，该货船不能通过这个河段.‎