中考压轴题圆含答案 48页

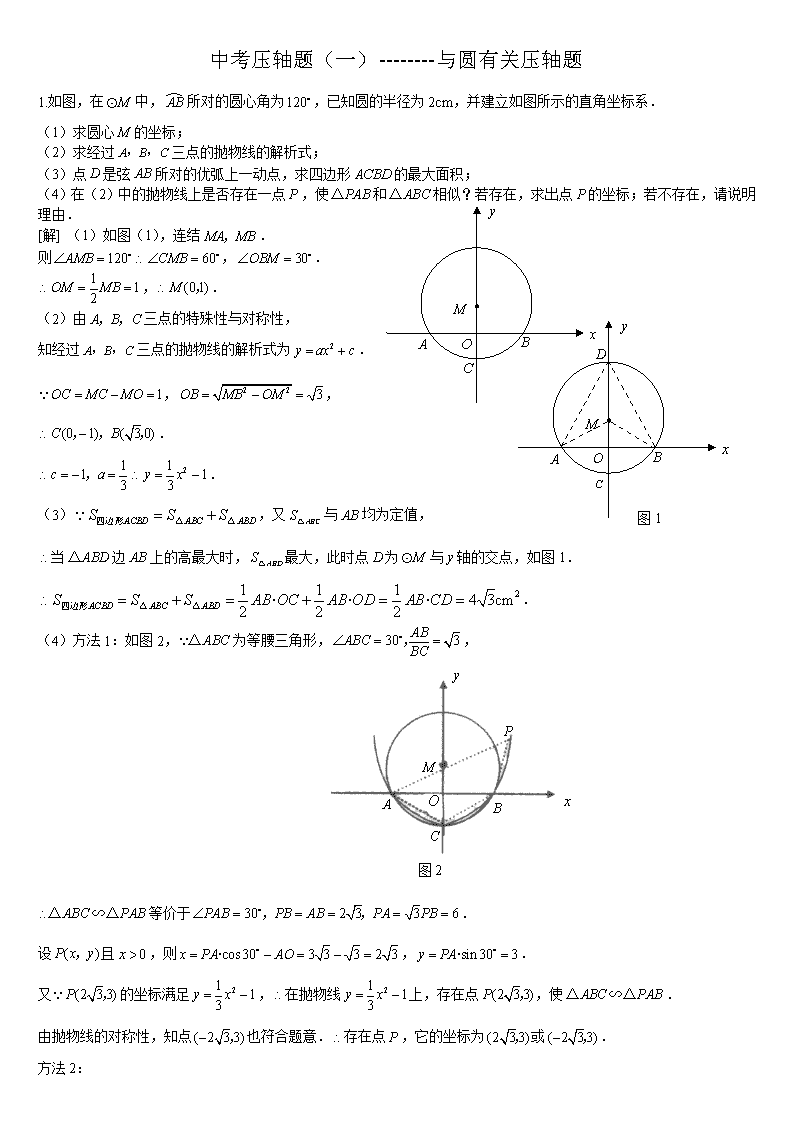
中考压轴题（一）--------与圆有关压轴题 ‎1.如图，在中，所对的圆心角为，已知圆的半径为2cm，并建立如图所示的直角坐标系．‎ ‎（1）求圆心的坐标；‎ ‎（2）求经过三点的抛物线的解析式；‎ ‎（3）点是弦所对的优弧上一动点，求四边形的最大面积；‎ ‎（4）在（2）中的抛物线上是否存在一点，使和相似？若存在，求出点的坐标；若不存在，请说明理由．‎ ‎[解] （1）如图（1），连结．‎ 则，． ‎ ‎，． ‎ 图1‎ ‎（2）由三点的特殊性与对称性，‎ 知经过三点的抛物线的解析式为． ‎ ‎，，‎ ‎． ‎ ‎． ‎ ‎（3），又与均为定值， ‎ 当边上的高最大时，最大，此时点为与轴的交点，如图1．‎ ‎． ‎ ‎（4）方法1：如图2，为等腰三角形，，‎ 图2‎ 等价于． ‎ 设且，则，． ‎ 又的坐标满足，在抛物线上，存在点，使．‎ 由抛物线的对称性，知点也符合题意．存在点，它的坐标为或． ‎ 方法2：‎ 如图（3），当时，，又由（1）知，‎ 点在直线上．‎ 设直线的解析式为，‎ 将代入，解得直线的解析式为． ‎ 解方程组得． ‎ 又，．，．‎ 在抛物线上，存在点，使．‎ 由抛物线的对称性，知点也符合题意．存在点，它的坐标为或． ‎ 方法3：‎ 如图3，为等腰三角形，且，设则 图3‎ 等价于，． ‎ 当时，得解得． ‎ 又的坐标满足，在抛物线上，存在点，使．‎ 由抛物线的对称性，知点也符合题意．存在点，它的坐标为或． ‎ ‎[点评]本题是一道综合性很强也是传统型的压轴题，涉及了函数、方程、相似、圆等大量初中数学的重点知识，解这类问题要求学生必须稳固的掌握各个领域的数学知识，须注意的是在第4小问中涉及了相似三角形的问题，很有可能会有多解的情况出现，此时就要求学生拥有较强的数形结合思想去探索结论的存在性。‎ ‎2.（06湖南湘潭卷）已知：如图，抛物线的图象与轴分别交于两点，与轴交于点，经过原点及点，点是劣弧上一动点（点与不重合）．‎ ‎（1）求抛物线的顶点的坐标；‎ ‎（2）求的面积；‎ ‎（3）连交于点，延长至，使，试探究当点运动到何处时，直线与相切，并请说明理由．‎ ‎[解] （1）抛物线 ‎　　　　　　　　‎ ‎　　　　　　　　　　的坐标为　　‎ ‎（2）连；过为的直径．　　‎ 而　　　　　　‎ ‎（3）当点运动到的中点时，直线与相切　　‎ 理由：在中，．‎ 点是的中点 ‎，　　‎ 在中，为等边三角形 ‎　　又为直径，当为的中点时，为的切线　　‎ ‎[点评]本题将抛物线与圆放在同一坐标系中研究，因此数形结合的解题思想是不可缺少的，解第3小问时可以先自己作图来确定D点的位置。‎ ‎3．（06湖南永州卷）如图，以为圆心的两个同心圆中，大圆的直径交小圆于两点，大圆的弦切小圆于点，过点作直线，垂足为，交大圆于两点．‎ ‎（1）试判断线段与的大小关系，并说明理由．‎ ‎（2）求证：．‎ ‎（3）若是方程的两根（），求图中阴影部分图形的周长．‎ A B C D E O N H M F ‎[解] （1）相等． ‎ 连结，则，故． ‎ ‎（2）由，得， ‎ 又由，得． ． ‎ ‎（3）解方程得：，， ，，‎ 在中，，，．‎ 在中，，‎ ‎，，‎ 弧长，， ‎ 阴影部分周长． ‎ ‎[点评]本题是比较传统的几何型综合压轴题，涉及圆、相似、三角等几何重点知识。‎ ‎4. （06辽宁卷）如图，已知，以点为圆心，以长为半径的圆交轴于另一点，过点作交于点，直线交轴于点．‎ ‎（1）求证：直线是的切线；‎ ‎（2）求点的坐标及直线的解析式；‎ x y A B C O F E ‎（3）有一个半径与的半径相等，且圆心在轴上运动的．若与直线相交于两点，是否存在这样的点，使是直角三角形．若存在，求出点的坐标；若不存在，请说明理由．‎ ‎[解] （1）证明：连结 ‎ 又 又 是的切线．‎ ‎（2）方法①由（1）知 ‎，，　　　　　①‎ 又，　　　　②‎ 由①②解得（舍去）或，‎ 直线经过，两点设的解析式：‎ 解得直线的解析式为． ‎ 方法②：切于点，‎ 又，，即　　　　　①‎ 又，　　　　　②‎ 由①②解得（舍去）或 （求的解析式同上）．‎ 方法③，　　　　　①‎ 切于点，，‎ ‎， 　　　　② 由①②解得：， （求的解析式同上）．‎ ‎（3）存在；‎ 当点在点左侧时，若，过点作于点，‎ ‎，，‎ ‎，，，‎ ‎，， ‎ 当点在点右侧时，设，过点作于点，则 x y A B C O P F M E H N Q ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎，可知与关于点中心对称，‎ 根据对称性得 存在这样的点，使得为直角三角形，‎ 点坐标或．‎ ‎[点评]本题是一道综合性很强的传统型压轴题，其难度比较恰当，选拔功能较强，解第3小题时要注意分类讨论，这是本题最容易失分的地方 ‎5. （06辽宁沈阳卷）如图，在平面直角坐标系中，直线分别与轴，轴交于点，点．‎ ‎（1）以为一边在第一象限内作等边及的外接圆（用尺规作图，不要求写作法，但要保留作图痕迹）；‎ ‎（2）若与轴的另一个交点为点，求，，，四点的坐标；‎ ‎（3）求经过，，三点的抛物线的解析式，并判断在抛物线上是否存在点，使的面积等于的面积？若存在，请直接写出所有符合条件的点的坐标；若不存在，请说明理由．‎ ‎[解] （1）如图，正确作出图形，保留作图痕迹 ‎（2）由直线，求得点的坐标为，点的坐标为 在中，，‎ ‎，‎ 是等边三角形，‎ 点的坐标为，连结 是等边三角形 直线是的切线点的坐标为 ‎（3）设经过，，三点的抛物线的解析式是 把代入上式得抛物线的解析式是 存在点，使的面积等于的面积 点的坐标分别为，．‎ ‎[点评]本题是一道综合性很强的压轴题，主要考查二次函数、一次函数、圆、几何作图等大量知识，第3小题是比较常规的结论存在性问题，运用方程思想和数形结合思想可解决。‎ ‎6.已知：抛物线与轴相交于两点，且．‎ ‎（Ⅰ）若，且为正整数，求抛物线的解析式；（Ⅱ）若，求的取值范围；‎ ‎（Ⅲ）试判断是否存在，使经过点和点的圆与轴相切于点，若存在，求出的值；若不存在，试说明理由；‎ ‎（Ⅳ）若直线过点，与（Ⅰ）中的抛物线相交于两点，且使，求直线的解析式．‎ ‎[解] （Ⅰ）解法一：由题意得， ． 解得，．为正整数，．． ‎ ‎ 解法二：由题意知，当时，． 以下同解法一）‎ ‎ 解法三：， ．‎ ‎ 又． ．（以下同解法一．）‎ ‎ 解法四：令，即，．（以下同解法三．）‎ Ａ Ｂ x Ｄ y O ‎（Ⅱ）解法一：．，‎ 即． ‎ ‎ ‎ ‎．解得 的取值范围是．‎ ‎ 解法二：由题意知，当时，‎ ‎ ． 解得：．的取值范围是． ‎ ‎ 解法三：由（Ⅰ）的解法三、四知，．‎ ‎ ， ．的取值范围是． ‎ ‎（Ⅲ）存在．‎ ‎ 解法一：因为过两点的圆与轴相切于点，所以两点在轴的同侧，． ‎ ‎ 由切割线定理知，， 即．，‎ ‎ ． ‎ ‎ 解法二：连接．圆心所在直线， ‎ ‎ 设直线与轴交于点，圆心为， 则．‎ ‎ ， ． ‎ ‎ 在中， ． 即．解得 ．‎ ‎（Ⅳ）设，则．‎ y x Ｏ Ｐ Ｑ Ｆ ‎7‎ ‎ 过分别向轴引垂线，垂足分别为．‎ ‎ 则．‎ ‎ 所以由平行线分线段成比例定理知，．‎ ‎ 因此，，即． ‎ ‎ 过分别向轴引垂线，垂足分别为，‎ ‎ 则．所以．．‎ ‎ ．． ，或． ‎ ‎ 当时，点．直线过， 解得 ‎ 当时，点．直线过，‎ ‎ 解得故所求直线的解析式为：，或． ‎ ‎7. 如图，在平面直角坐标系中，已知点，，以为边在轴下方作正方形，点是线段与正方形的外接圆除点以外的另一个交点，连结与相交于点．‎ ‎（1）求证：；‎ ‎（2）设直线是的边的垂直平分线，且与相交于点．若是的外心，试求经过三点的抛物线的解析表达式；‎ A E O D C B G F x y l ‎（3）在（2）的条件下，在抛物线上是否存在点，使该点关于直线的对称点在轴上？若存在，求出所有这样的点的坐标；若不存在，请说明理由．‎ ‎[解] （1）在和中，‎ 四边形是正方形，．‎ 又，‎ ‎．　　‎ ‎（2）由（1），有，．点．‎ 是的外心，点在的垂直平分线上．点也在的垂直平分线上．为等腰三角形，．‎ 而，．‎ ‎．‎ 设经过三点的抛物线的解析表达式为．‎ 抛物线过点，．．　　 ①‎ 把点，点的坐标代入①中，得 即　　解得 抛物线的解析表达式为． ②‎ ‎（3）假定在抛物线上存在一点，使点关于直线的对称点在轴上．是的平分线，‎ 轴上的点关于直线的对称点必在直线上，即点是抛物线与直线的交点．‎ A E O D C B G F x y l Q 设直线的解析表达式为，并设直线与轴交于点，则由是等腰直角三角形．‎ ‎．．‎ 把点，点代入中，得 直线的解析表达式为．‎ 设点，则有．　　 ③‎ 把③代入②，得，‎ ‎，即．‎ ‎．解得或．‎ 当时，；当时，．‎ 在抛物线上存在点，它们关于直线的对称点都在轴上．‎ ‎8.在平面直角坐标系xOy中，已知直线l1经过点A(-2，0)和点B(0，)，直线l2的函数表达式为，l1与l2相交于点P．⊙C是一个动圆，圆心C在直线l1上运动，设圆心C的横坐标是a．过点C作CM⊥x轴，垂足是点M．‎ ‎(1)　填空：直线l1的函数表达式是 ，交点P的坐标是 ，∠FPB的度数是 ；‎ ‎(2)　当⊙C和直线l2相切时，请证明点P到直线CM的距离等于⊙C的半径R，并写出R=时a的值.‎ ‎(3)　当⊙C和直线l2不相离时，已知⊙C的半径R=，记四边形NMOB的面积为S(其中点N是直线CM与l2的交点)．S是否存在最大值？若存在，求出这个最大值及此时a的值；若不存在，请说明理由．‎ ‎2‎ ‎1‎ ‎3‎ ‎4‎ ‎1‎ ‎2‎ ‎3‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-1‎ y x O A B E F P l1‎ l2‎ C 图2‎ N M ‎[解] (1) P(1，) 60º ‎2‎ ‎1‎ ‎3‎ ‎4‎ ‎1‎ ‎2‎ ‎3‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-1‎ y x O A B E F P l1‎ l2‎ C ‎(第24题图甲)‎ G D M ‎ (2)　设⊙C和直线l2相切时的一种情况如图甲所示，D是切点，连接CD，则CD⊥PD．‎ 过点P作CM的垂线PG，垂足为G，则Rt△CDP≌Rt△PGC (∠PCD=∠CPG=30º，CP=PC)， 所以PG=CD=R． ‎ 当点C在射线PA上，⊙C和直线l2相切时，同理可证．取R=时，a=1+R=，或a=-(R-1)‎ ‎(3) 当⊙C和直线l2不相离时，由(2)知，分两种情况讨论：‎ ‎① 如图乙，当0≤a≤时，， ‎ 当时，（满足a≤），S有最大值．此时（或）．‎ ‎② 当≤a＜0时，显然⊙C和直线l2相切即时，S最大．此时 ‎． ‎ ‎ 综合以上①和②，当或时，存在S的最大值，其最大面积为 ‎ ‎9. 如图1，已知中，，．过点作，且，连接交于点．‎ ‎（1）求的长；‎ ‎（2）以点为圆心，为半径作，试判断与是否相切，并说明理由；‎ ‎（3）如图2，过点作，垂足为．以点为圆心，为半径作；以点为圆心，为半径作．若和的大小是可变化的，并且在变化过程中保持和相切，且使点在的内部，点在的外部，求和的变化范围．‎ A B C P E E A B C P Ｄ 图1‎ 图2‎ ‎[解] （1）在中，，． ‎ ‎　　　　，．．，． ‎ ‎　　（2）与相切． 在中，，，‎ ‎　　　　，． ‎ ‎　　　　又，与相切． ‎ ‎　　（3）因为，所以的变化范围为． ‎ ‎　　　　当与外切时，，所以的变化范围为；‎ ‎　　　　当与内切时，，所以的变化范围为．‎ ‎[点评]本题是一道比较传统的几何综合题，第1题运用相似三角形知识即可得解，第2小题也较基础，第3小题注意要分类，试题中只说明了“和相切”，很多同学漏解往往是由于没有仔细读题和审题。‎ ‎8，（06江苏宿迁课改卷）设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．‎ ‎（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：‎ d、a、r之间关系 公共点的个数 d＞a＋r 图①‎ d＝a＋r a－r＜d＜a＋r d＝a－r d＜a－r 所以，当r＜a时，⊙O与正方形的公共点的个数可能有　　　　　　　　　个；‎ ‎（2）如图②，当r＝a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：‎ d、a、r之间关系 图②‎ 公共点的个数 d＞a＋r d＝a＋r a≤d＜a＋r d＜a 所以，当r＝a时，⊙O与正方形的公共点个数可能有　　　　　　　　个；‎ 图③‎ ‎（3）如图③，当⊙O与正方形有5个公共点时，试说明r＝a；‎ ‎（4）就r＞a的情形，请你仿照“当……时，⊙O与正方形的公共点个数可能有 ‎　 　 个”的形式，至少给出一个关于“⊙O与正方形的公共点个数”的正确结论．‎ ‎[解] （1）‎ d、a、r之间关系 公共点的个数 d＞a＋r ‎0‎ d＝a＋r ‎1‎ a－r＜d＜a＋r ‎2‎ d＝a－r ‎1‎ d＜a－r ‎0‎ 图①‎ ‎ ‎ ‎ 所以，当r＜a时，⊙O与正方形的公共点的个数可能有0、1、2个； ‎ 图②‎ ‎（2）‎ d、a、r之间关系 公共点的个数 d＞a＋r ‎0‎ d＝a＋r ‎1‎ a≤d＜a＋r ‎2‎ d＜a ‎4‎ 所以，当r＝a时，⊙O与正方形的公共点个数可能有0、1、2、4个； ‎ ‎（3）方法一：如图所示，连结OC则OE＝OC＝r ，OF＝EF－OE＝2a－r． ‎ B C D F E ‎ 在Rt△OCF中，由勾股定理得：‎ ‎ OF2＋FC2＝OC2‎ 即（2a－r）2＋a2＝r2 ‎ ‎ 4a2－4ar＋r2＋a2＝r2‎ ‎ 5a2＝4ar ‎5a＝4r ‎ ‎∴r ＝a． ‎ B N E 方法二：如图，连结BD、OE、BE、DE． ‎ ‎∵四边形BCMN为正方形 ‎∴∠C＝∠M＝∠N＝90°‎ ‎∴BD为⊙O的直径，∠BED＝90°‎ M D ‎∴∠BEN＋∠DEM ＝90°‎ C ‎∵∠BEN＋∠EBN＝90°‎ ‎∴∠DEM＝∠EBN ‎∴△BNE∽△EMD ∴∴DM＝a ‎ 由OE是梯形BDMN的中位线得OE＝（BN＋MD）＝a．‎ ‎（4）①当a＜r＜时，⊙O与正方形的公共点个数可能有0、1、2、4、6、7、8个；‎ ‎②当r＝a时，⊙O与正方形的公共点个数可能有0、1、2、5、8个；‎ ‎③当时，⊙O与正方形的公共点个数可能有0、1、2、3、4、6、8个；‎ ‎④当时，⊙O与正方形的公共点个数可能有0、1、2、3、4个；‎ ‎⑤当时，⊙O与正方形的公共点个数可能有0、1、2、3、4个．‎ ‎[点评]本题是一道较为新颖的几何压轴题，考查圆、相似、正方形等几何知识，综合性较强，有一定的难度，试题的区分度把握非常得当，是一道很不错的压轴题。‎ ‎9. （06山东枣庄课改卷）半径为2.5的⊙O中，直径AB的不同侧有定点C和动点P．已知BC ：CA＝4 : 3，点P在上运动，过点C作CP的垂线，与PB的延长线交于点O ‎（1）当点P与点C关于AB对称时，求CQ的长；‎ ‎（2）当点P运动到的中点时，求CQ的长； ‎ ‎（3）当点P运动到什么位置时，CQ取到最大值？求此时CQ的长．‎ ‎[解] （1）当点P与点C关于AB对称时，CP⊥AB，设垂足为D. ‎ ‎ ∵AB为⊙O的直径，∴∠ACB=900.‎ ‎ ∴AB=5,AC:CA=4:3,∴BC=4, AC=3.‎ ‎ 又∵AC·BC=AB·CD ‎ ‎ ‎∴ ‎ ‎ 在Rt△ACB和Rt△PCQ中，‎ ‎ ∠ACB＝∠PCQ=900, ∠CAB＝∠CPQ，‎ ‎ Rt△ACB∽Rt△PCQ ‎ ∴ ‎ ‎ （2）当点P运动到弧AB的中点时，过点B作BE⊥PC 于点E（如图）.∵P是弧AB的中点，∴ ‎ ‎ 又∠CPB=∠CAB∴∠CPB= tan∠CAB=‎ ‎ ∴而从 ‎ ‎ 由（l）得， ‎ ‎ （3）点P在弧AB上运动时，恒有 ‎ 故PC最大时，CQ取到最大值． ‎ ‎ 当PC过圆心O，即PC取最大值5时，CQ 最大值为 ‎ ‎[点评]本题属于常规的几何综合题，解第3小问时要有动态的思想（在草稿上画画图）不难猜想出结论。‎ ‎10.如图，点在轴上，交轴于两点，连结并延长交于，过点的直线交轴于，且的半径为，．‎ ‎（1）求点的坐标；‎ ‎（2）求证：是的切线；‎ Ｄ Ａ Ｃ ＰＣ ＢＣ ＯＣ ‎（3）若二次函数的图象经过点，求这个二次函数的解析式，并写出使二次函数值小于一次函数值的的取值范围．‎ ‎[解] （1）如图，连结　 　， ‎ 是的直径（也可用勾股定理求得下面的结论）　，　 ，，‎ ‎　　（2）过点　 ‎ 当时，　　 Ｄ Ａ Ｃ ＰＣ ＢＣ ＯＣ ，　　‎ ‎　　‎ ‎　　（也可用勾股定理逆定理证明）‎ ‎　　是的切线 ‎　　（3）过点 ‎　 ‎ 因为函数与的图象交点是和点（画图可得此结论）‎ 所以满足条件的的取值范围是或 ‎ ‎11. 如图，在平面直角坐标系中，以坐标原点O为圆心，2为半径画⊙O，P是⊙O上一动点，且P在第一象限内，过点P作⊙O的切线与轴相交于点A，与轴相交于点B。‎ ‎（1）点P在运动时，线段AB的长度在发生变化，请写出线段AB长度的最小值，并说明理由；‎ ‎（2）在⊙O上是否存在一点Q，使得以Q、O、A、P为顶点的四边形时平行四边形？若存在，请求出Q点的坐标；若不存在，请说明理由。‎ ‎[解] （1）线段AB长度的最小值为4‎ ‎ 理由如下：连接OP ‎ 因为AB切⊙O于P，所以OP⊥AB ‎ 取AB的中点C，则 ‎ ‎ 当时，OC最短， 即AB最短，此时 ‎ ‎ （2）设存在符合条件的点Q，‎ 如图①，设四边形APOQ为平行四边形，‎ 因为四边形APOQ为矩形又因为所以四边形APOQ为正方形 所以，‎ 在Rt△OQA中，根据，得Q点坐标为（）。 ‎ 如图②，设四边形APQO为平行四边形因为OQ∥PA，，所以，又因为所以，‎ 因为 PQ∥OA，所以 轴。设轴于点H，‎ 在Rt△OHQ中，根据，得Q点坐标为（）‎ 所以符合条件的点Q的坐标为（）或（）。‎ ‎12. 如图①，在平面直角坐标系中，以坐标原点O为圆心的⊙O的半径为，直线l：‎ 与坐标轴分别交于A、C两点，点B的坐标为(4，1)，⊙B与x轴相切于点M。‎ ‎（1）求点A的坐标及∠CAO的度数；‎ ‎（2）⊙B以每秒1各单位长度的速度沿x轴负方向平移，同时，直线l绕点A顺时针匀速旋转。当⊙B第一次与⊙O相切时，直线l也恰好与⊙B第一次相切。问：直线AC绕点A每秒旋转多少度？‎ A B O M C y x 第25题图①‎ A E O C y x 第25题图②‎ O1‎ ‎（3）如图②，过A、O、C三点作⊙O1，点E为劣弧AO上一点，连接EC、EA、EO，当点E在劣弧AO上运动时(不与A、O两点重合)，的值是否发生变化？如果不变，求其值；如果变化，说明理由。‎ ‎13. （06广东深圳课改卷）(10分)如图10-1，在平面直角坐标系中，点在轴的正半轴上， ⊙交轴于 两点，交轴于两点，且为的中点，交轴于点，若点的坐标为（－2，0），‎ ‎(1)(3分)求点的坐标. ‎ ‎(2)(3分)连结，求证：∥‎ ‎(3)(４分) 如图10-2，过点作⊙的切线，交轴于点.动点在⊙的圆周上运动时，的比值是否发生变化，若不变，求出比值；若变化，说明变化规律.‎ ‎ ‎ ‎14.(06 安徽芜湖市课改卷）一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘，如图所示，AB与C D是水平的，BC与水平面的夹角为600，其中AB=60cm，CD=40cm，BC=40cm，请你作出该小朋友将园盘从A点滚动到D点其圆心所经过的路线的示意图，并求出此路线的长度。‎ ‎15. (07芜湖市)24. 已知圆P的圆心在反比例函数图象上，并与x轴相交于A、B两点． 且始终与y轴相切于定点C(0，1)．‎ (1) 求经过A、B、C三点的二次函数图象的解析式;‎ (2) 若二次函数图象的顶点为D，问当k为何值时，四边形ADBP为菱形．‎ 解: (1)连结PC、PA、PB，过P点作PH⊥x轴，垂足为H． ‎ ‎∵⊙P与轴相切于点C (0，1)，∴PC⊥轴．‎ ‎∵P点在反比例函数的图象上，‎ ‎∴P点坐标为（k，1）． ∴PA=PC=k．‎ 在Rt△APH中，AH==，‎ ‎∴OA=OH—AH=k－． ‎ ‎∴A（k－，0）． ‎ ‎∵由⊙P交x轴于A、B两点，且PH⊥AB，由垂径定理可知， PH垂直平分AB．‎ ‎∴OB=OA+2AH= k－+2=k+，∴B(k+，0)． ‎ 故过A、B两点的抛物线的对称轴为PH所在的直线解析式为x=k．‎ 可设该抛物线解析式为y=a+h． ‎ 又抛物线过C(0，1)， B(k+，0)， 得： ‎ ‎ ‎ 解得a=1，h=1－． ‎ ‎∴抛物线解析式为y=+1－．‎ ‎（2）由(1)知抛物线顶点D坐标为（k， 1－）∴DH=－1． ‎ 若四边形ADBP为菱形．则必有PH=DH ．∵PH=1，∴－1=1． 又∵k＞1，∴k= ‎ ‎∴当k取时，PD与AB互相垂直平分，则四边形ADBP为菱形．‎ ‎16. 26. 如图①，②，在平面直角坐标系中，点的坐标为(4，0)，以点为圆心，4为半径的圆与轴交于，两点，为弦，，是轴上的一动点，连结．‎ ‎（1）求的度数；（2分）（2）如图①，当与相切时，求的长；（3分）‎ ‎（3）如图②，当点在直径上时，的延长线与相交于点，问为何值时，是等腰三角形？）‎ 解：（1）∵，，∴是等边三角形． ∴． ‎ ‎（2）∵CP与相切，∴． ∴．‎ 又∵（4，0），∴．∴．‎ ‎∴． ‎ ‎（3）①过点作，垂足为，延长交于，‎ ‎∵是半径， ∴，∴，∴是等腰三角形．‎ 又∵是等边三角形，∴=2 ．‎ ‎②解法一：过作，垂足为，延长交于，与轴交于，‎ ‎∵是圆心， ∴是的垂直平分线． ∴．∴是等腰三角形， ‎ 过点作轴于，在中，∵，‎ ‎∴．∴点的坐标（4+，）．‎ 在中，∵，∴．∴点坐标（2，）．　‎ 设直线的关系式为：，则有 ‎ 解得：∴．当时，．∴．　‎ 解法二： 过A作，垂足为，延长交于，与轴交于，‎ ‎∵是圆心， ∴是的垂直平分线． ∴．∴是等腰三角形．‎ ‎∵，∴．∵平分，∴．‎ ‎∵是等边三角形，， ∴． ∴．‎ ‎∴是等腰直角三角形．∴．∴．‎ ‎17. 26. 如图12-1所示，在中，，，为的中点，动点在边上自由移动，动点在边上自由移动．‎ ‎（1）点的移动过程中，是否能成为的等腰三角形？若能，请指出为等腰三角形时动点的位置．若不能，请说明理由．‎ ‎（2）当时，设，，求与之间的函数解析式，写出的取值范围．‎ ‎（3）在满足（2）中的条件时，若以为圆心的圆与相切（如图12-2），试探究直线与的位置关系，并证明你的结论．‎ 图12-1‎ 图12-2‎ A E F O C B A E F O C B ‎（图12－1）‎ ‎（图12－2）‎ 解：如图，‎ ‎（1）点移动的过程中，能成为的等腰三角形．此时点的位置分别是：‎ ‎①是的中点，与重合．‎ ‎②．③与重合，是的中点 ‎（2）在和中，，，‎ ‎．又，．．‎ ‎，，，．‎ ‎（3）与相切．，．．即．‎ 又，．．点到和的距离相等．‎ 与相切，点到的距离等于的半径．与相切．‎ ‎18. (06武汉市) 如图①，在平面直角坐标系中，Rt△AOB≌Rt△CDA，且A(－1，0)、B(0，2)，抛物线y＝ax2＋ax－2经过点C。(1)求抛物线的解析式；‎ ‎(2)在抛物线(对称轴的右侧)上是否存在两点P、Q，使四边形ABPQ是正方形？若存在，求点P、Q的坐标，若不存在，请说明理由；‎ ‎(3)如图②，E为BC延长线上一动点，过A、B、E三点作⊙O’，连结AE，在⊙O’上另有一点F，且AF＝AE，AF交BC于点G，连结BF。下列结论：①BE＋BF的值不变；②，其中有且只有一个成立，请你判断哪一个结论成立，并证明成立的结论。‎ O x y B F A E C O’‎ G ‎(第25题图②)‎ O ‎(第25题图①)‎ A B C D x y 解：⑴由Rt△AOB≌Rt△CDA得OD=2+1=3,CD=1∴C点坐标为(－3,1),‎ ‎∵抛物线经过点C,∴1= (－3)2 a＋(－3)ａ－2，∴。∴抛物线的解析式为.‎ ‎⑵在抛物线（对称轴的右侧）上存在点P、Q，使四边形ABPQ是正方形。‎ 以AB边在AB右侧作正方形ABPQ。过P作PE⊥OB于E，QG⊥x轴于G，可证△PBE≌△AQG≌△BAO，‎ ‎∴PE＝AG＝BO＝2，BE＝QG＝AO＝1，∴∴P点坐标为（2,1），Q点坐标为（1,－1）。‎ 由（1）抛物线。当x＝2时，y＝1，当x＝,1时，y＝－1。∴P、Q在抛物线上。‎ 故在抛物线（对称轴的右侧）上存在点P（2,1）、Q（1,－1），使四边形ABPQ是正方形。‎ ‎⑵另解：在抛物线（对称轴的右侧）上存在点P、Q，使四边形ABPQ是正方形。‎ 延长CA交抛物线于Q，过B作BP∥CA交抛物线于P，连PQ，设直线CA、BP的解析式分别为y=k1x+b1, y=k2x+b2,‎ ‎∵A（－1,0），C（－3,1），∴CA的解析式，同理BP的解析式为，‎ 解方程组得Q点坐标为（1,－1），同理得P点坐标为（2,1）。‎ 由勾股定理得AQ＝BP＝AB＝，而∠BAQ＝90°，‎ ‎∴四边形ABPQ是正方形。故在抛物线（对称轴的右侧）上存在点P（2,1）、Q（1,－1），使四边形ABPQ是正方形。‎ ‎⑵另解：在抛物线（对称轴的右侧）上存在点P、Q，使四边形ABPQ是正方形。如图，将线段CA沿CA方向平移至AQ，∵C（－3,1）的对应点是A（－1,0），∴A（－1,0）的对应点是Q（1,－1），再将线段AQ沿AB方向平移至BP，同理可得P（2,1）‎ ‎∵∠BAC＝90°，AB＝AC ‎∴四边形ABPQ是正方形。经验证P（2,1）、Q（1,－1）两点均在抛物线上。‎ ‎⑶结论②成立，‎ 证明如下：连EF，过F作FM∥BG交AB的延长线于M，则△AMF∽△ABG，∴。‎ 由⑴知△ABC是等腰直角三角形，∴∠1＝∠2＝45°。∵AF＝AE，∴∠AEF＝∠1＝45°。‎ ‎∴∠EAF＝90°，EF是⊙O´的直径。∴∠EBF＝90°。∵FM∥BG，‎ ‎∴∠MFB＝∠EBF＝90°，∠M＝∠2＝45°，∴BF＝MF，∴‎ ‎ 24、如图12，形如三角板的∆ABC中，∠ACB=90°,∠ABC=45°,BC=12cm，形如矩形量角器的半圆O的直径DE=12cm,矩形DEFG的宽EF=6cm，矩形量角器以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在BC所在的直线上，设运动时间为x（s），矩形量角器和∆ABC的重叠部分的面积为S(cm2).当x=0(s)时，点E与点C重合.(图（3）、图（4）、图（5）供操作用).‎ ‎（1）当x=3时，如图（2），S= cm2,‎ 当x=6时，S= cm2，‎ 当x=9时，S= cm2；‎ ‎（2）当30），则N（R+1，R），‎ 代入抛物线的表达式，解得 ‎②当直线MN在x轴下方时，设圆的半径为r（r>0），则N（r+1，－r），‎ 代入抛物线的表达式，解得 ‎ ‎∴圆的半径为或．‎ ‎（4）过点P作y轴的平行线与AG交于点Q，易得G（2，－3），直线AG为．‎ 设P（x，），则Q（x，－x－1），PQ．‎ ‎ ‎ 当时，△APG的面积最大 此时P点的坐标为，． ‎ ‎33.（08湖南长沙）26.如图，六边形ABCDEF内接于半径为r（常数）的⊙O，其中AD为直径，且AB=CD=DE=FA.‎ ‎（1）当∠BAD=75°时，求的长；（2）求证：BC∥AD∥FE；‎ A B C D E F O ‎·‎ ‎（3）设AB=，求六边形ABCDEF的周长L关于的函数关系式，并指出为何值时，L取得最大值.‎ ‎（08湖南长沙26题解析）26．(1)连结OB、OC，由∠BAD=75°，OA=OB知∠AOB=30° ‎∵AB=CD，∴∠COD=∠AOB=30°，∴∠BOC=120°，故的长为．‎ ‎(2)连结BD，∵AB=CD，∴∠ADB=∠CBD，∴BC∥AD，同理EF∥AD，从而BC∥AD∥FE．‎ ‎(3)过点B作BM⊥AD于M，由(2)知四边形ABCD为等腰梯形，从而BC=AD-2AM=2r-2AM．‎ ‎∵AD为直径，∴∠ABD=90°，易得△BAM∽△DAB ‎∴AM==，∴BC=2r-，同理EF=2r-‎ ‎∴L=4x+2(2r-)==，其中0＜x＜ ∴当x=r时，L取得最大值6r．‎ ‎34.（08湖南益阳）七、(本题12分)‎ ‎24.我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线.‎ 如图12，点A、B、C、D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为(0，-3)，AB为半圆的直径，半圆圆心M的坐标为(1,0)，半圆半径为2.‎ (1) 请你求出“蛋圆”抛物线部分的解析式，并写出自变量的取值范围；‎ ‎(2)你能求出经过点C的“蛋圆”切线的解析式吗？试试看；‎ ‎(3)开动脑筋想一想，相信你能求出经过点D的“蛋圆”切线的解析式.‎ A O B M D C 图12‎ y x A O B M D C 解图12‎ y x E ‎（08湖南益阳24题解析）七、(本题12分)‎ ‎24．解：(1)解法1：根据题意可得：A(-1,0)，B(3,0)；‎ 则设抛物线的解析式为(a≠0) ‎ 又点D(0，-3)在抛物线上，∴a(0+1)(0-3)=-3，解之得：a=1 ∴y=x2-2x-3自变量范围：-1≤x≤3‎ ‎ 解法2：设抛物线的解析式为(a≠0)根据题意可知，A(-1,0)，B(3,0)，D(0，-3)三点都在抛物线上∴‎ ‎，解之得：∴y=x2-2x-3自变量范围：-1≤x≤3‎ ‎ (2)设经过点C“蛋圆”的切线CE交x轴于点E，连结CM，‎ ‎ 在Rt△MOC中，∵OM=1，CM=2，∴∠CMO=60°,OC=‎ ‎ 在Rt△MCE中，∵OC=2，∠CMO=60°，∴ME=4‎ ‎ ∴点C、E的坐标分别为(0，)，(-3,0) ∴切线CE的解析式为 ‎ (3)设过点D(0，-3)，“蛋圆”切线的解析式为：y=kx-3(k≠0) ‎ ‎ 由题意可知方程组只有一组解 即有两个相等实根，∴k=-2‎ ‎ ∴过点D“蛋圆”切线的解析式y=-2x-3‎ ‎35我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段的最小覆盖圆就是以线段为直径的圆．‎ A A B B C C ‎（第25题图1）‎ ‎（1）请分别作出图1中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；‎ ‎（2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）；‎ G H E F ‎（第25题图2）‎ ‎（3）某地有四个村庄（其位置如图2所示），现拟建一个电视信号中转站，为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小（距离越小，所需功率越小），此中转站应建在何处？请说明理由．‎ ‎（08江苏连云港25题解析）25．解：（1）如图所示：‎ G H E F ‎（第25题答图2）‎ M A A B B C C ‎（第25题答图1）‎ ‎（注：正确画出1个图得2分，无作图痕迹或痕迹不正确不得分）‎ ‎（2）若三角形为锐角三角形，则其最小覆盖圆为其外接圆； 6分 若三角形为直角或钝角三角形，则其最小覆盖圆是以三角形最长边（直角或钝角所对的边）为直径的圆． 8分 ‎（3）此中转站应建在的外接圆圆心处（线段的垂直平分线与线段的垂直平分线的交点处）． ‎ 理由如下：‎ 由，，，‎ 故是锐角三角形，‎ 所以其最小覆盖圆为的外接圆，‎ 设此外接圆为，直线与交于点，‎ 则．‎ 故点在内，从而也是四边形的最小覆盖圆．所以中转站建在的外接圆圆心处，能够符合题中要求．‎ ‎36. （08江苏宿迁）27．（本题满分12分）‎ 如图，⊙的半径为，正方形顶点坐标为，顶点在⊙上运动．‎ ‎(1)当点运动到与点、在同一条直线上时,试证明直线与⊙相切；‎ ‎(2)当直线与⊙相切时，求所在直线对应的函数关系式；‎ ‎(3)设点的横坐标为，正方形的面积为，求与之间的函数关系式，并求出的最大值与最小值．‎ 第27题图2‎ 第27题图1‎ ‎（08江苏宿迁27题解析）27．解：(1) ∵四边形为正方形 ∴‎ ‎∵、、在同一条直线上 ∴ ∴直线与⊙相切；‎ ‎(2)直线与⊙相切分两种情况:‎ ‎①如图1, 设点在第二象限时,过作轴于点,设此时的正方形的边长为,则,解得或(舍去)．由∽ 得 ‎∴　∴，故直线的函数关系式为；‎ ‎　②如图2, 设点在第四象限时,过作轴于点,设此时的正方形的边长为,则,解得或(舍去)．由∽ 得 ‎∴　∴，故直线的函数关系式为.‎ ‎(3)设,则,由得 ‎∴∵∴‎ ‎37. （08江苏无锡）27．（本小题满分10分）‎ 如图，已知点从出发，以1个单位长度/秒的速度沿轴向正方向运动，以为顶点作菱形，使点在第一象限内，且；以为圆心，为半径作圆．设点运动了秒，求：‎ ‎（1）点的坐标（用含的代数式表示）；‎ ‎（2）当点在运动过程中，所有使与菱形的边所在直线相切的的值．‎ y x B C P O A E 图2‎ B A D O P C x y 图1‎ ‎（08江苏无锡27题解析）27．解：（1）过作轴于，‎ ‎，，，，‎ 点的坐标为．‎ ‎（2）①当与相切时（如图1），切点为，此时，，，‎ ‎．‎ ‎②当与，即与轴相切时（如图2），则切点为，，‎ 过作于，则，，．‎ ‎③当与所在直线相切时（如图3），设切点为，交于，‎ 则，，．‎ y x A F C B P O G H 图3‎ 过作轴于，则，‎ ‎，‎ 化简，得，‎ 解得，，‎ ‎．所求的值是，和． （10分）‎ ‎38. （08江苏无锡）28．（本小题满分8分）‎ 一种电讯信号转发装置的发射直径为31km．现要求：在一边长为30km的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：‎ ‎（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？‎ ‎（2）至少需要选择多少个安装点，才能使这些点安装了这种转发装置后达到预设的要求？‎ 答题要求：请你在解答时，画出必要的示意图，并用必要的计算、推理和文字来说明你的理由．（下面给出了几个边长为30km的正方形城区示意图，供解题时选用）‎ 图4‎ 图3‎ 图2‎ 图1‎ ‎（08江苏无锡28题解析）28．解：（1）将图1中的正方形等分成如图的四个小正方形，将这4个转发装置安装在这4个小正方形对角线的交点处，此时，每个小正方形的对角线长为，每个转发装置都能完全覆盖一个小正方形区域，故安装4个这种装置可以达到预设的要求．‎ ‎ （3分）（图案设计不唯一）‎ ‎（2）将原正方形分割成如图2中的3个矩形，使得．将每个装置安装在这些矩形的对角线交点处，设，则，．‎ 由，得，‎ ‎，，‎ 即如此安装3个这种转发装置，也能达到预设要求． （6分）‎ 或：将原正方形分割成如图2中的3个矩形，使得，是 的中点，将每个装置安装在这些矩形的对角线交点处，则，， ，即如此安装三个这个转发装置，能达到预设要求． （6分）‎ 要用两个圆覆盖一个正方形，则一个圆至少要经过正方形相邻两个顶点．如图3，用一个直径为31的去覆盖边长为30的正方形，设经过，与交于，连，则，这说明用两个直径都为31的圆不能完全覆盖正方形．‎ 所以，至少要安装3个这种转发装置，才能达到预设要求．‎ 评分说明：示意图（图1、图2、图3）每个图1分．‎ B F D A E H O 图2‎ 图3‎ D C F B E A O A D C B 图1‎ ‎39. （08山东德州东营菏泽）24．(本题满分12分) ‎ 在△ABC中，∠A＝90°，AB＝4，AC＝3，M是AB上的动点（不与A，B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN．令AM＝x． ‎ ‎（1）用含x的代数式表示△ＭNP的面积S； ‎ ‎（2）当x为何值时，⊙O与直线BC相切？ ‎ ‎（3）在动点M的运动过程中，记△ＭNP与梯形BCNM重合的面积为y，试求y关于x的函数表达式，并求x为何值时，y的值最大，最大值是多少？‎ A B C M N P 图 1‎ O A B C M N P 图 3‎ O A B C M N D 图 2‎ O ‎（08山东德州东营菏泽23题解析）23．(本题满分12分) ‎ 解：（1）∵MN∥BC，∴∠AMN=∠B，∠ANM＝∠C． ‎ A B C M N P 图 1‎ O ‎ ∴ △AMN ∽ △ABC．‎ ‎∴ ，即．‎ ‎∴ AN＝x． ‎ ‎∴ =．（0＜＜4） ‎ A B C M N D 图 2‎ O Q ‎（2）如图2，设直线BC与⊙O相切于点D，连结AO，OD，则AO =OD =MN．‎ 在Rt△ABC中，BC ＝=5．‎ ‎ 由（1）知 △AMN ∽ △ABC． ‎ ‎∴ ，即． ‎ ‎∴ ，∴ ． ‎ 过M点作MQ⊥BC 于Q，则． ‎ 在Rt△BMQ与Rt△BCA中，∠B是公共角，∴ △BMQ∽△BCA．∴ ．‎ ‎∴ ，． ∴ x＝． ‎ ‎∴ 当x＝时，⊙O与直线BC相切．‎ A B C M N P 图 3‎ O ‎（3）随点M的运动，当P点落在直线BC上时，连结AP，则O点为AP的中点．‎ ‎∵ MN∥BC，∴ ∠AMN=∠B，∠AOM＝∠APC．‎ ‎∴ △AMO ∽ △ABP． ‎ ‎∴ ． AM＝MB＝2． ‎ 故以下分两种情况讨论： ‎ ① 当0＜≤2时，． ∴ 当＝2时， ‎ ② 当2＜＜4时，设PM，PN分别交BC于E，F．‎ A B C M N P 图 4‎ O E F ‎∵ 四边形AMPN是矩形， ‎ ‎∴ PN∥AM，PN＝AM＝x． ‎ 又∵ MN∥BC， ‎ ‎∴ 四边形MBFN是平行四边形． ‎ ‎∴ FN＝BM＝4－x． ∴ ． 又△PEF ∽ △ACB． ‎ ‎∴ ．∴ ‎ ‎＝‎ 当2＜＜4时，． ‎ ‎∴ 当时，满足2＜＜4，． ‎ 综上所述，当时，值最大，最大值是2．‎ ‎40. 24．（本题满分12分）‎ B O A P M x y 如图，圆切轴于原点，过定点作圆切线交圆于点．已知，抛物线经过两点．‎ ‎（1）求圆的半径；‎ ‎（2）若抛物线经过点，求其解析式；‎ ‎（3）投抛物线交轴于点，若三角形为直角三角形，求点的坐标．‎ ‎41. 28.在平面直角坐标系中△ABC的边AB在x轴上，且OA>OB,以AB为直径的圆过点C，若C的坐标为(0,2),AB=5,‎ ‎ A,B两点的横坐标XA,XB是关于X的方程的两根:‎ (1) 求m，n的值 (2) 若∠ACB的平分线所在的直线交x轴于点D，试求直线对应的一次函数的解析式 (3) 过点D任作一直线分别交射线CA，CB（点C除外）于点M，N，则的值是否为定值，若是，求出定值，若不是，请说明理由 A C O B N D M L`‎ ‎42（08四川凉山）25．（9分）如图，在中，是的中点，以为直径的交的三边，交点分别是点．的交点为，且，．‎ ‎（1）求证：．‎ ‎（2）求的直径的长．‎ ‎（3）若，以为坐标原点，所在的直线分别为轴和轴，建立平面直角坐标系，求直线的函数表达式．‎ ‎（08四川凉山25题解析）25．（9分）‎ ‎（1）连接是圆直径，，即，．‎ ‎．在中，．‎ ‎（2）是斜边的中点，，，‎ 又由（1）知，．‎ 又，与相似 ‎ 又，‎ ‎，，‎ 设，，，直径．‎ ‎（3）斜边上中线，‎ E A D G B F C O M 第25题图 在中，，‎ 设直线的函数表达式为，‎ 根据题意得，‎ ‎ 解得 直线的函数解析式为（其他方法参照评分）‎ ‎43. 24．如图，直角坐标系中，已知两点，点在第一象限且为正三角形，的外接圆交轴的正半轴于点，过点的圆的切线交轴于点．‎ ‎（1）求两点的坐标；（2）求直线的函数解析式；‎ ‎（3）设分别是线段上的两个动点，且平分四边形的周长．试探究：的最大面积？‎ ‎（第24题）‎ ‎（第24题）‎ ‎（08浙江嘉兴24题解析）24．（1），．‎ 作于，为正三角形，，．．‎ 连，，，‎（第24题）‎ ．． ‎ ‎（2），是圆的直径，‎ 又是圆的切线，．‎ ‎，．‎ ‎．‎ 设直线的函数解析式为，‎ 则，解得．直线的函数解析式为．‎ ‎（3），，，，‎ 四边形的周长．设，的面积为，‎ 则，．‎ ‎．‎ 当时，．‎ 点分别在线段上，‎ ‎，解得．‎ 满足，‎ 的最大面积为．‎ ‎44. 08浙江宿迁）27．（本题满分12分）‎ 如图，⊙的半径为，正方形顶点坐标为，顶点在⊙上运动．‎ ‎(1)当点运动到与点、在同一条直线上时,试证明直线与⊙相切；‎ ‎(2)当直线与⊙相切时，求所在直线对应的函数关系式；‎ 第27题 ‎(3)设点的横坐标为，正方形的面积为，求与之间的函数关系式，并求出的最大值与最小值．‎ ‎45.（08山东济南24题）（本小题满分9分）‎ 已知：抛物线(a≠0)，顶点C (1，)，与x轴交于A、B两点，．‎ ‎（1）求这条抛物线的解析式．‎ ‎（2）如图，以AB为直径作圆，与抛物线交于点D，与抛物线对称轴交于点E，依次连接A、D、B、E，点P为线段AB上一个动点(P与A、B两点不重合)，过点P作PM⊥AE于M，PN⊥DB于N，请判断是否为定值? 若是，请求出此定值；若不是，请说明理由．‎ 第24题图 C O x A D P M E B N y ‎（3）在(2)的条件下，若点S是线段EP上一点，过点S作FG⊥EP ，FG分别与边AE、BE相交于点F、G(F与A、E不重合，G与E、B不重合)，请判断是否成立．若成立，请给出证明；若不成立，请说明理由．‎ ‎（08山东济南24题解析）解：(1)设抛物线的解析式为 ‎ 将A(－1，0)代入: ∴ ‎ ‎∴ 抛物线的解析式为，即：‎ ‎（2）是定值， ∵ AB为直径，∴ ∠AEB=90°，∵ PM⊥AE，∴ PM∥BE ‎∴ △APM∽△ABE，∴ ①同理: ② ‎ ‎① + ②: ‎ ‎（3）∵ 直线EC为抛物线对称轴，∴ EC垂直平分AB∴ EA=EB ‎∵ ∠AEB=90°∴ △AEB为等腰直角三角形．∴ ∠EAB=∠EBA=45° ‎ 如图，过点P作PH⊥BE于H，‎ 由已知及作法可知，四边形PHEM是矩形，‎ ‎∴PH=ME且PH∥ME 在△APM和△PBH中 ‎∵∠AMP=∠PHB=90°， ∠EAB=∠BPH=45°‎ ‎∴ PH=BH 且△APM∽△PBH ‎∴ ∴ 　①‎ 在△MEP和△EGF中，‎ ‎∵ PE⊥FG， ∴ ∠FGE+∠SEG=90°‎ ‎∵∠MEP+∠SEG=90° ∴ ∠FGE=∠MEP ‎∵ ∠PME=∠FEG=90° ∴△MEP∽△EGF ‎∴ 　　　　②由①、②知：‎ ‎46. （08四川达州23题）如图，将置于平面直角坐标系中，其中点为坐标原点，点的坐标为，．‎ ‎（1）若的外接圆与轴交于点，求点坐标．‎ ‎（2）若点的坐标为，试猜想过的直线与的外接圆的位置关系，并加以说明．‎ ‎（3）二次函数的图象经过点和且顶点在圆上，‎ 求此函数的解析式．‎ D C O A B x y F E ‎（08四川达州23题解析）解：（1）连结AD，则∠ADO＝∠B＝600‎ 在Rt△ADO中，∠ADO＝600所以OD＝OA÷＝3÷＝F 所以D点的坐标是（0，）‎ D C O A B x y ‎（2）猜想是CD与圆相切 ‎　　　∵　∠AOD是直角，所以AD是圆的直径 E 又∵　Tan∠CDO=CO/OD=1/=, ∠CDO＝300‎ ‎ ∴∠CDA=∠CDO+∠ADO=Rt∠ 即CD⊥AD ‎　∴　CD切外接圆于点D ‎（3）依题意可设二次函数的解析式为 ： ‎ y=α（x－0）(x－3)‎ 由此得顶点坐标的横坐标为：x==;‎ 即顶点在OA的垂直平分线上，作OA的垂直平分线EF，则得∠EFA＝∠B＝300‎ 得到EF＝EA＝　　　可得一个顶点坐标为（，）‎ 同理可得另一个顶点坐标为（，）‎ 分别将两顶点代入y=α（x－0）(x－3)可解得α的值分别为，‎ 则得到二次函数的解析式是y=x(x－3)或y= x(x－3)‎ ‎47.如图14，已知半径为1的与轴交于两点，为的切线，切点为，圆心的坐标为 ‎，二次函数的图象经过两点．‎ ‎（1）求二次函数的解析式；（2）求切线的函数解析式；‎ y A H F M O P1‎ P2‎ O1‎ x B 图14‎ y x O A B M O1‎ ‎（3）线段上是否存在一点，使得以为顶点的三角形与相似．若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．‎ 解：（1）圆心的坐标为，半径为1，，……1分 二次函数的图象经过点，可得方程组 解得：二次函数解析式为 ‎（2）过点作轴，垂足为．‎ 是的切线，为切点，（圆的切线垂直于经过切点的半径）．‎ 在中，‎ 为锐角，，‎ 在中，．‎ ‎．点坐标为 设切线的函数解析式为，由题意可知， 7分 切线的函数解析式为 ‎（3）存在．‎ ‎①过点作轴，与交于点．可得（两角对应相等两三角形相似）‎ ‎，‎ ‎②过点作，垂足为，过点作，垂足为．‎ 可得（两角对应相等两三角开相似）‎ 在中，，，‎ 在中，，‎ ‎，‎ 符合条件的点坐标有，‎ ‎48. （08湖南永州25题）（10分）如图，二次函数y＝ax2＋bx＋c(a＞0)与坐标轴交于点A、B、C且OA＝1，OB＝OC＝3 ．‎ ‎（1）求此二次函数的解析式．‎ ‎（2）写出顶点坐标和对称轴方程．‎ ‎（3）点M、N在y＝ax2＋bx＋c的图像上(点N在点M的右边)，且MN∥x轴，求以MN为直径且与x轴相切的圆的半径．‎ ‎（08湖南永州25题解析）（1）依题意分别代入 解方程组得所求解析式为 ‎（2）顶点坐标，对称轴 ‎（3）设圆半径为，当在轴下方时，点坐标为 把点代入得 同理可得另一种情形圆的半径为或 ‎49. （08上海市卷25题）（本题满分14分，第（1）小题满分5分，第（2）小题满分4分，第（3）小题满分5分）‎ 已知，，（如图13）．是射线上的动点（点与点不重合），是线段的中点．‎ ‎（1）设，的面积为，求关于的函数解析式，并写出函数的定义域；‎ ‎（2）如果以线段为直径的圆与以线段为直径的圆外切，求线段的长；‎ ‎（3）联结，交线段于点，如果以为顶点的三角形与相似，求线段的长．‎ B A D M E C 图13‎ B A D C 备用图 ‎（08上海市卷25题解析）解：（1）取中点，联结，‎ 为的中点，，．‎ 又，．，得；‎ ‎（2）由已知得．以线段为直径的圆与以线段为直径的圆外切，‎ ‎，即．解得，即线段的长为；‎ ‎（3）由已知，以为顶点的三角形与相似，又易证得．‎ 由此可知，另一对对应角相等有两种情况：①；②．‎ ‎①当时，，．．‎ ‎，易得．得；‎ ‎②当时，，．‎ ‎．又，．‎ ‎，即，得．‎ 解得，（舍去）．即线段的长为2．综上所述，所求线段的长为8或2．‎ ‎50. （08内蒙古赤峰25题）（本题满分14分）‎ 在平面直角坐标系中给定以下五个点．‎ ‎（1）请从五点中任选三点，求一条以平行于轴的直线为对称轴的抛物线的解析式；‎ ‎（2）求该抛物线的顶点坐标和对称轴，并画出草图；‎ y O x G F H ‎（3）已知点在抛物线的对称轴上，直线过点且垂直于对称轴．验证：以为圆心，为半径的圆与直线相切．请你进一步验证，以抛物线上的点为圆心 为半径的圆也与直线相切．由此你能猜想到怎样的结论．‎ ‎（08内蒙古赤峰25题解析）25．解：（1）设抛物线的解析式为，‎ 且过点，由在H ．则．‎ y O x F H Q M N 得方程组，‎ 解得．‎ 抛物线的解析式为 ‎（2）由 得顶点坐标为，对称轴为．‎ ‎（3）①连结，过点作直线的垂线，垂足为，‎ 则．在中，，，‎ ‎，，‎ 以点为圆心，为半径的与直线相切．‎ ‎②连结过点作直线的垂线，垂足为．过点作垂足为，‎ 则．‎ 在中，，．．‎ 以点为圆心为半径的与直线相切．‎ ‎③以抛物线上任意一点为圆心，以为半径的圆与直线相切．‎ 单纯的课本内容，并不能满足学生的需要，通过补充，达到内容的完善 ‎ 教育之通病是教用脑的人不用手，不教用手的人用脑，所以一无所能。教育革命的对策是手脑联盟，结果是手与脑的力量都可以大到不可思议。‎