2011门头沟中考一模数学试题及答案 10页

‎2011年门头沟区初三年级第一次统一练习 数 学 试 卷 ‎ 考生须知 ‎1．本试卷共6页，共五道大题，25道小题，满分120分。考试时间120分钟。‎ ‎2．在试卷和答题卡的密封线内准确填写学校、班级和姓名。‎ ‎3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。 ‎ ‎4．在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。‎ ‎5．考试结束，将本试卷、答题卡和草稿纸一并交回。‎ 一、选择题（本题共32分，每小题4分）‎ 下列各题均有四个选项，其中只有一个是符合题意的． ‎ ‎1．-6的绝对值等于 ‎ A．6 B． C． D．‎ ‎2．温家宝总理在十一届人大四次会议上所作的政府工作报告中指出，我国社会生产力、 综合国力显著提高． “十一五”期间，国民经济迈上新的台阶，国内生产总值达到398000万亿元．将398000用科学记数法表示应为 A． B． C． D．‎ ‎3．把多项式分解因式，结果正确的是 A． B． C． D．‎ ‎4．如图，在矩形ABCD中，O是对角线AC、BD的交点，‎ 点E、F分别是OD、OC的中点．如果AC=10，BC=8，‎ 那么EF的长为 A．6 B．5 ‎ C．4 D．3‎ ‎5．某学习小组的7名同学积极捐出自己的零花钱支援玉树地震灾区，他们捐款的数额分别是（单位：元）：50，20，50，30，50，40，60，则这组数据的众数和中位数分别是 A．50，50 B．50，30 C．50，20 D．60，50‎ ‎6．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，交⊙O于点D．‎ 若∠CDB=30°，⊙O的半径为，则弦CD的长是 A． B．3 C． D．9 ‎ ‎7．一个口袋中装有八个除标号不同外其它完全相同的小球，小球上分别标有数字 ，，，，，，，，从口袋中随机地摸出一个小球，则摸出的小球上的数字是偶数的概率是 A． B． C． D． ‎ ‎8．如图1是一个小正方体的平面展开图，小正方体从图2所示的位置依次翻到第1格、第2格、第3格，这时小正方体朝上一面的字是 ‎ 设 生 态 家 园 图1‎ 建 ‎ ‎ 图2‎ ‎ ‎ ‎ A．生 B．态 C．家 D．园 二、填空题（本题共16分，每小题4分）‎ ‎9． 在函数中，自变量x的取值范围是 ．‎ ‎10．若，则m－n的值为 ．‎ ‎11．将二次函数化为的形式，则y= ．‎ ‎12．已知一个面积为S的等边三角形，现将其各边n（n为大于2的整数）等分，并以相邻等分点为顶点向外作小等边三角形（如图所示）．‎ n=3‎ n=5‎ ‎……‎ n=4‎ 当n = 8时，共向外作出了 个小等边三角形； 当n = k时，共向外作出了 个小等边三角形，这些小等边三角形的面积和是 （用 含k的式子表示）．‎ 三、解答题（本题共30分，每小题5分）‎ ‎13．计算：．‎ A Ｂ Ｃ F E D ‎14．解分式方程 ．　　‎ ‎ ‎ ‎15．已知：如图，EF∥BC，点F、点C在AD上， AF=DC， EF=BC．‎ 求证：AB=DE．‎ ‎16．已知，求代数式的值． ‎ ‎17．列方程或方程组解应用题：‎ ‎ “地球一小时”是世界自然基金会在2007年提出的一项倡议．号召个人、社区、企业和政府在每年3月最后一个星期六20时30分—21时30分熄灯一小时，旨在通过一个人人可为的活动，让全球民众共同携手关注气候变化，倡导低碳生活．中国内地去年和今年共有119个城市参加了此项活动，且今年参加活动的城市个数比去年的3倍少13个，问中国内地去年、今年分别有多少个城市参加了此项活动． ‎ ‎·‎ A B O x y ‎1‎ ‎1‎ ‎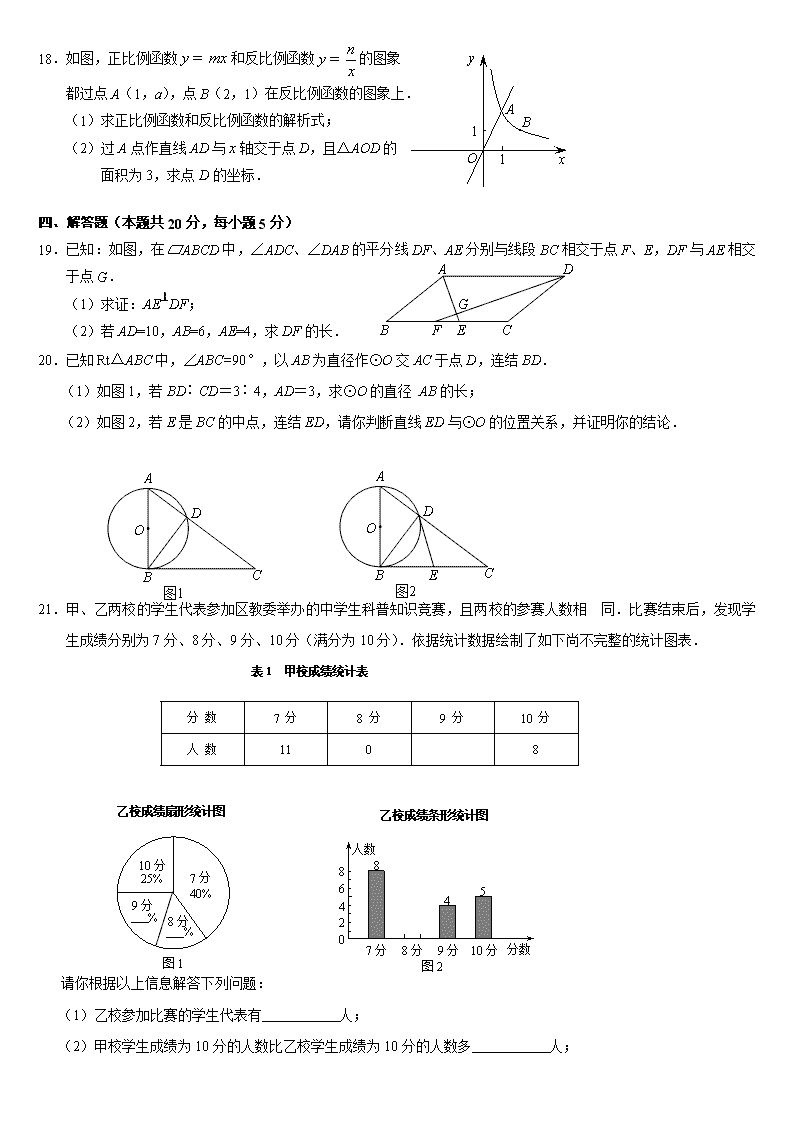18．如图，正比例函数和反比例函数的图象 都过点A（1，a），点B（2，1）在反比例函数的图象上．‎ ‎（1）求正比例函数和反比例函数的解析式；‎ ‎（2）过A点作直线AD与轴交于点D，且△AOD的 面积为3，求点D的坐标． ‎ 四、解答题（本题共20分，每小题5分） ‎ ‎19．已知：如图，在□ABCD中，∠ADC、∠DAB的平分线DF、AE分别与线段BC相交于点F、E，DF与AE相交于点G．‎ ‎（1）求证：AE⊥DF；‎ ‎（2）若AD=10，AB=6，AE=4，求DF的长．‎ ‎20．已知Rt△ABC中，∠ABC=90°，以AB为直径作⊙O交AC于点D，连结BD．‎ ‎（1）如图1，若BD∶CD＝3∶4，AD＝3，求⊙O的直径 AB的长；‎ ‎（2）如图2，若E是BC的中点，连结ED，请你判断直线ED与⊙O的位置关系，并证明你的结论．‎ ‎21．甲、乙两校的学生代表参加区教委举办的中学生科普知识竞赛，且两校的参赛人数相 同．比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）．依据统计数据绘制了如下尚不完整的统计图表．‎ 表1 甲校成绩统计表 分 数 ‎7 分 ‎8 分 ‎9 分 ‎10 分 人 数 ‎11‎ ‎0‎ ‎8‎ ‎ ‎ 乙校成绩扇形统计图 ‎ 乙校成绩条形统计图 ‎2‎ ‎8‎ ‎6‎ ‎4‎ ‎8分 ‎9分 人数 ‎2‎ ‎10分 ‎7分 ‎0‎ ‎8‎ ‎4‎ ‎5‎ ‎ ‎ ‎10分 ‎25%‎ ‎40%‎ ‎7分 ‎7分 分数 ‎9分 ‎8分 ‎ %‎ ‎ %‎ ‎7分 图1‎ 图2 ‎ 请你根据以上信息解答下列问题：‎ ‎（1）乙校参加比赛的学生代表有 人；‎ ‎（2）甲校学生成绩为10分的人数比乙校学生成绩为10分的人数多 人； ‎ ‎（3）请你将表1、图1和图2补充完整．‎ ‎22．已知正方形ABCD的边长AB=k（k是正整数），等边三角形PAE的顶点P在正方形内，顶点E在边AB上，且AE=1. 将等边三角形PAE在正方形内按图1中所示的方式，沿着正方形的边AB、BC、CD、DA、AB、…连续地翻转n次，使顶点P第一次回到原来的起始位置.‎ ‎（1）如果我们把正方形ABCD的边展开在一条直线上，那么这一翻转过程可以看作是等边三角形PAE在直线上作连续的翻转运动. 图2是k=1时，等边三角形PAE沿正方形的边连续翻转过程的展开示意图．请你探索：若k=1，则等边三角形PAE沿正方形的边连续翻转的次数n= 时, 顶点P第一次回到原来的起始位置.‎ ‎（2）若k=3，则等边三角形PAE沿正方形的边连续翻转的次数n= 时，顶点P第一次回到原来的起始位置；‎ ‎（3）使顶点P第一次回到原来的起始位置时，若等边三角形PAE沿正方形的边连续翻转的次数是60，则正方形ABCD的边长AB= .‎ 五、解答题（本题共22分，第23、24题各7分，第25题8分） ‎ ‎23．已知关于 的一元二次方程．‎ ‎（1）若此一元二次方程有实数根，求m的取值范围；‎ ‎（2）若关于x的二次函数和的图象都经过x轴上的点（n，0），求m的值；‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ x y O ‎-1‎ ‎-2‎ ‎-3‎ ‎-4‎ ‎-4‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎（3）在（2）的条件下，将二次函数的图象先沿x轴翻折，再向下平移3个单位，得到一个新的二次函数的图象．请你直接写出二次函数的解析式，并结合函数的图象回答：当x取何值时，这个新的二次函数的值大于二次函数的值．‎ ‎24．在梯形ABCD中，AD∥BC, ∠ABC =90°，且AD=1，AB=2，tan∠DCB=2 ，对角线AC和BD相交于点O．在等腰直角三角形纸片EBF中，∠EBF=90°，EB=FB．把梯形ABCD固定不动，将三角形纸片EBF绕点B旋转．‎ ‎（1）如图1，当三角形纸片EBF绕点B旋转到使一边BF与梯形ABCD的边BC在同一条直线上时，线段AF与CE的位置关系是 ，数量关系是 ；‎ ‎（2） 将图1中的三角形纸片EBF绕点B逆时针继续旋转, 旋转角为（）,请你在图2 中画出图形，并判断（1）中的两个结论是否发生变化，写出你的猜想并加以证明；‎ ‎（3）将图1中的三角形纸片EBF绕点B逆时针旋转到一边BF恰好落在线段BO上时,‎ 三角形纸片EBF的另一边EF与BC交于点M，请你在图3中画出图形．‎ ‎①判断（1）中的两个结论是否发生变化，直接写出你的猜想，不必证明；‎ ‎②若，求BM的长． ‎ ‎ 25．在平面直角坐标系xOy中，关于y轴对称的抛物线 与x轴交于A、B 两点（点A在点B的左侧），与y轴交于点C，P是这条抛物线上的一点（点P不在坐标轴上），且点P关于直线BC的对称点在x轴上，D（0，3）是y轴上的一点．‎ ‎（1）求抛物线的解析式及点P的坐标； ‎ ‎（2）若E、F是 y 轴负半轴上的两个动点（点E ‎ 在点F的上面），且EF＝2，当四边形PBEF 的周长最小时，求点E、F的坐标；‎ ‎（3）若Q是线段AC上一点,且，‎ M是直线DQ上的一个动点，在x轴上方的 平面内存在一点N，使得以 O、D、M、N ‎ 为顶点的四边形是菱形，请你直接写出点N 的坐标．‎ ‎2011年门头沟区初三年级第一次统一练习 数学试卷评分参考 一、选择题（本题共32分，每小题4分） ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 A ‎ D C ‎ D A ‎ B ‎ C ‎ D 二、填空题（本题共16分，每小题4分）‎ 题号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 ‎5‎ ‎18‎ 三、解答题（本题共30分，每小题5分）‎ ‎13．计算：．‎ ‎ 解： ‎ ‎= ……………………………………………………………………4分 ‎= ． ……………………………………………………………………………5分 ‎14．解分式方程 ．‎ 解：去分母，得 ． ……………………………………2分 整理，得 ．‎ 解得 ． ……………………………………………………………………4分 经检验，是原方程的解．‎ 所以原方程的解是． ………………………………………………………5分 ‎15． 证明：∵， ‎ ‎ ∴． …………………………1分 ‎ A Ｂ Ｃ F E D ‎ ，‎ ‎ ∴． …………………2分 ‎ 在△与△中，‎ ‎ ‎ ‎ ∴． ……………………………………………………4分 ‎ ∴AB=DE． ……………………………………………………………………5分 ‎16． 解： ‎ ‎ …………………………………………2分 ‎ ………………………………………………… 3分 ‎． ……………………………………………………………………………4分 当时，原式． …………………………………………………… 5分 ‎17．解：设中国内地去年有x个城市参加了此项活动，今年有y个城市参加了此项活动．…1分 ‎ 依题意，得 ………………………………………………………………3分 ‎ 解得 ………………………………………………………………………4分 ‎ 答：去年有33个城市参加了此项活动，今年有86个城市参加了此项活动． …………5分 Ｂ O Ｄ１‎ x y ‎1‎ ‎1‎ A ‎．‎ Ｄ２‎ ‎18. 解：（1）∵反比例函数的图象经过点B（2，1）,‎ ‎ ∴．‎ ‎ ∴反比例函数的解析式是． …………1分 ‎ 点A（1，a）在反比例函数的图象上，‎ ‎ ∴．‎ ‎ ∴．……………………………………2分 ‎ ∵正比例函数的图象经过点，‎ ‎ ∴ ． ‎ ‎ ∴正比例函数的解析式是．………………………………………………3分 ‎ （2）依题意，得． ‎ ‎ ∴． ‎ ‎ ∴ D点坐标为或． ……………………………………………5分 四、解答题（本题共20分，每小题5分）‎ ‎19. 解：（1）在□ABCD中，， ‎ ‎∴∠ADC+∠DAB=180°．‎ DF、AE分别是∠ADC、∠DAB的平分线，‎ ‎∴，． ‎ ‎∴．‎ ‎∴．‎ ‎∴AE⊥DF．…………………………………………………………………………2分 ‎（2）过点D作，交BC的延长线于点H，‎ 则四边形AEHD是平行四边形，且FD⊥DH．‎ ‎∴DH=AE=4，EH=AD=10. ‎ 在□ABCD中，，‎ ‎∴∠ADF=∠CFD，∠DAE=∠BEA．‎ ‎∴∠CDF=∠CFD，∠BAE=∠BEA．‎ ‎∴DC=FC，AB=EB．‎ 在□ABCD中，AD=BC=10，AB=DC=6，‎ ‎∴CF=BE=6，BF=BC－CF=10－6=4．‎ ‎∴FE=BE－BF=6－4=2． …………………………………………………………3分 ‎∴FH= FE+EH= 12． ………………………………………………………………4分 在Rt△FDH中，.………………………………5分 ‎20．解：（1）如图1，∵ AB是⊙O的直径，‎ ‎∴ ∠ADB=90°． ‎ 则∠CDB=∠ADB=90°．‎ 图1‎ A C B D O ‎·‎ ‎∴∠C+∠CBD=90°．‎ ‎∵∠ABC=90°，‎ ‎∴∠ABD+∠CBD=90°．‎ ‎∴∠C=∠ABD．‎ ‎∴△ADB∽△BDC．‎ ‎∴．‎ ‎∵BD：CD =3：4，AD=3， ‎ ‎∴BD=4．‎ 在Rt△ABD中，． …………………………3分 ‎（2）直线ED与⊙O相切． ‎ 图2‎ A C B D E O ‎·‎ 证明：如图2，连结OD．‎ ‎ 由（1）得∠BDC=90°．‎ ‎ ∵E是BC的中点， ‎ ‎ ∴DE=BE．‎ ‎∴∠EDB=∠EBD．‎ ‎∵OB=OD，‎ ‎∴∠ODB=∠OBD．‎ ‎∵∠OBD+∠EBD=90°，‎ ‎∴∠ODB+∠EDB=∠ODE=90°． ‎ ‎∴ED是⊙O的切线．　……………………………………………………………5分 ‎21．解：（1）20． ……………………………………………………………………………1分 ‎ ‎ （2）3． ………………………………………………………………………………2分 ‎ （3）补全表1、图1和图2． ……………………………………………………5分 ‎22．解：（1）12． …………………………………………………………………………………2分图1‎ 图2‎ 图3‎ ‎ （2）12． ………………………………………………………………………………3分 ‎ （3）5或15. ……………………………………………………………………………5分 五、解答题（本题共22分，第23、24题各7分，第25题8分）‎ ‎23．解：（1）根据题意，得 解得 ‎ ∴m的取值范围是m≥－3且m≠－2．…………………………………………2分 ‎（2）关于x的二次函数和的图象都经过x轴上的点（n，0），‎ ‎ ∴．‎ ‎ 解得n=－1． ………………………………………………………………………3分 当n=－1时，， ‎ 解得m=－3． …………………………………………………………………4分 ‎（3）． …………………………………………………………………5分 当x的取值范围是或时，二次函数的值大于二次函数的值．‎ ‎ …………………………………………………………7分 ‎ ‎24．解：（1）垂直，相等 ……………………………………………………………………2分 ‎（2）猜想：（1）中的两个结论没有发生变化． ‎ ‎ 证明：如图2，过D作于G．‎ ‎ ∵，‎ ‎　　　　　　∴DG∥AB.‎ ‎　　　　　　∵AD∥BC，‎ ‎∴四边形ABGD为矩形.‎ ‎ ∴AB=DG=2,AD=BG=1. ‎ ‎∵tan∠DCB==2,‎ ‎∴.‎ ‎∴ CB = AB =2.‎ ‎∵，‎ ‎∴.‎ ‎∴.‎ 在△ABF和△CBE中，‎ ‎∴△ABF≌△CBE.‎ ‎∴.‎ ‎∵，，‎ ‎∴.‎ ‎∴.‎ ‎ ………………………………………………………………4分 M ‎（3）①猜想：（1）中的两个结论没有发生变化．‎ ‎②如图3，AD∥BC， ‎ ‎∴△AOD∽△COB．‎ ‎∴．‎ AD＝1，BC＝2，‎ ‎∴．‎ 在Rt△DAB中，．‎ ‎∴．‎ ‎∵,‎ ‎ ∴．‎ ‎∠1＋∠FBM=90°，∠2＋∠FBM=90°,‎ ‎．‎ 又 ‎∴△BME∽△BOA.‎ ‎∴ ‎ ‎∴‎ ‎∴ ………………………………………………………………………7分 ‎25. 解：（1）∵抛物线关于y轴对称,‎ ‎∴m－2=0．‎ ‎∴m=2．‎ ‎∴抛物线的解析式是.………………………………………………2分 令y＝0，得.‎ ‎∴，．‎ 在Rt△中，OC＝1, OB＝,可得∠OBC＝30º.‎ 在Rt△中，OD＝3, OB＝,可得∠OBD＝60º.‎ ‎∴BC是∠OBD的角平分线.‎ ‎∴直线BD与x轴关于直线BC对称.‎ 因为点P关于直线BC的对称点在x轴上，‎ 则符合条件的点P就是直线BD与抛物线 的交点.‎ 设直线BD的解析式为.‎ ‎∴ ∴‎ ‎∴直线BD的解析式为.‎ ‎∵点P在直线BD上，设P点坐标为.‎ 又因为点P 在抛物线上，‎ ‎∴.‎ 解得.‎ ‎∴.‎ ‎∴点P的坐标是.……………………………………………………………3分 ‎（2）过点P作PG⊥ 轴于G，在PG上截取，连结AH与轴交于点，在轴的负半轴上截取.‎ x y G H E F ‎-1‎ D ‎∵ PH∥EF，，‎ ‎∴ 四边形为平行四边形，有.‎ 又 ∵ 、的长为定值，‎ ‎∴ 此时得到的点、使四边形的周长最小. ‎ ‎∵ OE∥GH，‎ ‎∴ Rt△∽Rt△.‎ ‎∴ .‎ ‎∴ .‎ ‎∴ .‎ ‎∴ 点的坐标为（0，），点的坐标为（0，）. …………………………5分 ‎（3）点N的坐标是或或.………………8分