浙江省2010年初中毕业生学业考试(金华卷)数学试卷 8页

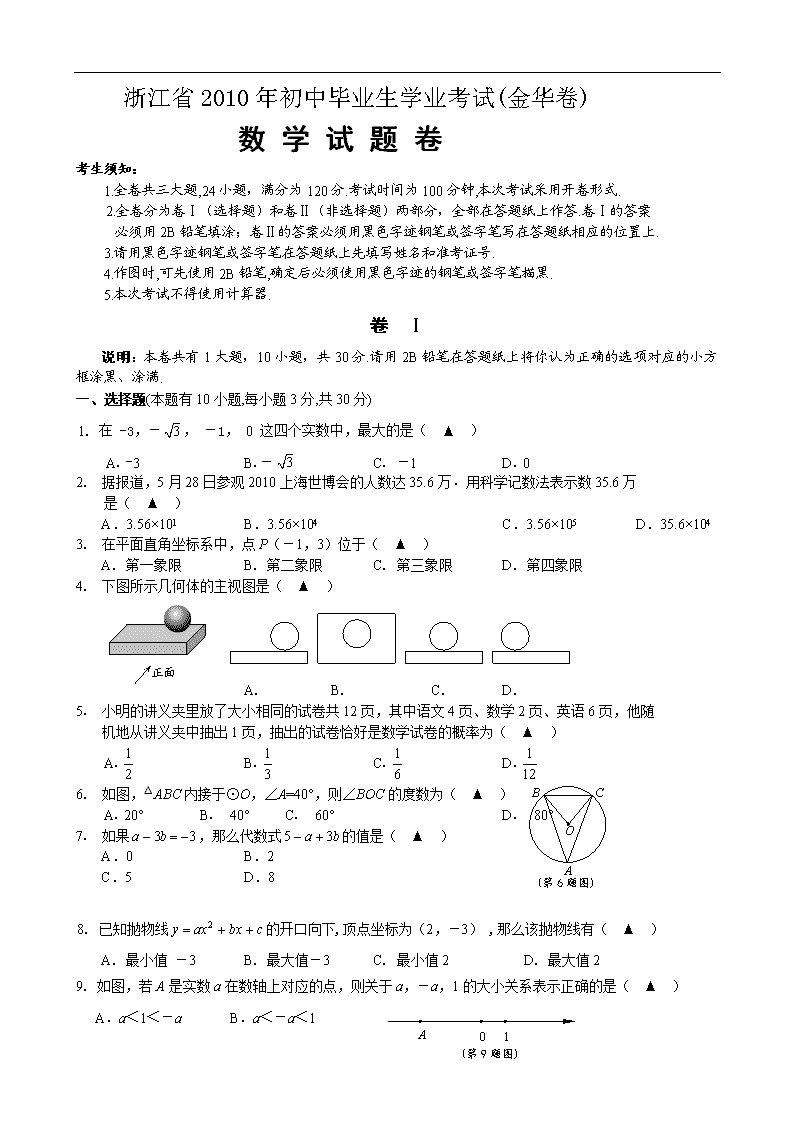
浙江省2010年初中毕业生学业考试(金华卷)‎ ‎ 数 学 试 题 卷 考生须知：‎ ‎1.全卷共三大题,24小题，满分为120分.考试时间为100分钟,本次考试采用开卷形式.‎ ‎2.全卷分为卷Ⅰ（选择题）和卷Ⅱ（非选择题）两部分，全部在答题纸上作答.卷Ⅰ的答案 必须用2B铅笔填涂；卷Ⅱ的答案必须用黑色字迹钢笔或签字笔写在答题纸相应的位置上.‎ ‎3.请用黑色字迹钢笔或签字笔在答题纸上先填写姓名和准考证号.‎ ‎4.作图时,可先使用2B铅笔,确定后必须使用黑色字迹的钢笔或签字笔描黑.‎ ‎5.本次考试不得使用计算器.‎ 卷 Ⅰ ‎ 说明：本卷共有1大题，10小题，共30分.请用2B铅笔在答题纸上将你认为正确的选项对应的小方框涂黑、涂满.‎ 一、选择题(本题有10小题,每小题3分,共30分)‎ ‎1. 在 -3，－， －1， 0 这四个实数中，最大的是（ ▲ ） ‎ A. -3 B.－ C. －1 D. 0‎ ‎2. 据报道，‎5月28日参观2010上海世博会的人数达35.6万﹒用科学记数法表示数35.6万 是（ ▲ ）‎ ‎ A．3.56×101 B．3.56×‎104 ‎ C．3.56×105 D．35.6×104 ‎ ‎3. 在平面直角坐标系中，点P（－1，3）位于（ ▲ ）‎ ‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 ‎4. 下图所示几何体的主视图是（ ▲ ）‎ 正面 ‎ ‎ ‎ A. B. C. D. ‎ ‎5. 小明的讲义夹里放了大小相同的试卷共12页，其中语文4页、数学2页、英语6页，他随 ‎ 机地从讲义夹中抽出1页，抽出的试卷恰好是数学试卷的概率为（ ▲ ）‎ ‎(第6题图) ‎ A C B O ‎ A. B. C. D.‎ ‎6. 如图，△ABC内接于⊙O，∠A=40°，则∠BOC的度数为（ ▲ ）‎ ‎ A. 20° B. 40° C. 60° D. 80° ‎ ‎7. 如果，那么代数式的值是（ ▲ ）‎ ‎ A．0 B．2‎ ‎ C．5 D．8‎ ‎ 8. 已知抛物线的开口向下,顶点坐标为（2，－3） ,那么该抛物线有（ ▲ ）‎ ‎ A. 最小值 －3 B. 最大值－‎3 ‎ C. 最小值2 D. 最大值2‎ ‎9. 如图，若A是实数a在数轴上对应的点，则关于a，－a，1的大小关系表示正确的是（ ▲ ）‎ ‎0‎ ‎1‎ A ‎(第9题图)‎ A．a＜1＜－a B．a＜－a＜1 ‎ C．1＜－a＜a D．－a＜a＜1‎ ‎10. 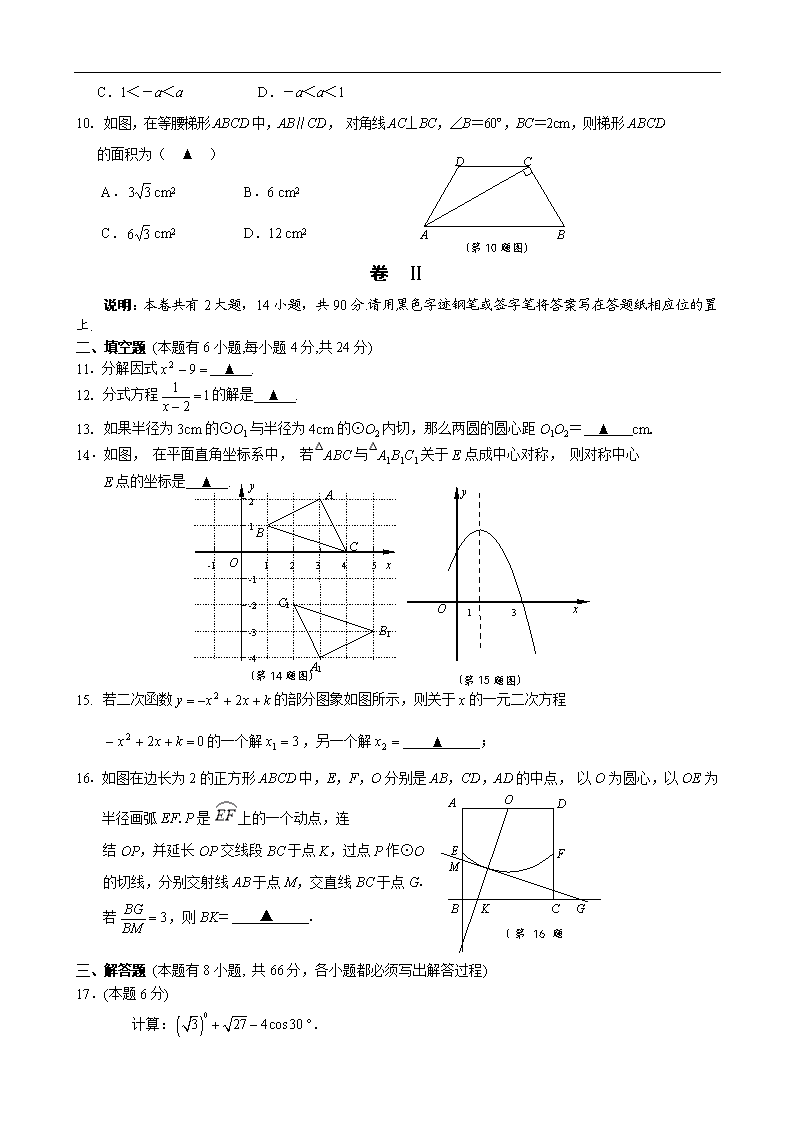如图，在等腰梯形ABCD中，AB∥CD， 对角线AC⊥BC，∠B＝60º，BC＝‎2cm，则梯形ABCD A C B D ‎(第10题图)‎ 的面积为（ ▲ ）‎ ‎ A．cm2 B．‎6 cm2 ‎ ‎ C．cm2 D．‎12 cm2‎ 卷 Ⅱ 说明：本卷共有2大题，14小题，共90分.请用黑色字迹钢笔或签字笔将答案写在答题纸相应位的置上.‎ 二、填空题 (本题有6小题,每小题4分,共24分)‎ ‎11. 分解因式 ▲ .‎ ‎12. 分式方程的解是 ▲ . ‎ ‎13. 如果半径为‎3cm的⊙O1与半径为‎4cm的⊙O2内切，那么两圆的圆心距O1O2＝ ▲ cm.‎ ‎14﹒如图， 在平面直角坐标系中， 若△ABC与△A1B‎1C1关于E点成中心对称， 则对称中心 ‎(第14题图)‎ A O x y ‎1‎ ‎2‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-1‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎-4‎ B C A1‎ C1‎ B1‎ ‎5‎ y ‎(第15题图)‎ O x ‎1‎ ‎3‎ E点的坐标是 ▲ . ‎ ‎ ‎ 15. 若二次函数的部分图象如图所示，则关于x的一元二次方程 的一个解，另一个解 ▲ ；‎ A O D B F K E ‎(第16题图)‎ G M CK ‎16. 如图在边长为2的正方形ABCD中，E，F，O分别是AB，CD，AD的中点， 以O为圆心，以OE为半径画弧EF.P是上的一个动点，连 结OP，并延长OP交线段BC于点K，过点P作⊙O 的切线，分别交射线AB于点M，交直线BC于点G. ‎ 若，则BK﹦ ▲ .‎ 三、解答题 (本题有8小题, 共66分，各小题都必须写出解答过程)‎ ‎17．(本题6分) ‎ 计算：°．‎ ‎18．(本题6分)‎ A C B D F E ‎(第18题图)‎ 如图，在△ABC中，D是BC边上的点（不与B，C重合），F，E分别是AD及其延长线上的点，CF∥BE. 请你添加一个条件，使△BDE≌△CDF (不再添加其它线段，不再标注或使用其他字母)，并给出证明．‎ ‎（1）你添加的条件是： ▲ ；‎ ‎（2）证明： ‎ ‎19．(本题6分)‎ A B ‎45°‎ ‎60°‎ C E D ‎(第19题图)‎ 在一个阳光明媚、清风徐来的周末，小明和小强一起到郊外放风筝﹒他们把风筝放飞后，将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线（线段AC）长‎20m，风筝B的引线（线段BC）长‎24m，在C处测得风筝A的仰角为60°，风筝B的仰角为45°.‎ ‎ （1）试通过计算，比较风筝A与风筝B谁离地面更高？‎ ‎（2）求风筝A与风筝B的水平距离.‎ ‎ (精确到‎0.01 m；参考数据：sin45°≈0.707,cos45°≈0.707,‎ tan45°=1,sin60°≈0.866,cos60°=0.5,tan60°≈1.732）‎ ‎20．(本题8分)‎ ‎ 已知二次函数y=ax2＋bx－3的图象经过点A（2，－3），B（－1，0）． ‎ ‎（1）求二次函数的解析式；‎ ‎（2）填空：要使该二次函数的图象与x轴只有一个交点，应把图象沿y轴向上平移 ‎ ▲ 个单位． ‎ ‎ ‎ ‎ 21．(本题8分)‎ A C B D ‎(第21题图)‎ E F O 如图，AB是⊙O的直径，C是的中点，CE⊥AB于 E，BD交CE于点F．‎ ‎1‎ ‎2‎ ‎（1）求证：CF﹦BF；‎ ‎（2）若CD ﹦6， AC ﹦8，则⊙O的半径为 ▲ ， ‎ CE的长是 ▲ ．‎ ‎22． (本题10分)‎ ‎ 一方有难，八方支援．‎2010年4月14日青海玉树发生7.1级强烈地震，给玉树人民 造成了巨大的损失﹒灾难发生后，实验中学举行了爱心捐款活动，全校同学纷纷拿出自己 的零花钱， 踊跃捐款支援灾区人民﹒小慧对捐款情况进行了抽样调查，抽取了40名同学 ‎40名同学捐款的频数分布直方图 人数 捐款数（元）‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎30‎ O ‎(第22题图)‎ 的捐款数据，把数据进行分组、列频数分布表后，绘制了频数分布直方图．图中从左到右各长方形 高度之比为3∶4∶5∶7∶1（如图）．‎ ‎（1）捐款20元这一组的频数是 ▲ ；‎ ‎（2）40名同学捐款数据的中位数是 ▲ ；‎ ‎ （3）若该校捐款金额不少于34500 元，请估算 该校捐款同学的人数至少有多少名？‎ ‎23. (本题10分）‎ 已知点P的坐标为（m，0），在x轴上存在点Q（不与P点重合），以PQ为边作正方形PQMN，使点M落在反比例函数y = 的图像上.小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点M1在第二象限.‎ y P Q M N O x ‎1‎ ‎2‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎1‎ ‎2‎ ‎3‎ ‎(第23题图)‎ ‎（1）如图所示，若反比例函数解析式为y= ，P点坐标为（1， 0），图中已画出一符合条件的一个正方形PQMN，请你在图中画出符合条件的另一个正方形PQ‎1M1N1，并写出点M1的坐标； ‎ ‎（温馨提示：作图时，别忘 了用黑色字迹的钢笔或签字 笔描黑喔！）‎ M1的坐标是 ▲ ‎ ‎ （2） 请你通过改变P点坐标，对直线M‎1 M的解析式y﹦kx＋b进行探究可得 k﹦ ▲ ， 若点P的坐标为（m，0）时，则b﹦ ▲ ；‎ ‎ （3） 依据(2)的规律，如果点P的坐标为（6，0），请你求出点M1和点M的坐标．24. (本题12分)‎ ‎ 如图，把含有30°角的三角板ABO置入平面直角坐标系中，A，B两点坐标分别为 ‎（3，0）和(0，3）.动点P从A点开始沿折线AO-OB-BA运动，点P在AO，OB，‎ BA上运动的 面四民﹒数学兴趣小组对捐款情况进行了抽样调查，速度分别为1，，2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开 始以 (长度单位/秒)的速度向上平行移动（即移动过程中保持l∥x轴），且分别与OB，‎ AB交于E，F两点﹒设动点P与动直线l同时出发，运动时间为t秒，当点P沿折线 AO-OB-BA运动一周时，直线l和动点P同时停止运动．‎ ‎ 请解答下列问题：‎ ‎ （1）过A，B两点的直线解析式是 ▲ ；‎ ‎（2）当t﹦4时，点P的坐标为 ▲ ；当t ﹦ ▲ ，点P与点E重合； ‎ ‎ （3）① 作点P关于直线EF的对称点P′. 在运动过程中，若形成的四边形PEP′F为 ‎ 菱形，则t的值是多少？‎ ‎② 当t﹦2时，是否存在着点Q，使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标；‎ B F A P E O x y ‎(第24题图)‎ 若不存在，请说明理由．‎ 浙江省2010年初中毕业生学业考试(金华卷)‎ ‎ 数学卷参考答案及评分标准 一、 选择题（本题共10小题，每小题3分，共30分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 D C B A C D D B A A 评分标准 选对一题给3分，不选，多选，错选均不给分 二、填空题（本题有6小题，每小题4分，共24分）‎ ‎11．(x-3)(x+3)； 12.x=3； 13. 1； 14.（3，-1）； 15. -1； ‎ ‎16. , .（每个2分）‎ 三、解答题（本题有8小题，共66分）‎ ‎17. (本题6分) ‎ ‎ 解：原式﹦1＋－…………5分（三式化简对1个2分，对2个4分，对3个5分）‎ ‎ ﹦1＋．……………………………………………………………………………1分 A C B D F E ‎18．(本题6分)‎ ‎ 解：（1）(或点D是线段BC的中点)，，中 任选一个即可﹒………………………………2分 ‎（2）以为例进行证明：‎ ‎∵CF∥BE， ‎ ‎∴∠FCD﹦∠EBD．‎ ‎ 又∵，∠FDC﹦∠EDB，‎ A B ‎45°‎ ‎60°‎ C E D ‎ ∴△BDE≌△CDF．…………………4分 ‎19．(本题6分)‎ ‎ 解：（1）分别过A，B作地面的垂线，垂足分别为D，E．‎ ‎ 在Rt△ADC中，‎ ‎∵AC﹦20，∠ACD﹦60°，‎ ‎∴AD﹦20×sin 60°﹦10≈‎‎17.32m ‎ 在Rt△BEC中，‎ ‎∵BC﹦24，∠BEC﹦45°，‎ ‎∴BE﹦24×sin 45°﹦12≈16.97 ‎ ‎ ∵17.32>16.97‎ ‎ ∴风筝A比风筝B离地面更高． ………………………………………………………3分 ‎ （2）在Rt△ADC中，‎ ‎∵AC﹦20，∠ACD﹦60°，‎ ‎∴DC﹦20×cos 60°﹦‎‎10 m ‎ 在Rt△BEC中，‎ ‎∵BC﹦24，∠BEC﹦45°，∴EC﹦BC≈‎‎16.97 m ‎ ∴EC－DC≈16.97－10﹦‎‎6.97m ‎ 即风筝A与风筝B的水平距离约为‎6.97m．…………………………………………3分 ‎20. (本题8分)‎ ‎ 解：(1)由已知，有，即，解得 ‎∴所求的二次函数的解析式为. …………………………………………6分 ‎(2) 4 …………………………………………………………………………………………2分 A C B D E F O ‎1‎ ‎2‎ ‎21. (本题8分)‎ ‎ 解：(1) 证明：∵AB是⊙O的直径，∴∠ACB﹦90°‎ ‎ 又∵CE⊥AB， ∴∠CEB﹦90°‎ ‎ ∴∠2﹦90°－∠A﹦∠1‎ ‎ 又∵C是弧BD的中点，∴∠1﹦∠A ‎ ∴∠1﹦∠2,‎ ‎ ∴ CF﹦BF﹒ …………………4分 ‎40名同学捐款情况统计图 人数 捐款数（元）‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎30‎ O ‎(2) ⊙O的半径为5 ， CE的长是﹒ ………4分（各2分）‎ ‎22．(本题10分)‎ ‎ 解：（1）14 ………3分 （2）15 …………3分 ‎ (3) 设该校捐款的同学有x人 ‎ 由题意得 15x≥ 34500‎ ‎ 解得 x ≥2300‎ 答：该校捐款的同学至少有2300人． ……4分 M1‎ P Q M N O y ‎1‎ ‎2‎ ‎3‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎1‎ ‎2‎ ‎3‎ Q1‎ N1‎ ‎23．(本题10分)‎ ‎ 解：（1）如图；M1 的坐标为（－1，2） ……2分 ‎ （2）， …………………4分（各2分）‎ ‎ （3）由（2）知，直线M‎1 M的解析式为 x ‎ 则(，)满足 ‎ 解得 ，‎ ‎ ∴ ，‎ ‎ ∴M1，M的坐标分别为（，），（，）．……………4分 ‎24．(本题12分)‎ B F A P E O x y G P′‎ P′‎ ‎(图1)‎ ‎ 解：（1）；………4分 （2）（0,），；……4分（各2分）‎ ‎ （3）①当点在线段上时，过作⊥轴，为垂足（如图1）‎ ‎ ∵,,∠∠90°‎ ‎ ∴△≌△，∴﹒‎ 又∵,∠60°,∴‎ ‎ 而，∴,‎ B F A P E O x y M P′‎ H ‎（图2)‎ ‎ 由得 ；………………………………………………………………1分 ‎ 当点P在线段上时，形成的是三角形，不存在菱形；‎ ‎ 当点P在线段上时，‎ 过P作⊥，⊥，、分别为垂足（如图2）‎ ‎ ∵,∴,∴‎ ‎ ∴， 又∵‎ ‎ 在Rt△中，‎ ‎ 即，解得．…………………………………………………1分 B F A P E O x Q′‎ B′‎ Q C C1‎ D1‎ ‎(图3)‎ y ‎②存在﹒理由如下：‎ ‎ ∵，∴,，‎ 将△绕点顺时针方向旋转90°，得到 ‎△（如图3）‎ ‎ ∵⊥，∴点在直线上，‎ ‎ C点坐标为（，－1）‎ ‎ 过作∥，交于点Q,‎ 则△∽△‎ ‎ 由，可得Q的坐标为（－，）………………………1分 根据对称性可得，Q关于直线EF的对称点（－，）也符合条件．……1分