2011湖南衡阳中考数学 11页

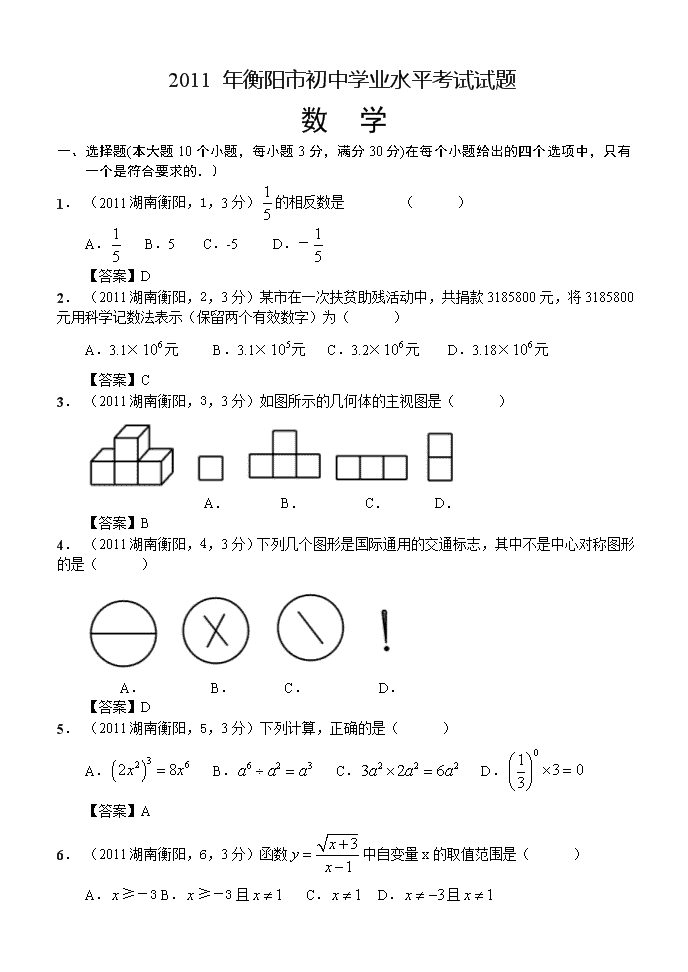
‎2011 年衡阳市初中学业水平考试试题 数 学 一、选择题(本大题10个小题，每小题3分，满分30分)在每个小题给出的四个选项中，只有一个是符合要求的．）‎ ‎1． （2011湖南衡阳，1，3分）的相反数是 （ ）‎ A． B．‎5 ‎‎ C．-5 D．－‎ ‎【答案】D ‎2． （2011湖南衡阳，2，3分）某市在一次扶贫助残活动中，共捐款3185800元，将3185800元用科学记数法表示（保留两个有效数字）为（ ）‎ A．3.1×元 B．3.1×元 C．3.2×元 D．3.18×元 ‎【答案】C ‎3． （2011湖南衡阳，3，3分）如图所示的几何体的主视图是（ ）‎ ‎ ‎ A． B． C． D． ‎ ‎【答案】B ‎4． （2011湖南衡阳，4，3分）下列几个图形是国际通用的交通标志，其中不是中心对称图形的是（ ）‎ ‎ ‎ A． B． C． D． ‎ ‎【答案】D ‎5． （2011湖南衡阳，5，3分）下列计算，正确的是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎6． （2011湖南衡阳，6，3分）函数中自变量x的取值范围是（ ）‎ A．≥－3 B．≥－3且 C． D．且 ‎【答案】B ‎7． （2011湖南衡阳，7，3分）下列说法正确的是（ ）‎ A．在一次抽奖活动中，“中奖的概率是”表示抽奖100次就一定会中奖 B．随机抛一枚硬币，落地后正面一定朝上 C．同时掷两枚均匀的骰子，朝上一面的点数和为6‎ D．在一副没有大小王的扑克牌中任意抽一张，抽到的牌是6的概率是 ‎【答案】D ‎8． （2011湖南衡阳，8，3分）如图所示，在平面直角坐标系中，菱形MNPO的顶点P坐标是（3，4），则顶点M、N的坐标分别是（ ）‎ A．M(5，0)，N(8，4) B．M(4，0)，N(8，4)‎ C．M(5，0)，N(7，4) D．M(4，0)，N(7，4)‎ ‎【答案】A ‎9． （2011湖南衡阳，9，3分）如图所示，河堤横断面迎水坡AB的坡比是1：，堤高BC=‎5m，则坡面AB的长度是（ ）‎ A．‎10m B．‎10‎m C．‎15m D．‎5‎m ‎ ‎【答案】A ‎10．（2011湖南衡阳，10，3分）某村计划新修水渠‎3600米，为了让水渠尽快投入使用，实际工作效率是原计划工作效率的1.8倍，结果提前20天完成任务，若设原计划每天修水渠米，则下面所列方程正确的是（ ）‎ A． B． C． D．‎ ‎【答案】C 二、填空题 (本大题8个小题，每小题3分，满分24分)‎ ‎11．（2011湖南衡阳，11，3分）计算 ．‎ ‎【答案】‎ ‎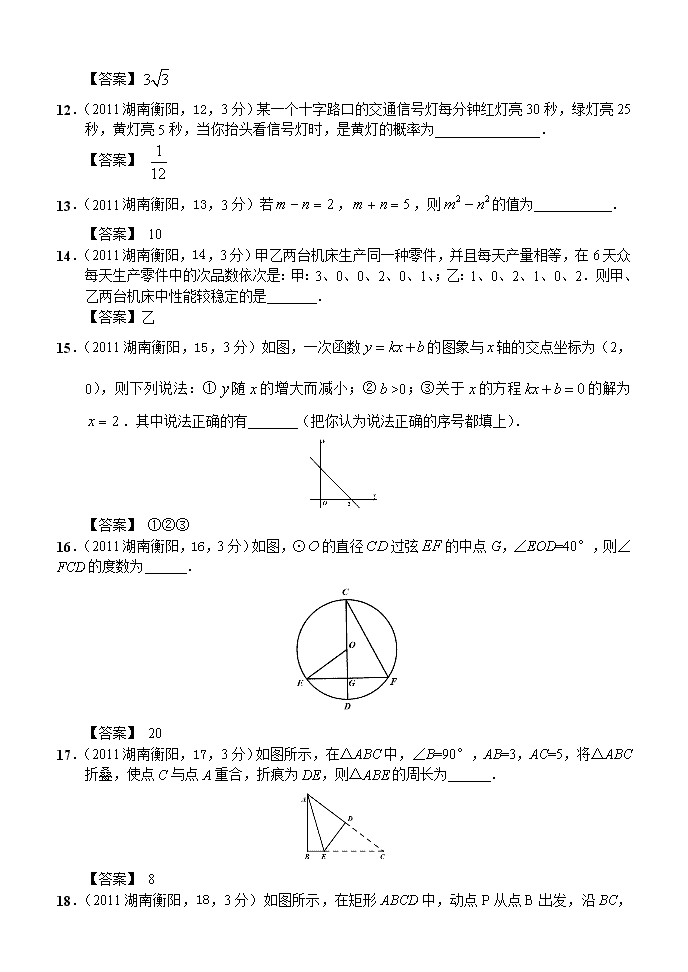12．（2011湖南衡阳，12，3分）某一个十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是黄灯的概率为 ．‎ ‎【答案】 ‎ ‎13．（2011湖南衡阳，13，3分）若，，则的值为 ．‎ ‎【答案】 10‎ ‎14．（2011湖南衡阳，14，3分）甲乙两台机床生产同一种零件，并且每天产量相等，在6天众每天生产零件中的次品数依次是：甲：3、0、0、2、0、1、；乙：1、0、2、1、0、2．则甲、乙两台机床中性能较稳定的是 ．‎ ‎【答案】乙 ‎ ‎15．（2011湖南衡阳，15，3分）如图，一次函数的图象与轴的交点坐标为（2，0），则下列说法：①随的增大而减小；②>0；③关于的方程的解为．其中说法正确的有 （把你认为说法正确的序号都填上）．‎ ‎【答案】 ①②③‎ ‎16．（2011湖南衡阳，16，3分）如图，⊙的直径过弦的中点G，∠EOD=40°，则∠FCD的度数为 ．‎ ‎【答案】 20‎ ‎17．（2011湖南衡阳，17，3分）如图所示，在△ABC中，∠B=90°，AB=3，AC=5，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE的周长为 ．‎ ‎【答案】 8‎ ‎18．（2011湖南衡阳，18，3分）如图所示，在矩形ABCD中，动点P从点B出发，沿BC，‎ CD，DA运动至点A停止，设点P运动的路程为，△ABP的面积为，如果关于的函数图象如图所示，那么△ABC的面积是 ．‎ ‎【答案】 10‎ 三、解答题(本大题共有9个小题，满分66分，解答应写出文字说明、证明过程或演算步骤．)‎ ‎19．（2011湖南衡阳，19，6分）先化简，再求值．，其中．‎ ‎【解】原式==，‎ 当时，原式==+1=．‎ ‎20．（2011湖南衡阳，20，6分）解不等式组，并把解集在数轴上表示出来．‎ ‎【解】 由①得≤3，由②得，不等式组的解集为．解集在数轴上表示为 ‎21．（2011湖南衡阳，21，6分）如图，在△ABC中，AD是中线，分别过点B、C作AD及其延长线的垂线BE、CF，垂足分别为点E、F．求证：BE=CF．‎ ‎【证明】∵在△ABC中，AD是中线，‎ ‎∴BD=CD，∵CF⊥AD，BE⊥AD，∴∠CFD＝∠BED＝90° ，在△BED与△CFD中，∵∠BED＝∠CFD，∠BDE＝∠CDF，BD＝CD，∴△BED≌△CFD，∴BE=CF．‎ ‎22．（2011湖南衡阳，22，6分）李大叔去年承包了10亩地种植甲、乙两种蔬菜，共获利18000元，其中甲种蔬菜每亩获利2000元，乙种蔬菜每亩获利1500元，李大叔去年甲、乙两种蔬菜各种植了多少亩？‎ ‎【解】 设李大叔去年甲种蔬菜种植了亩，乙种蔬菜种植了亩，则 ‎，解得，答李大叔去年甲种蔬菜种植了6亩，乙种蔬菜种植了4亩．‎ ‎23．（2011湖南衡阳，23，6分）我国是世界上严重缺水的国家之一，2011年春季以来，我省遭受了严重的旱情，某校为了组织“节约用水从我做起”活动，随机调查了本校120名同学家庭月人均用水量和节水措施情况，如图10、图11是根据调查结果做出的统计图的一部分．‎ 请根据信息解答下列问题：‎ ‎(1)图10中淘米水浇花所占的百分比为 ；‎ ‎(2)图10中安装节水设备所在的扇形的圆心角度数为 ；‎ ‎(3)补全图11‎ ‎(4)如果全校学生家庭总人数为3000人，根据这120名同学家庭月人均用水量，估计全校学生家庭月用水总量是多少吨？‎ ‎ 图10‎ ‎ 图11‎ ‎【解】 (1)15﹪；(2)108°；‎ ‎(3) 120－10－41－33－16=20，如下图：‎ ‎(4)（30×1＋41×2＋20×3＋33×4＋16×5）÷120=3.2‎ ‎3.2×3000=9600（吨）‎ 答：全校学生家庭月用水总量是9600吨．‎ ‎24．（2011湖南衡阳，24，8分）如图，△ABC内接于⊙O，CA=CB，CD∥AB且与OA的延长线交与点D．‎ ‎(1)判断CD与⊙O的位置关系并说明理由；‎ ‎(2)若∠ACB=120°，OA=2，求CD的长．‎ ‎【解】 (1) CD与⊙O的位置关系是相切，理由如下：‎ 作直径CE，连结AE．‎ ‎∵CE是直径， ∴∠EAC＝90°，∴∠E＋∠ACE=90°，‎ ‎∵CA=CB，∴∠B＝∠CAB，∵AB∥CD，‎ ‎∴∠ACD＝∠CAB，∵∠B＝∠E，∠ACD＝∠E，‎ ‎∴∠ACE＋∠ACD=90°，即∠DCO=90°，‎ ‎∴OC⊥D C，∴CD与⊙O相切．‎ ‎（2）∵CD∥AB，OC⊥D C，∴OC⊥A B，‎ 又∠ACB=120°，∴∠OCA＝∠OCB=60°，‎ ‎∵OA=OC，∴△OAC是等边三角形，‎ ‎∴∠DOA=60°， ‎ ‎∴在Rt△DCO中， =，‎ ‎∴DC=OC=OA=2．‎ ‎25．（2011湖南衡阳，25，8分）如图，已知A，B两点的坐标分别为A(0，)，B(2，0)直线AB与反比例函数的图像交与点C和点D（-1，a）．‎ ‎(1)求直线AB和反比例函数的解析式；‎ ‎(2)求∠ACO的度数；‎ ‎(3)将△OBC绕点O逆时针方向旋转α角（α为锐角），得到△OB′C′，当α为多少度时OC′⊥AB，并求此时线段AB′的长．‎ ‎【解】(1)设直线AB的解析式为，将A(0，)，B(2，0)代入解析式中，得，解得．∴直线AB的解析式为；将D（-1，a）代入得，∴点D坐标为（-1，），将D（-1，）代入中得，∴反比例函数的解析式为．‎ ‎(2)解方程组得，，∴点C坐标为（3，），‎ 过点C作CM⊥轴于点M，则在Rt△OMC中，‎ ‎，，∴，∴，‎ 在Rt△AOB中，=，∴，‎ ‎∴∠ACO=．‎ ‎(3)如图，∵OC′⊥AB，∠ACO=30°，‎ ‎∴= ∠COC′=90°－30°=60°，∠BOB′==60°，‎ ‎∴∠AOB′=90°－∠BOB′=30°，∵ ∠OAB=90°－∠ABO=30°，‎ ‎∴∠AOB′=∠OAB，‎ ‎∴AB′= OB′=2．‎ 答：当α为60度时OC′⊥AB，并求此时线段AB′的长为2．‎ ‎26．（2011湖南衡阳，26，10分）如图，在矩形ABCD中，AD=4，AB=m(m＞4)，点P是AB边上的任意一点（不与A、B重合），连结PD，过点P作PQ⊥PD，交直线BC于点Q．‎ ‎(1)当m=10时，是否存在点P使得点Q与点C重合？若存在，求出此时AP的长；若不存在，说明理由；‎ ‎(2)连结AC，若PQ∥AC,求线段BQ的长（用含m的代数式表示）‎ ‎(3)若△PQD为等腰三角形，求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式，并写出m的取值范围．‎ ‎【解】(1) 假设当m=10时，存在点P使得点Q与点C重合（如下图），‎ ‎∵PQ⊥PD∴∠DPC=90°，∴∠APD＋∠BPC=90°，‎ 又∠ADP＋∠APD=90°，∴∠BPC=∠ADP，‎ 又∠B=∠A=90°，∴△PBC∽△DAP，∴，‎ ‎∴，∴或8，∴存在点P使得点Q与点C重合，出此时AP的长2 或8．‎ ‎(2) 如下图，∵PQ∥AC，∴∠BPQ=∠BAC，∵∠BPQ=∠ADP，∴∠BAC=∠ADP，又∠B=‎ ‎∠DAP=90°，∴△ABC∽△DAP，∴，即，∴．‎ ‎∵PQ∥AC，∴∠BPQ=∠BAC，∵∠B=∠B，∴△PBQ∽△ABC，，即，∴．‎ ‎(3)由已知 PQ⊥PD，所以只有当DP=PQ时，△PQD为等腰三角形（如图），‎ ‎∴∠BPQ=∠ADP，又∠B=∠A=90°，∴△PBQ≌△DAP，‎ ‎∴PB=DA=4，AP=BQ=，‎ ‎∴以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式为：S四边形PQCD= S矩形ABCD－S△DAP－S△QBP=‎ ‎==16（4＜≤8）．‎ ‎27．（2011湖南衡阳，27，10分）已知抛物线．‎ ‎(1)试说明：无论m为何实数，该抛物线与x轴总有两个不同的交点；‎ ‎(2)如图，当该抛物线的对称轴为直线x=3时，抛物线的顶点为点C，直线y=x－1与抛物线交于A、B两点，并与它的对称轴交于点D．‎ ‎①抛物线上是否存在一点P使得四边形ACPD是正方形？若存在，求出点P的坐标；若不存在，说明理由；‎ ‎②平移直线CD，交直线AB于点M，交抛物线于点N，通过怎样的平移能使得C、D、M、N为顶点的四边形是平行四边形．‎ ‎【解】 (1)====，∵不管m为何实数，总有≥0，∴=＞0，∴无论m为何实数，该抛物线与x轴总有两个不同的交点．‎ ‎ (2)∵ 抛物线的对称轴为直线x=3，∴，‎ 抛物线的解析式为=，顶点C坐标为（3，－2），‎ 解方程组，解得或，所以A的坐标为（1，0）、B的坐标为（7，6），∵时y=x－1=3－1=2，∴D的坐标为（3，2），设抛物线的对称轴与轴的交点为E，则E的坐标为（3，0），所以AE=BE=3，DE=CE=2，‎ ① 假设抛物线上存在一点P使得四边形ACPD是正方形，则AP、CD互相垂直平分且相等，于是P与点B重合，但AP=6，CD=4，AP≠CD，故抛物线上不存在一点P使得四边形ACPD是正方形．‎ ② ‎(Ⅰ)设直线CD向右平移个单位（＞0）可使得C、D、M、N为顶点的四边形是平行四边形，则直线CD的解析式为x=3，直线CD与直线y=x－1交于点M（3，2），又∵D的坐标为（3，2），C坐标为（3，－2），∴D通过向下平移4个单位得到C．‎ ‎∵C、D、M、N为顶点的四边形是平行四边形，∴四边形CDMN是平行四边形或四边形CDNM是平行四边形．‎ ‎（ⅰ）当四边形CDMN是平行四边形，∴M向下平移4个单位得N，‎ ‎∴N坐标为（3，），‎ 又N在抛物线上，∴，‎ 解得（不合题意，舍去），，‎ ‎（ⅱ）当四边形CDNM是平行四边形，∴M向上平移4个单位得N，‎ ‎∴N坐标为（3，），‎ 又N在抛物线上，∴，‎ 解得（不合题意，舍去），，‎ ‎(Ⅱ) 设直线CD向左平移个单位（＞0）可使得C、D、M、N为顶点的四边形是平行四边形，则直线CD的解析式为x=3，直线CD与直线y=x－1交于点M（3，2），又∵D的坐标为（3，2），C坐标为（3，－2），∴D通过向下平移4个单位得到C．‎ ‎∵C、D、M、N为顶点的四边形是平行四边形，∴四边形CDMN是平行四边形或四边形CDNM是平行四边形．‎ ‎（ⅰ）当四边形CDMN是平行四边形，∴M向下平移4个单位得N，‎ ‎∴N坐标为（3，），‎ 又N在抛物线上，∴，‎ 解得（不合题意，舍去），（不合题意，舍去），‎ ‎（ⅱ）当四边形CDNM是平行四边形，∴M向上平移4个单位得N，‎ ‎∴N坐标为（3，），‎ 又N在抛物线上，∴，‎ 解得，（不合题意，舍去），‎ 综上所述，直线CD向右平移2或（）个单位或向左平移（）个单位，可使得C、D、M、N为顶点的四边形是平行四边形．‎