2009年浙江省金华市初中毕业生学业考试试卷及答案 9页

‎2009年初中毕业生学业考试(金华卷)‎ 数 学 试 题 卷 考生须知： 1.全卷共三大题,24小题，满分为120分.考试时间为100分钟,本次考试采用开卷形式.‎ ‎2.全卷分为卷Ⅰ（选择题）和卷Ⅱ（非选择题）两部分，全部在答题纸上作答.卷Ⅰ的答案必须用2B铅笔填涂；卷Ⅱ的答案必须用黑色字迹钢笔或签字笔写在答题纸相应位置上.‎ ‎3.请用黑色字迹钢笔或签字笔在答题纸上先填写姓名和准考证号.‎ ‎4.作图时,可先使用2B铅笔,确定后必须使用黑色字迹的钢笔或签字笔描黑.‎ 卷 Ⅰ 说明：本卷共有1大题，10小题，共30分.请用2B铅笔在答题纸上将你认为正确的选项对应的小方框涂黑、涂满.‎ 一、选择题(本题有10小题,每小题3分,共30分)‎ ‎1.下列四个数中，比-2小的数是（ ▲ ）‎ A.2 　 B.‎-3 　 ‎ C．0 　　　D.-1.5‎ ‎2.抛物线的对称轴是（ ▲ ）‎ Ａ.直线x= -2　 B.直线 x=‎2 C.直线x= -3 D.直线x=3‎ ‎3.要把分式方程化为整式方程，方程两边可同时乘以（ ▲ ）‎ 俯视图 ‎ 主视图 A. B. C. D.‎ ‎4.一个几何体及它的主视图和俯视图如图所示，那么它的左视图 正确的是（ ▲ ）‎ A B C D ‎5.下列运用平方差公式计算，错误的是（ ▲ )‎ A. B. ‎ C. D. ‎ ‎1‎ ‎0‎ ‎3‎ ‎-2‎ ‎2‎ ‎-1‎ C D ‎1‎ ‎0‎ ‎3‎ ‎-2‎ ‎2‎ ‎-1‎ ‎0‎ B ‎1‎ ‎3‎ ‎-2‎ ‎2‎ ‎-1‎ A ‎6.不等式组的解在数轴上表示正确的是（ ▲ ) ‎ ‎1‎ ‎0‎ ‎3‎ ‎-2‎ ‎2‎ ‎-1‎ ‎ ‎ ‎2‎ ‎1‎ ‎7.如图，把一块直角三角板的直角顶点放在直尺的一边上，‎ 如果∠1=32o，那么∠2的度数是（ ▲ ）‎ A.32o B.58o C.68o D.60o ‎ ‎8.在北京奥运会上，我国健儿奋力拼搏，共获得了100枚奖牌，其中游泳 ‎6枚，射击8枚，球类21枚，举重9枚，体操13枚等.数据6,8,21,9,13的中位数是（ ▲ ）‎ A.8　 B‎.21 ‎C．9 　 D.13‎ ‎9.从2，-2，1，-1四个数中任取2个数求和，其和为0的概率是（ ▲ )‎ A. B． C． D．‎ t t t s s s O O O A B ‎ ‎ ‎ ‎ ‎ ‎ C D t s O ‎10.小明在一直道上骑自行车，经过起步、加速、匀速、减速之后停车.设小明骑车的时间为t（秒）,骑车的路程为s（米）,则s关于t的函数图像大致是（ ▲ )‎ 卷 Ⅱ 说明：本卷共有2大题，14小题，共90分.请用黑色字迹钢笔或签字笔将答案写在答题纸的相应位置上.‎ O B C D A 二、填空题 (本题有6小题,每小题4分,共24分)‎ ‎11.因式分解: x2+x= ▲ .‎ ‎12.一商场开展“家电下乡”活动，某品牌彩电三天的销量分别是 ‎6，10，14（单位：台），该品牌彩电这三天的日平均销量是 ▲ 台.‎ ‎13.如图,⊙O是正△ABC的外接圆，点D是弧AC上一点，则∠BDC 的度数是 ▲ .‎ α ‎14.在直角坐标系中，已知点A(3,2).作点A关于y轴的对称点为A1, ‎ 作点A1关于原点的对称点为A2, 作点A2关于x轴的对称点为A３，‎ 作点A３关于y轴的对称点为A4，…按此规律，则点A8的坐标 为 ▲ .　　　　　　　　　　　　　　　　　‎ ‎15.“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一 个大正方形．如果小正方形的面积为4，大正方形的面积为100，直 O x A y H C y=x2‎ 角三角形中较小的锐角为α，则tanα的值等于 ▲ .‎ ‎16.如图，在第一象限内作射线OC,与x轴的夹角为30o,在射线 OC上取点A，过点A作AH⊥x轴于点H.在抛物线y=x2 (x>0)‎ 上取点P，在y轴上取点Q，使得以P，O，Q为顶点的三角形与 ‎△AOH全等，则符合条件的点A的坐标是 ▲ .‎ 三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程)‎ ‎17.(本题6分) ‎ 计算:. 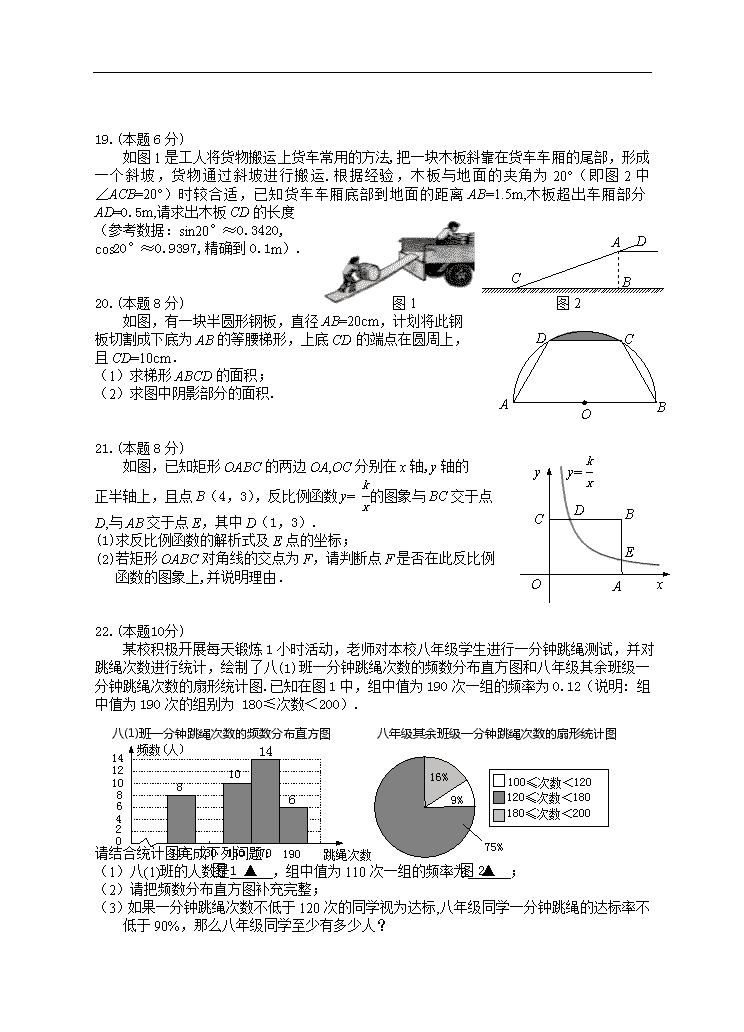‎ ‎18.(本题6分)‎ E A B D C F 如图，已知点B，F，C，E在同一直线上，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AB＝DE.请添加一个条件，使AC=DF(不再添加其它线段，不再标注或使用其他字母),并给出证明.‎ ‎ 添加的条件是: ▲ ． ‎ 证明:‎ ‎19.(本题6分)‎ A B C D 图1 图2‎ 如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部，形成一个斜坡，货物通过斜坡进行搬运.根据经验，木板与地面的夹角为20°（即图2中∠ACB=20°）时较合适，已知货车车厢底部到地面的距离AB=‎1.5m,木板超出车厢部分AD=‎0.5m,请求出木板CD的长度 ‎（参考数据：sin20°≈0.3420,‎ cos20°≈0.9397,精确到‎0.1m）.‎ ‎20.(本题8分)‎ O B A C D 如图，有一块半圆形钢板，直径AB=‎20cm，计划将此钢 板切割成下底为AB的等腰梯形，上底CD的端点在圆周上，‎ 且CD=‎10cm．‎ ‎（1）求梯形ABCD的面积；‎ ‎（2）求图中阴影部分的面积.‎ x y O C A B E D y= ‎21.(本题8分)‎ 如图，已知矩形OABC的两边OA,OC分别在x轴,y轴的 正半轴上，且点B（4，3），反比例函数y= 的图象与BC交于点 D,与AB交于点E，其中D（1，3）.‎ ‎(1)求反比例函数的解析式及E点的坐标；‎ ‎(2)若矩形OABC对角线的交点为F，请判断点F是否在此反比例 ‎ 函数的图象上,并说明理由．‎ ‎22.(本题10分)‎ ‎ 某校积极开展每天锻炼1小时活动，老师对本校八年级学生进行一分钟跳绳测试，并对跳绳次数进行统计，绘制了八(1)班一分钟跳绳次数的频数分布直方图和八年级其余班级一分钟跳绳次数的扇形统计图.已知在图1中，组中值为190次一组的频率为0.12（说明: 组中值为190次的组别为 180≤次数＜200）.‎ 八年级其余班级一分钟跳绳次数的扇形统计图 ‎100≤次数＜120‎ ‎120≤次数＜180‎ ‎180≤次数＜200‎ ‎9%‎ ‎16%‎ ‎75%‎ ‎14‎ ‎12‎ ‎10‎ 八(1)班一分钟跳绳次数的频数分布直方图 跳绳次数 频数(人) ‎ ‎8‎ ‎10‎ ‎14‎ ‎6‎ ‎8‎ ‎6‎ ‎4‎ ‎2‎ ‎0‎ ‎110 ‎ ‎130 ‎ ‎190 ‎ ‎170 ‎ ‎150 ‎ 图1 图2‎ ‎ ‎ 请结合统计图完成下列问题：‎ ‎（1）八(1)班的人数是 ▲ ，组中值为110次一组的频率为 ▲ ；‎ ‎（2）请把频数分布直方图补充完整；‎ ‎（3）如果一分钟跳绳次数不低于120次的同学视为达标,八年级同学一分钟跳绳的达标率不低于90%，那么八年级同学至少有多少人？‎ ‎23.(本题10分)‎ 在平面直角坐标系中，O为坐标原点.‎ ‎(1)已知点A(3,1)，连结OA，平移线段OA，使点O落在点B.设点A落在点C,作如下探究：‎ 探究一：若点B的坐标为(1，2)，请在图1中作出平移后的像，则点C的坐标是 ▲ ；连结AC，BO，请判断O，A，C，B四点构成的图形的形状，并说明理由；‎ y B A O x 图1‎ ‎1‎ x O A B y 图2‎ ‎1‎ 探究二：若点B的坐标为(6，2)，按探究一的方法,判断O，A，B,C四点构成的图形的形状（直接写出结论即可）.‎ ‎（温馨提示:作图时,别忘了用黑色字迹的钢笔或签字笔描黑喔!）‎ ‎(2)通过上面的探究，请直接回答下列问题：‎ ‎①若已知三点A (a，b)，B(c，d)，C (a+c，b+d)，顺次连结O，A，C，B，请判断所得到的图形的形状；‎ ‎②在①的条件下，如果所得到的图形是菱形或者是正方形，请选择一种情况，写出a，b，c，d应满足的关系式.‎ ‎24.(本题12分)‎ 如图，在平面直角坐标系中，点A（0，6），点B是x轴上的一个动点，连结AB，取AB的中点M，将线段MB绕点B按顺时针方向旋转90o，得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是（t，0）.‎ ‎（1）当t=4时，求直线AB的解析式；‎ ‎（2）当t>0时，用含t的代数式表示点C的坐标及△ABC的面积；‎ ‎（3）是否存在点B,使△ABD为等腰三角形?若存在，请求出所有符合条件的点B的坐标；若不存在，请说明理由.‎ ‎·‎ y O A x 备用图 M y O C A B x D ‎2009年初中毕业生学业水平考试(金华卷)数学试卷参考答案及评分标准 一、 选择题（本题共10小题，每小题3分，共30分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B B D B C A B C C D 评分标准 选对一题给3分，不选，多选，错选均不给分 二、填空题（本题有6小题，每小题4分，共24分）‎ ‎11．x(x+1)； 12.10； 13.60°； 14.（3，-2）；‎ ‎15.； 16. (3，) , (，) , (2，2) , (，).（每个1分）‎ 三、解答题（本题有8小题，共66分）‎ ‎17.(本题6分) ‎ ‎=2009－1－1…………………………………5分（写对一个2分，两个4分，三个5分）‎ ‎=2007…………………………………………1分 ‎18. (本题6分)‎ 添加的条件例举：BC=EF，∠A=∠D，∠ACB=∠DFE，BF=CE等.……2分（写出一个即可）‎ 证明例举（以添加条件BC=EF为例）：‎ ‎∵ AB⊥BE，DE⊥BE，‎ ‎∴∠ABC=∠DEF=90°.………………………………………………………………1分 ‎∵BC＝EF，AB＝DE，‎ ‎∴△ABC≌△DEF（SAS）. ………………………………………………………2分 ‎ ∴AC=DF．……………………………………………………………………………1分 ‎19. (本题6分)‎ 由题意可知：AB⊥BC ‎∴在Rt△ABC中, sin∠ACB=　……………………………………………2分 ‎∴AC= = ≈4.39（m）………………………………３分 ‎∴CD = AC+AD≈ 4.39+0.5 = 4.89 ≈ 4.9（m）‎ 答：木板的长度约为‎4.9m.……………………………………………１分 O E B A C D ‎20.(本题8分)‎ ‎(1)连结OC，OD，过点O作OE⊥CD于点E.………………1分 ‎∵OE⊥CD，∴CE=DE=5, ……………………………………1分 ‎∴OE==5, ………………2分 ‎∴S梯形ABCD= (AB+CD) OE =75(cm2).……………………1分 ‎(2) ∵S扇形= ×100·π= π (cm2) ，…………………………………………………………1分 ‎ S△OCD=·OE·CD= 25 (cm2)， ………………………………………………………1分 ‎∴S阴影= S扇形－S△OCD= (π－25) cm2，‎ ‎∴阴影部分的面积为(π－25) cm2. ……………………………………1分 ‎21.(本题8分)‎ ‎（１）把D (1，3)代入y= 得3= 　∴k=3‎ ‎∴ y= …………………………………………………2分 当x=4时，y= ∴E（４，）……………………………２分 ‎（２）点F在反比例函数的图象上．…………………１分 理由如下：‎ A B C D E F H O x y y= 连结AC,OB交于点F，过F作FH⊥x轴于H.‎ ‎∵四边形OABC是矩形 ‎∴OF=FB= OB 又∵∠FHO=∠BAO=Rt∠, ∠FOH=∠BOA ‎∴△OFH∽△OBA ‎∴= = = ‎∴OH=2, FH= ‎ ‎∴F（２，）……………………………………………………２分 当x=2时，y= = ‎∴点F在反比例函数 y= 的图象上．…………………………１分 ‎22.(本题10分)‎ ‎（1）50，0.16 ………………………………………………4分 ‎（2）组中值为130次一组的频数为12人，图略………………………………………2分 ‎（3）设八年级同学有x人，‎ 则可得不等式：‎ ‎ 42+0.91(x－50)≥0.9x …………………………………………3分 解得x≥350‎ 答：八年级同学至少有350人. …………………………1分 ‎23.(本题10分)‎ ‎(1)探究一： C (4，3)，……………………………………………………1分 图正确得2分，图略…………………………………………2分 四边形OACB为平行四边形，………………………………1分 理由如下：‎ 由平移可知，OA∥BC且OA=BC，‎ 所以四边形OACB为平行四边形.…………………………2分 探究二：线段…………………………………………………………1分 ‎(2) ①平行四边形或线段………………………………………2分 ‎②菱形：a2+b2=c2+d2 （a=－c，b=－d除外）‎ 正方形：或……………………………1分 ‎(写出菱形需满足的条件或写出正方形需满足的条件其中一种即可给分)‎ ‎24.(本题12分)‎ 解：（1）当t=4时，B(4,0)‎ 设直线AB的解析式为y= kx+b .‎ 把 A(0,6)，B(4,0) 代入得：‎ ‎ , 解得： ,‎ ‎∴直线AB的解析式为：y=－x+6.………………………………………4分 ‎(2) 过点C作CE⊥x轴于点E 由∠AOB=∠CEB=90°，∠ABO=∠BCE，得△AOB∽△BEC.‎ ‎∴，‎ ‎∴BE= AO=3，CE= OB= ，‎ ‎∴点C的坐标为(t+3，).…………………………………………………………2分 方法一：‎ y O C A B x D E S梯形AOEC= OE·(AO+EC)= (t+3)(6+)=t2+t+9，‎ S△ AOB= AO·OB= ×6·t=3t，‎ S△ BEC= BE·CE= ×3×= t，‎ ‎∴S△ ABC= S梯形AOEC－ S△ AOB－S△ BEC ‎ = t2+t+9－3t－t = t2+9.‎ 方法二：‎ ‎∵AB⊥BC，AB=2BC，∴S△ ABC= AB·BC= BC2.‎ 在Rt△BCE中，BC2= CE2+ BE2 = t2+9，‎ 即S△ ABC= t2+9.…………………………………………………………2分 y O C A B x D E ‎(3)存在，理由如下：‎ ‎①当t≥0时. ‎ Ⅰ.若AD＝BD.‎ 又∵BD∥y轴 ‎∴∠OAB=∠ABD，∠BAD=∠ABD，‎ ‎∴∠OAB=∠BAD.‎ 又∵∠AOB=∠ABC，‎ ‎∴△ABO∽△ACB，‎ ‎∴，‎ ‎∴= ，‎ ‎∴t=3，即B(3，0).‎ Ⅱ.若AB＝AD.‎ 延长AB与CE交于点G，‎ 又∵BD∥CG ‎∴AG＝AC y O C A B D E H G x 过点A画AH⊥CG于H．‎ ‎∴CH＝HG＝CG 由△AOB∽△GEB，‎ 得＝ ，‎ ‎∴GE= .‎ 又∵HE＝AO＝６，CE＝ ‎∴＋６＝×（＋）‎ y O C A B x D E F ‎∴t2-24t-36=0‎ 解得：t=12±6. 因为 t≥0，‎ 所以t=12＋6，即B(12＋6，0).‎ Ⅲ.由已知条件可知，当0≤t<12时，∠ADB为钝角，故BD ≠ AB.‎ ‎ 当t≥12时，BD≤CE