中考模拟试卷 23页

中考模拟试卷 一．选择题（共10小题）‎ ‎1．“五一”期间，某市共接待海内外游客约567000人次，将567000用科学记数法表示为（　　）‎ A．567×103 B．56.7×104 C．5.67×105 D．0.567×106‎ ‎2．已知点A（a，1）与点B（﹣4，b）关于原点对称，则a+b的值为（　　）‎ A．5 B．﹣5 C．3 D．﹣3‎ ‎3．下列运算正确的是（　　）‎ A．﹣3（x﹣4）=﹣3x+12 B．（﹣3x）2•4x2=﹣12x4‎ C．3x+2x2=5x3 D．x6÷x2=x3‎ ‎4．下列命题是真命题的是（　　）‎ A．四边都相等的四边形是矩形 B．菱形的对角线相等 C．对角线互相垂直的平行四边形是正方形 D．对角线相等的平行四边形是矩形 ‎5．一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1，2，3，4，随机摸出一个小球后不放回，再随机摸出一个小球，则两次摸出的小球标号之和等于5的概率为（　　）‎ A． B． C． D．‎ ‎6．由于受H7N9禽流感的影响，我市某城区今年2月份鸡的价格比1月份下降a%，3月份比2月份下降b%，已知1月份鸡的价格为24元/千克．设3月份鸡的价格为m元/千克，则（　　）‎ A．m=24（1﹣a%﹣b%） B．m=24（1﹣a%）b% C．m=24﹣a%﹣b% D．m=24（1﹣a%）（1﹣b%）‎ ‎7．如图，在矩形ABCD中，点E是边BC的中点，AE⊥BD，垂足为F，则tan∠BDE的值是（　　）‎ 第23页（共23页）‎ A． B． C． D．‎ ‎8．如图，一艘海轮位于灯塔P的南偏东45°方向，距离灯塔60n mile的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东30°方向上的B处，这时，B处与灯塔P的距离为（　　）‎ A．60 n mile B．60 n mile C．30 n mile D．30 n mile ‎9．已知抛物线y=x2+1具有如下性质：该抛物线上任意一点到定点F（0，2）的距离与到x轴的距离始终相等，如图，点M的坐标为（，3），P是抛物线y=x2+1上一个动点，则△PMF周长的最小值是（　　）‎ A．3 B．4 C．5 D．6‎ ‎10．下列二次根式中，最简二次根式是（　　）‎ A． B． C． D．‎ ‎　‎ 二．填空题（共6小题）‎ ‎11．计算（﹣）﹣1=　 　．‎ ‎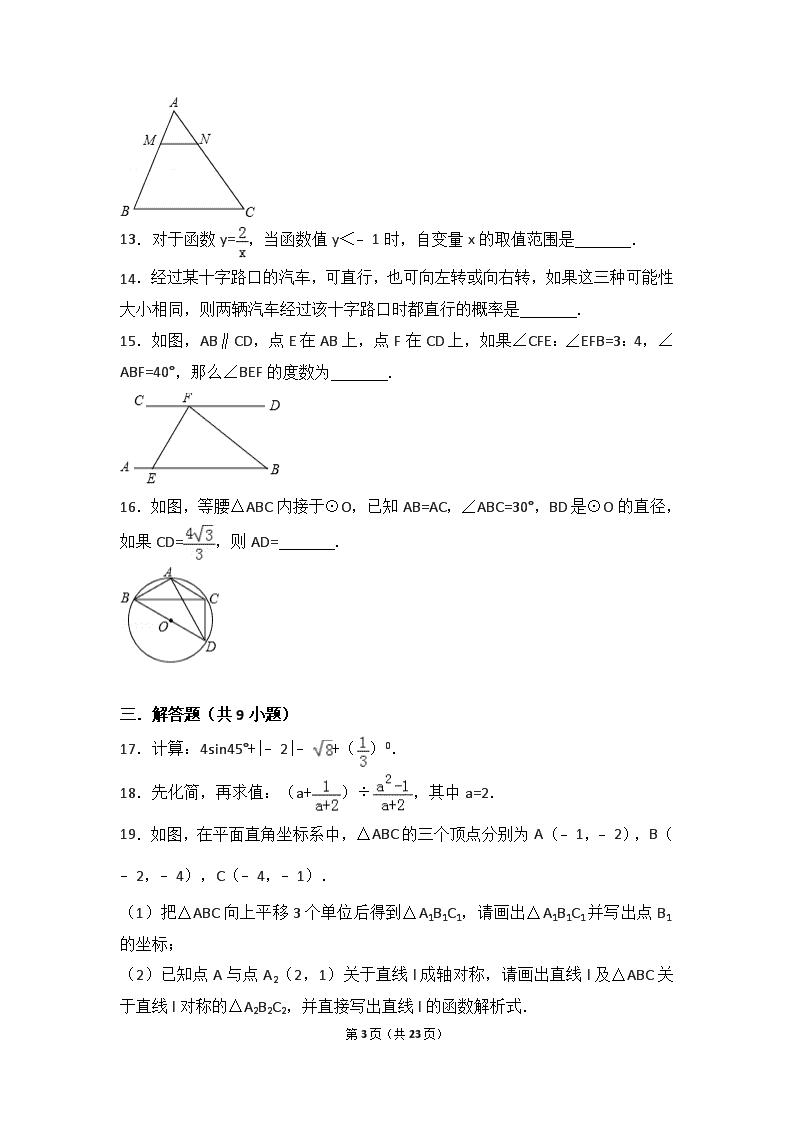12．在△ABC中，MN∥BC 分别交AB，AC于点M，N；若AM=1，MB=2，BC=3，则MN的长为　 　．‎ 第23页（共23页）‎ ‎13．对于函数y=，当函数值y＜﹣1时，自变量x的取值范围是　 　．‎ ‎14．经过某十字路口的汽车，可直行，也可向左转或向右转，如果这三种可能性大小相同，则两辆汽车经过该十字路口时都直行的概率是　 　．‎ ‎15．如图，AB∥CD，点E在AB上，点F在CD上，如果∠CFE：∠EFB=3：4，∠ABF=40°，那么∠BEF的度数为　 　．‎ ‎16．如图，等腰△ABC内接于⊙O，已知AB=AC，∠ABC=30°，BD是⊙O的直径，如果CD=，则AD=　 　．‎ ‎　‎ 三．解答题（共9小题）‎ ‎17．计算：4sin45°+|﹣2|﹣+（）0．‎ ‎18．先化简，再求值：（a+）÷，其中a=2．‎ ‎19．如图，在平面直角坐标系中，△ABC的三个顶点分别为A（﹣1，﹣2），B（﹣2，﹣4），C（﹣4，﹣1）．‎ ‎（1）把△ABC向上平移3个单位后得到△A1B1C1，请画出△A1B1C1并写出点B1的坐标；‎ ‎（2）已知点A与点A2（2，1）关于直线l成轴对称，请画出直线l及△ABC关于直线l对称的△A2B2C2，并直接写出直线l的函数解析式．‎ 第23页（共23页）‎ ‎20．随着经济的快速发展，环境问题越来越受到人们的关注，某校学生会为了解节能减排、垃圾分类知识的普及情况，随机调查了部分学生，调查结果分为“非常了解”“了解”“了解较少”“不了解”四类，并将调查结果绘制成下面两个统计图．‎ ‎（1）本次调查的学生共有　 　人，估计该校1200名学生中“不了解”的人数是　 　人；‎ ‎（2）“非常了解”的4人有A1，A2两名男生，B1，B2两名女生，若从中随机抽取两人向全校做环保交流，请利用画树状图或列表的方法，求恰好抽到一男一女的概率．‎ ‎21．如图，点E，F分别在菱形ABCD的边DC，DA上，且CE=AF．‎ 求证：∠ABF=∠CBE．‎ ‎22．如图，在平面直角坐标系xOy中，已知正比例函数y=x的图象与反比例函数y=的图象交于A（a，﹣2），B两点．‎ ‎（1）求反比例函数的表达式和点B的坐标；‎ 第23页（共23页）‎ ‎（2）P是第一象限内反比例函数图象上一点，过点P作y轴的平行线，交直线AB于点C，连接PO，若△POC的面积为3，求点P的坐标．‎ ‎23．随着地铁和共享单车的发展，“地铁+单车”已成为很多市民出行的选择，李华从文化宫站出发，先乘坐地铁，准备在离家较近的A，B，C，D，E中的某一站出地铁，再骑共享单车回家，设他出地铁的站点与文化宫距离为x（单位：千米），乘坐地铁的时间y1（单位：分钟）是关于x的一次函数，其关系如下表：‎ ‎ 地铁站 ‎ A ‎ B ‎ C ‎ D ‎ E ‎ x（千米）‎ ‎ 8‎ ‎ 9‎ ‎ 10‎ ‎ 11.5‎ ‎ 13‎ ‎ y1（分钟）‎ ‎ 18‎ ‎ 20‎ ‎ 22‎ ‎ 25‎ ‎ 28‎ ‎（1）求y1关于x的函数表达式；‎ ‎（2）李华骑单车的时间（单位：分钟）也受x的影响，其关系可以用y2=x2﹣11x+78来描述，请问：李华应选择在那一站出地铁，才能使他从文化宫回到家所需的时间最短？并求出最短时间．‎ ‎24．如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．‎ ‎（1）求证：△ECF∽△GCE；‎ ‎（2）求证：EG是⊙O的切线；‎ ‎（3）延长AB交GE的延长线于点M，若tanG=，AH=3，求EM的值．‎ 第23页（共23页）‎ ‎25．如图1，在平面直角坐标系xOy中，抛物线C：y=ax2+bx+c与x轴相交于A，B两点，顶点为D（0，4），AB=4，设点F（m，0）是x轴的正半轴上一点，将抛物线C绕点F旋转180°，得到新的抛物线C′．‎ ‎（1）求抛物线C的函数表达式；‎ ‎（2）若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围．‎ ‎（3）如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P在抛物线C′上的对应点P′，设M是C上的动点，N是C′上的动点，试探究四边形PMP′N能否成为正方形？若能，求出m的值；若不能，请说明理由．‎ ‎　‎ 第23页（共23页）‎ 参考答案与试题解析 ‎　‎ 一．选择题（共10小题）‎ ‎1．“五一”期间，某市共接待海内外游客约567000人次，将567000用科学记数法表示为（　　）‎ A．567×103 B．56.7×104 C．5.67×105 D．0.567×106‎ ‎【解答】解：567000=5.67×105，‎ 故选：C．‎ ‎2．已知点A（a，1）与点B（﹣4，b）关于原点对称，则a+b的值为（　　）‎ A．5 B．﹣5 C．3 D．﹣3‎ ‎【【解答】解：由A（a，1）关于原点的对称点为B（﹣4，b），得 a=4，b=﹣1，‎ a+b=3，‎ 故选：C．‎ ‎3．下列运算正确的是（　　）‎ A．﹣3（x﹣4）=﹣3x+12 B．（﹣3x）2•4x2=﹣12x4‎ C．3x+2x2=5x3 D．x6÷x2=x3‎ ‎【解答】解：∵﹣3（x﹣4）=﹣3x+12，故选项A正确，‎ ‎∵（﹣3x）2•4x2=9x2•4x2=36x4，故选项B错误，‎ ‎∵3x+2x2不能合并，故选项C错误，‎ ‎∵x6÷x2=x4，故选项D错误，‎ 故选A．‎ ‎4．下列命题是真命题的是（　　）‎ A．四边都相等的四边形是矩形 B．菱形的对角线相等 第23页（共23页）‎ C．对角线互相垂直的平行四边形是正方形 D．对角线相等的平行四边形是矩形 ‎【解答】解：A、四边都相等的四边形是菱形，故错误；‎ B、矩形的对角线相等，故错误；‎ C、对角线互相垂直的平行四边形是菱形，故错误；‎ D、对角线相等的平行四边形是矩形，正确，‎ 故选D．‎ ‎5．一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1，2，3，4，随机摸出一个小球后不放回，再随机摸出一个小球，则两次摸出的小球标号之和等于5的概率为（　　）‎ A． B． C． D．‎ ‎【解答】解：画树状图得：‎ ‎∵共有12种等可能的结果，两次摸出的小球标号之和等于5的有4种情况，‎ ‎∴两次摸出的小球标号之和等于5的概率是：=．‎ 故选：C．‎ ‎6．由于受H7N9禽流感的影响，我市某城区今年2月份鸡的价格比1月份下降a%，3月份比2月份下降b%，已知1月份鸡的价格为24元/千克．设3月份鸡的价格为m元/千克，则（　　）‎ A．m=24（1﹣a%﹣b%） B．m=24（1﹣a%）b% C．m=24﹣a%﹣b% D．m=24（1﹣a%）（1﹣b%）‎ ‎【解答】解：∵今年2月份鸡的价格比1月份下降a%，1月份鸡的价格为24元/千克，‎ ‎∴2月份鸡的价格为24（1﹣a%），‎ ‎∵3月份比2月份下降b%，‎ 第23页（共23页）‎ ‎∴三月份鸡的价格为24（1﹣a%）（1﹣b%），‎ 故选D．‎ ‎　‎ ‎7．如图，在矩形ABCD中，点E是边BC的中点，AE⊥BD，垂足为F，则tan∠BDE的值是（　　）‎ A． B． C． D．‎ ‎【解答】解：∵四边形ABCD是矩形，‎ ‎∴AD=BC，AD∥BC，‎ ‎∵点E是边BC的中点，‎ ‎∴BE=BC=AD，‎ ‎∴△BEF∽△DAF，‎ ‎∴=，‎ ‎∴EF=AF，‎ ‎∴EF=AE，‎ ‎∵点E是边BC的中点，‎ ‎∴由矩形的对称性得：AE=DE，‎ ‎∴EF=DE，设EF=x，则DE=3x，‎ ‎∴DF==2x，‎ ‎∴tan∠BDE===；‎ 故选：A．‎ ‎8．如图，一艘海轮位于灯塔P的南偏东45°方向，距离灯塔60n mile的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东30°方向上的B处，这时，B处与灯塔P的距离为（　　）‎ 第23页（共23页）‎ A．60 n mile B．60 n mile C．30 n mile D．30 n mile ‎【解答】解：如图作PE⊥AB于E．‎ 在Rt△PAE中，∵∠PAE=45°，PA=60n mile，‎ ‎∴PE=AE=×60=30n mile，‎ 在Rt△PBE中，∵∠B=30°，‎ ‎∴PB=2PE=60n mile，‎ 故选B ‎9．已知抛物线y=x2+1具有如下性质：该抛物线上任意一点到定点F（0，2）的距离与到x轴的距离始终相等，如图，点M的坐标为（，3），P是抛物线y=x2+1上一个动点，则△PMF周长的最小值是（　　）‎ A．3 B．4 C．5 D．6‎ ‎【解答】解：过点M作ME⊥x轴于点E，交抛物线y=x2+1于点P，此时△PMF周长最小值，‎ ‎∵F（0，2）、M（，3），‎ ‎∴ME=3，FM==2，‎ ‎∴△PMF周长的最小值=ME+FM=3+2=5．‎ 第23页（共23页）‎ 故选C．‎ ‎10．下列二次根式中，最简二次根式是（　　）‎ A． B． C． D．‎ ‎【解答】解：A、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故A符合题意；‎ B、被开方数含能开得尽方的因数或因式，故B不符合题意；‎ C、被开方数含分母，故C不符合题意；‎ D、被开方数含能开得尽方的因数或因式，故D不符合题意；‎ 故选：A．‎ 二．填空题（共6小题）‎ ‎11．计算（﹣）﹣1=　﹣2　．‎ ‎【解答】解：原式==﹣2，‎ 故答案为﹣2．‎ ‎12．在△ABC中，MN∥BC 分别交AB，AC于点M，N；若AM=1，MB=2，BC=3，则MN的长为　1　．‎ ‎【解答】解：∵MN∥BC，‎ ‎∴△AMN∽△ABC，‎ ‎∴，即，‎ ‎∴MN=1，‎ 第23页（共23页）‎ 故答案为：1．‎ ‎13．对于函数y=，当函数值y＜﹣1时，自变量x的取值范围是　﹣2＜x＜0　．‎ ‎【解答】解：∵当y=﹣1时，x=﹣2，‎ ‎∴当函数值y＜﹣1时，﹣2＜x＜0．‎ 故答案为：﹣2＜x＜0．‎ ‎14．经过某十字路口的汽车，可直行，也可向左转或向右转，如果这三种可能性大小相同，则两辆汽车经过该十字路口时都直行的概率是　　．‎ ‎【解答】解：画树状图为：‎ 共有9种等可能的结果数，其中两辆汽车都直行的结果数为1，‎ 所以则两辆汽车都直行的概率为，‎ 故答案为：．‎ ‎15．如图，AB∥CD，点E在AB上，点F在CD上，如果∠CFE：∠EFB=3：4，∠ABF=40°，那么∠BEF的度数为　60°　．‎ ‎【解答】解：∵AB∥CD，∠ABF=40°，‎ ‎∴∠CFB=180°﹣∠B=140°，‎ 又∵∠CFE：∠EFB=3：4，‎ ‎∴∠CFE=∠CFB=60°，‎ ‎∵AB∥CD，‎ ‎∴∠BEF=∠CFE=60°，‎ 故答案为：60°．‎ 第23页（共23页）‎ ‎16．如图，等腰△ABC内接于⊙O，已知AB=AC，∠ABC=30°，BD是⊙O的直径，如果CD=，则AD=　4　．‎ ‎【解答】解：∵AB=AC，‎ ‎∴∠ABC=∠ACB=∠ADB=30°，‎ ‎∵BD是直径，‎ ‎∴∠BAD=90°，∠ABD=60°，‎ ‎∴∠CBD=∠ABD﹣∠ABC=30°，‎ ‎∴∠ABC=∠CBD，‎ ‎∴==，‎ ‎∴=，‎ ‎∴AD=CB，‎ ‎∵∠BCD=90°，‎ ‎∴BC=CD•tan60°=•=4，‎ ‎∴AD=BC=4．‎ 故答案为4．‎ 三．解答题（共9小题）‎ ‎17．计算：4sin45°+|﹣2|﹣+（）0．‎ ‎【解答】解：4sin45°+|﹣2|﹣+（）0‎ ‎=4×+2﹣2+1‎ ‎=2﹣2+3‎ 第23页（共23页）‎ ‎=3．‎ ‎18．先化简，再求值：（a+）÷，其中a=2．‎ ‎【解答】解：（a+）÷，‎ ‎=[+]‎ ‎=‎ ‎=‎ 当a=2时，原式==3．‎ ‎19．如图，在平面直角坐标系中，△ABC的三个顶点分别为A（﹣1，﹣2），B（﹣2，﹣4），C（﹣4，﹣1）．‎ ‎（1）把△ABC向上平移3个单位后得到△A1B1C1，请画出△A1B1C1并写出点B1的坐标；‎ ‎（2）已知点A与点A2（2，1）关于直线l成轴对称，请画出直线l及△ABC关于直线l对称的△A2B2C2，并直接写出直线l的函数解析式．‎ ‎【解答】解：（1）如图，△A1B1C1即为所求，B1（﹣2，﹣1）；‎ ‎（2）如图，△A2B2C2即为所求，直线l的函数解析式为y=﹣x．‎ 第23页（共23页）‎ ‎20．随着经济的快速发展，环境问题越来越受到人们的关注，某校学生会为了解节能减排、垃圾分类知识的普及情况，随机调查了部分学生，调查结果分为“非常了解”“了解”“了解较少”“不了解”四类，并将调查结果绘制成下面两个统计图．‎ ‎（1）本次调查的学生共有　50　人，估计该校1200名学生中“不了解”的人数是　360　人；‎ ‎（2）“非常了解”的4人有A1，A2两名男生，B1，B2两名女生，若从中随机抽取两人向全校做环保交流，请利用画树状图或列表的方法，求恰好抽到一男一女的概率．‎ ‎【解答】解：（1）4÷8%=50（人），‎ ‎1200×（1﹣40%﹣22%﹣8%）=360（人）；‎ 故答案为：50，360；‎ ‎（2）画树状图，共有12根可能的结果，恰好抽到一男一女的结果有8个，‎ ‎∴P（恰好抽到一男一女的）==．‎ ‎21．如图，点E，F分别在菱形ABCD的边DC，DA上，且CE=AF．‎ 第23页（共23页）‎ 求证：∠ABF=∠CBE．‎ ‎【解答】证明：∵四边形ABCD是菱形，‎ ‎∴AB=BC，∠A=∠C，‎ ‎∵在△ABF和△CBE中，，‎ ‎∴△ABF≌△CBE（SAS），‎ ‎∴∠ABF=∠CBE．‎ ‎22．如图，在平面直角坐标系xOy中，已知正比例函数y=x的图象与反比例函数y=的图象交于A（a，﹣2），B两点．‎ ‎（1）求反比例函数的表达式和点B的坐标；‎ ‎（2）P是第一象限内反比例函数图象上一点，过点P作y轴的平行线，交直线AB于点C，连接PO，若△POC的面积为3，求点P的坐标．‎ ‎【解答】解：（1）把A（a，﹣2）代入y=x，可得a=﹣4，‎ ‎∴A（﹣4，﹣2），‎ 把A（﹣4，﹣2）代入y=，可得k=8，‎ ‎∴反比例函数的表达式为y=，‎ ‎∵点B与点A关于原点对称，‎ 第23页（共23页）‎ ‎∴B（4，2）；‎ ‎（2）如图所示，过P作PE⊥x轴于E，交AB于C，‎ 设P（m，），则C（m，m），‎ ‎∵△POC的面积为3，‎ ‎∴m×|m﹣|=3，‎ 解得m=2或2，‎ ‎∴P（2，）或（2，4）．‎ ‎23．随着地铁和共享单车的发展，“地铁+单车”已成为很多市民出行的选择，李华从文化宫站出发，先乘坐地铁，准备在离家较近的A，B，C，D，E中的某一站出地铁，再骑共享单车回家，设他出地铁的站点与文化宫距离为x（单位：千米），乘坐地铁的时间y1（单位：分钟）是关于x的一次函数，其关系如下表：‎ ‎ 地铁站 ‎ A ‎ B ‎ C ‎ D ‎ E ‎ x（千米）‎ ‎ 8‎ ‎ 9‎ ‎ 10‎ ‎ 11.5‎ ‎ 13‎ ‎ y1（分钟）‎ ‎ 18‎ ‎ 20‎ ‎ 22‎ ‎ 25‎ ‎ 28‎ ‎（1）求y1关于x的函数表达式；‎ ‎（2）李华骑单车的时间（单位：分钟）也受x的影响，其关系可以用y2=x2﹣11x+78来描述，请问：李华应选择在那一站出地铁，才能使他从文化宫回到家所需的时间最短？并求出最短时间．‎ ‎【解答】解：（1）设y1=kx+b，将（8，18），（9，20），代入得：‎ ‎，‎ 第23页（共23页）‎ 解得：，‎ 故y1关于x的函数表达式为：y1=2x+2；‎ ‎（2）设李华从文化宫回到家所需的时间为y，则 y=y1+y2=2x+2+x2﹣11x+78=x2﹣9x+80，‎ ‎∴当x=9时，y有最小值，ymin==39.5，‎ 答：李华应选择在B站出地铁，才能使他从文化宫回到家所需的时间最短，最短时间为39.5分钟．‎ ‎24．（2017•南宁）如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．‎ ‎（1）求证：△ECF∽△GCE；‎ ‎（2）求证：EG是⊙O的切线；‎ ‎（3）延长AB交GE的延长线于点M，若tanG=，AH=3，求EM的值．‎ ‎【解答】（1）证明：如图1中，‎ ‎∵AC∥EG，‎ 第23页（共23页）‎ ‎∴∠G=∠ACG，‎ ‎∵AB⊥CD，‎ ‎∴=，‎ ‎∴∠CEF=∠ACD，‎ ‎∴∠G=∠CEF，∵∠ECF=∠ECG，‎ ‎∴△ECF∽△GCE．‎ ‎（2）证明：如图2中，连接OE，‎ ‎∵GF=GE，‎ ‎∴∠GFE=∠GEF=∠AFH，‎ ‎∵OA=OE，‎ ‎∴∠OAE=∠OEA，‎ ‎∵∠AFH+∠FAH=90°，‎ ‎∴∠GEF+∠AEO=90°，‎ ‎∴∠GEO=90°，‎ ‎∴GE⊥OE，‎ ‎∴EG是⊙O的切线．‎ ‎（3）解：如图3中，连接OC．设⊙O的半径为r．‎ 第23页（共23页）‎ 在Rt△AHC中，tan∠ACH=tan∠G==，‎ ‎∵AH=3，‎ ‎∴HC=4，‎ 在Rt△HOC中，∵OC=r，OH=r﹣3，HC=4，‎ ‎∴（r﹣3）2+（4）2=r2，‎ ‎∴r=，‎ ‎∵GM∥AC，‎ ‎∴∠CAH=∠M，∵∠OEM=∠AHC，‎ ‎∴△AHC∽△MEO，‎ ‎∴=，‎ ‎∴=，‎ ‎∴EM=．‎ ‎25．（2017•成都）如图1，在平面直角坐标系xOy中，抛物线C：y=ax2+bx+c与x轴相交于A，B两点，顶点为D（0，4），AB=4，设点F（m，0）是x轴的正半轴上一点，将抛物线C绕点F旋转180°，得到新的抛物线C′．‎ ‎（1）求抛物线C的函数表达式；‎ ‎（2）若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围．‎ 第23页（共23页）‎ ‎（3）如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P在抛物线C′上的对应点P′，设M是C上的动点，N是C′上的动点，试探究四边形PMP′N能否成为正方形？若能，求出m的值；若不能，请说明理由．‎ ‎【解答】解：（1）由题意抛物线的顶点C（0，4），A（2，0），设抛物线的解析式为y=ax2+4，‎ 把A（2，0）代入可得a=﹣，‎ ‎∴抛物线C的函数表达式为y=﹣x2+4．‎ ‎（2）由题意抛物线C′的顶点坐标为（2m，﹣4），设抛物线C′的解析式为y=（x﹣2m）2﹣4，‎ 由，消去y得到x2﹣2mx+2m2﹣8=0，‎ 由题意，抛物线C′与抛物线C在y轴的右侧有两个不同的公共点，‎ 则有，解得2＜m＜2，‎ ‎∴满足条件的m的取值范围为2＜m＜2．‎ ‎（3）结论：四边形PMP′N能成为正方形．‎ 理由：1情形1，如图，作PE⊥x轴于E，MH⊥x轴于H．‎ 第23页（共23页）‎ 由题意易知P（2，2），当△PFM是等腰直角三角形时，四边形PMP′N是正方形，‎ ‎∴PF=FM，∠PFM=90°，‎ 易证△PFE≌△FMH，可得PE=FH=2，EF=HM=2﹣m，‎ ‎∴M（m+2，m﹣2），‎ ‎∵点M在y=﹣x2+4上，‎ ‎∴m﹣2=﹣（m+2）2+4，解得m=﹣3或﹣﹣3（舍弃），‎ ‎∴m=﹣3时，四边形PMP′N是正方形．‎ 情形2，如图，四边形PMP′N是正方形，同法可得M（m﹣2，2﹣m），‎ 把M（m﹣2，2﹣m）代入y=﹣x2+4中，2﹣m=﹣（m﹣2）2+4，解得m=6或0（舍弃），‎ ‎∴m=6时，四边形PMP′N是正方形．‎ 第23页（共23页）‎ 第23页（共23页）‎