2014重庆市中考数学试卷A卷 14页

‎2014年重庆市中考数学试卷 ‎（满分150分，考试时间120分钟）‎ 一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的。）‎ ‎1.（2014重庆市A卷，1，4分）实数－17的相反数是（ ）‎ A．17 B． C．－17 D．‎ ‎【答案】A ‎2. （2014重庆市A卷，2，4分）计算的结果是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎3. （2014重庆市A卷，3，4分）在中，a的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎4. （2014重庆市A卷，4，4分）五边形的内角和是（ ）‎ A．180° B．360° C．540° D．600°‎ ‎【答案】C ‎5. （2014重庆市A卷，5，4分）‎2014年1月1日零点，北京、上海、重庆、宁夏的气温分别是－4℃、5℃、6℃、－8℃，当时这四个城市中，气温最低的是（ ）‎ A．北京 B．上海 C．重庆 D．宁夏 ‎【答案】D ‎6. （2014重庆市A卷，6，4分）关于x的方程的解是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎7. 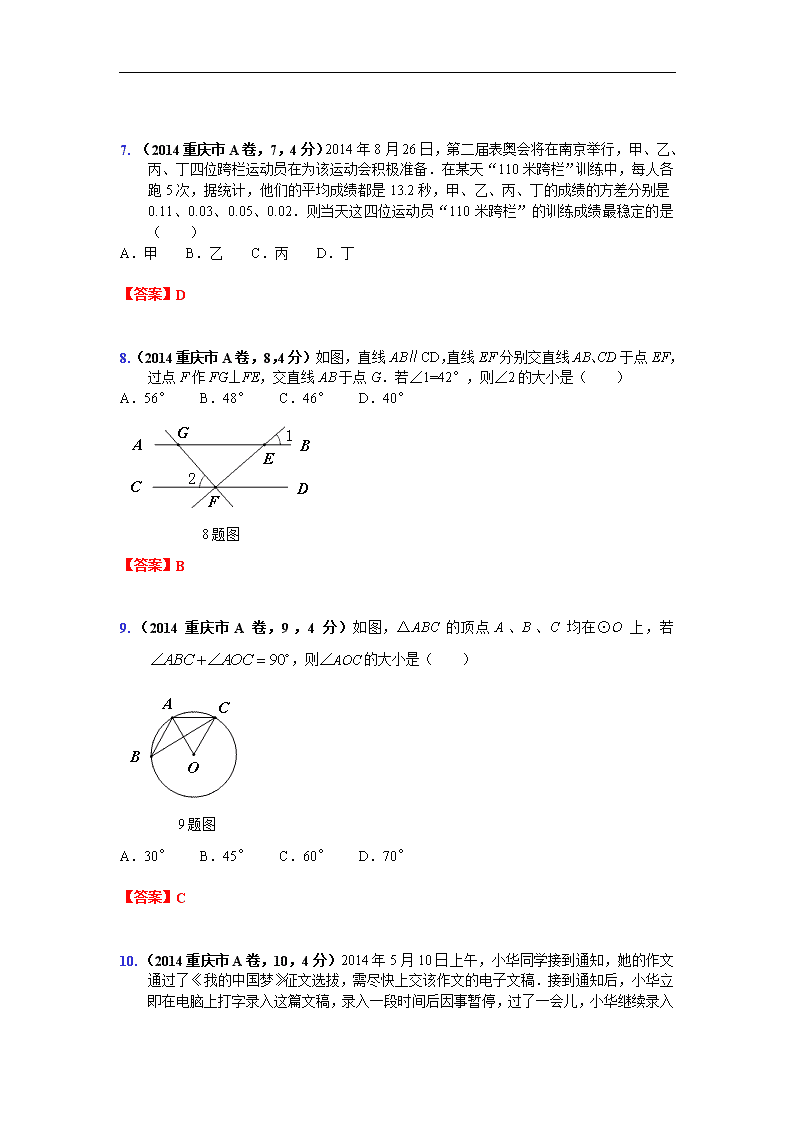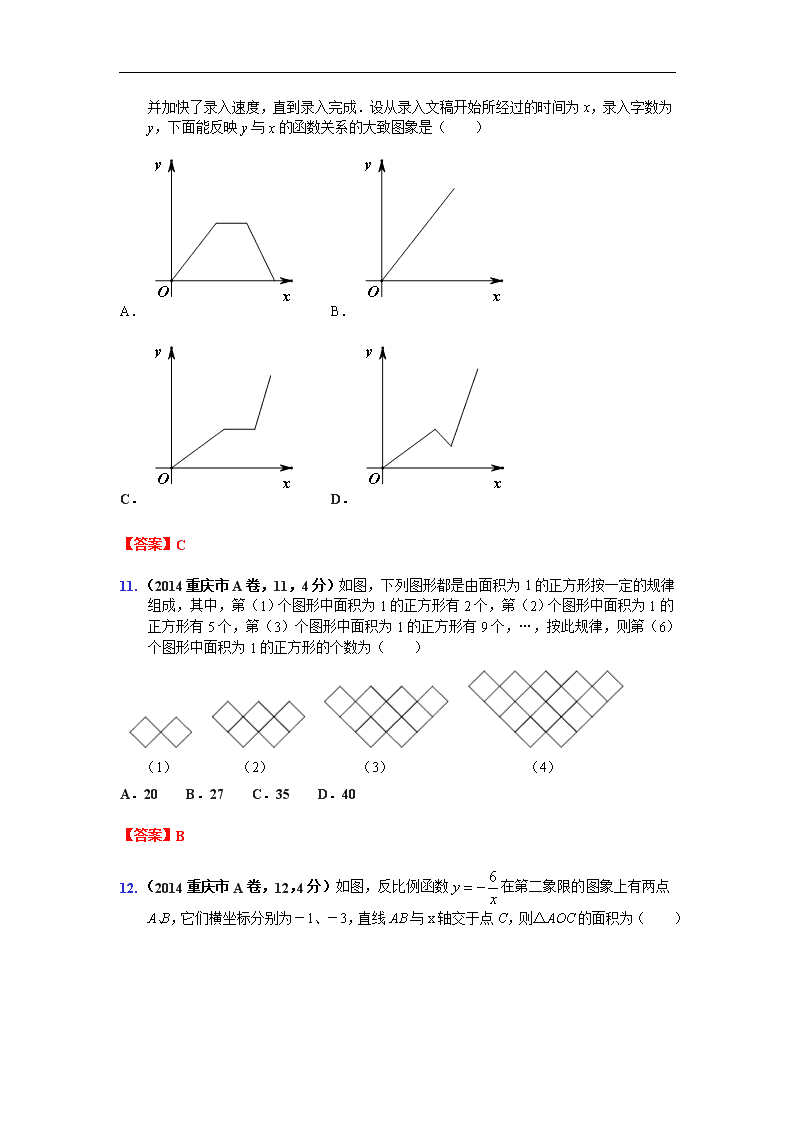（2014重庆市A卷，7，4分）‎2014年8月26日，第二届表奥会将在南京举行，甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备．在某天“110米跨栏”训练中，每人各跑5次，据统计，他们的平均成绩都是13.2秒，甲、乙、丙、丁的成绩的方差分别是0.11、0.03、0.05、0.02．则当天这四位运动员“110米跨栏”的训练成绩最稳定的是（ ）‎ A．甲 B．乙 C．丙 D．丁 ‎【答案】D ‎8.（2014重庆市A卷，8，4分）如图，直线AB∥CD，直线EF分别交直线AB、CD于点EF，过点F作FG⊥FE，交直线AB于点G．若∠1=42°，则∠2的大小是（ ）‎ A．56° B．48° C．46° D．40°‎ ‎8题图 ‎【答案】B ‎9.（2014重庆市A卷，9，4分）如图，△ABC的顶点A、B、C均在⊙O上，若，则∠AOC的大小是（ ）‎ ‎9题图 A．30° B．45° C．60° D．70°‎ ‎【答案】C ‎10. （2014重庆市A卷，10，4分）‎‎2014年5月10日 上午，小华同学接到通知，她的作文通过了《我的中国梦》征文选拔，需尽快上交该作文的电子文稿．接到通知后，小华立即在电脑上打字录入这篇文稿，录入一段时间后因事暂停，过了一会儿，小华继续录入并加快了录入速度，直到录入完成．设从录入文稿开始所经过的时间为x，录入字数为y，下面能反映y与x的函数关系的大致图象是（ ）‎ A． B． ‎ C． D．‎ ‎【答案】C ‎11. （2014重庆市A卷，11，4分）如图，下列图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有5个，第（3）个图形中面积为1的正方形有9个，…，按此规律，则第（6）个图形中面积为1的正方形的个数为（ ）‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎（4）‎ A．20 B．27 C．35 D．40‎ ‎【答案】B ‎12. （2014重庆市A卷，12，4分）如图，反比例函数在第二象限的图象上有两点A、B，它们横坐标分别为－1、－3，直线AB与x轴交于点C，则△AOC的面积为（ ）‎ ‎12题图 A．8 B．10 C．12 D．24‎ ‎【答案】C 二、填空题（本大题共6小题，每小题4分，满分24分.）‎ ‎13. （2014重庆市A卷，13，4分）方程组的解是________．‎ ‎【答案】‎ ‎14. （2014重庆市A卷，14，4分）据有关部门统计，截止到‎2014年5月1日，重庆市私家小轿车已达到563 000辆，将563 000这个数字用科学记数法表示为________．‎ ‎【答案】‎ ‎15. （2014重庆市A卷，15，4分）如图，菱形ABCD中，∠A=60°，BD=7，则菱形ABCD的周长为________．‎ ‎【答案】28‎ ‎16. （2014重庆市A卷，16，4分）如图，△OAB中，OA=OB=4，∠A=30°，AB与⊙O 相切于点C，则图中阴影部分的面积是________．（结果保留π）‎ ‎【答案】‎ ‎17. jscm（2014重庆市A卷，17，4分）从－1，1，2这三个数字中，随机抽取一个数，记为a，那么，使关于x的一次函数的图象与x轴、y轴围成的三角形面积为，且使关于x的不等式组有解的概率为________．‎ ‎【答案】‎ ‎18.jscm（2014重庆市A卷，18，4分）如图，正方形ABCD的边长为6，点O是对角线AC、BD的交点，点E在CD上，且，连接BE．过点C作CF⊥BE，垂足是F，连接OF，则OF的长为________．‎ ‎【答案】‎ 三、解答题（本大题共2小题，每小题7分，共14分，解答应写出文字说明、证明过程或演算步骤）‎ ‎19. （2014重庆市A卷，19，7分）计算：‎ ‎【答案】解：原式=2＋9－1×4＋6 =13‎ ‎20. （2014重庆市A卷，20，7分）如图，△ABC中，AD⊥BC，垂足是D，若BC=14，AD=12，，求的值．‎ ‎【答案】解：∵AD⊥BC，∴，‎ ‎∵，AD=12，∴BD=9‎ ‎∴CD=BC－BD=14－9=5‎ ‎∴在Rt△ADC中，‎ ‎∴‎ 四、解答题（本大题共4小题，每小题10分，共20分，解答应写出文字说明、证明过程或演算步骤）‎ ‎21.（2014重庆市A卷，21，10分）先化简，再求值：，其中x的值为方程的解．‎ ‎【答案】解：原式=‎ ‎=‎ ‎=‎ ‎=‎ ‎=‎ ‎=‎ 解方程得，‎ 当时，原式==‎ ‎22. jscm（2014重庆市A卷，22，10分）为鼓励创业，市政府制定了小型企业的优惠政策，许多小型企业应运而生．某镇统计了该镇今年1～5月新注册小型企业的数量，并将结果绘制成如下两种不完整的统计图：‎ ‎22题图 ‎（1）某镇今年1～5月新注册小型企业一共有________家，请将折线图补充完整；‎ ‎（2）该镇今年3月新注册的小型企业中，只有2家是餐饮企业．现从3月新注册的小型企业中随机抽取2家企业了解其经营状况，请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率．‎ ‎【答案】解：（1）16；补图如下：‎ ‎（2）用表示餐饮企业，表示非餐饮企业，画树状图如下：‎ 由树状图或列表可知，共有12种等可能情况，其中所抽取的企业恰好都是餐饮业的有2种，所以，所抽取的企业恰好都是餐饮企业的概率为 ‎23. （2014重庆市A卷，23，10分）为丰富居民业余生活，某居民区组建筹委会，该筹委会动员居民自愿集资建立一个书刊阅览室，经预算，一共需要筹资30 000元，其中一部分用于购买书桌、书架等设施，另一部分用于购买书刊．‎ ‎（1）筹委会计划，购买书刊的资金不少于购买书桌、书架等设施资金的3倍，问最多用多少资金购买书桌、书架等设施？‎ ‎（2）经初步统计，有200户居民自愿参与集资，那么平均每户需要集资150元．镇政府了解情况后，赠送了一批阅览室设施和书籍，这样，只需参与户集资20 000元．经筹委会进一步宣传，自愿参与的户数在200户的基础上增加了a%（其中a>0），则每户平均集资的资金在150元的基础上减少了，求a的值．‎ ‎【答案】解：（1）设用于购买书桌、书架等设施的资金为x元，由题意，得：‎ 解得，‎ 答：最多花7500元资金购买书桌、书架等设施．‎ ‎（2）由题意，得：‎ 设，则，整理得，‎ 解得（舍），‎ ‎∴，∴‎ ‎24. （2014重庆市A卷，24，10分）如图，△ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E．在△ABC外有一点F，使FA⊥AE，FC⊥BC．‎ ‎（1）求证：BE=CF；‎ ‎（2）在AB上取一点M，使BM=2DE，连接MC，交AD于点N，连接ME．‎ 求证：①ME⊥BC；②DE=DN ‎【答案】证明：如图，（1）∵，，‎ ‎∴，‎ ‎∴‎ 又∵，‎ ‎∴‎ ‎∵，‎ ‎∴，‎ ‎∴‎ ‎∴(ASA)‎ ‎∴‎ ‎（2）①过E作于点G ‎∵，∴△GBE是等腰直角三角形，∴‎ ‎∵，AE平分∠BAD，∴，∴‎ ‎∵，∴，即G是BM的中点 ‎∴GE是BM的垂直平分线，∴EB=EM，∴∠4=∠3=45°‎ ‎∴∠MEB=∠4＋∠3=45°＋45°=90°，即ME⊥BC．‎ ‎②∵AD⊥BC，∴ME∥AD，∴∠5=∠6‎ ‎∵∠1=∠5，∴∠1=∠6，∴AM=EM ‎∵MC=MC，∴Rt△AMC≌Rt△EMC（HL）‎ ‎∴∠7=∠8‎ ‎∵∠BAC=90°，AB=AC，∴∠ACB=45°，∠BAD=∠CAD=45°，‎ ‎∴∠5=∠7=22.5°，AD=CD ‎∵∠ADE=∠CDN=90°，∴△ADE≌△CDN（ASA）‎ ‎∴DE=DN 五、解答题（本大题共2小题，每小题12分，共24分，解答时每小题都必须写出必要的演算过程或推理步骤）‎ ‎25. （2014重庆市A卷，25，12分）如图，抛物线的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．‎ ‎（1）求点A、B、C的坐标；‎ ‎（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，若点P在点Q的左边，当矩形PMNQ的周长最大时，求△AEM的面积；‎ ‎（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作y轴的平行线，与直线AC交于点G（G在点F的上方）．若，求点F的坐标．‎ ‎【答案】解：(1)对 令x=0得，y=3，则C(0，3)‎ 令y=0，得，解得，∴A（－3，0），B（1，0）‎ ‎(2)由得抛物线的对称轴为直线 设点M（x，0），，其中－3＜x＜－1‎ ‎∵P、Q关于直线对称，设Q的横坐标为a，‎ 则，∴‎ ‎∴，‎ ‎∴周长 当时，d取最大值，‎ 此时，M（－2，0），∴‎ 设直线AB解析式为（k≠0），则解得，‎ ‎∴直线AB解析式为 将代入得，∴，∴EM=1‎ ‎∴‎ ‎(3)由（2）知，当矩形PMNQ的周长最大时，，‎ 此时点,与点C重合，∴OQ=3．‎ 将代入，得，‎ ‎∴‎ 如图，过D作DK⊥y轴于K，则DK=1，OK=4‎ ‎∴QK=OK－OQ=4－3=1‎ ‎∴△DKQ是等腰直角三角形，‎ ‎∴‎ 设 则 ‎∵∴，解得 当时，‎ 当时，‎ ‎∴或 ‎26. （2014重庆市A卷，26，12分）已知：如图①，在矩形ABCD中，AB=5，，‎ ‎,垂足是E，点F是点E关于AB的对称点，连接AF、BF．‎ ‎（1）求AE和BE的长；‎ ‎（2）若将△ABF沿着射线BD方向平移，设平移的距离m（平移距离指点B沿BD方向所经过的线段长度），当点F分别平移到线段AB、AD上时，直接写出相应的m的值；‎ ‎（3）如图②，将△ABF绕点B顺时针旋转一个角度α（0°＜α＜180°）．记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P，与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．‎ 图①‎ 图②‎ ‎【答案】解：,‎ 由勾股定理 ‎∵‎ ‎∴‎ 解得 ‎∴‎ ‎(2)当点F在线段AB上时，‎ 当点F在线段AD上时，‎ ‎（3）存在，理由如下：‎ ‎①当DP=DQ时，‎ 若点Q在线段BD的延长线上时，如答图①‎ 有∠Q=∠1，‎ 则 ‎∵‎ ‎∴‎ ‎∴A′Q=A′B=5，∴F′Q=4＋5=9‎ 在Rt△BF′Q中,‎ ‎∴，‎ ‎∴或（舍）‎ ‎②若点Q在线段BD上时，如答图②‎ 有∠1=∠2=∠4‎ ‎∵∠1=∠3，∴∠3=∠4，‎ ‎∵∠3=∠5＋∠A′，∠A′=∠A′BQ，‎ ‎∴∠3=∠5＋∠CBD=∠A′BQ，‎ ‎∴A′Q=A′B=5‎ ‎∴F′Q=5－4=1‎ ‎∴‎ ‎∴‎ 综上所述，存在这样的P、Q两点，使△DPQ为等腰三角形，此时或 答图②‎ 答图①‎