2018中考数学专题复习专题十一几何综合题——专练 3页

专题十一 几何综合题 专练6 几何模型——十字架结构模型 基本经验图形 正方形ABCD中，AM⊥BN，则△ADM≌△BAN；AM=BN 矩形ABCD中，CE⊥BD，则△CDE∽△BCD， ‎ 在△ABC中，AB＝AC，AB⊥AC，①D为中点，②AE⊥BD，③BE：EC＝2：1，④∠ADB＝∠CDE，⑤∠AEB＝∠CED，⑥∠BMC＝135°，⑦，这七个结论中，“知二得五”‎ 正方形中由垂直可利用全等导出相等 长方形中由垂直可利用相似导出边成比例 等腰直角三角形中由垂直利用相似（全等）导出角相等或边成比例（相等）‎ ‎【典例】在Rt△ACB中，AC=4，BC=3，点D为AC上一点，连接BD，E为AB上一点，CE⊥BD，点AD=CD时，求CE的长．‎ ‎【思路分析】CE与AC、BC没有直接关系，可考虑通过相似求线段CE长，又CE⊥BD，可考虑通过矩形内的十字架结构，被成矩形ACBH，延长CE交AH于点G，由“X”字型相似，可得，故需求AG、EG，由矩形内十字架结构可得△BCD∽△CAG，求出AG、EG长即可解决．‎ ‎【解析】过A、B两点作BC、AC平行线，相交于点H，延长CE交AH于点E，由∠CBD+∠BDC=90°，∠ACG+∠BDC=90°，可得∠CBD=∠ACG，所以△BCD∽△CAG，，即，所以AG=，CG=，又△AEG∽BEC，‎ ‎，即，解得CE=．‎ ‎【启示】一般情况下，当矩形、正方形、直角三角形等图形内出现“垂直”情况时，可考虑十字架结构模型，通过相似（或全等）求出线段的长．‎ ‎【针对训练】‎ ‎1．如图，将边长为4的正方形纸片ABCD折叠，使得点A落在CD的中点E处，折痕为FG，点F在AD边上，则折痕FG的长为（ ）‎ ‎ ‎ A．5 B． C． D．‎ ‎2．如图，已知直线与轴、轴分别交于B、A两点，将△AOB沿着AB翻折，使点O落在点D上，当反比例函数经过点D时，则的值为( ).‎ A．4 B． C．5 D． ‎ ‎3．在矩形ABCD中，AB=，BC=2，过D点作DE⊥AC交BC于F点，则的值为（ ）‎ A． B． C． D． ‎ ‎4．如图，在Rt △ABC中，∠ABC＝90°，BA＝BC，点D为BC边上的中点，BE⊥AD于点E，延长BE交AC于点F，则AF：FC的值为 .‎ ‎ ‎ ‎5．如图，把边长为AB＝6，BC＝8的矩形对折，使点B和D重合，则折痕MN的长为 .‎ ‎6．如图，把边长为AB＝，BC＝4且∠B＝45°的平行四边形ABCD对折，使点B和点D重合，则折痕MN的长为 ‎ ‎ ‎ ‎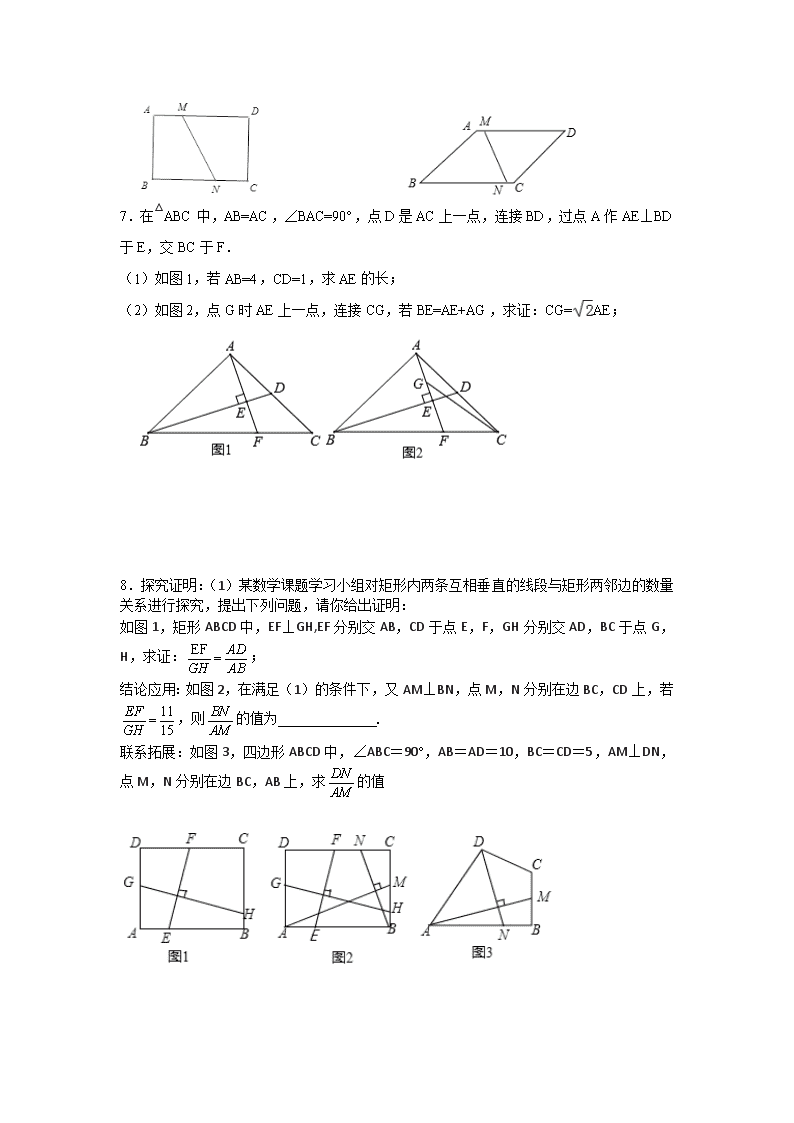7．在△ABC中，AB=AC，∠BAC=90°，点D是AC上一点，连接BD，过点A作AE⊥BD于E，交BC于F．‎ ‎（1）如图1，若AB=4，CD=1，求AE的长；‎ ‎（2）如图2，点G时AE上一点，连接CG，若BE=AE+AG，求证：CG=AE；‎ ‎ ‎ ‎8．探究证明：（1）某数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明：‎ 如图1，矩形ABCD中，EF⊥GH,EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H，求证：；‎ 结论应用：如图2，在满足（1）的条件下，又AM⊥BN，点M，N分别在边BC，CD上，若，则的值为 .‎ 联系拓展：如图3，四边形ABCD中，∠ABC＝90°，AB＝AD＝10，BC＝CD＝5，AM⊥DN，点M，N分别在边BC，AB上，求的值 ‎ ‎