2018中考数学模拟9 10页

‎2018年高中（中专）招生统一考试模拟试卷 数 学（9）‎ ‎ 姓名 班级 考号 ‎ ‎（全卷三个大题，共27个题，共5页；满分150分，考试用时120分钟）‎ 注意事项：‎ 1． 本卷为试题卷，考生必须在答题卷上解题作答，答案书写在答题卷相应位置上，在试题卷、草稿纸上作答无效．‎ 2． 考试结束后，请将试题卷和答题卷一并交回．‎ 一、选择题（每小题3分，共45分） ‎ ‎1、的值等于（ ）‎ A、 B、‎4 C、 D、2‎ ‎2、下列事件中，是确定事件的是( 　 ) . ‎ A.打雷后会下雨 　　　　B.　明天是睛天 C. 1小时等于60分钟 　　D.下雨后有彩虹 ‎3、如图所示的Rt⊿ABC绕直角边AB旋转一周，所得几何体的主视图为（ ）‎ C B A A B C D ‎4、二次函数y=kx-6x+3的图像与X轴有交点，则K值的取值范围是（ ）‎ A.K﹤3 B.K﹤3且K≠‎0 ‎‎ C.K≤3 D.K≤3且K≠0‎ ‎5、在下列图形中既是轴对称图形又是中心对称图形的是（　　）‎ ‎①线段，②角，③等边三角形，④圆，⑤平行四边形，⑥矩形．‎ ‎　‎ A．‎ ‎③④⑥‎ B．‎ ‎①③⑥‎ C．‎ ‎④⑤⑥‎ D．‎ ‎①④⑥‎ ‎6、有理数２的相反数为（ ）‎ ‎（Ａ）　（Ｂ）２　（Ｃ）－２　（Ｄ）０.５‎ ‎7、下列运算正确的是（ ） ‎ A. B. C. 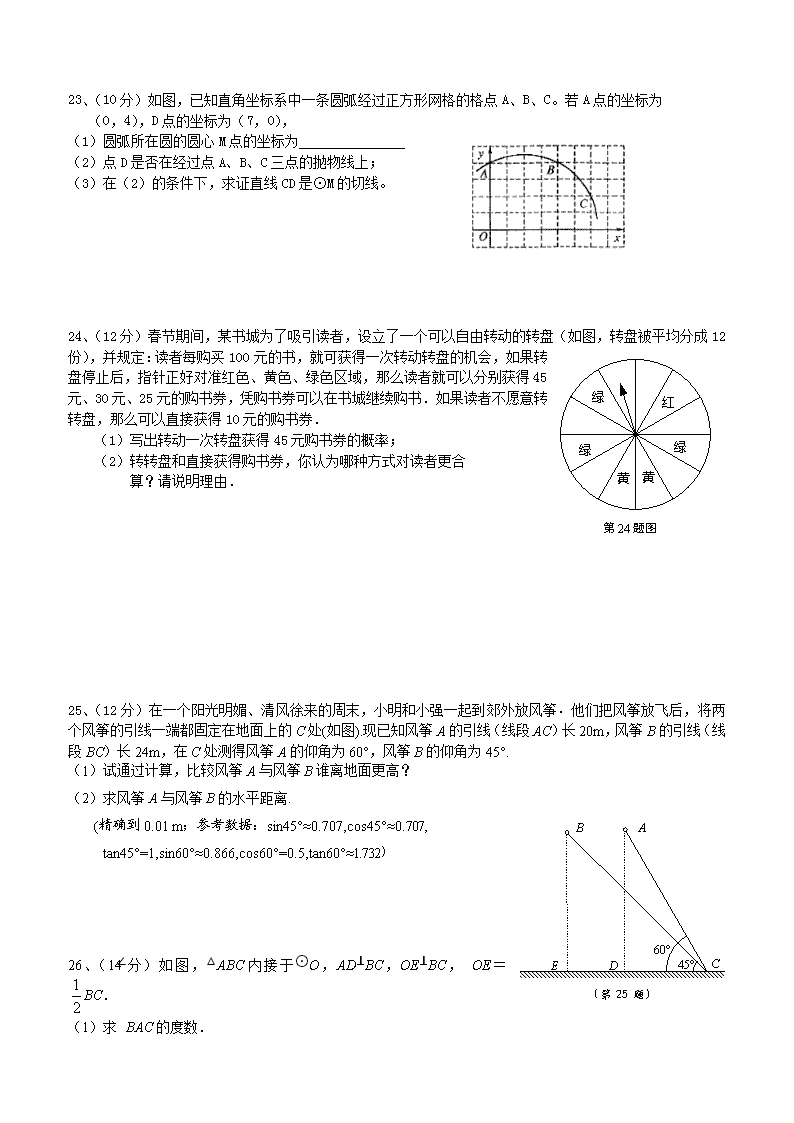D.‎ ‎8、北京市2016年暨“十三五”期间国民经济和社会发展统计公报显示，2016年末，全市共有公共图书馆25个，总藏量44 510 000册．将44 510 000用科学记数法表示应为（ ）‎ A． B． C． D．‎ ‎9、 方程的根是 （ ）‎ Ａ、２　 　Ｂ、４　　 Ｃ、±２　 　　Ｄ、±４‎ ‎（第11题）‎ A B C D O ‎10、在下列图形中，即是轴对称图形，又是中心对称图形的是（ ）‎ A D C B ‎11、如图，已知□ABCD的对角线BD=‎4cm，将□ABCD绕其对称中心O旋转180°，则点D所转过的路径长为( )‎ A．4π cm B．3π cm C．2π cm D．π cm A B C D E 第13题图 ‎12、若△ABC∽△DEF,△DEF与△ABC的相似比为1∶2，则△ABC与△DEF的周长比为( )‎ A.1:2 B.1:4 C.2:1 D.4:1‎ ‎13、如图，在菱形ABCD中，DE⊥AB，，BE=2，‎ 则tan∠DBE的值是( )‎ A． B．‎2 ‎‎ ‎‎ C． D．‎ ‎14、菱形ABCD的边长是5，两条对角线交于O点，且AO、BO的长分别是关于的方程：的根，则的值为（ ）‎ ‎ A、－3 B、‎5 C、5或－3 D、－5或3‎ x y O x=1‎ ‎1‎ ‎-1‎ ‎15、已知二次函数的图象如右图所示，‎ 下列结论: ① ②‎ ‎③ ④的实数)， ‎ 其中正确的结论有( )‎ ‎ A 1个 B．2个 C． 3个 D．4个 二、填空题（每小题5分，共25分）‎ ‎16、在函数中，自变量的取值范围是 .‎ ‎17、已知三角形两边长是方程的两个根，则三角形的第三边的取值范围是 ‎ ‎ ‎ ‎18、从，2，3，…，，20这二十个整数中任意取一个数，这个数是的倍数的概率是 ‎ x ‎10‎ ‎9‎ ‎8‎ ‎7‎ ‎6‎ ‎5‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ A1‎ B1‎ C1‎ A B C y ‎19、如图，已知图中的每个小方格都是边长为1的 小正方形，每个小正方形的顶点称为格点．若△ABC 与△A1B1C1是位似图形，且顶点都在格点上，则位似 中心的坐标是___________．‎ ‎20、已知抛物线与抛物线 的形状相同，顶点在直线 上，‎ 且顶点到轴的距离为5，则此抛物线的解析式为 ‎ 三、解答题（本题85分）‎ ‎21、计算(8分) 2sin45°-|-|-（1-）°+（）-‎ ‎22、（8分）已知实数a满足a2+2a﹣15=0，求﹣÷的值．‎ ‎23、（10分）如图，已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C。若A点的坐标为 ‎（0，4），D点的坐标为（7，0），‎ ‎（1）圆弧所在圆的圆心M点的坐标为 ‎ ‎（2）点D是否在经过点A、B、C三点的抛物线上；‎ ‎（3）在（2）的条件下，求证直线CD是⊙M的切线。‎ 第24题图 绿 绿 黄 黄 绿 红 ‎24、（12分）春节期间，某书城为了吸引读者，设立了一个可以自由转动的转盘（如图，转盘被平均分成12份），并规定：读者每购买100元的书，就可获得一次转动转盘的机会，如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么读者就可以分别获得45元、30元、25元的购书券，凭购书券可以在书城继续购书．如果读者不愿意转转盘，那么可以直接获得10元的购书券．‎ ‎（1）写出转动一次转盘获得45元购书券的概率；‎ ‎（2）转转盘和直接获得购书券，你认为哪种方式对读者更合 算？请说明理由．‎ ‎ ‎ ‎25、（12分）在一个阳光明媚、清风徐来的周末，小明和小强一起到郊外放风筝﹒他们把风筝放飞后，将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线（线段AC）长‎20m，风筝B的引线（线段BC）长‎24m，在C处测得风筝A的仰角为60°，风筝B的仰角为45°.‎ ‎（1）试通过计算，比较风筝A与风筝B谁离地面更高？‎ A B ‎45°‎ ‎60°‎ C E D ‎(第25题)图)‎ ‎（2）求风筝A与风筝B的水平距离.‎ ‎ (精确到‎0.01 m；参考数据：sin45°≈0.707,cos45°≈0.707,‎ tan45°=1,sin60°≈0.866,cos60°=0.5,tan60°≈1.732）‎ ‎26、（14分）如图，△ABC内接于⊙O，AD⊥BC，OE⊥BC， OE＝BC． （1）求∠BAC的度数．‎ ‎ （2）将△ACD沿AC折叠为△ACF，将△ABD沿AB折叠为△ABG，延长FC和GB相交于点H．求证：四边形AFHG是正方形． （3）若BD＝6，CD＝4，求AD的长．‎ A F C D E G H B O ‎　　A F C D E G H B O 　 ‎ ‎27、（16分）如图，在平面直角坐标系中，抛物线=－++，经过A（0，－4）、‎ B（，0）、 C（，0）三点，且-=5．‎ ‎（1）求、的值；‎ ‎（2）在抛物线上求一点D，使得四边形BDCE是以 BC为对角线的菱形；‎ ‎（3）在抛物线上是否存在一点P，使得四边形BPOH 是以OB为对角线的菱形？若存在，求出点P的坐标，‎ 并判断这个菱形是否为正方形？若不存在，请说明理由．‎ ‎ ‎ ‎2018年高中（中专）招生统一考试模拟试卷 ‎ 数 学（9）答题卡 姓名 班级 考号 ‎ ‎（全卷三个大题，共27个小题，共3页；满分150分，考试用时120分钟）‎ 一、选择题（本大题共15小题，每小题只有一个正确先项，每小题3分，满分45分）‎ ‎1.[A][B][C][D] 2.[A][B][C][D] 3.[A][B][C][D] 4.[A][B][C][D] 5.[A][B][C][D]‎ ‎6.[A][B][C][D] 7.[A][B][C][D] 8[A][B][C][D] 9.[A][B][C][D] 10.[A][B][C][D]‎ ‎11.[A][B][C][D] 12.[A][B][C][D] 13[A][B][C][D] 14.[A][B][C][D] 15.[A][B][C][D]‎ 二、填空题（本大题共5小题，每小题5分，满分25分）‎ ‎（16） °．(17) ．（18） 、（19） ．（20） ．‎ 三、解答题（本大题共7小题，满分80分）‎ ‎21、计算(8分) 2sin45°-|-|-（1-）°+（）-‎ ‎22、（8分）已知实数a满足a2+2a﹣15=0，求﹣÷的值．‎ ‎23. 23、（10分）如图，已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C。若A点的坐标为 ‎（0，4），D点的坐标为（7，0），‎ ‎（1）圆弧所在圆的圆心M点的坐标为 ‎ ‎（2）点D是否在经过点A、B、C三点的抛物线上；‎ ‎（3）在（2）的条件下，求证直线CD是⊙M的切线。‎ 第24题图 绿 绿 黄 黄 绿 红 ‎24、（12分）‎ 春节期间，某书城为了吸引读者，设立了一个可以自由转动的转盘（如图，转盘被平均分成12份），并规定：读者每购买100元的书，就可获得一次转动转盘的机会，如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么读者就可以分别获得45元、30元、25元的购书券，凭购书券可以在书城继续购书．如果读者不愿意转转盘，那么可以直接获得10元的购书券．‎ ‎（1）写出转动一次转盘获得45元购书券的概率；‎ ‎（2）转转盘和直接获得购书券，你认为哪种方式对读者更合 算？请说明理由．‎ ‎ ‎ ‎25、（12分）在一个阳光明媚、清风徐来的周末，小明和小强一起到郊外放风筝﹒他们把风筝放飞后，将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线（线段AC）长‎20m，风筝B的引线（线段BC）长‎24m，在C处测得风筝A的仰角为60°，风筝B的仰角为45°.‎ ‎（1）试通过计算，比较风筝A与风筝B谁离地面更高？‎ A B ‎45°‎ ‎60°‎ C E D ‎(第25题)图)‎ ‎（2）求风筝A与风筝B的水平距离.‎ ‎ (精确到‎0.01 m；参考数据：sin45°≈0.707,cos45°≈0.707,‎ tan45°=1,sin60°≈0.866,cos60°=0.5,tan60°≈1.732）‎ ‎26、（14分）如图，△ABC内接于⊙O，AD⊥BC，OE⊥BC， OE＝BC． （1）求∠BAC的度数． （2）将△ACD沿AC折叠为△ACF，将△ABD沿AB折叠为△ABG，延长FC和GB相交于点H．求证：四边形AFHG是正方形． （3）若BD＝6，CD＝4，求AD的长．‎ A F C D E G H B O ‎　　A F C D E G H B O 　 ‎ ‎27、（16分）如图，在平面直角坐标系中，抛物线=－++，经过A（0，－4）、‎ B（，0）、 C（，0）三点，且-=5．‎ ‎（1）求、的值；‎ ‎（2）在抛物线上求一点D，使得四边形BDCE是以 BC为对角线的菱形；‎ ‎（3）在抛物线上是否存在一点P，使得四边形BPOH 是以OB为对角线的菱形？若存在，求出点P的坐标，‎ 并判断这个菱形是否为正方形？若不存在，请说明理由．‎ ‎ ‎ ‎ ‎ ‎2018年高中（中专）招生统一考试模拟试卷 数 学（9）参考答案：‎ 一、BCCDD CCBDC CCBAB 二、（16） (17) (18) （19）（9，0）‎ ‎ （20）y=x2--2x+6 或y=x2--2x--4 或y=--x2+2x+4 或y=--x2+2x--6‎ 三、21、 22、 23、（1）(2,0) （2分）‎ ‎（2）由A（0，4），可得小正方形的边长为1，从而B（4，4）、C（6，2）‎ ‎ 　设经过点A、B、C的抛物线的解析式为 ‎ 依题意，解得 ‎ 所以经过点A、B、C的抛物线的解析式为 ‎ ‎ 把点D（7，0）的横坐标代入上述解析式，得 ‎ 所以点D不在经过A、B、C的抛物线上 （3分）‎ ‎（3）设过C点与x轴垂直的直线与x轴的交点为E，连结MC，作直线CD。‎ ‎ 所以CE＝2，ME＝4，ED＝1，MD＝5 在Rt△CEM中，∠CEM＝90°‎ ‎ 所以 在Rt△CED中，∠CED＝90°‎ ‎ 所以 所以 ‎ 所以∠MCE＝90° 因为MC为半径， 所以直线CD是⊙M的切线　　（３分）‎ ‎24、解：（1）P（获得45元购书券） = ； 　（４分） （2）（元）.‎ ‎∵15元＞10元， 　　 ∴转转盘对读者更合算　　　　（４分）‎ ‎25、（1）分别过A，B作地面的垂线，垂足分别为D，E．‎ ‎ 在Rt△ADC中，∵AC﹦20，∠ACD﹦60°，∴AD﹦20×sin 60°﹦10≈‎‎17.32m ‎ 在Rt△BEC中，∵BC﹦24，∠BEC﹦45°，∴BE﹦24×sin 45°﹦12≈16.97 ‎ ‎ ∵17.32>16.97　　 ∴风筝A比风筝B离地面更高． 　　（４分）‎ ‎ （2）在Rt△ADC中，　∵AC﹦20，∠ACD﹦60°，　∴DC﹦20×cos 60°﹦‎‎10 m ‎ 在Rt△BEC中，　∵BC﹦24，∠BEC﹦45°，∴EC﹦BC≈‎‎16.97 m ‎ ∴EC－DC≈16.97－10﹦‎6.97m 即风筝A与风筝B的水平距离约为‎6.97m．（４分）‎ ‎26、（1）连结OB和OC．∵　OE⊥BC，∴　BE＝CE． ∵　OE＝BC，∴　∠BOC＝90°，∴　∠BAC＝45°　　　　（３分）‎ ‎（2）∵　AD⊥BC，∴　∠ADB＝∠ADC＝90°． 由折叠可知，AG＝AF＝AD，∠AGH＝∠AFH＝90°， ∠BAG＝∠BAD，∠CAF＝∠CAD，∴　∠BAG＋∠CAF＝∠BAD＋∠CAD＝∠BAC＝45°． ∴∠GAF＝∠BAG＋∠CAF＋∠BAC＝90° ∴四边形AFHG是正方形．　　　（3分） （3）由（2）得，∠BHC＝90°，GH＝HF＝AD，GB＝BD＝6，CF＝CD＝4． 　　设AD的长为x，则　BH＝GH－GB＝x－6，CH＝HF－CF＝x－4．　　‎ 在Rt△BCH中，BH2＋CH2＝BC2，∴　（x－6）2＋（x－4）2＝102． 解得，x1=12，x2＝－2（不合题意，舍去）．∴　AD＝12．　　（3分）‎ ‎27、（1）解法一：∵抛物线=－++经过点A（0，－4），∴=－4 ‎ 又由题意可知，、是方程－++=0的两个根，‎ ‎∴+=， =－=6‎ 由已知得（-）=25又（-）=（+）－4=－24‎ ‎∴ －24=25 ，解得=± ‎ 当=时，抛物线与轴的交点在轴的正半轴上，不合题意，舍去．∴=－． ‎ 解法二：∵、是方程－++c=0的两个根，‎ 即方程2－3+12=0的两个根．∴=，‎ ‎∴－==5， 解得 =±（以下与解法一相同．） 　（３分） ‎ ‎（2）∵四边形BDCE是以BC为对角线的菱形，根据菱形的性质，点D必在抛物线的对称轴上， 又∵=－－－4=－（+）+ ∴抛物线的顶点（－，）即为所求的点D．　　　　（３分）‎ ‎（3）∵四边形BPOH是以OB为对角线的菱形，点B的坐标为（－6，0），‎ 根据菱形的性质，点P必是直线=-3与 抛物线=－--4的交点， ‎ ‎∴当=－3时，=－×（－3）－×（－3）－4=4， ‎ ‎∴在抛物线上存在一点P（－3，4），使得四边形BPOH为菱形．‎ 四边形BPOH不能成为正方形，因为如果四边形BPOH为正方形，点P的坐标只能是 ‎（－3，3），但这一点不在抛物线上．　　　　（４分）‎