资阳市2016年中考数学卷 23页

‎2016年四川省资阳市中考数学试卷 ‎　‎ 一、选择题．（本大题共10小题，每小题3分，共30分）‎ ‎1．﹣2的倒数是（　　）‎ A．﹣B． C．﹣2 D．2‎ ‎2．下列运算正确的是（　　）‎ A．x4+x2=x6B．x2•x3=x6C．（x2）3=x6D．x2﹣y2=（x﹣y）2‎ ‎3．如图是一个正方体纸盒的外表面展开图，则这个正方体是（　　）‎ A． B． C． D．‎ ‎4．世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有0.000000076克，将数0.000000076用科学记数法表示为（　　）‎ A．7.6×10﹣9B．7.6×10﹣8C．7.6×109D．7.6×108‎ ‎5．的运算结果应在哪两个连续整数之间（　　）‎ A．2和3 B．3和4 C．4和5 D．5和6‎ ‎6．我市某中学九年级（1）班开展“阳光体育运动”，决定自筹资金为班级购买体育器材，全班50名同学筹款情况如下表：‎ 筹款金额（元）‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎25‎ ‎30‎ 人数 ‎3‎ ‎7‎ ‎11‎ ‎11‎ ‎13‎ ‎5‎ 则该班同学筹款金额的众数和中位数分别是（　　）‎ A．11，20 B．25，11 C．20，25 D．25，20‎ ‎7．如图，两个三角形的面积分别是9，6，对应阴影部分的面积分别是m，n，则m﹣n等于（　　）‎ A．2 B．3 C．4 D．无法确定 ‎8．在Rt△ABC中，∠ACB=90°，AC=2，以点B为圆心，BC的长为半径作弧，交AB于点D，若点D为AB的中点，则阴影部分的面积是（　　）‎ A．2﹣π B．4﹣π C．2﹣π D．π ‎9．如图，矩形ABCD与菱形EFGH的对角线均交于点O，且EG∥BC，将矩形折叠，使点C与点O重合，折痕MN恰好过点G若AB=，EF=2，∠H=120°，则DN的长为（　　）‎ A． B． C．﹣D．2﹣‎ ‎10．已知二次函数y=x2+bx+c与x轴只有一个交点，且图象过A（x1，m）、B（x1+n，m）两点，则m、n的关系为（　　）‎ A．m=n B．m=n C．m=n2D．m=n2‎ ‎　‎ 二、填空题．（本大题共6小题，每小题3分，共18分）‎ ‎11．若代数式有意义，则x的取值范围是　　　　　　．‎ ‎12．如图，AC是正五边形ABCDE的一条对角线，则∠ACB=　　　　　　．‎ ‎13．已知关于x的方程mx+3=4的解为x=1，则直线y=（m﹣2）x﹣3一定不经过第　　　　　　象限．‎ ‎14．如图，在3×3的方格中，A、B、C、D、E、F分别位于格点上，从C、D、E、F四点中任取一点，与点A、B为顶点作三角形，则所作三角形为等腰三角形的概率是　　　　　　．‎ ‎15．设一列数中相邻的三个数依次为m、n、p，且满足p=m2﹣n，若这列数为﹣1，3，﹣2，a，﹣7，b…，则b=　　　　　　．‎ ‎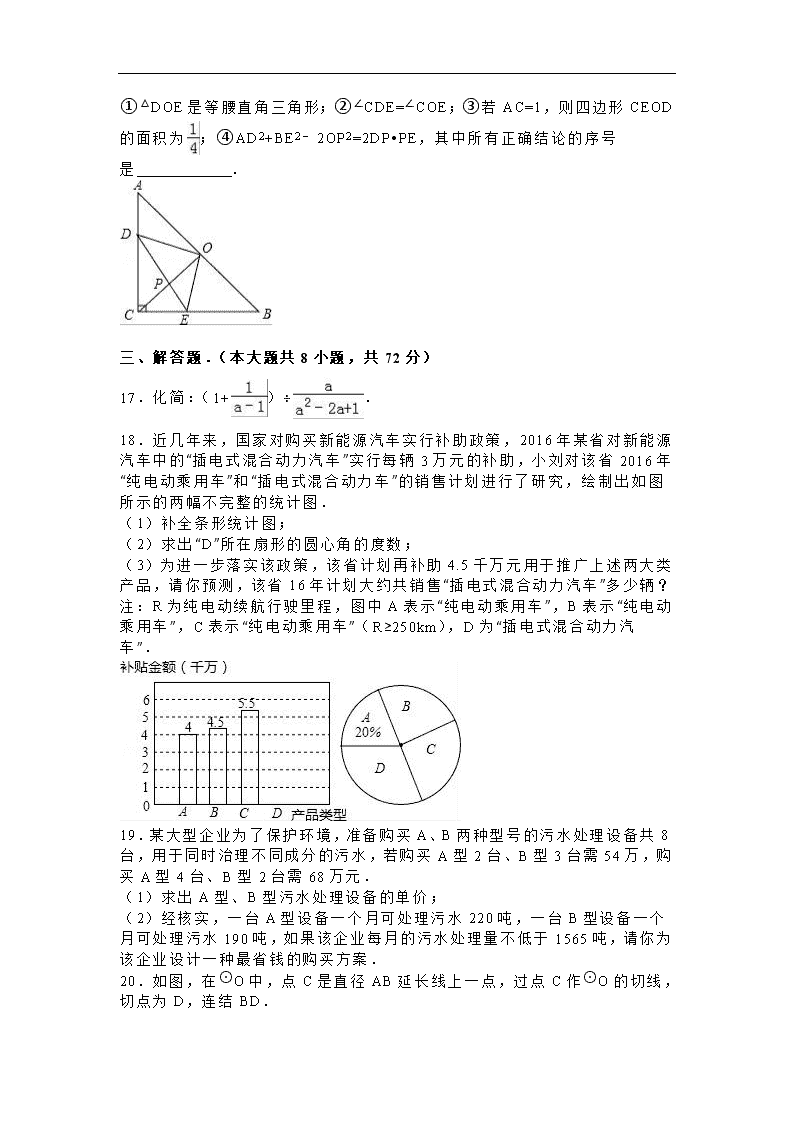16．如图，在等腰直角△ABC中，∠ACB=90°，CO⊥AB于点O，点D、E分别在边AC、BC上，且AD=CE，连结DE交CO于点P，给出以下结论：‎ ‎①△DOE是等腰直角三角形；②∠CDE=∠COE；③若AC=1，则四边形CEOD的面积为；④AD2+BE2﹣2OP2=2DP•PE，其中所有正确结论的序号是　　　　　　．‎ ‎　‎ 三、解答题．（本大题共8小题，共72分）‎ ‎17．化简：（1+）÷．‎ ‎18．近几年来，国家对购买新能源汽车实行补助政策，2016年某省对新能源汽车中的“插电式混合动力汽车”实行每辆3万元的补助，小刘对该省2016年“纯电动乘用车”和“插电式混合动力车”的销售计划进行了研究，绘制出如图所示的两幅不完整的统计图．‎ ‎（1）补全条形统计图；‎ ‎（2）求出“D”所在扇形的圆心角的度数；‎ ‎（3）为进一步落实该政策，该省计划再补助4.5千万元用于推广上述两大类产品，请你预测，该省16年计划大约共销售“插电式混合动力汽车”多少辆？‎ 注：R为纯电动续航行驶里程，图中A表示“纯电动乘用车”，B表示“纯电动乘用车”，C表示“纯电动乘用车”（R≥250km），D为“插电式混合动力汽车”．‎ ‎19．某大型企业为了保护环境，准备购买A、B两种型号的污水处理设备共8台，用于同时治理不同成分的污水，若购买A型2台、B型3台需54万，购买A型4台、B型2台需68万元．‎ ‎（1）求出A型、B型污水处理设备的单价；‎ ‎（2）经核实，一台A型设备一个月可处理污水220吨，一台B型设备一个月可处理污水190吨，如果该企业每月的污水处理量不低于1565吨，请你为该企业设计一种最省钱的购买方案．‎ ‎20．如图，在⊙O中，点C是直径AB延长线上一点，过点C作⊙O的切线，切点为D，连结BD．‎ ‎（1）求证：∠A=∠BDC；‎ ‎（2）若CM平分∠ACD，且分别交AD、BD于点M、N，当DM=1时，求MN的长．‎ ‎21．如图，在平行四边形ABCD中，点A、B、C的坐标分别是（1，0）、（3，1）、（3，3），双曲线y=（k≠0，x＞0）过点D．‎ ‎（1）求双曲线的解析式；‎ ‎（2）作直线AC交y轴于点E，连结DE，求△CDE的面积．‎ ‎22．如图，“中国海监50”正在南海海域A处巡逻，岛礁B上的中国海军发现点A在点B的正西方向上，岛礁C上的中国海军发现点A在点C的南偏东30°方向上，已知点C在点B的北偏西60°方向上，且B、C两地相距120海里．‎ ‎（1）求出此时点A到岛礁C的距离；‎ ‎（2）若“中海监50”从A处沿AC方向向岛礁C驶去，当到达点A′时，测得点B在A′的南偏东75°的方向上，求此时“中国海监50”的航行距离．（注：结果保留根号）‎ ‎23．在Rt△ABC中，∠C=90°，Rt△ABC绕点A顺时针旋转到Rt△ADE的位置，点E在斜边AB上，连结BD，过点D作DF⊥AC于点F．‎ ‎（1）如图1，若点F与点A重合，求证：AC=BC；‎ ‎（2）若∠DAF=∠DBA，‎ ‎①如图2，当点F在线段CA的延长线上时，判断线段AF与线段BE的数量关系，并说明理由；‎ ‎②当点F在线段CA上时，设BE=x，请用含x的代数式表示线段AF．‎ ‎24．已知抛物线与x轴交于A（6，0）、B（﹣，0）两点，与y轴交于点C，过抛物线上点M（1，3）作MN⊥x轴于点N，连接OM．‎ ‎（1）求此抛物线的解析式；‎ ‎（2）如图1，将△OMN沿x轴向右平移t个单位（0≤t≤5）到△O′M′N′的位置，MN′、M′O′与直线AC分别交于点E、F．‎ ‎①当点F为M′O′的中点时，求t的值；‎ ‎②如图2，若直线M′N′与抛物线相交于点G，过点G作GH∥M′O′交AC于点H，试确定线段EH是否存在最大值？若存在，求出它的最大值及此时t的值；若不存在，请说明理由．‎ ‎　‎ ‎2016年四川省资阳市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题．（本大题共10小题，每小题3分，共30分）‎ ‎1．﹣2的倒数是（　　）‎ A．﹣B． C．﹣2 D．2‎ ‎【考点】倒数．‎ ‎【分析】根据倒数的定义即可求解．‎ ‎【解答】解：﹣2的倒数是﹣．‎ 故选：A．‎ ‎　‎ ‎2．下列运算正确的是（　　）‎ A．x4+x2=x6B．x2•x3=x6C．（x2）3=x6D．x2﹣y2=（x﹣y）2‎ ‎【考点】幂的乘方与积的乘方；合并同类项；同底数幂的乘法；因式分解-运用公式法．‎ ‎【分析】根据合并同类项法则、同底数幂的乘法法则、积的乘方法则和公式法进行因式分解对各个选项进行判断即可．‎ ‎【解答】解：x4与x2不是同类项，不能合并，A错误；‎ x2•x3=x5，B错误；‎ ‎（x2）3=x6，C正确；‎ x2﹣y2=（x+y）（x﹣y），D错误，‎ 故选：C．‎ ‎　‎ ‎3．如图是一个正方体纸盒的外表面展开图，则这个正方体是（　　）‎ A． B． C． D．‎ ‎【考点】几何体的展开图．‎ ‎【分析】根据几何体的展开图先判断出实心圆点与空心圆点的关系，进而可得出结论．‎ ‎【解答】解：∵由图可知，实心圆点与空心圆点一定在紧相邻的三个侧面上，‎ ‎∴C符合题意．‎ 故选C．‎ ‎　‎ ‎4．世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有0.000000076克，将数0.000000076用科学记数法表示为（　　）‎ A．7.6×10﹣9B．7.6×10﹣8C．7.6×109D．7.6×108‎ ‎【考点】科学记数法—表示较小的数．‎ ‎【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．‎ ‎【解答】解：将0.000000076用科学记数法表示为7.6×10﹣8，‎ 故选：B．‎ ‎　‎ ‎5．的运算结果应在哪两个连续整数之间（　　）‎ A．2和3 B．3和4 C．4和5 D．5和6‎ ‎【考点】估算无理数的大小．‎ ‎【分析】根据无理数的大小比较方法得到＜＜，即可解答．‎ ‎【解答】解：∵＜＜，‎ 即5＜＜6，‎ ‎∴的运算结果应在5和6两个连续整数之间．‎ 故选：D．‎ ‎　‎ ‎6．我市某中学九年级（1）班开展“阳光体育运动”，决定自筹资金为班级购买体育器材，全班50名同学筹款情况如下表：‎ 筹款金额（元）‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎25‎ ‎30‎ 人数 ‎3‎ ‎7‎ ‎11‎ ‎11‎ ‎13‎ ‎5‎ 则该班同学筹款金额的众数和中位数分别是（　　）‎ A．11，20 B．25，11 C．20，25 D．25，20‎ ‎【考点】众数；中位数．‎ ‎【分析】中位数是一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；众数是一组数据中出现次数最多的数据．‎ ‎【解答】解：在这一组数据中25元是出现次数最多的，故众数是25元；‎ 将这组数据已从小到大的顺序排列，处于中间位置的两个数是20、20，那么由中位数的定义可知，这组数据的中位数是20；‎ 故选：D．‎ ‎　‎ ‎7．如图，两个三角形的面积分别是9，6，对应阴影部分的面积分别是m，n，则m﹣n等于（　　）‎ A．2 B．3 C．4 D．无法确定 ‎【考点】三角形的面积．‎ ‎【分析】设空白出的面积为x，根据题意列出关系式，相减即可求出m﹣n的值．‎ ‎【解答】解：设空白出图形的面积为x，‎ 根据题意得：m+x=9，n+x=6，‎ 则m﹣n=9﹣6=3．‎ 故选B．‎ ‎　‎ ‎8．在Rt△ABC中，∠ACB=90°，AC=2，以点B为圆心，BC的长为半径作弧，交AB于点D，若点D为AB的中点，则阴影部分的面积是（　　）‎ A．2﹣π B．4﹣π C．2﹣π D．π ‎【考点】扇形面积的计算．‎ ‎【分析】根据点D为AB的中点可知BC=BD=AB，故可得出∠A=30°，∠B=60°，再由锐角三角函数的定义求出BC的长，根据S阴影=S△ABC﹣S扇形CBD即可得出结论．‎ ‎【解答】解：∵D为AB的中点，‎ ‎∴BC=BD=AB，‎ ‎∴∠A=30°，∠B=60°．‎ ‎∵AC=2，‎ ‎∴BC=AC•tan30°=2•=2，‎ ‎∴S阴影=S△ABC﹣S扇形CBD=×2×2﹣=2﹣π．‎ 故选A．‎ ‎　‎ ‎9．如图，矩形ABCD与菱形EFGH的对角线均交于点O，且EG∥BC，将矩形折叠，使点C与点O重合，折痕MN恰好过点G若AB=，EF=2，∠H=120°，则DN的长为（　　）‎ A． B． C．﹣D．2﹣‎ ‎【考点】矩形的性质；菱形的性质；翻折变换（折叠问题）．‎ ‎【分析】延长EG交DC于P点，连接GC、FH，则△GCP为直角三角形，证明四边形OGCM为菱形，则可证OC=OM=CM=OG=，由勾股定理求得GP的值，再由梯形的中位线定理CM+DN=2GP，即可得出答案．‎ ‎【解答】解：长EG交DC于P点，连接GC、FH；如图所示：‎ 则CP=DP=CD=，△GCP为直角三角形，‎ ‎∵四边形EFGH是菱形，∠EHG=120°，‎ ‎∴GH=EF=2，∠OHG=60°，EG⊥FH，‎ ‎∴OG=GH•sin60°=2×=，‎ 由折叠的性质得：CG=OG=，OM=CM，∠MOG=∠MCG，‎ ‎∴PG==，‎ ‎∵OG∥CM，‎ ‎∴∠MOG+∠OMC=180°，‎ ‎∴∠MCG+∠OMC=180°，‎ ‎∴OM∥CG，‎ ‎∴四边形OGCM为平行四边形，‎ ‎∵OM=CM，‎ ‎∴四边形OGCM为菱形，‎ ‎∴CM=OG=，‎ 根据题意得：PG是梯形MCDN的中位线，‎ ‎∴DN+CM=2PG=，‎ ‎∴DN=﹣；‎ 故选：C．‎ ‎　‎ ‎10．已知二次函数y=x2+bx+c与x轴只有一个交点，且图象过A（x1，m）、B（x1+n，m）两点，则m、n的关系为（　　）‎ A．m=n B．m=n C．m=n2D．m=n2‎ ‎【考点】抛物线与x轴的交点．‎ ‎【分析】由“抛物线y=x2+bx+c与x轴只有一个交点”推知x=﹣时，y=0．且b2﹣4c=0，即b2=4c，其次，根据抛物线对称轴的定义知点A、B关于对称轴对称，故A（﹣﹣，m），B（﹣+，m）；最后，根据二次函数图象上点的坐标特征即可得出结论．‎ ‎【解答】解：∵抛物线y=x2+bx+c与x轴只有一个交点，‎ ‎∴当x=﹣时，y=0．且b2﹣4c=0，即b2=4c．‎ 又∵点A（x1，m），B（x1+n，m），‎ ‎∴点A、B关于直线x=﹣对称，‎ ‎∴A（﹣﹣，m），B（﹣+，m），‎ 将A点坐标代入抛物线解析式，得m=（﹣﹣）2+（﹣﹣）b+c，即m=﹣+c，‎ ‎∵b2=4c，‎ ‎∴m=n2，‎ 故选D．‎ ‎　‎ 二、填空题．（本大题共6小题，每小题3分，共18分）‎ ‎11．若代数式有意义，则x的取值范围是　x≧2　．‎ ‎【考点】二次根式有意义的条件．‎ ‎【分析】根据式子有意义的条件为a≥0得到x﹣2≥0，然后解不等式即可．‎ ‎【解答】解：∵代数式有意义，‎ ‎∴x﹣2≥0，‎ ‎∴x≥2．‎ 故答案为x≥2．‎ ‎　‎ ‎12．如图，AC是正五边形ABCDE的一条对角线，则∠ACB=　36°　．‎ ‎【考点】多边形内角与外角．‎ ‎【分析】由正五边形的性质得出∠B=108°，AB=CB，由等腰三角形的性质和三角形内角和定理即可得出结果．‎ ‎【解答】解：∵五边形ABCDE是正五边形，‎ ‎∴∠B=108°，AB=CB，‎ ‎∴∠ACB=÷2=36°；‎ 故答案为：36°．‎ ‎　‎ ‎13．已知关于x的方程mx+3=4的解为x=1，则直线y=（m﹣2）x﹣3一定不经过第　一　象限．‎ ‎【考点】一次函数与一元一次方程．‎ ‎【分析】关于x的方程mx+3=4的解为x=1，于是得到m+3=4，求得m=1，得到直线y=﹣x﹣3，于是得到结论．‎ ‎【解答】解：∵关于x的方程mx+3=4的解为x=1，‎ ‎∴m+3=4，‎ ‎∴m=1，‎ ‎∴直线y=（m﹣2）x﹣3为直线y=﹣x﹣3，‎ ‎∴直线y=（m﹣2）x﹣3一定不经过第一象限，‎ 故答案为：一．‎ ‎　‎ ‎14．如图，在3×3的方格中，A、B、C、D、E、F分别位于格点上，从C、D、E、F四点中任取一点，与点A、B为顶点作三角形，则所作三角形为等腰三角形的概率是　　．‎ ‎【考点】概率公式；等腰三角形的判定．‎ ‎【分析】根据从C、D、E、F四个点中任意取一点，一共有4种可能，选取D、C、F时，所作三角形是等腰三角形，即可得出答案．‎ ‎【解答】解：根据从C、D、E、F四个点中任意取一点，一共有4种可能，选取D、C、F时，所作三角形是等腰三角形，‎ 故P（所作三角形是等腰三角形）=；‎ 故答案为：．‎ ‎　‎ ‎15．设一列数中相邻的三个数依次为m、n、p，且满足p=m2﹣n，若这列数为﹣1，3，﹣2，a，﹣7，b…，则b=　128　．‎ ‎【考点】规律型：数字的变化类．‎ ‎【分析】根据题意求出a，再代入关系式即可得出b的值．‎ ‎【解答】解：根据题意得：a=32﹣（﹣2）=11，‎ 则b=112﹣（﹣7）=128．‎ 故答案为：128．‎ ‎　‎ ‎16．如图，在等腰直角△ABC中，∠ACB=90°，CO⊥AB于点O，点D、E分别在边AC、BC上，且AD=CE，连结DE交CO于点P，给出以下结论：‎ ‎①△DOE是等腰直角三角形；②∠CDE=∠COE；③若AC=1，则四边形CEOD的面积为；④AD2+BE2﹣2OP2=2DP•PE，其中所有正确结论的序号是　①②③④　．‎ ‎【考点】勾股定理；四点共圆．‎ ‎【分析】①正确．由ADO≌△CEO，推出DO=OE，∠AOD=∠COE，由此即可判断．‎ ‎②正确．由D、C、E、O四点共圆，即可证明．‎ ‎③正确．由S△ABC=×1×1=，S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC=S△ABC即可解决问题．‎ ‎④正确．由D、C、E、O四点共圆，得OP•PC=DP•PE，所以2OP2+2DP•PE=2OP2+2OP•PC=2OP（OP+PC）=2OP•OC，由△OPE∽△OEC，得到=，即可得到2OP2+2DP•PE=2OE2=DE2=CD2+CE2，由此即可证明．‎ ‎【解答】解：①正确．如图，∵∠ACB=90°，AC=BC，CO⊥AB ‎∴AO=OB=OC，∠A=∠B=∠ACO=∠BCO=45°，‎ 在△ADO和△CEO中，‎ ‎，‎ ‎∴△ADO≌△CEO，‎ ‎∴DO=OE，∠AOD=∠COE，‎ ‎∴∠AOC=∠DOE=90°，‎ ‎∴△DOE是等腰直角三角形．故①正确．‎ ‎②正确．∵∠DCE+∠DOE=180°，‎ ‎∴D、C、E、O四点共圆，‎ ‎∴∠CDE=∠COE，故②正确．‎ ‎③正确．∵AC=BC=1，‎ ‎∴S△ABC=×1×1=，S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC=S△ABC=，‎ 故③正确．‎ ‎④正确．∵D、C、E、O四点共圆，‎ ‎∴OP•PC=DP•PE，‎ ‎∴2OP2+2DP•PE=2OP2+2OP•PC=2OP（OP+PC）=2OP•OC，‎ ‎∵∠OEP=∠DCO=∠OCE=45°，∠POE=∠COE，‎ ‎∴△OPE∽△OEC，‎ ‎∴=，‎ ‎∴OP•OC=OE2，‎ ‎∴2OP2+2DP•PE=2OE2=DE2=CD2+CE2，‎ ‎∵CD=BE，CE=AD，‎ ‎∴AD2+BE2=2OP2+2DP•PE，‎ ‎∴AD2+BE2﹣2OP2=2DP•PE．‎ 故④正确．‎ ‎　‎ 三、解答题．（本大题共8小题，共72分）‎ ‎17．化简：（1+）÷．‎ ‎【考点】分式的混合运算．‎ ‎【分析】首先把括号内的式子通分相加，把除法转化为乘法，然后进行乘法运算即可．‎ ‎【解答】解：原式=÷‎ ‎=•‎ ‎=a﹣1．‎ ‎　‎ ‎18．近几年来，国家对购买新能源汽车实行补助政策，2016年某省对新能源汽车中的“插电式混合动力汽车”实行每辆3万元的补助，小刘对该省2016年“纯电动乘用车”和“插电式混合动力车”的销售计划进行了研究，绘制出如图所示的两幅不完整的统计图．‎ ‎（1）补全条形统计图；‎ ‎（2）求出“D”所在扇形的圆心角的度数；‎ ‎（3）为进一步落实该政策，该省计划再补助4.5千万元用于推广上述两大类产品，请你预测，该省16年计划大约共销售“插电式混合动力汽车”多少辆？‎ 注：R为纯电动续航行驶里程，图中A表示“纯电动乘用车”，B表示“纯电动乘用车”，C表示“纯电动乘用车”（R≥250km），D为“插电式混合动力汽车”．‎ ‎【考点】条形统计图；用样本估计总体；扇形统计图．‎ ‎【分析】（1）首先由A的数目和其所占的百分比可求出总数，进而可求出D的数目，问题得解；‎ ‎（2）由D的数目先求出它所占的百分比，再用百分比乘以360°，即可解答；‎ ‎（3）计算出补贴D类产品的总金额，再除以每辆车的补助可得车的数量．‎ ‎【解答】解：（1）补贴总金额为：4÷20%=20（千万元），‎ 则D类产品补贴金额为：20﹣4﹣4.5﹣5.5=6（千万元），补全条形图如图：‎ ‎（2）360°×=108°，‎ 答：“D”所在扇形的圆心角的度数为108°；‎ ‎（3）根据题意，16年补贴D类“插电式混合动力汽车”金额为：6+4.5×=7.35（千万元），‎ ‎∴7350÷3=2450（辆），‎ 答：预测该省16年计划大约共销售“插电式混合动力汽车”2450辆．‎ ‎　‎ ‎19．某大型企业为了保护环境，准备购买A、B两种型号的污水处理设备共8台，用于同时治理不同成分的污水，若购买A型2台、B型3台需54万，购买A型4台、B型2台需68万元．‎ ‎（1）求出A型、B型污水处理设备的单价；‎ ‎（2）经核实，一台A型设备一个月可处理污水220吨，一台B型设备一个月可处理污水190吨，如果该企业每月的污水处理量不低于1565吨，请你为该企业设计一种最省钱的购买方案．‎ ‎【考点】一元一次不等式的应用；二元一次方程组的应用．‎ ‎【分析】（1）根据题意结合购买A型2台、B型3台需54万，购买A型4台、B型2台需68万元分别得出等式求出答案；‎ ‎（2）利用该企业每月的污水处理量不低于1565吨，得出不等式求出答案．‎ ‎【解答】解：（1）设A型污水处理设备的单价为x万元，B型污水处理设备的单价为y万元，根据题意可得：‎ ‎，‎ 解得：．‎ 答：A型污水处理设备的单价为12万元，B型污水处理设备的单价为10万元；‎ ‎（2）设购进a台A型污水处理器，根据题意可得：‎ ‎220a+190（8﹣a）≥1565，‎ 解得：a≥1.5，‎ ‎∵A型污水处理设备单价比B型污水处理设备单价高，‎ ‎∴A型污水处理设备买越少，越省钱，‎ ‎∴购进2台A型污水处理设备，购进6台B型污水处理设备最省钱．‎ ‎　‎ ‎20．如图，在⊙O中，点C是直径AB延长线上一点，过点C作⊙O的切线，切点为D，连结BD．‎ ‎（1）求证：∠A=∠BDC；‎ ‎（2）若CM平分∠ACD，且分别交AD、BD于点M、N，当DM=1时，求MN的长．‎ ‎【考点】切线的性质．‎ ‎【分析】（1）由圆周角推论可得∠A+∠ABD=90°，由切线性质可得∠CDB+∠ODB=90°，而∠ABD=∠ODB，可得答案；‎ ‎（2）由角平分线及三角形外角性质可得∠A+∠ACM=∠BDC+∠DCM，即∠DMN=∠DNM，根据勾股定理可求得MN的长．‎ ‎【解答】解：（1）如图，连接OD，‎ ‎∵AB为⊙O的直径，‎ ‎∴∠ADB=90°，即∠A+∠ABD=90°，‎ 又∵CD与⊙O相切于点D，‎ ‎∴∠CDB+∠ODB=90°，‎ ‎∵OD=OB，‎ ‎∴∠ABD=∠ODB，‎ ‎∴∠A=∠BDC；‎ ‎（2）∵CM平分∠ACD，‎ ‎∴∠DCM=∠ACM，‎ 又∵∠A=∠BDC，‎ ‎∴∠A+∠ACM=∠BDC+∠DCM，即∠DMN=∠DNM，‎ ‎∵∠ADB=90°，DM=1，‎ ‎∴DN=DM=1，‎ ‎∴MN==．‎ ‎　‎ ‎21．如图，在平行四边形ABCD中，点A、B、C的坐标分别是（1，0）、（3，1）、（3，3），双曲线y=（k≠0，x＞0）过点D．‎ ‎（1）求双曲线的解析式；‎ ‎（2）作直线AC交y轴于点E，连结DE，求△CDE的面积．‎ ‎【考点】反比例函数与一次函数的交点问题；平行四边形的性质．‎ ‎【分析】（1）根据在平行四边形ABCD中，点A、B、C的坐标分别是（1，0）、（3，1）、（3，3），可以求得点D的坐标，又因为双曲线y=（k≠0，x＞0）过点D，从而可以求得k的值，从而可以求得双曲线的解析式；‎ ‎（2）由图可知三角形CDE的面积等于三角形EDA与三角形ADC的面积之和，从而可以解答本题．‎ ‎【解答】解：（1）∵在平行四边形ABCD中，点A、B、C的坐标分别是（1，0）、（3，1）、（3，3），‎ ‎∴点D的坐标是（1，2），‎ ‎∵双曲线y=（k≠0，x＞0）过点D，‎ ‎∴2=，得k=2，‎ 即双曲线的解析式是：y=；‎ ‎（2）∵直线AC交y轴于点E，‎ ‎∴S△CDE=S△EDA+S△ADC=，‎ 即△CDE的面积是3．‎ ‎　‎ ‎22．如图，“中国海监50”正在南海海域A处巡逻，岛礁B上的中国海军发现点A在点B的正西方向上，岛礁C上的中国海军发现点A在点C的南偏东30°方向上，已知点C在点B的北偏西60°方向上，且B、C两地相距120海里．‎ ‎（1）求出此时点A到岛礁C的距离；‎ ‎（2）若“中海监50”从A处沿AC方向向岛礁C驶去，当到达点A′时，测得点B在A′的南偏东75°的方向上，求此时“中国海监50”的航行距离．（注：结果保留根号）‎ ‎【考点】解直角三角形的应用-方向角问题．‎ ‎【分析】（1）根据题意得出：∠CBD=30°，BC=120海里，再利用cos30°=，进而求出答案；‎ ‎（2）根据题意结合已知得出当点B在A′的南偏东75°的方向上，则A′B平分∠CBA，进而得出等式求出答案．‎ ‎【解答】解：（1）如图所示：延长BA，过点C作CD⊥BA延长线与点D，‎ 由题意可得：∠CBD=30°，BC=120海里，‎ 则DC=60海里，‎ 故cos30°===，‎ 解得：AC=40，‎ 答：点A到岛礁C的距离为40海里；‎ ‎（2）如图所示：过点A′作A′N⊥BC于点N，‎ 可得∠1=30°，∠BA′A=45°，A′N=A′E，‎ 则∠2=15°，即A′B平分∠CBA，‎ 设AA′=x，则A′E=x，‎ 故CA′=2A′N=2×x=x，‎ ‎∵x+x=40，‎ ‎∴解得：x=20（﹣1），‎ 答：此时“中国海监50”的航行距离为20（﹣1）海里．‎ ‎　‎ ‎23．在Rt△ABC中，∠C=90°，Rt△ABC绕点A顺时针旋转到Rt△ADE的位置，点E在斜边AB上，连结BD，过点D作DF⊥AC于点F．‎ ‎（1）如图1，若点F与点A重合，求证：AC=BC；‎ ‎（2）若∠DAF=∠DBA，‎ ‎①如图2，当点F在线段CA的延长线上时，判断线段AF与线段BE的数量关系，并说明理由；‎ ‎②当点F在线段CA上时，设BE=x，请用含x的代数式表示线段AF．‎ ‎【考点】几何变换综合题．‎ ‎【分析】（1）由旋转得到∠BAC=∠BAD，而DF⊥AC，从而得出∠ABC=45°，最后判断出△ABC是等腰直角三角形；‎ ‎（2）①由旋转得到∠BAC=∠BAD，再根据∠DAF=∠DBA，从而求出∠FAD=∠BAC=∠BAD=60°，最后判定△AFD≌△BED，即可；‎ ‎②根据题意画出图形，先求出角度，得到△ABD是顶角为36°的等腰三角形，再用相似求出，，最后判断出△AFD∽△BED，代入即可．‎ ‎【解答】解：（1）由旋转得，∠BAC=∠BAD，‎ ‎∵DF⊥AC，‎ ‎∴∠CAD=90°，‎ ‎∴∠BAC=∠BAD=45°，‎ ‎∵∠ACB=90°，‎ ‎∴∠ABC=45°，‎ ‎∴AC=CB，‎ ‎（2）①由旋转得，AD=AB，‎ ‎∴∠ABD=∠ADB，‎ ‎∵∠DAF=∠ABD，‎ ‎∴∠DAF=∠ADB，‎ ‎∴AF∥BB，‎ ‎∴∠BAC=∠ABD，‎ ‎∵∠ABD=∠FAD 由旋转得，∠BAC=∠BAD，‎ ‎∴∠FAD=∠BAC=∠BAD=×180°=60°，‎ 由旋转得，AB=AD，‎ ‎∴△ABD是等边三角形，‎ ‎∴AD=BD，‎ 在△AFD和△BED中，‎ ‎，‎ ‎∴△AFD≌△BED，‎ ‎∴AF=BE，‎ ‎②如图，‎ 由旋转得，∠BAC=∠BAD，‎ ‎∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD，‎ 由旋转得，AD=AB，‎ ‎∴∠ABD=∠ADB=2∠BAD，‎ ‎∵∠BAD+∠ABD+∠ADB=180°，‎ ‎∴∠BAD+2∠BAD+2∠BAD=180°，‎ ‎∴∠BAD=36°，‎ 设BD=x，作BG平分∠ABD，‎ ‎∴∠BAD=∠GBD=36°‎ ‎∴AG=BG=BC=x，‎ ‎∴DG=AD﹣AG=AD﹣BG=AD﹣BD，‎ ‎∵∠BDG=∠ADB，‎ ‎∴△BDG∽△ADB，‎ ‎∴．‎ ‎∴，‎ ‎∴，‎ ‎∵∠FAD=∠EBD，∠AFD=∠BED，‎ ‎∴△AFD∽△BED，‎ ‎∴，‎ ‎∴AF==x．‎ ‎　‎ ‎24．已知抛物线与x轴交于A（6，0）、B（﹣，0）两点，与y轴交于点C，过抛物线上点M（1，3）作MN⊥x轴于点N，连接OM．‎ ‎（1）求此抛物线的解析式；‎ ‎（2）如图1，将△OMN沿x轴向右平移t个单位（0≤t≤5）到△O′M′N′的位置，MN′、M′O′与直线AC分别交于点E、F．‎ ‎①当点F为M′O′的中点时，求t的值；‎ ‎②如图2，若直线M′N′与抛物线相交于点G，过点G作GH∥M′O′交AC于点H，试确定线段EH是否存在最大值？若存在，求出它的最大值及此时t的值；若不存在，请说明理由．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）设抛物线解析式为y=a（x﹣6）（x+），把点M（1，3）代入即可求出a，进而解决问题．‎ ‎（2））①如图1中，AC与OM交于点G．连接EO′，首先证明△AOC∽△MNO，推出OM⊥AC，在RT△EO′M′中，利用勾股定理列出方程即可解决问题．‎ ‎②由△GHE∽△AOC得==，所以EG最大时，EH最大，构建二次函数求出EG的最大值即可解决问题．‎ ‎【解答】解：（1）设抛物线解析式为y=a（x﹣6）（x+），把点M（1，3）代入得a=﹣，‎ ‎∴抛物线解析式为y=﹣（x﹣6）（x+），‎ ‎∴y=﹣x2+x+2．‎ ‎（2）①如图1中，AC与OM交于点G．连接EO′．‎ ‎∵AO=6，OC=2，MN=3，ON=1，‎ ‎∴==3，‎ ‎∴=，∵∠AOC=∠MON=90°，‎ ‎∴△AOC∽△MNO，‎ ‎∴∠OAC=∠NMO，‎ ‎∵∠NMO+∠MON=90°，‎ ‎∴∠MON+∠OAC=90°，‎ ‎∴∠AGO=90°，‎ ‎∴OM⊥AC，‎ ‎∵△M′N′O′是由△MNO平移所得，‎ ‎∴O′M′∥OM，‎ ‎∴O′M′⊥AC，‎ ‎∵M′F=FO′，‎ ‎∴EM′=EO′，‎ ‎∵EN′∥CO，‎ ‎∴=，‎ ‎∴=，‎ ‎∴EN′=（5﹣t），‎ 在RT△EO′M′中，∵O′N′=1，EN′=（5﹣t），EO′=EM′=+t，‎ ‎∴（+t）2=1+（﹣t）2，‎ ‎∴t=1．‎ ‎②如图2中，‎ ‎∵GH∥O′M′，O′M′⊥AC，‎ ‎∴GH⊥AC，‎ ‎∴∠GHE=90°，‎ ‎∵∠EGH+∠HEG=90°，∠AEN′+∠OAC=90°，∠HEG=∠AEN′，‎ ‎∴∠OAC=∠HGE，∵∠GHE=∠AOC=90°，‎ ‎∴△GHE∽△AOC，‎ ‎∴==，‎ ‎∴EG最大时，EH最大，‎ ‎∵EG=GN′﹣EN′=﹣（t+1）2+（t+1）+2﹣（5﹣t）=﹣t2+t+=﹣（t﹣2）2+．‎ ‎∴t=2时，EG最大值=，‎ ‎∴EH最大值=．‎ ‎∴t=2时，EH最大值为．‎ ‎　‎ ‎2016年7月1日