2009年山东省淄博市中等学校招生考试试题及答案 17页

绝密★启用前 试卷类型：A ‎ 淄博市二○○九年中等学校招生考试 数 学 试 题 注意事项：‎ ‎1．答题前请考生务必在答题卡及试卷的规定位置将自己的姓名、考试号、考试科目、座号等内容填写（涂）准确． ‎ ‎2．本试题分第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷（1—4页）为选择题，36分；第Ⅱ卷（5—12页）为非选择题，84分；共120分．考试时间为120分钟．‎ ‎3．第Ⅰ卷每小题选出答案后，必须用2B铅笔把答题卡上对应题目的答案标号（ABCD）涂黑．如需改动，须先用橡皮擦干净，再改涂其它答案．第Ⅱ卷须用蓝黑钢笔或圆珠笔直接答在试卷上．考试时，不允许使用计算器．‎ ‎4．考试结束后，由监考教师把第Ⅰ卷和第Ⅱ卷及答题卡一并收回． ‎ 第Ⅰ卷（选择题 共36分）‎ 一、选择题：本题共12小题，在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项涂在答题卡的相应位置上．每小题3分，错选、不选或选出的答案超过一个，均记0分．‎ ‎1．如果，则“”内应填的实数是 ‎(A) (B) (C) (D)‎ ‎2．计算的结果是 ‎(A) (B) (C) (D)‎ ‎3．在等腰直角三角形ABC中，∠C=90º，则sinA等于 ‎(A) (B)‎ ‎(C) (D)1 ‎ ‎4．化简的结果为 ‎(A) (B) ‎ ‎(C) (D)‎ ‎5．小明在白纸上任意画了一个锐角，他画的角在45º到60º之间的概率是 ‎(A) (B) ‎ ‎(C) (D)‎ ‎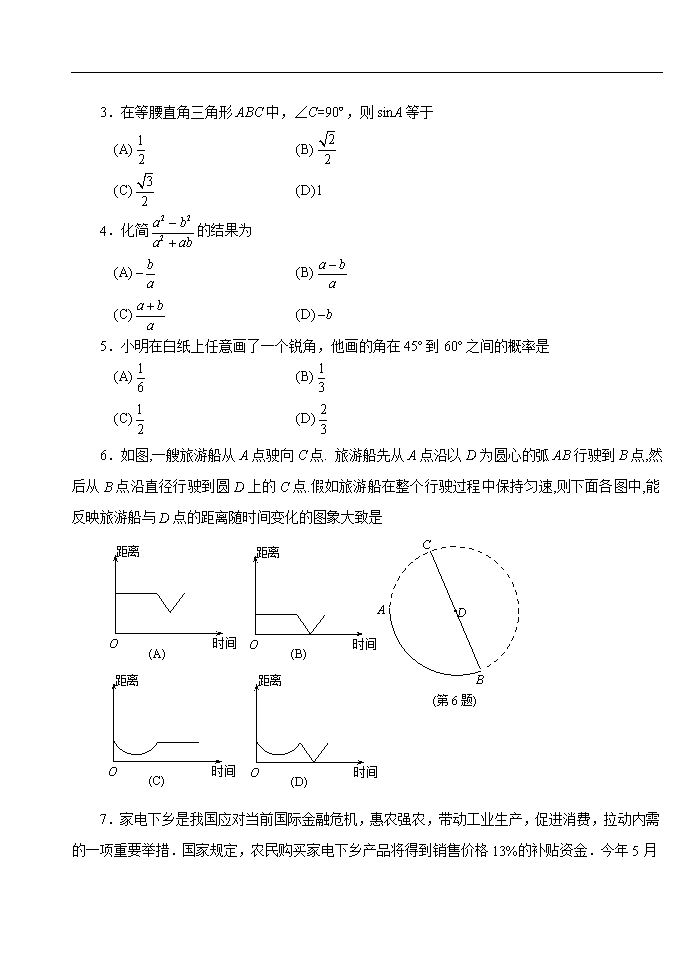6．如图,一艘旅游船从A点驶向C点. 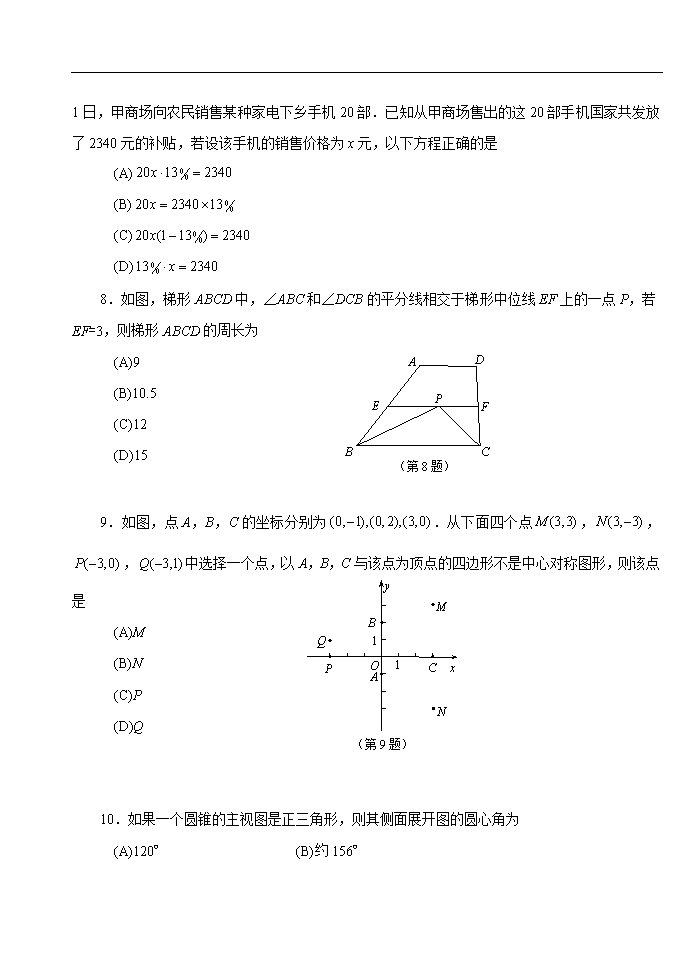旅游船先从A点沿以D为圆心的弧AB行驶到B点,然后从B点沿直径行驶到圆D上的C点.假如旅游船在整个行驶过程中保持匀速,则下面各图中,能反映旅游船与D点的距离随时间变化的图象大致是 A B D ‎(第6题)‎ C 时间 距离 O ‎(B)‎ 时间 距离 O ‎(A)‎ 时间 距离 O ‎(C)‎ 时间 距离 O ‎(D)‎ ‎7．家电下乡是我国应对当前国际金融危机，惠农强农，带动工业生产，促进消费，拉动内需的一项重要举措．国家规定，农民购买家电下乡产品将得到销售价格13%的补贴资金．今年5月 ‎1日，甲商场向农民销售某种家电下乡手机20部．已知从甲商场售出的这20部手机国家共发放了2340元的补贴，若设该手机的销售价格为x元，以下方程正确的是 ‎(A) ‎ ‎(B)‎ ‎(C) ‎ ‎(D)‎ ‎8．如图，梯形ABCD中，∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P，若EF=3，则梯形ABCD的周长为 A B C D E F P ‎（第8题）‎ ‎(A)9 ‎ ‎(B)10.5‎ ‎(C)12 ‎ ‎(D)15‎ y A C O x B M N P Q ‎（第9题）‎ ‎1‎ ‎1‎ ‎9．如图，点A，B，C的坐标分别为．从下面四个点，，，中选择一个点，以A，B，C与该点为顶点的四边形不是中心对称图形，则该点是 ‎(A)M ‎ ‎(B)N ‎ ‎(C)P ‎ ‎(D)Q ‎10．如果一个圆锥的主视图是正三角形，则其侧面展开图的圆心角为 ‎(A)120º (B)约156º ‎ ‎(C)180º (D)约208º A B C D E G F ‎（第11题）‎ F ‎11．矩形纸片ABCD的边长AB=4，AD=2．将矩形纸片沿EF折叠，使点A与点C重合，折叠后在其一面着色(如图)，则着色部分的面积为 ‎(A) 8 ‎ ‎(B) ‎ ‎(C) 4 ‎ ‎(D)‎ x y O A(-2，-1)‎ B(-3，0)‎ ‎(第12题)‎ ‎12．如图，直线经过和两点，利用函数图象判断不等式的解集为 ‎(A) ‎ ‎(B) ‎ ‎(C)‎ ‎(D)‎ ‎（第6题）‎ 绝密★启用前 试卷类型：A 淄博市二○○九年中等学校招生考试 数 学 试 题 第Ⅱ卷（非选择题 共84分）‎ 得 分 评 卷 人 ‎ ‎ 二、填空题：本题共5小题，满分20分．只要求填写最后结果，每小题填对得4分．‎ ‎13．国家统计局2009年4月16日发布:一季度，农村居民人均现金收入1622元，与去年同期相比增长8.6%，将1622元用科学记数法表示 为 元． ‎ ‎14．时代中学举行了一次科普知识竞赛.满分100分,学生得分的最低分31分．如图是根据学生竞赛成绩绘制的频数分布直方图的一部分．参加这次知识竞赛的学生共有40人，则得分在60~70分的频率为 ． ‎ 成绩/分 人数/人 ‎30‎ ‎40‎ ‎50‎ ‎60‎ ‎70‎ ‎80‎ ‎90‎ ‎100‎ ‎5‎ ‎10‎ ‎15‎ ‎(第14题)‎ ‎0‎ ‎ ‎ A Ｂ Ｃ Ｄ E F ‎（第15题）‎ G H ‎15．如图，四边形EFGH是由四边形经过旋转得到的．如果用有序数对(2,1)表示方格纸上A点的位置，用(1,2)表示B点的位置，那么四边形旋转得到四边形EFGH时的旋转中心用有序数对表示是　　 　．‎ C ‎16．请写出符合以下三个条件的一个函数的解析式 ．‎ ‎①过点；‎ ‎②在第一象限内y随x的增大而减小；‎ ‎③当自变量的值为2时，函数值小于2．‎ ‎17．如图，网格中的每个四边形都是菱形．如果格点三角形ABC的面积为S，按照如图所示方式得到的格点三角形A1B1C1的面积是，格点三角形A2B2C2的面积是19S，那么格点三角形A3B3C3的面积为 ．‎ A A1‎ A2‎ A3‎ B3‎ B2‎ B1‎ B C1‎ C2‎ C3‎ ‎（第17题）‎ C ‎ ‎ 三、解答题：本大题共8小题，共64分．解答要写出必要的文字说明、证明过程或演算步骤．‎ 得 分 评 卷 人 ‎18．(本题满分6分)‎ 解不等式：5x–12≤2(4x-3)‎ 得 分 评 卷 人 ‎19．(本题满分6分)‎ A B C D E ‎（第19题）‎ 如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A=37º，求∠D的度数．‎ 得 分 评 卷 人 ‎20． (本题满分8分)‎ 如图，在3×3的方阵图中，填写了一些数和代数式(其中每个代数式都表示一个数)，使得每行的３个数、每列的３个数、斜对角的３个数之和均相等．‎ ‎–2‎ ‎3‎ ‎4‎ ‎(备用图)‎ ‎2y–x ‎–2‎ ‎3‎ ‎4‎ x y ‎(第20题)‎ a b c ‎(1)求x，y的值；‎ ‎(2)在备用图中完成此方阵图．‎ 得 分 评 卷 人 ‎21． (本题满分8分)‎ 某中学共有学生2000名，各年级男女生人数如下表：‎ 六年级 七年级 八年级 九年级 男生 ‎250‎ z ‎254‎ ‎258‎ 女生 x ‎244‎ y ‎252‎ 若从全校学生中任意抽一名，抽到六年级女生的概率是0.12；若将各年级的男、女生人数制作成扇形统计图，八年级女生对应扇形的圆心角为44.28°．‎ ‎（1）求x，y，z的值；‎ ‎（2）求各年级男生的中位数；‎ ‎（3）求各年级女生的平均数；‎ ‎（4）从八年级随机抽取36名学生参加社会实践活动，求抽到八年级某同学的概率．‎ 得 分 评 卷 人 ‎ 22． (本题满分8分)‎ 如图，两个同心圆的圆心是O，大圆的半径为13，小圆的半径为5，AD是大圆的直径．大圆的弦AB，BE分别与小圆相切于点C，F．AD，BE相交于点G，连接BD．‎ A C B D G F E O ‎(第22题)‎ ‎(1)求BD 的长；‎ ‎(2)求∠ABE+2∠D的度数；‎ ‎(3)求的值．‎ 得 分 评 卷 人 ‎23． (本题满分8分)‎ 题号 得分 二 三 ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ 总分 已知是方程的两个实数根，且．‎ ‎(1)求及a的值；‎ ‎(2)求的值．‎ 座号 得 分 评 卷 人 ‎24． (本题满分10分)‎ 如图，在平面直角坐标系中，正方形OABC的边长是2．O为坐标原点，点A在x的正半轴上，点C在y的正半轴上．一条抛物线经过A点，顶点D是OC的中点．‎ ‎（1）求抛物线的表达式；‎ ‎（2）正方形OABC的对角线OB与抛物线交于E点，线段FG过点E与x轴垂直，分别交x轴和线段BC于F，G点，试比较线段OE与EG的长度；‎ O A B C D E y x F G H I J K ‎（第24题）‎ ‎（3）点H是抛物线上在正方形内部的任意一点，线段IJ过点H与x轴垂直，分别交x轴和线段BC于I、J点，点K在y轴的正半轴上，且OK=OH，请证明△OHI≌△JKC．‎ 得 分 评 卷 人 ‎25． (本题满分10分)‎ 如图，在矩形ABCD中，BC=20cm，P，Q，M，N分别从A，B，C，D出发沿AD，BC，CB，DA方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停止．已知在相同时间内，若BQ=xcm()，则AP=2xcm，CM=3xcm，DN=x2cm．‎ ‎（1）当x为何值时，以PQ，MN为两边,以矩形的边（AD或BC）的一部分为第三边构成一个三角形；‎ ‎（2）当x 为何值时，以P，Q，M，N为顶点的四边形是平行四边形；‎ ‎（3）以P，Q，M，N为顶点的四边形能否为等腰梯形?如果能，求x的值；如果不能，请说明理由．‎ A B D C P Q M N ‎（第25题）‎ 淄博市二○○九年中等学校招生考试 数学试题（A卷）参考答案及评分标准 评卷说明：‎ ‎1．选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分．‎ ‎2．解答题每小题的解答中所对应的分数，是指考生正确解答到该步骤所应得的累计分数．每小题只给出一种或两种解法，对考生的其它解法，请参照评分意见进行评分．‎ ‎3．如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分就不再给分．‎ 一、选择题（本大题共12小题，每小题3分，共36分）：‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D D B B A B A C C C B D 二、填空题 （本大题共5小题，每小题4分，共20分） ：‎ ‎13． 14．0．1 15．（5，2） ‎ ‎16．如 　　 17．37S 三、解答题 （本大题共8小题，共64分） ：‎ ‎18．（本题满分6分）‎ 解：5x–12≤8x-6． 2分 ‎≤6． 4分 x≥-2 ． 6分 ‎19．（本题满分6分） ‎ 解： ∵AB∥CD， ∠A=37º，‎ ‎∴∠ECD=∠A=37º． 3分 ‎∵DE⊥AE，‎ ‎∴∠D=90º–∠ECD=90º–37º=53º． 6分 ‎20．（本题满分8分）‎ ‎–2‎ ‎3‎ ‎4‎ ‎–1‎ ‎6‎ ‎1‎ ‎0‎ ‎5‎ ‎2‎ 解：（1）由题意，得 2分 解得 5分 ‎（2）如图 8分 ‎21．（本题满分8分） ‎ 解： （1）由题意：‎ ‎（人）． 1分 ‎（人）． 2分 z=2000－250－240－244－254－246－258－252=256（人）． 3分 ‎（2）各年级男生的中位数为（人）． 4分 ‎（3）各年级女生的平均数为（人）． 6分 ‎（4）抽到八年级某同学的概率为． 8分 A C B D G F E O ‎（第22题）‎ H ‎22．（本题满分8分）‎ 解： （1）连接OC，并延长BO交AE于点H，‎ ‎∵AB是小圆的切线，C是切点，‎ ‎∴OC⊥AB，‎ ‎∴C是AB的中点． 1分 ‎∵AD是大圆的直径，‎ ‎∴O是AD的中点．‎ ‎∴OC是△ABD的中位线．‎ ‎∴BD=2OC=10． 2分 ‎（2） 连接AE，由（1）知C是AB的中点．‎ 同理F是BE的中点．‎ 由切线长定理得BC=BF．‎ ‎∴BA=BE． 3分 ‎∴∠BAE=∠E．‎ ‎∵∠E=∠D， 4分 ‎∴∠ABE+2∠D=∠ABE+∠E+∠BAE=180º． 5分 ‎（3） 连接BO，在Rt△OCB中，‎ ‎∵OB=13，OC=5，‎ ‎∴BC=12． 6分 由（2）知∠OBG=∠OBC=∠OAC．‎ ‎∵∠BGO=∠AGB，‎ ‎∴△BGO∽△AGB． 7分 ‎∴． 8分 ‎23．（本题满分8分）‎ 解：（1）由题意，得 2分 解得． 3分 所以． 4分 ‎（2）法一： 由题意，得．‎ 所以= 6分 ‎=． 8分 法二： 由题意，得，‎ 所以= 6分 ‎== ‎ ‎=． 8分 ‎24．（本题满分10分）‎ 解：（1）由题意，设抛物线的解析式为：． 1分 将点D的坐标（0，1），点A的坐标（2，0）代入，得 a = ，b=1．‎ 所求抛物线的解析式为． 3分 ‎（2）由于点E在正方形的对角线OB上，又在抛物线上，‎ 设点E的坐标为（m，m）（），则． ‎ 解得 （舍去）． 4分 所以OE=． 5分 所以．‎ 所以OE=EG． 6分 ‎（3）设点H的坐标为（p，q）（，），‎ 由于点H在抛物线上，‎ 所以，即．‎ 因为， 8分 所以OH=2–q．‎ 所以OK=OH=2–q．‎ 所以CK=2－（2－q）=q=IH． 9分 因为CJ=OI， ∠OIH=∠JCK=90º，‎ 所以△OHI≌△JKC． 10分 ‎25．（本题满分10分）‎ 解：（1）当点P与点N重合或点Q与点M重合时，以PQ，MN为两边，以矩形的边（AD或BC）的一部分为第三边可能构成一个三角形．‎ ‎①当点P与点N重合时，‎ ‎（舍去）． 1分 因为BQ+CM=，此时点Q与点M不重合．‎ 所以符合题意． 2分 ‎②当点Q与点M重合时，‎ ‎．‎ 此时，不符合题意．‎ 故点Q与点M不能重合．‎ 所以所求x的值为． 3分 ‎（2）由（1）知，点Q 只能在点M的左侧，‎ ‎①当点P在点N的左侧时，‎ 由，‎ 解得．‎ 当x=2时四边形PQMN是平行四边形． 5分 ‎②当点P在点N的右侧时，‎ 由， ‎ 解得．‎ 当x=4时四边形NQMP是平行四边形．‎ 所以当时，以P，Q，M，N为顶点的四边形是平行四边形． 7分 ‎（3）过点Q，M分别作AD的垂线，垂足分别为点E，F．‎ 由于2x>x，‎ 所以点E一定在点P的左侧．‎ 若以P，Q，M，N为顶点的四边形是等腰梯形， ‎ 则点F一定在点N的右侧，且PE=NF， 8分 即．‎ 解得．‎ 由于当x=4时， 以P，Q，M，N为顶点的四边形是平行四边形，‎ 所以以P，Q，M，N为顶点的四边形不能为等腰梯形． 10分