2009年黑龙江省大兴安岭地区初中毕业学业考试及答案 13页

二○○九年大兴安岭地区初中毕业学业考试 数 学 试 卷 本考场试卷序号 ‎（由监考填写）‎ 考生注意： ‎1．考试时间120分钟 ‎2．全卷共三道大题，总分120分 题 号 一 二 三 总 分 核分人 ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ ‎26‎ ‎27‎ ‎28‎ 得 分 得 分 评卷人 一、填空题（每题3分，满分33分）‎ ‎1．的绝对值是 ． ‎ ‎2．函数中，自变量的取值范围是 ．‎ 第5题图 ‎3．联合国环境规划署发布报告称：2008年尽管全球投资市场普遍疲软，但在中国等发展中国家的带动下，全球可持续投资再创历史新高，达1550亿美元．这个数用科学记数法可表示为 美元． ‎ ‎4．计算： ．‎ ‎5．反比例函数的图象如图所示，请写出一条 正确的结论： ． ‎ ‎6．已知相切两圆的半径分别为和，这两个圆的圆心距是 ．‎ 第8题图 A B C D ‎7．在英语句子“Wish you success！”（祝你成功！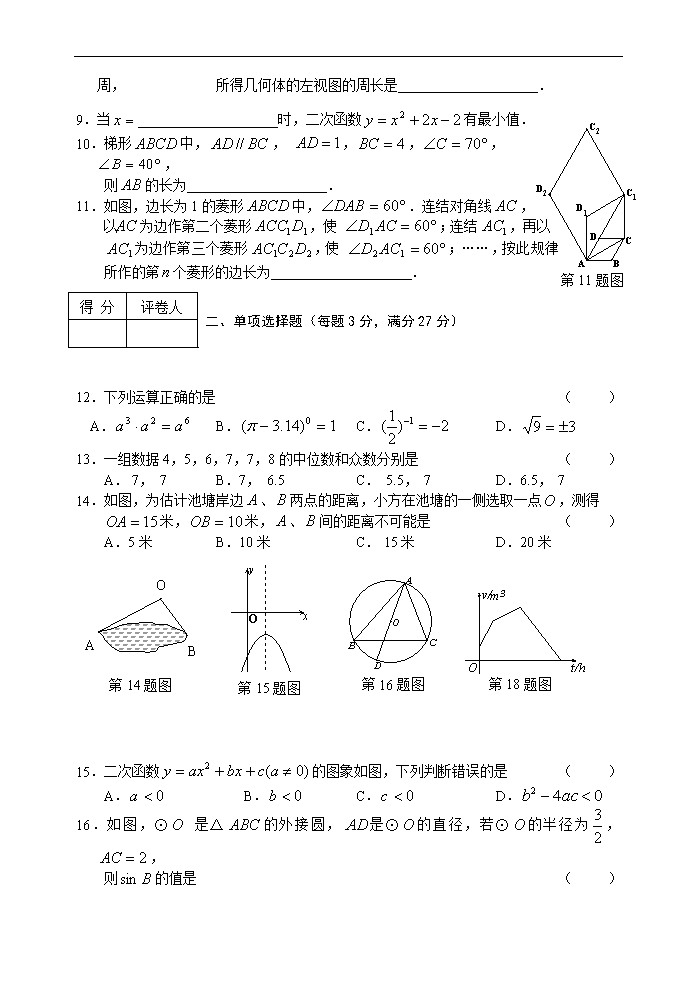）中任选一个字母，这个字母为“s”的概率是 ．‎ ‎8．如图，正方形的边长为3，以直线 为轴，将正方形旋转一周， 所得几何体的左视图的周长是 ． ‎ 第11题图 ‎9．当 时，二次函数有最小值． ‎ ‎10．梯形中，， ，，，， ‎ 则的长为 ． ‎ ‎11．如图，边长为1的菱形中，．连结对角线，以为边作第二个菱形，使 ；连结，再以为边作第三个菱形，使 ；……，按此规律所作的第个菱形的边长为 ．‎ 得 分 评卷人 二、单项选择题（每题3分，满分27分）‎ ‎12．下列运算正确的是 （ ）‎ A． B． C． D． ‎ ‎13．一组数据4，5，6，7，7，8的中位数和众数分别是 （ ）‎ A． 7， 7 B．7， ‎6.5 ‎ C． 5.5， 7 D．6.5， 7‎ ‎14．如图，为估计池塘岸边、两点的距离，小方在池塘的一侧选取一点，测得米，米，、间的距离不可能是 （ ）‎ A．‎5米 B．‎10米 C． ‎15米 D．‎‎20米 第15题图 O B A 第14题图 第16题图 第18题图 ‎15．二次函数的图象如图，下列判断错误的是 （ ）‎ A． B． C． D．‎ ‎16．如图，⊙ 是△的外接圆，是⊙的直径，若⊙的半径为，， ‎ 则的值是 （ ）‎ A． B． C． D． ‎ ‎17．用两个全等的直角三角形拼成凸四边形，拼法共有 （ ）‎ A．3种 B．4种 C．5种 D．6种 ‎18．一个水池接有甲、乙、丙三个水管，先打开甲，一段时间后再打开乙，水池注满水后关闭甲，同时打开丙，直到水池中的水排空．水池中的水量与时间之间的函数关系如图，则关于三个水管每小时的水流量，下列判断正确的是 （ ）‎ A．乙>甲 B． 丙>甲 C．甲>乙 D．丙>乙 ‎ ‎19．一宾馆有二人间、三人间、四人间三种客房供游客租住，某旅行团20人准备同时租用这三种客房共7间，如果每个房间都住满，租房方案有 （ ）‎ A． 4种 B．3种 C．2种 D．1种 第20题图 ‎20．在矩形中，，，平分，过点作于，延长、交于点，下列结论中：①；②；③；④，正确的 （ ）‎ A．②③ B．③④ ‎ C．①②④ D．②③④ ‎ 三、解答题（本题满分60分）‎ 得 分 评卷人 ‎21．（本小题满分5分）‎ 先化简：，当时，请你为任选一个适当的数代入求值．‎ 得 分 评卷人 ‎22．（本小题满分6分）‎ 如图，在平面直角坐标系中，的顶点坐标为、、．‎ ‎（1）若将向右平移3个单位长度，再向上平移1个单位长度，请画出平移后的；‎ ‎（2）画出绕原点旋转后得到的；‎ ‎（3）与是位似图形，请写出位似中心的坐标： ；‎ ‎（4）顺次连结、、、，所得到的图形是轴对称图形吗？‎ 得 分 评卷人 ‎23．（本小题满分6分）‎ 在边长为4和6的矩形中作等腰三角形，使等腰三角形的一条边是矩形的长或宽，第三个顶点在矩形的边上，求所作三角形的面积．‎ ‎（注：形状相同的三角形按一种计算．）‎ 得 分 评卷人 ‎24．（本小题满分7分）‎ 为了解某地区30万电视观众对新闻、动画、娱乐三类节目的喜爱情况，根据老年人、成年人、青少年各年龄段实际人口的比例3︰5︰2，随机抽取一定数量的观众进行调查，得到如下统计图．‎ 图二：成年人喜爱的节目统计图 图一：观众喜爱的节目统计图 A B ‎（1）上面所用的调查方法是 （填“全面调查”或“抽样调查”）；‎ ‎（2）写出折线统计图中A、B所代表的值；‎ ‎ A： ；B： ；‎ ‎（3）求该地区喜爱娱乐类节目的成年人的人数．‎ 得 分 评卷人 ‎25．（本小题满分8分）‎ 邮递员小王从县城出发，骑自行车到A村投递，途中遇到县城中学的学生李明从A村步行返校．小王在A村完成投递工作后，返回县城途中又遇到李明，便用自行车载上李明，一起到达县城，结果小王比预计时间晚到1分钟．二人与县城间的距离(千米)和小王从县城出发后所用的时间(分)之间的函数关系如图，假设二人之间交流的时间忽略不计，求：‎ ‎（1）小王和李明第一次相遇时，距县城多少千米？请直接写出答案．‎ ‎（2）小王从县城出发到返回县城所用的时间．‎ ‎（3）李明从A村到县城共用多长时间？‎ 得 分 评卷人 ‎26．（本小题满分8分）‎ 已知：在中，，动点绕的顶点逆时针旋转，且，连结．过、的中点、作直线，直线与直线、分别相交于点 ‎、．‎ 图2‎ 图3‎ 图1‎ ‎(N)‎ ‎（1）如图1，当点旋转到的延长线上时，点恰好与点重合，取的中点，连结、，根据三角形中位线定理和平行线的性质，可得结论（不需证明）．‎ ‎（2）当点旋转到图2或图3中的位置时，与有何数量关系？请分别写出猜想，并任选一种情况证明．‎ 得 分 评卷人 ‎27．（本小题满分10分）‎ 某电脑公司经销甲种型号电脑，受经济危机影响，电脑价格不断下降．今年三月份的电脑售价比去年同期每台降价1000元，如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元．‎ ‎（1）今年三月份甲种电脑每台售价多少元？‎ ‎（2）为了增加收入，电脑公司决定再经销乙种型号电脑．已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台，有几种进货方案？‎ ‎（3）如果乙种电脑每台售价为3800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金元，要使（2）中所有方案获利相同，值应是多少？此时，哪种方案对公司更有利？‎ 得 分 评卷人 ‎28．（本小题满分10分）‎ 直线与坐标轴分别交于、两点，、的长分别是方程的两根（），动点从点出发，沿路线→→以每秒1个单位长度的速度运动，到达点时运动停止． ‎ ‎（1）直接写出、两点的坐标；‎ ‎（2）设点的运动时间为(秒)，的面积为，求与之间的函数关系式（不必写出自变量的取值范围）；‎ ‎（3）当时，直接写出点的坐标，此时，在坐标轴上是否存在点，使以、、、为顶点的四边形是梯形？若存在，请直接写出点的坐标；若不存在，请说明理由．‎ ‎ ‎ ‎2009年大兴安岭地区初中毕业学业考试 数学试卷参考答案及评分标准 一、填空题（多答案题全部答对得3分，否则不得分，带单位的答案，不写单位扣1分）‎ ‎1. 2. 且 3. ‎ ‎4. 5. 正确即可 6.或 ‎7. 8. 18 9. -1‎ ‎10. 3 11.‎ 二、选择题 ‎12. B 13. D 14. A ‎15. B 16. A 17. B ‎ ‎18. C 19. C 20. D 三、解答题 ‎21. 原式分 ‎ 分 ‎ 分 ‎ 值正确（、）给1分, 计算结果正确 给1分.‎ ‎22. 画出平移后的图形……………2分,‎ ‎ 画出旋转后的图形…………….2分,‎ ‎ 写出坐标(0, 0)………………….1分,‎ ‎ 答出“是轴对称图形”………..1分.‎ ‎23. .........................各1分, 面积是12………………1分 ‎………………..各1分, 面积是8和12………………1分 ‎24. 抽样调查………………..1分， ‎ ‎ A=20, B=40…………………….. 各1分,‎ ‎……………………..1分, ‎ ‎……………………1分, ‎ ‎………………2分 ‎ 25. (1) ‎4千米…………………..2分,‎ ‎ (2)解法一: ……………..1分 ‎ ……………..1分 ‎ 84+1=85……………………..1分 ‎ 解法二: 求出解析式……………………..1分,‎ ‎ ……………………..1分 ‎ 84+1=85……………………..1分 ‎ (3) 写出解析式…………………1分 ‎ …………………1分 ‎ 20+85=105………………………..1分 ‎26. 图2：…………………………2分 ‎ 图3：…………………………2分 证明：如图2，取的中点，连结、…………1分 ‎∵是的中点，是的中点，‎ ‎∴，， ‎ ‎∴．………………….1分 同理，，，‎ ‎∴．…………………………. 1分 ‎∵，‎ ‎∴, ‎ ‎∴‎ 图3‎ ‎∴．………………… 1分 ‎ ‎ 证明图3的过程与证明图2过程给分相同. ‎ ‎27. 解：(1)设今年三月份甲种电脑每台售价元 ‎………………………………1分 解得: ………………………………..1分 经检验: 是原方程的根, ……………………….1分 所以甲种电脑今年三月份每台售价4000元. ‎ ‎(2)设购进甲种电脑台,‎ ‎ ……………………….2分 解得 ………………………………………………………1分 因为的正整数解为6,7,8,9,10, 所以共有5种进货方案……………..1分 ‎(3) 设总获利为元, ‎ ‎…………1分 ‎ 当时, (2)中所有方案获利相同. ……………………………….1分 ‎ 此时, 购买甲种电脑6台,乙种电脑9台时对公司更有利. …………..1分 ‎28. (1) ……………………….各1分 ‎ (2)∵，，∴‎ ‎ 当点 在上运动时，，‎ ‎；..............1分 当点 在上运动时，作于点，‎ 有 ‎∵，∴………………………1分 ‎∴……………………1分 ‎（3）当时，，，………………………………1分 ‎ 此时，过各顶点作对边的平行线，与坐标轴无第二个交点，所以点不存在；……………………………………………………………………………1分 ‎ 当时，，，……………………1分 ‎ 此时，、………………………………………各1分 注: 本卷中各题, 若有其它正确的解法,可酌情给分.‎