2010年柳州市初中毕业升学考试试卷数学含答案 12页

‎2010年柳州市初中毕业升学考试试卷 数学 ‎（考试时间共120分钟，全卷满分120分）‎ 第Ⅰ卷（选择题，共36分）‎ 注意事项：‎ ‎1．答题前，考生务必先将自己的姓名、准考证号用蓝、黑色墨水笔或圆珠笔填写在试卷左边的密封线内．‎ ‎2．第Ⅰ卷为第1页至第2页．答题时，请用2B铅笔把各小题正确答案序号填涂在答题卡对应的题号内．如需改动，须用橡皮擦干净后，再填涂其它答案．‎ 在第Ⅰ卷上答题无效．‎ 一、选择题（本大题共12小题，每小题3分，满分36分．在每个小题给出的四个选项中，只有一项是正确的，每小题选对得3分，错选、不选或多选均得零分）‎ ‎1．的相反数是 图1‎ A．　　　　　Ｂ．　　　　　Ｃ．　　　　　Ｄ．‎ ‎2．如图1，点是直线上的三个点，图中共有线段条数是 A．1条　　　Ｂ．2条　　　Ｃ．3条　　　Ｄ．4条 ‎3．三条直线，若，，则与的位置关系是 A．　　　　Ｂ．　　　　Ｃ．　　　　Ｄ．无法确定 ‎4．图2的几何体中，主视图、左视图、俯视图均相同的是 图2‎ ‎5．若分式有意义，则的取值范围是 A．　　　Ｂ．　　　Ｃ．　　　Ｄ．‎ ‎6．不等式的解集在数轴上表示为 A．　　　　　　　　B.　　　　　　　　　　C.　　　　　　　　　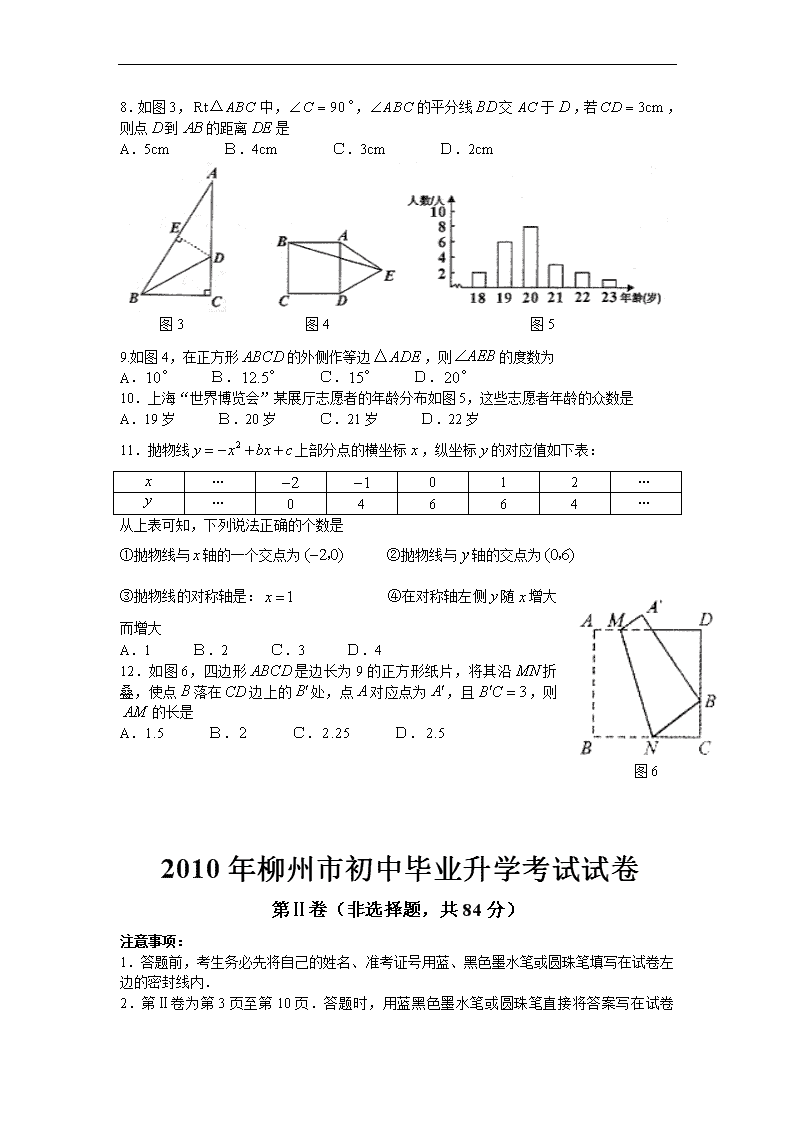D.‎ ‎7．一个正多边形的一个内角为120度，则这个正多边形的边数为 A．9　　　Ｂ．8　　　Ｃ．7　　　Ｄ．6‎ ‎8．如图3，中，，的平分线交于，若，则点到的距离是 A．‎5cm　　　　Ｂ．‎4cm　　　　Ｃ．‎3cm　　　　Ｄ．‎‎2cm 图3‎ 图4‎ 图5‎ ‎9.如图4，在正方形的外侧作等边，则的度数为 A．　　　Ｂ．　　　Ｃ．　　　Ｄ．‎ ‎10．上海“世界博览会”某展厅志愿者的年龄分布如图5，这些志愿者年龄的众数是 A．19岁　　　Ｂ．20岁　　　Ｃ．21岁　　　Ｄ．22岁 ‎11．抛物线上部分点的横坐标，纵坐标的对应值如下表：‎ ‎…‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ ‎…‎ ‎0‎ ‎4‎ ‎6‎ ‎6‎ ‎4‎ ‎…‎ 从上表可知，下列说法正确的个数是 ‎①抛物线与轴的一个交点为　　　②抛物线与轴的交点为 图6‎ ‎③抛物线的对称轴是：　　　　　　 ④在对称轴左侧随增大而增大 A．1　　　Ｂ．2　　　Ｃ．3　　　Ｄ．4‎ ‎12．如图6，四边形是边长为9的正方形纸片，将其沿折叠，使点落在边上的处，点对应点为，且，则的长是 A．　　　Ｂ．　　　Ｃ．　　　Ｄ．‎ ‎2010年柳州市初中毕业升学考试试卷 第Ⅱ卷（非选择题，共84分）‎ 注意事项：‎ ‎1．答题前，考生务必先将自己的姓名、准考证号用蓝、黑色墨水笔或圆珠笔填写在试卷左边的密封线内．‎ ‎2．第Ⅱ 卷为第3页至第10页．答题时，用蓝黑色墨水笔或圆珠笔直接将答案写在试卷上．‎ 二、填空题（本大题共6小题，每小题3分，满分18分．请将答案直接填写在题中横线上的空白处）‎ ‎13．计算：=　　　　．‎ ‎14．因式分解：　　　　．‎ ‎15．写出一个经过点的一次函数解析式　　　　．‎ 图7‎ ‎16．2010年广州亚运会吉祥物取名“乐羊羊”．图7中各图是按照一定规律排列的羊的组图，图有1只羊，图有3只羊，……，则图⑩有　　　　只羊．‎ 图8‎ ‎17．关于的一元二次方程的根是　　　　．‎ ‎18．如图8，是的直径，弦，是弦的中点，．若动点以的速度从点出发沿着方向运动，设运动时间为，连结，当值为　　　　时，是直角三角形．‎ 三、解答题（本大题8分，满分66分．解答应写出必要的文字说明、演算步骤或推理过程）‎ ‎19．（本题满分6分）‎ 计算：．‎ ‎20．（本题满分6分）‎ 如图9，在的正方形网格中，的顶点和线段 的端点都在边长为1的小正方形的顶点上．‎ ‎（1）填空：　　　　．　　　　；‎ 图9‎ ‎（2）请你在图中找出一点，再连接，使以为顶点的三角形与全等，并加以证明．‎ ‎21．（本题满分6分）‎ 桌面上有4张背面相同的卡片，正面分别写着数字“1”、“2”、“3”“4”．先将卡片背面朝上洗匀．‎ ‎（1）如果让小唐从中任意抽取一张，抽到奇数的概率是　　　　；‎ ‎（2）如果让小唐从中同时抽取两张．游戏规则规定：抽到的两张卡片上的数字之和为奇数，则小唐胜，否则小谢胜．你认为这个游戏公平吗？说出你的理由．‎ ‎22．（本题满分8分）‎ 如图10，从热气球上测得两建筑物的底部的俯角分别为和，如果两建筑物的距离为，点在地面上的正投影恰好落在线段上，求热气球的高度．（结果精确到，参考数据：，）‎ 图10‎ ‎23．（本题满发8分）‎ 目前，“低碳”已成为保护地球环境的热门话题．风能是一种清洁能源，近几年我国风电装机容量迅速增长．图11是我国2003年－2009年部分年份的内力发电装机容量统计图（单位：万千瓦），观察统计图解答下列问题．‎ 图11‎ ‎（1）2007年，我国风力发电装机容量已达　　　　万千瓦；从2003年到2009年，我国风力发电装机容量平均每年增长　　　　万千瓦；‎ ‎（2）求2007～2009这两年装机容量的年平均增长率；（参考数据：，，）‎ ‎（3）按（2）的增长率，请你预测2010年我国风力发电装机容量．（结果保留到万千瓦）‎ ‎24．（本题满分10分）‎ 某住宅小区计划购买并种植甲、乙两种树苗共300株．已知甲种树苗每株60元，乙种树苗每株90元．‎ ‎（1）若购买树苗共用21000元，问甲、乙两种树苗应各买多少株？‎ ‎（2）据统计，甲、乙两种树苗每株树苗对空气的净化指数分别为和，问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和不低于90而且费用最低？‎ ‎25．（本题满分10分）‎ 如图12，为直径，且弦于，过点的切线与的延长线交于点．‎ ‎（1）若是的中点，连接并延长交于．求证：．‎ 图12‎ ‎（2）若，求的半径．‎ ‎26．（本题满分12分）‎ 如图13，过点作轴、轴的垂线，分别交轴、轴于两点，交双曲线于两点．‎ ‎（1）点的坐标是　　　　，点的坐标是　　　　；（均用含的式子表示）‎ ‎（2）判断与的位置关系，并证明你的结论；‎ 图13‎ ‎（3）记，是否有最小值？若有，求出其最小值；若没有，请说明理由．‎ ‎2010年柳州市初中毕业升学考试 数学参考答案及评分标准 第Ⅰ卷：一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A C B D A A D C C B C B 第Ⅱ卷：二、填空题 题号 ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ 答案 如，等等（答案不唯一，只要正确均可得分）‎ ‎55‎ 或 ‎1或或 ‎（说明：第17题只写对一个结果给2分，两个结果都写对给3分；第18题每写对一个结果给1分）‎ 三、解答题：‎ ‎19．本题满分6分．‎ 解：原式= 3分 ‎= 6分 ‎20．本题满分6分．‎ ‎（1），，‎ ‎ 2分 ‎（2）（说明：的位置有四处，分别是图中的．此处画出在处的位置及证明，在其余位置的画法及证明参照此法给分）‎ 解：的位置如图所示．‎ ‎ 3分 证明：‎ ‎ 4分 ‎ 5分 ‎ 6分 ‎（说明：其他证法参照此法给分）‎ ‎21．本题满分6分．‎ 解：（1） 2分 ‎（2）（方法一）‎ 这个游戏不公平． 3分 理由如下：任意抽取两个数，共有6种不同的抽法，其中和为奇数的抽法共有4种．‎ ‎（和为奇数）= 4分 ‎（和为偶数）= 5分 ‎（方法二）设2008年的风力发电装机容量为万千瓦．‎ ‎ 4分 ‎ ‎ ‎ 5分 经检验，是所列方程的根．‎ 则2007到2009这两年装机容量的年增长率为 6分 答：2007到2009这两年装机容量的年平均增长率约为124%．‎ ‎（3） 7分 ‎2010年我国风力发电装机容量约为万千瓦． 8分 ‎24．本题满分10分．‎ 解：（1）设甲种树苗买株，则乙种树苗买株． 1分 ‎ 3分 ‎ 4分 ‎ 5分 答：甲种树苗买200株，乙种树苗买100株．‎ ‎（2）设买株甲种树苗，株乙种树苗时该小区的空气净化指数之和不低于90．‎ ‎ 6分 ‎ 7分 此时费用 ‎ 8分 是的一次函数，随的增大而减少 当时，（元） 9分 即应买225株甲种树苗，75株乙种树苗时该小区的空气净化指数之和不低于90，费用最小为20250元． 10分 ‎（说明：其他解法参照此法给分）‎ ‎25．本题满分10分 ‎（1）（方法一）‎ 连接．‎ 为的直径，且于，‎ 由垂径定理得：点是的中点． 1分 又是的中点 是的中位线 2分 ‎ 3分 为直径，， 4分 即 5分 ‎（方法二）‎ ‎， 1分 是的中点，，即有 2分 又，由与同对知 ‎ 3分 又 ‎ 4分 ‎，即． 5分 ‎（方法三）‎ ‎， 1分 由于是的中点，，即有 又与同对， 2分 又 ‎ 3分 又 ‎ 4分 即有， 5分 ‎（2）连接 与同对，‎ ‎ 6分 为的切线，‎ 在中，‎ 设，则，由勾股定理得：‎ ‎ 7分 又为直径，‎ ‎ 8分 即 ‎ 9分 直径 则的半径为 10分 ‎（说明：其他解法参照此法给分）‎ ‎26．本题满分12分．‎ 解：（1）， 3分 ‎（说明：只写对一个点的坐标给2分，写对两个点的坐标给3分）‎ ‎（2）（证法一）结论： 4分 证明：，，‎ 即得： 5分 ‎ 6分 ‎ 7分 ‎（证法二）结论： 4分 证明：，，‎ 即得： 5分 在中，‎ 在中，‎ ‎ 6分 ‎ 7分 ‎（3）（方法一）‎ 有最小值 8分 ‎=‎ ‎ 9分 由（2）知，‎ ‎ 10分 ‎ 11分 又，此时的值随值增大而增大，‎ 当时，‎ 的最小值是 12分 ‎（方法二）‎ 有最小值 8分 分别过点作的平行线，交点为 由（2）知，‎ 四边形为矩形 ‎=‎ ‎= 9分 ‎= 10分 ‎=‎ ‎= 11分 又，此时的值随值增大而增大，‎ 当时，‎ 的最小值是． 12分 ‎（说明：其他解法参照此法给分）‎