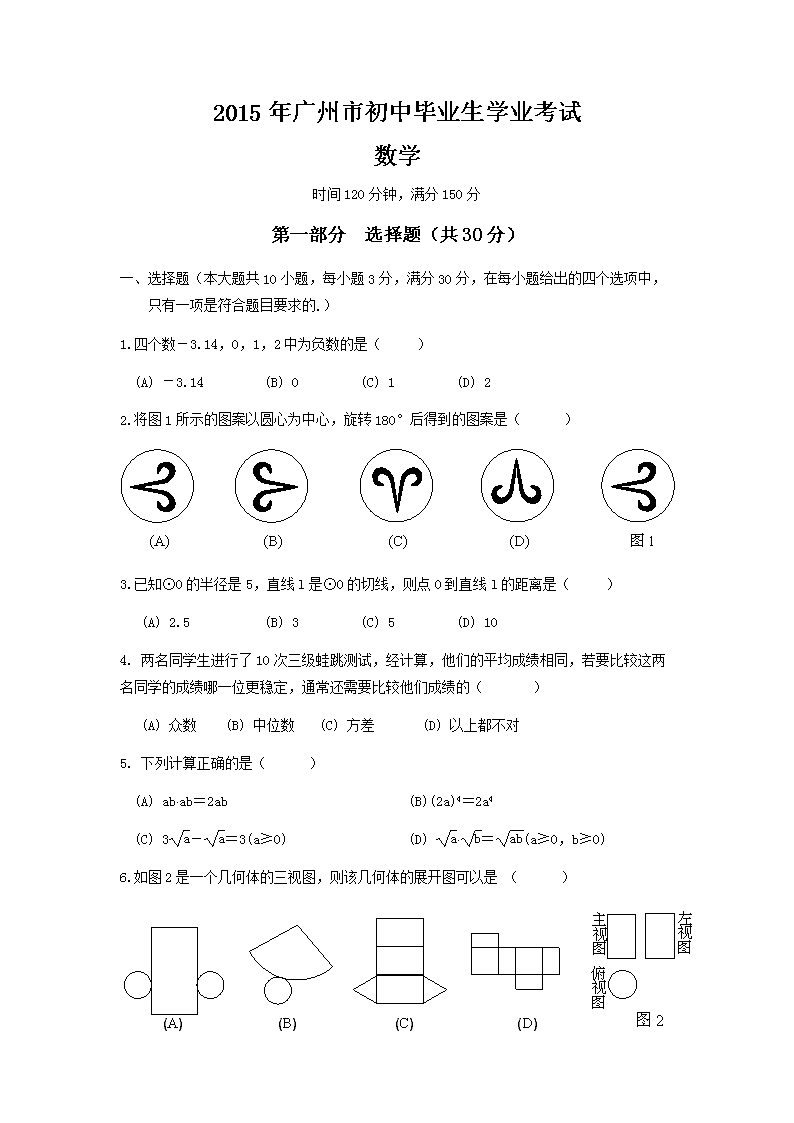
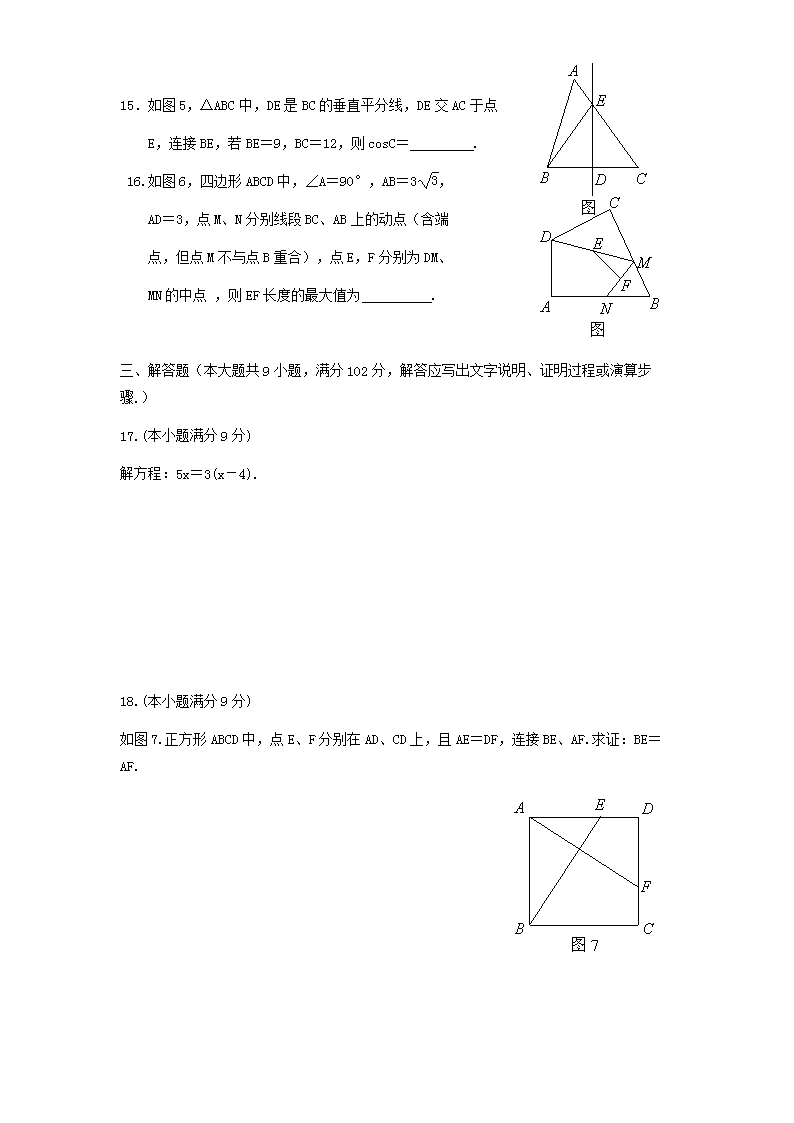
- 382.00 KB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2015年广州市初中毕业生学业考试
数学
时间120分钟,满分150分
第一部分 选择题(共30分)
一、选择题(本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.四个数-3.14,0,1,2中为负数的是( )
(A) -3.14 (B) 0 (C) 1 (D) 2
2.将图1所示的图案以圆心为中心,旋转180°后得到的图案是( )
(A)
(B)
(C)
(D)
图1
3.已知⊙O的半径是5,直线l是⊙O的切线,则点O到直线l的距离是( )
(A) 2.5 (B) 3 (C) 5 (D) 10
4. 两名同学生进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的( )
(A) 众数 (B) 中位数 (C) 方差 (D) 以上都不对
5. 下列计算正确的是( )
(A) ab×ab=2ab (B)(2a)4=2a4
(C) 3-=3(a≥0) (D) ×=(a≥0,b≥0)
6.如图2是一个几何体的三视图,则该几何体的展开图可以是 ( )
(A)
(B)
(C)
(D)
图2
主视图
左视图
俯视图
7.已知a、b满足方程组,则a+b=( )
(A) -4 (B) 4 (C) -2 (D) 2
8. 下列命题中,真命题的个数有( )
①对角线互相平分的四边形是平行四边形,
②两组对角线分别相等的四边形是平行四边形.
③一组对边平行,另一组对边相等的四边形是平行四边形.
(A) 3个 (B) 2个 (C) 1个 (D) 0个
9. 已知圆的半径是2,则该圆的内接正六边形的面积是( )
(A) 3 (B) 9 (C) 18 (D) 36
10.已知2是关于x的方程x2-2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为( )
(A) 10 (B) 14 (C) 10或14 (D) 8或10
第二部分 非选择题(共120分)
A
B
C
D
图3
l
1
2
二、填空题(本大题共6小题,每小题3分,满分18分.)
11.如图3,AB∥CD,直线l分别与AB、CD相交,若∠1=
50°,则∠2的度数为 .
其它
19%
20.6%
11.5%
21.7%
10.4%
8.6%
8.2%
生物质燃烧
扬尘
机动车尾气
工业工艺源
燃煤
生活垃圾
图4
12.根据环保局公布的广州市2013年到2014年PM2.5 的主
要来源的数据,制成扇形统计图(如图4).其中所占百
分比最大的主要来源是 (填主要来源的名称)
13.分解因式:2mx-6my= .
14.某水库的水位在5小时内持续上涨,初始的水位高度为
6米,水位以每小时0.3米的速度匀速上升,则水库的
水位高度y米与时间x小时0≤x≤5的函数关系式
为 .
A
B
C
D
E
图5
15.如图5,△ABC中,DE是BC的垂直平分线,DE交AC于点
E,连接BE,若BE=9,BC=12,则cosC= .
A
B
C
D
E
F
M
N
图6
16.如图6,四边形ABCD中,∠A=90°,AB=3,
AD=3,点M、N分别线段BC、AB上的动点(含端
点,但点M不与点B重合),点E,F分别为DM、
MN的中点 ,则EF长度的最大值为 .
三、解答题(本大题共9小题,满分102分,解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分9分)
解方程:5x=3(x-4).
18.(本小题满分9分)
如图7.正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF.求证:BE=AF.
A
D
E
B
C
F
图7
19.(本小题满分10分)
已知A=.
(1) 化简A;
(2)当A满足不等式组,且x为整数时,求A的值.
20.(本小题满分10分)
已知反比例函y=的图象的一支位于第一象限.
(1) 判断该函数图象的另一支所在的象限,并求m的取值范围;
(2) 如图8,O为坐标原点,点A在该反比例函数位第于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
A
O
B
x
y
图8
21.(本小题满分12分)
某地区2013年投入教育经费2500万元,2015年投入教育经费3025万元.
(1) 求2013年到2015年该地区投入教育经费的年平均增长率;
(2) 根据 (1) 所得的年平均增长率,预计2016年该地区将投入教育经费多少万元.
22.(本小题满分12分)
4件同型号的产品中,有1件不合格品和3件合格品.
(1) 从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2) 从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3) 在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现:抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
23.(本小题满分12分)
如图9,AC是⊙O的直径,点B在⊙O上,∠ACB=30°.
(1) 利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法)
(2) 在 (1) 所作的图形中,求△ABE与△CDE的面积之比.
A
B
C
O
图9
24.(本小题满分14分)
如图10,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
(1) 试探究筝形对角线之间的位置关系,并证明你的结论;
(2) 在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD、AC为对角线,BD=8.
①是否存在一个圆使得A、B、C、D四个点都在这个圆上?若存在,求出圆的半径;若不存在,请说明理由;
②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE,当四边形ABED为菱形时,求点F到AB的距离.
O
M
N
T
图10
25.(本小题满分14分)
已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且OC两点间的距离为3,x1×x2<0,│x1│+│ x2│=4,点A、C在直线
y2=-3x+t上.
(1) 求点C的坐标;
(2) 当y随着x的增大而增大时,求自变量x的取值范围;
(3) 当抛物线y1向左平移n(n>0) 个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2-5n的最小值.
2015广州中考数学、参考答案
一、 选择题:1-5 A D C C D 6-10 A B B C B
二、 填空题
11、50° 12、机动车尾气 13、 14、 15、 16、3
三、 简答题
17、 18、提示:证明△EAB与△FDA全等
19、(1) (2)(只能取2)时,A=1 20、(1) (2)
21、(1)10% (2)3327.5万元 22、(1) (2) (3)16
23、提示(2)设半径为R,△ABE与△DCE相似,在RT△ODC中利用勾股定理算出DC,最后求出面积比为相似比的平方等于。
24、(1)OT⊥MN
(2)①存在。提示:设AC,BD交点为M,∠ABC=∠ACB=90°,△ABM与△ACB相似,可求得半径等于。
②提示:作FG⊥AB,交AB与点G,△BME与△BFD相似,求出DF=,再△BGF与△EFD相似,可求出P到AB的距离FG等于
25、 提示:(1)
(2) ①若C(0,3),,时,随着的增大而增大
②若C(0,-3),,时,随着的增大而增大
(2) ①若,平移后
平移后,要使得有公共点,则当,
求得(不符合,舍去)
②若,平移后
平移后,要使得有公共点,则当, 求得
,当时,最小值为