2011年福建省莆田市中考数学试题及答案 9页

‎2011年莆田中考数学试题 一、 精心选一选：本大题共8小题，每每小题4分，共32分。‎ ‎1. 的相反数是（ ）‎ ‎ A． B． C． 2011 D． ‎ ‎2. 下列运算哪种，正确的是（ ）‎ ‎ A． B． C． D．‎ ‎3. 已知点P（）在平面直角坐标系的第一象限内，则a的取值范围在数轴上可表示为（ ）‎ ‎ ‎ ‎4. 在平行四边形、等边三角形、菱形、等腰梯形中既是轴对称图形又是中心对称图形的是（ ）‎ A． 平行四边形 B． 等边三角形 C．菱形 D．等腰梯形 ‎5. 抛物线可以看作是由抛物线按下列何种变换得到（ ）‎ A． 向上平移5个单位 B． 向下平移5个单位 ‎ C． 向左平移5个单位 D． 向右平移5个单位 ‎6. 如图所示的是某几何体的三视图，则该几何体的形状是（ ）‎ ‎ A． 长方体 B．三棱柱 C．圆锥 D．正方体 ‎7. 等腰三角形的两条边长分别为3,6，那么它的周长为（ ）‎ ‎ A．15 B．‎12 ‎ C．12或15 D．不能确定 ‎8. 如图，在矩形ABCD中，点E在AB边上，沿CE折叠矩形ABCD，使点B落在 AD边上的点F处，若AB=4，BC=5，则tan∠AFE的值为（ ）‎ ‎ A． B． C． D．‎ 二、 细心填一填：本大题共8小题，每小题4分，共32分）‎ ‎9. 一天有86400秒，用科学记数法表示为____________ 秒；‎ ‎10．数据的平均数是1，则这组数据的中位数是_________。‎ ‎11. ⊙和⊙的半径分别为3㎝和4㎝，若⊙和⊙相外切，则圆心距 =_________cm。‎ ‎12. 若一个正多边形的一个外角等于40°，则这个多边形是_________边形。‎ ‎13. 在围棋盒中有6颗黑色棋子和a颗白色棋子，随机地取出一颗棋子，如果它是黑色棋子的概率是，则a=________。‎ ‎14. 如图，线段AB、DC分别表示甲、乙两座楼房的高，AB⊥BC，DC⊥BC，两建筑物间距离BC=‎30米，若甲建筑物高AB=‎28米，在点A测得D点的仰角α=45°，则乙建筑物高DC=_______米。‎ ‎15. 如图，一束光线从点A（3, 3）出发，经过y轴上的点C反射后经过点B（1, 0），‎ 则光线从A到B点经过的路线长是_______。‎ ‎16. 已知函数，其中表示当时对应的函数值，‎ 如，‎ 则=_______。‎ 三．耐心填一填：本大题共9小题，共86分，解答时应写出必要的文字说明、‎ 证明过程或演算步骤。‎ ‎17. （本小题满分8分）‎ ‎ 计算：‎ ‎18．（本小题满分8分）‎ ‎ 化简求值：，其中。‎ ‎19. (本小题满分8分)‎ ‎ 如图．在△ABC中．D是AB的中点．E是CD的中点．‎ 过点C作CF∥AB交AE的延长线于点F．连接BF。‎ ‎（1）(4分)求证：DB=CF；‎ ‎（2）(4分)如果AC=BC．试判断四边彤BDCF的形状．‎ ‎ 并证明你的结论。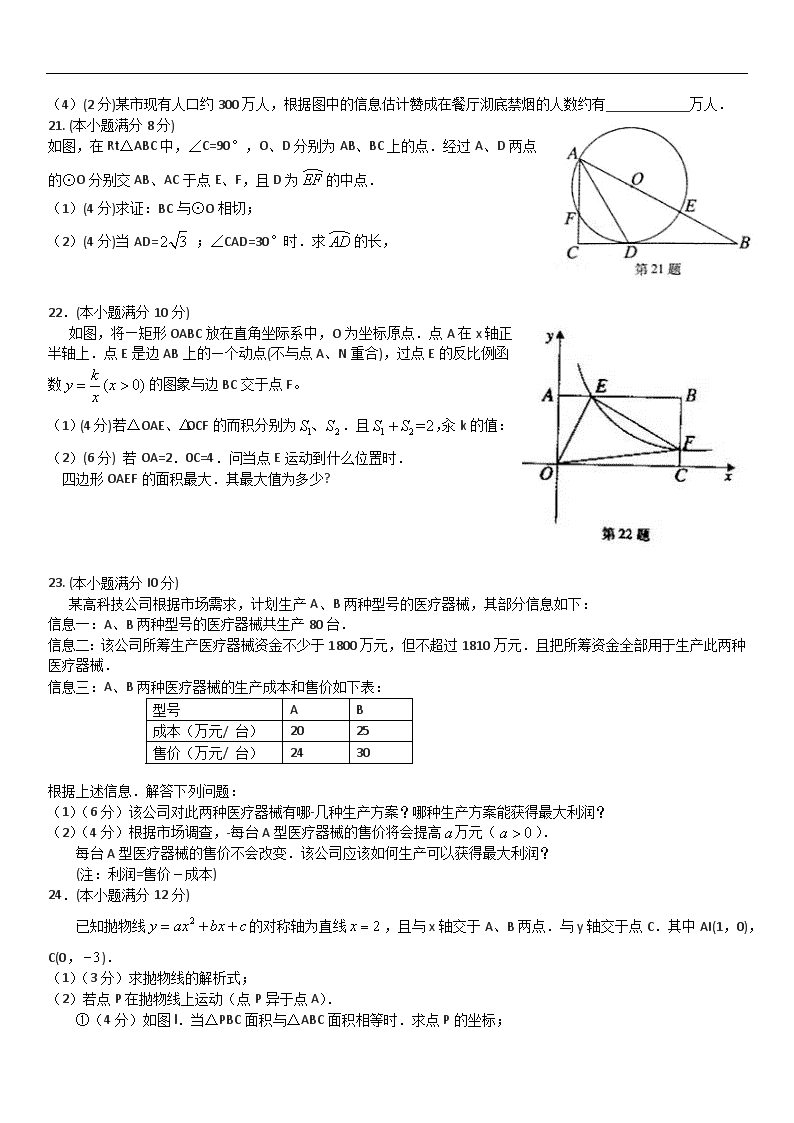‎ ‎20．(本小题满分8分)‎ ‎ “国际无烟日”来临之际．小敏同学就一批公众对在餐厅吸烟所持的三种态度(彻底禁烟、建立吸烟室、其他)进行了调查．并把调查结果绘制成如图1、2的统计图．请根据下面图中的信息回答下列问题：‎ ‎（1）(2分)被调查者中，不吸烟者中赞成彻底禁烟的人数有____________人：‎ ‎（2）(2分)本次抽样凋查的样本容量为____________‎ ‎（3）(2分)被调查者中．希望建立吸烟室的人数有____________；‎ ‎（4）(2分)某市现有人口约300万人，根据图中的信息估计赞成在餐厅沏底禁烟的人数约有____________万人．‎ ‎21. (本小题满分8分)‎ 如图，在Rt△ABC中，∠C=90°，O、D分别为AB、BC上的点．经过A、D两点的⊙O分别交AB、AC于点E、F，且D为的中点．‎ ‎（1）(4分)求证：BC与⊙O相切；‎ ‎（2）(4分)当AD= ；∠CAD=30°时．求的长，‎ ‎22．(本小题满分10分)‎ ‎ 如图，将—矩形OABC放在直角坐际系中，O为坐标原点．点A在x轴正半轴上．点E是边AB上的—个动点(不与点A、N重合)，过点E的反比例函数的图象与边BC交于点F。‎ ‎（1）(4分)若△OAE、△OCF的而积分别为．且，汆k的值：‎ ‎（2）(6分) 若OA=2．0C=4．问当点E运动到什么位置时．‎ ‎ 四边形OAEF的面积最大．其最大值为多少?‎ ‎23. (本小题满分I0分)‎ ‎ 某高科技公司根据市场需求，计划生产A、B两种型号的医疗器械，其部分信息如下：‎ 信息一：A、B两种型号的医疔器械共生产80台．‎ 信息二：该公司所筹生产医疗器械资金不少于1800万元，但不超过1810万元．且把所筹资金全部用于生产此两种医疗器械．‎ 信息三：A、B两种医疗器械的生产成本和售价如下表：‎ 型号 A B 成本（万元/ 台）‎ ‎20‎ ‎25‎ 售价（万元/ 台）‎ ‎24‎ ‎30‎ 根据上述信息．解答下列问题：‎ ‎（1）（6分）该公司对此两种医疗器械有哪-几种生产方案？哪种生产方案能获得最大利润？‎ ‎（2）（4分）根据市场调查，-每台A型医疗器械的售价将会提高万元（）．‎ ‎ 每台A型医疗器械的售价不会改变．该公司应该如何生产可以获得最大利润？‎ ‎ (注：利润=售价成本)‎ ‎24．(本小题满分12分)‎ ‎ 已知抛物线的对称轴为直线，且与x轴交于A、B两点．与y轴交于点C．其中AI(1，0)，C(0，)．‎ ‎（1）（3分）求抛物线的解析式；‎ ‎（2）若点P在抛物线上运动（点P异于点A）．‎ ‎ ①（4分）如图l．当△PBC面积与△ABC面积相等时．求点P的坐标；‎ ‎②（5分）如图2．当∠PCB=∠BCA时，求直线CP的解析式。‎ ‎25.(本小题满分14分)‎ ‎ 已知菱形ABCD的边长为1．∠ADC=60°，等边△AEF两边分别交边DC、CB于点E、F。‎ ‎（1）（4分）特殊发现：如图1，若点E、F分别是边DC、CB的中点．求证：菱形ABCD对角线AC、BD交点O即为等边△AEF的外心；‎ ‎（2）若点E、F始终分别在边DC、CB上移动．记等边△AEF的外心为点P．‎ ‎ ①（4分）猜想验证：如图2．猜想△AEF的外心P落在哪一直线上，并加以证明；‎ ‎ ②（6分）拓展运用：如图3，当△AEF面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，试判断是否为定值．若是．请求出该定值；若不是．请说明理由。‎ ‎2011年莆田市初中毕业、升学考试试卷 数学参考答案及评分标准 一、精心选一选 ‎ 1．C 2．D 3．A 4．C 5．B 6，B 7．A 8．C 二、耐心填—填 ‎ 9． I0．1 1I．7 12，9 13．4 14，58 15，5 16．5151‎ 三，耐心填一填 ‎17．解：原式=4‎ ‎18. 原式=，当时，原式=18‎ ‎19. （1）证明略 （2）四边形BDCF是矩形。证明略。‎ ‎20. （1）证明：连接OD，则OD=OA，‎ ‎∴∠OAD=∠ODA ‎∵D为的中点 ‎∴∠OAD=∠CAD ‎∴∠ODA=∠CAD ‎∴OD∥AC 又∵∠C=90°，∴∠ODC=90°，即BC⊥OD ‎∴BC与⊙O相切。‎ ‎（2）连接DE，则∠ADE=90°‎ ‎∵∠OAD=∠ODA=∠CAD=30°，∴∠AOD=120°‎ 在Rt△ADE中，易求AE=4，‎ ‎∴⊙O的半径r=2‎ ‎∴的长。‎ ‎22. 解：（1）∵点E、F在函数的图象上，‎ ‎∴设，‎ ‎∴，‎ ‎∵，∴，。‎ ‎（2）∵四边形OABC为矩形，OA=2，OC=4，‎ 设，‎ ‎∴BE=，BF=‎ ‎∴‎ ‎∵，‎ ‎∴‎ ‎=‎ ‎∴当时，，∴AE=2.‎ 当点E运动到AB的中点时，四边形OAEF的面积最大，最大值是5.‎ ‎23.解：（1）设该公司生产A钟中医疗器械x台，则生产B钟中医疗器械（）台，依题意得 解得，‎ 取整数得 ‎∴该公司有3钟生产方案：‎ 方案一：生产A钟器械38台，B钟器械42台。‎ 方案二：生产A钟器械39台，B钟器械41台。‎ 方案一：生产A钟器械40台，B钟器械40台。‎ 公司获得利润：‎ 当时，有最大值。‎ ‎∴当生产A钟器械38台，B钟器械42台时获得最大利润。‎ ‎（2）依题意得，‎ 当，即时，生产A钟器械40台，B钟器械40台，获得最大利润。‎ 当，即时，（1）中三种方案利润都为400万元；‎ 当，即时，生产A钟器械38台，B钟器械42台，获得最大利润。‎ ‎24. 解：（1）由题意，得，解得 ‎∴抛物线的解析式为。‎ ‎（2）①令，解得 ∴B（3, 0）‎ 当点P在x轴上方时，如图1，‎ 过点A作直线BC的平行线交抛物线于点P，‎ 易求直线BC的解析式为，‎ ‎∴设直线AP的解析式为，‎ ‎∵直线AP过点A（1,0），代入求得。‎ ‎∴直线AP的解析式为 解方程组，得 ‎∴点 当点P在x轴下方时，如图1‎ 设直线交y轴于点，‎ 把直线BC向下平移2个单位，交抛物线于点，‎ 得直线的解析式为，‎ 解方程组，得 ‎∴‎ 综上所述，点P的坐标为：，‎ ‎②∵‎ ‎∴OB=OC，∴∠OCB=∠OBC=45°‎ 设直线CP的解析式为 如图2，延长CP交x轴于点Q，‎ 设∠OCA=α，则∠ACB=45°α ‎∵∠PCB=∠BCA ∴∠PCB=45°α ‎∴∠OQC=∠OBC-∠PCB=45°-（45°α）=α ‎∴∠OCA=∠OQC 又∵∠AOC=∠COQ=90°‎ ‎∴Rt△AOC∽Rt△COQ ‎∴，∴，∴OQ=9，∴‎ ‎∵直线CP过点，∴‎ ‎∴‎ ‎∴直线CP的解析式为。‎ 其它方法略。‎ ‎25．解：（1）证明：如图I，分别连接OE、‎‎0F ‎ ∵四边形ABCD是菱形 ‎ ∴AC⊥BD，BD平分∠ADC．AO=DC=BC ‎ ∴∠COD=∠COB=∠AOD=90°．‎ ‎ ∠ADO=∠ADC=×60°=30°‎ ‎ 又∵E、F分别为DC、CB中点 ‎ ∴OE=CD，OF=BC，AO=AD ‎ ∴0E=OF=OA ∴点O即为△AEF的外心。‎ ‎ （2）①猜想：外心P一定落在直线DB上。‎ ‎ 证明：如图2，分别连接PE、PA，过点P分别作PI⊥CD于I，P J⊥AD于J ‎∴∠PIE=∠PJD=90°，∵∠ADC=60°‎ ‎∴∠IPJ=360°-∠PIE-∠PJD-∠JDI=120°‎ ‎∵点P是等边△AEF的外心，∴∠EPA=120°，PE=PA，‎ ‎∴∠IPJ=∠EPA，∴∠IPE=∠JPA ‎∴△PIE≌△PJA， ∴PI=PJ ‎∴点P在∠ADC的平分线上，即点P落在直线DB上。‎ ‎②为定值2.‎ 当AE⊥DC时．△AEF面积最小，‎ 此时点E、F分别为DC、CB中点．‎ 连接BD、AC交于点P，由（1）‎ 可得点P即为△AEF的外心 解法一：如图3．设MN交BC于点G 设DM=x，DN=y(x≠0．y≠O)，则 CN=‎ ‎∵BC∥DA ∴△GBP∽△MDP．∴BG=DM=x．‎ ‎∴‎ ‎∵BC∥DA，∴△GBP∽△NDM ‎∴，∴‎ ‎∴‎ ‎∴，即 其它解法略。‎