中考数学综合题专题动点综合型问题二专题解析 42页

中考数学综合题专题【动点综合型问题二】专题解析 ‎23．（江苏连云港）如图，甲、乙两人分别从A（1，）、B（6，0）两点同时出发，点O为坐标原点．甲沿AO方向、乙沿BO方向均以4km/h的速度行走，t h后，甲到达M点，乙到达N点．‎ ‎（1）请说明甲、乙两人到达O点前，MN与AB不可能平行．‎ ‎（2）当t为何值时，△OMN∽△OBA？‎ O B y x A ‎（3）甲、乙两人之间的距离为MN的长，设s＝MN 2，求s与t之间的函数关系式，并求甲、乙两人之间距离的最小值．‎ 解：（1）∵A（1，），∴OA＝2，∠AOB＝60°‎ 假设MN∥AB，则有 ＝ ‎∵OM＝2－4t，ON＝6－4t，∴ ＝ 解得t＝0‎ 即在甲、乙两人到达O点前，只有当t＝0时，△OMN∽△OAB ‎∴MN与AB不可能平行 ‎（2）∵甲达到O点时间为t＝ ＝ ，乙达到O点时间为t＝ ＝ ‎∴甲先到达O点，∴t＝ 或t＝ 时，O、M、N三点不能构成三角形 ‎①当t ＜ 时，若△OMN∽△OBA，则有 ＝ 解得t＝2＞ ，∴△OMN与△OBA不相似 O B y x A M H 图1‎ N ‎②当 ＜t ＜ 时，∠MON＞∠OAB，显然△OMN与△OBA不相似 ‎③当t ＞ 时， ＝ ，解得t＝2＞ ‎∴当t＝2时，△OMN∽△OBA ‎（3）①当t ≤ 时，如图1，过点M作MH⊥x轴，垂足为H 在Rt△MOH中，∵∠AOB＝60°‎ ‎∴MH＝OM·sin60°＝( 2－4t )× ＝( 1－2t )‎ ‎∴NH＝ ( 4t－2 )＋( 6－4t )＝5－2t O B y x A M H 图2‎ N ‎∴s＝[ ( 1－2t )]2＋( 5－2t )2＝16t 2－32t＋28‎ ‎②当 ＜t ≤ 时，如图2，作MH⊥x轴，垂足为H 在Rt△MNH中，MH＝ ( 4t－2 )＝( 2t－1 )‎ NH＝ ( 4t－2 )＋( 6－4t )＝5－2t ‎∴s＝[ ( 1－2t )]2＋( 5－2t )2＝16t 2－32t＋28‎ ‎③当t ＞ 时，同理可得s＝[ ( 1－2t )]2＋( 5－2t )2＝16t 2－32t＋28‎ 综上所述，s＝16t 2－32t＋28‎ ‎∵s＝16t 2－32t＋28＝16( t－1 )2＋12‎ ‎∴当t＝1时，s有最小值为12‎ ‎∴甲、乙两人距离的最小值为2km ‎24．（江苏南通）如图，在△ABC中，AB＝AC＝10厘米，BC＝12厘米，D是BC的中点．点P从B出发，以a厘米/秒（a＞0）的速度沿BA匀速向点A运动，点Q同时以1厘米/秒的速度从D出发，沿DB匀速向点B运动，其中一个动点到达端点时，另一个动点也随之停止运动，设它们运动的时间为t秒．‎ ‎（1）若a＝2，△BPQ∽△BDA，求t的值；‎ ‎（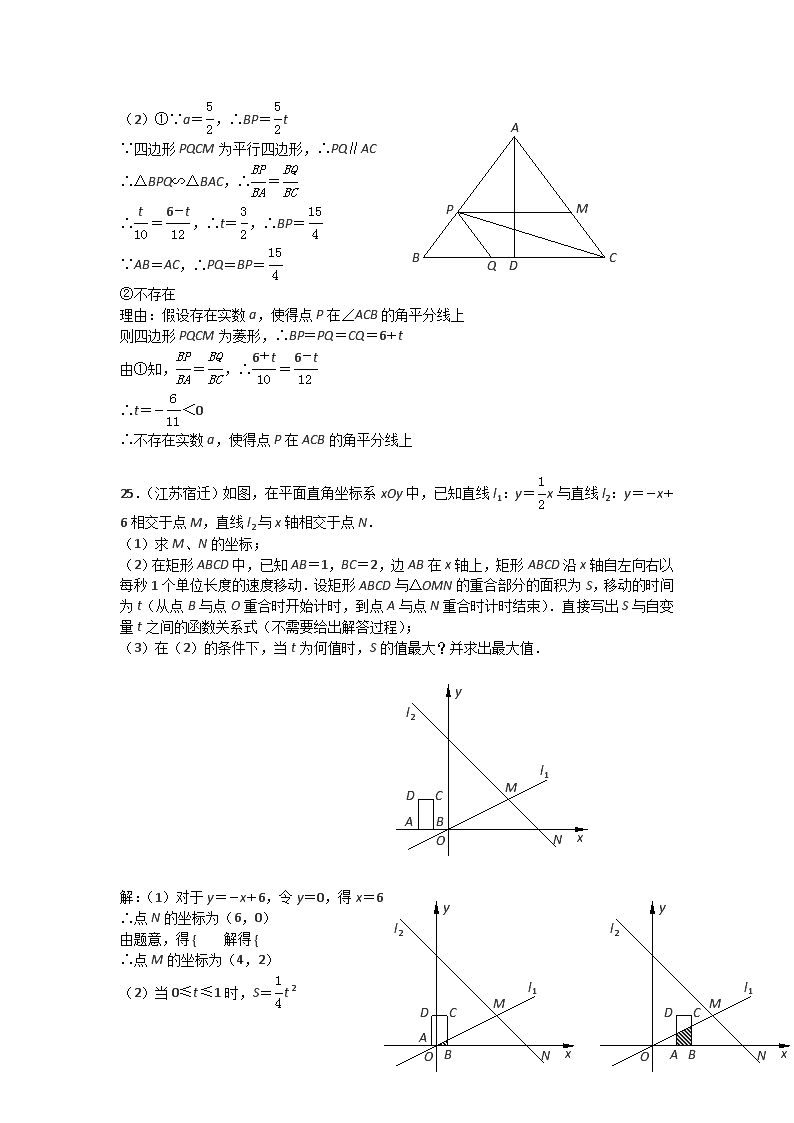2）设点M在AC上，四边形PQCM为平行四边形．‎ ‎①若a＝ ，求PQ的长；‎ ‎②是否存在实数a，使得点P在∠ACB的平分线上？若存在，请求出a的值；若不存在，请说明理由．‎ C B D A Q P 解：（1）∵BC＝12，D是BC的中点 ‎∴BD＝CD＝6‎ ‎∵a＝2，∴BP＝2t，DQ＝t，BQ＝6－t ‎∵△BPQ∽△BDA，∴ ＝ ‎∴ ＝ ，∴t＝ C B D A Q P M ‎（2）①∵a＝ ，∴BP＝ t ‎∵四边形PQCM为平行四边形，∴PQ∥AC ‎∴△BPQ∽△BAC，∴ ＝ ‎∴ ＝ ，∴t＝ ，∴BP＝ ‎∵AB＝AC，∴PQ＝BP＝ ‎②不存在 理由：假设存在实数a，使得点P在∠ACB的角平分线上 则四边形PQCM为菱形，∴BP＝PQ＝CQ＝6＋t 由①知， ＝ ，∴ ＝ ‎∴t＝－ ＜0‎ ‎∴不存在实数a，使得点P在ACB的角平分线上 ‎25．（江苏宿迁）如图，在平面直角坐标系xOy中，已知直线l1：y＝ x与直线l2：y＝－x＋6相交于点M，直线l2与x轴相交于点N．‎ ‎（1）求M、N的坐标；‎ ‎（2）在矩形ABCD中，已知AB＝1，BC＝2，边AB在x轴上，矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动．设矩形ABCD与△OMN的重合部分的面积为S，移动的时间为t（从点B与点O重合时开始计时，到点A与点N重合时计时结束）．直接写出S与自变量t之间的函数关系式（不需要给出解答过程）；‎ ‎（3）在（2）的条件下，当t为何值时，S的值最大？并求出最大值．‎ A B l1‎ N M x l2‎ C D y O A l1‎ N M x l2‎ C D y O B A B l1‎ N M x l2‎ C D y O 解：（1）对于y＝－x＋6，令y＝0，得x＝6‎ ‎∴点N的坐标为（6，0）‎ 由题意，得 解得 ‎∴点M的坐标为（4，2）‎ ‎（2）当0≤t ≤1时，S＝ t 2‎ 当1＜t ≤4时，S＝ t－ A l1‎ N M x l2‎ C D y O B A l1‎ N M x l2‎ C D y O B 当4＜t ＜5时，S＝－ t 2＋ t－ 当5≤t ＜6时，S＝－t＋ 当6≤t ≤7时，S＝ ( 7－t )2‎ ‎（3）解法一：当0≤t ≤1时，S最大＝ 当1＜t ≤4时，S最大＝ A l1‎ N M x l2‎ C D y O B 当4＜t ＜5时，S＝－ ( t－ )2＋ ‎∴当t＝ 时，S最大＝ 当5≤t ＜6时，S最大＝ 当6≤t ≤7时，S最大＝ 综上可知，当t＝ 时，S的值最大，且最大值是 解法二：由（2）中的函数关系式可知，S的最大值一定在4＜t ＜5时取得 当4＜t ＜5时，S＝－ ( t－ )2＋ ‎∴当t＝ 时，S的值最大，且最大值是 ‎26．（江苏模拟）已知抛物线与x轴交于B、C（1，0）两点，与y轴交于点A，顶点坐标为（ ，－ ）．P、Q分别是线段AB、OB上的动点，它们同时分别从点A、O向B点匀速运动，速度均为每秒1个单位，设P、Q运动时间为t（0≤t≤4）．‎ ‎（1）求此抛物线的解析式，并求出P点的坐标（用t表示）；‎ ‎（2）当△OPQ面积最大时求△OBP的面积；‎ ‎（3）当t为何值时，△OPQ为直角三角形？‎ ‎（4）△OPQ是否可能为等边三角形？若可能请求出t的值；若不可能请说明理由，并改变Q点的运动速度，使△OPQ为等边三角形，求出Q点运动的速度和此时t的值．‎ y O x A B C Q P 解：（1）设抛物线的解析式为y＝a( x－ )2－ ‎∵抛物线过点C（1，0）‎ ‎∴0＝a( 1－ )2－ ，∴a＝ ‎∴y＝ ( x－ )2－ 令y＝0，得x1＝1，x2＝4，∴B（4，0）‎ 令x＝0，得y＝3，∴A（0，3）‎ O x A B C Q P y M N ‎∴AB＝ ＝5‎ 过点P作PM⊥y轴于M 则△AMP∽△AOB，∴ ＝ ＝ 即 ＝ ＝ ，∴AM＝ t，PM＝ t ‎∴P（ t，3－ t）‎ ‎（2）过点P作PN⊥x轴于N ‎∴S△OPQ ＝ OQ·PN＝ ·t·( 3－ t )‎ ‎＝－ t 2＋ t＝－ ( t－ )2＋ ‎∴当t＝ 时，△OPQ面积最大 此时OP为AB边上的中线 ‎∴S△OBP ＝ S△AOB ＝ ××3×4＝3‎ ‎（3）若∠OPQ＝90°，则OP 2＋PQ 2＝OQ 2‎ ‎∴( t )2＋( 3－ t )2＋( t－ t )2＋( 3－ t )2＝t 2‎ 解得t1＝3，t2＝15（舍去）‎ 若∠OQP＝90°，则PM＝OQ ‎∴ t＝t，∴t＝0（舍去）‎ ‎∴当t＝3时，△OPQ为直角三角形 ‎（4）∵OP 2＝( t )2＋( 3－ t )2，PQ 2＝( t－ t )2＋( 3－ t )2‎ ‎∴OP≠PQ，∴△OPQ不可能是等边三角形 设Q的速度为每秒k个单位时，△OPQ为等边三角形 则OQ＝2PM，∴kt＝2· t，得k＝ PN＝ OP＝ OQ，∴3－ t＝ · t ‎∴t＝ ‎27．（江苏模拟）如图，在梯形纸片ABCD中，BC∥AD，∠A＋∠D＝90°，tanA＝2，过点B作BH⊥AD于H，BC＝BH＝2．动点F从点D出发，以每秒1个单位的速度沿DH运动到点H停止，在运动过程中，过点F作FE⊥AD交折线D－C－B于点E，将纸片沿直线EF折叠，点C、D的对应点分别是点C1、D1．设F点运动的时间是t（秒）．‎ ‎（1）当点E和点C重合时，求t的值；‎ ‎（2）在整个运动过程中，设△EFD1或四边形EFD1C1与梯形ABCD重叠部分面积为S，求S与t之间的函数关系式和相应自变量t的取值范围；‎ ‎（3）平移线段CD，交线段BH于点G，交线段AD于点P．在直线BC上是否存在点Q，使△PGQ为等腰直角三角形？若存在，求出线段BQ的长；若不存在，说明理由．‎ D1‎ A B C F E D H A B C D H 备用图 解：（1）过点C作CK⊥AD于K A B C D H K 则四边形BHKC是矩形，∴HK＝BC＝2，CK＝BH＝2‎ 在Rt△CKD中，∠DCK＋∠D＝90°‎ ‎∵∠A＋∠D＝90°，∴∠DCK＝∠A ‎∴tan∠DCK＝tanA＝2，即 ＝2‎ ‎∴DK＝4，即t＝4‎ D1‎ A B C F E D H ‎（2）∵ ＝tanA＝2，BH＝2，∴AH＝1‎ ‎∴AD＝AH＋HK＋DK＝1＋2＋4＝7‎ ‎①当0＜t ≤3.5时，重叠部分为△EFD1‎ 由题意，D1F＝DF＝t 在Rt△EFD中，∠DEF＋∠D＝90°‎ ‎∵∠A＋∠D＝90°，∴∠DEF＝∠A D1‎ A B C F E D H N M ‎∴tan∠DEF＝tanA＝2，即 ＝2，∴EF＝ t ‎∴S＝S△EFD1 ＝ D1F·EF＝ t· t＝ t 2‎ ‎②当3.5＜t ≤4时，重叠部分为四边形AFEM 过点M作MN⊥AD于N D1‎ A B C F E D H N M C1‎ 则tanA＝D1A＝2t－7， ＝tanA＝2，得AN＝ MN ＝tanD1＝tanD＝cotA＝ 即 ＝ ，得MN＝ ( 2t－7 )‎ D1‎ A B C F E D H C1‎ ‎∴S＝S△EFD1 － S△MD1A ＝ t 2－ ( 2t－7 )·( 2t－7 )‎ ‎＝－ t 2＋ t－ ‎③当4＜t ≤5时，重叠部分为五边形AFEC1M S＝S△C1D1FE － S△MD1A ＝ ( t－4＋t )·2－ ( 2t－7 )·( 2t－7 )‎ ‎＝－ t 2＋ t－ A B C D H P O Q G ‎④当5＜t ≤6时，重叠部分为梯形AFEB S＝S梯形AFEB ＝ ( 6－t＋7－t )·2＝－2t＋13‎ ‎（3）①当点P为直角顶点时 A B C D H P O G ‎(Q)‎ 作QO⊥AD于O，则∠GPH＋∠QPO＝90°‎ ‎∵∠GPH＋∠PGH＝90°，∴∠PGH＝∠QPO 又∵PG＝PQ，∠GHP＝∠POQ＝90°‎ ‎∴△GHP≌△POQ，∴HP＝OQ＝2，PO＝ OQ＝1‎ ‎∴BQ＝HO＝3‎ A B C D H P G Q ‎②当点Q为直角顶点时 同①可证△BQG≌△OQP，∴BQ＝OQ＝2‎ ‎③当点G为直角顶点时 同①可证△BQG≌△HGP，∴BG＝HP＝2GH＝2BQ ‎∵BG＋GH＝BH，∴2BQ＋BQ＝2，∴BQ＝ ‎∴在直线BC上存在点Q，使△PGQ为等腰直角三角形，线段BQ的长为3，2， ‎28．（江苏模拟）如图1，直线l：y＝－ x＋3分别交x轴、y轴于B、A两点，等腰Rt△CDE的斜边CD在x轴上，且CD＝6．若直线l以每秒3个单位的速度向上匀速运动，同时点C从（6，0）开始以每秒2个单位的速度向右匀速运动（如图2），设运动后直线l分别交x轴、y轴于N、M两点，以OM、ON为边作如图所示的矩形OMPN．设运动时间为t秒．‎ ‎（1）运动t秒后点E坐标为______________，点N坐标为______________（用含t的代数式表示）；‎ ‎（2）设矩形OMPN与运动后的△CDE的重叠部分面积为S，求S与t的函数关系式，并写出相应的t的取值范围；‎ ‎（3）若直线l和△CDE运动后，直线l上存在点Q使∠OQC＝90°，则当在线段MN上符合条件的点Q有且只有两个时，求t的取值范围；‎ ‎（4）连接PC、PE，当△PCE是等腰三角形时，直接写出t的值．‎ N M x C y O P D l E 图2‎ A B x C D y O E l 图1‎ 解：（1）E（9＋2t，3），N（4＋4t，0）‎ ‎（2）运动t秒时，ON＝4＋4t，OC＝6＋2t，OD＝12＋2t 当点N与点C重合时，4＋4t＝6＋2t，得t＝1‎ 当点E在边PN上时，4＋4t＝9＋2t，得t＝2.5‎ 当点N与点D重合时，4＋4t＝12＋2t，得t＝4‎ ‎①当1＜t ≤2.5时，重叠部分为等腰Rt△CFN CN＝FN＝4＋4t－( 6＋2t )＝2t－2‎ ‎∴S＝ ( 2t－2 )2＝2t 2－4t＋2‎ ‎②当2.5＜t ＜4时，重叠部分为四边形CEGN ND＝12＋2t－( 4＋4t )＝8－2t ‎∴S＝S△CDE － S△NGD ＝ ×6×3－ ( 8－2t )2＝－2t 2＋16t－23‎ ‎③当t ≥4时，重叠部分为△CDE N M x C y O P D l E G ‎∴S＝ ×6×3＝9‎ x C D y O E l N M F P ‎（3）①当直线l过点C，即C、N重合时，则线段MN上只存在一点Q使∠OQC＝90°‎ 由（2）知，此时t＝1‎ ‎②以OC为直径作⊙O′，当直线l切⊙O′ 于点Q时，则线段MN上只存在一点Q使∠OQC＝90°‎ N x D y O E l M ‎(C)‎ Q OO′＝O′Q＝ OC＝3＋t O′N＝ON－OO′＝4＋4t－(3＋t )＝1＋3t 由 ＝sin∠O′NQ＝sin∠MNO＝ 得 ＝ ，解得t＝3‎ 所以当在线段MN上符合条件的点Q有且只有两个时，t的取值范围是1＜t ＜3‎ C x D y O E l M Q N O′‎ ‎（4）t＝ ，t＝ ，t＝ ，t＝1‎ 提示：∵P（4＋4t，3＋3t），C（6＋2t，0），E（9＋2t，3）‎ ‎∴PC 2＝( 2t－2 )2＋( 3＋3t )2‎ PE 2＝( 2t－5 )2＋( 3t )2，CE 2＝18‎ 若PC＝PE，则( 2t－2 )2＋( 3＋3t )2＝( 2t－5 )2＋( 3t )2‎ 解得t＝ 若PC＝CE，则( 2t－2 )2＋( 3＋3t )2＝18‎ 解得t＝ （舍去负值）‎ 若PE＝CE，则( 2t－5 )2＋( 3t )2＝18‎ 解得t＝1或t＝ ‎29．（江苏模拟）如图，抛物线y＝ax 2＋bx＋c的顶点为C（0，－），与x轴交于点A、B（A在B的左侧），连接AC、BC，得等边△ABC．点P从点B出发，以每秒1个单位的速度向点A运动，同时点Q从点C出发，以每秒 个单位的速度向y轴负方向运动，连接PQ交射线BC于点D，当点P到达点A时，点Q停止运动．设运动时间为t秒．‎ ‎（1）求抛物线的解析式；‎ ‎（2）设△PQC的面积为S，求S关于t的函数关系式；‎ ‎（3）以点P为圆心，PB为半径的圆与射线BC交于点E，试说明：在点P运动的过程中，线段DE的长是一定值，并求出该定值．‎ A C O B Q x y P A C O B x y 备用图 解：（1）∵抛物线y＝ax 2＋bx＋c的顶点为C（0，－）‎ A C O B D x H Q P E y ‎∴抛物线的对称轴是y轴，∴b＝0‎ 可设抛物线的解析式为y＝ax 2－ ‎∵△ABC是等边三角形，且CO⊥AB，CO＝ ‎∴AO＝1，∴A（－1，0）‎ 把A（－1，0）代入y＝ax 2－，得a＝ ‎∴抛物线的解析式为y＝x 2－ ‎（2）当0＜t ＜1时，OP＝1－t，CQ＝t ‎∴S＝ CQ·OP＝ ·t·( 1－t )＝－ t 2＋ t 当1＜t ＜2，OP＝t－1，CQ＝t ‎∴S＝ CQ·OP＝ ·t·( t－1 )＝ t 2－ t ‎（3）连接PE，过D作DH⊥y轴于H，设DH＝a ‎①当0＜t ＜1时 ‎∵PB＝PE，∠PBE＝60°‎ ‎∴△PBE为等边三角形 A C O B H x D Q P E y ‎∴BE＝PB＝t ‎∵△QDH∽△QPO ‎∴ ＝ ，即 ＝ ‎∴a＝ ，∴DC＝1－t ‎∴DE＝CB－EB－DC＝2－t－( 1－t )＝1‎ ‎②当1＜t ＜2时 同理，△QDH∽△QPO，得 ＝ ‎∴ ＝ ‎∴a＝ ，∴DC＝t－1‎ ‎∴DE＝DC＋CE＝t－1＋( 2－t )＝1‎ 综上所述，在点P运动的过程中，线段DE的长是定值2‎ ‎30．（河北）如图，点A（－5，0），B（－3，0），点C在y轴的正半轴上，∠CBO＝45°，CD∥AB，∠CDA＝90°．点P从点Q（4，0）出发，沿x轴向左以每秒1个单位长的速度运动，运动时间为t秒．‎ ‎（1）求点C的坐标；‎ ‎（2）当∠BCP＝15°，求t的值；‎ B A Q x P O y C D ‎（3）以点P为圆心，PC为半径的⊙P随点P的运动而变化，当⊙P与四边形ABCD的边（或边所在的直线）相切时，求t的值．‎ 解：（1）∵∠BCO＝∠CBO＝45°，∴OC＝OB＝3‎ 又∵点C在y轴的正半轴上，∴点C的坐标为（0，3）‎ ‎（2）当点P在点B右侧时，如图2‎ 若∠BCP＝15°，得∠PCO＝30°‎ 故OP＝OC·tan30°＝ 此时t＝4＋ 当点P在点B左侧时，如图3‎ 由∠BCP＝15°，得∠PCO＝60°‎ 故OP＝OC·tan60°＝3 此时t＝4＋3 ‎∴t的值为4＋ 或4＋3 B A Q x P O y C D 图3‎ B A Q x P O y C D 图2‎ ‎（3）由题意知，若⊙P与四边形ABCD的边相切，有以下三种情况：‎ B A Q x P O y C D 图4‎ ‎①当⊙P与BC相切于点C时，有∠BCP＝90°‎ 从而∠OCP＝45°，得到OP＝3，此时t＝1‎ ‎②当⊙P与CD相切于点C时，有PC⊥CD 即点P与点O重合，此时t＝4‎ ‎③当⊙P与AD相切时，由题意，∠DAO＝90°‎ ‎∴点A为切点，如图4‎ PC 2＝PA 2＝( 9－t )2，PO 2＝( t－4 )2‎ 于是( 9－t )2＝( t－4 )2＋32，解得：t=5.6‎ ‎∴t的值为1或4或5.6‎ ‎31．（河北模拟）如图，在Rt△ABC中，∠C＝90°，AB＝10，AC＝6．点P从点A出发沿AB以每秒2个单位长的速度向点B匀速运动；点Q从点C出发沿CA以每秒1个单位长的速度向点A匀速运动．运动过程中DE保持垂直平分PQ，且交PQ于点D，交折线PB－BC于点E．点P、Q同时出发，当点P到达点B时停止运动，点Q也随之停止．设点P、Q运动的时间是t秒．‎ ‎（1）当t＝______________秒，直线DE经过点B；当t＝______________秒，直线DE经过点A；‎ ‎（2）四边形DPBE能否成为直角梯形？若能，求t的值；若不能，请说明理由；‎ ‎（3）当t为何值时，点E是BC的中点？‎ B Q A D C E P ‎（4）以E为圆心，EC长为半径的圆能否与AB、AC、PQ同时相切？若能，直接写出t的值；若不能，请说明理由．‎ B Q A D C P ‎(E)‎ 解：（1） ；2‎ 提示：在Rt△ABC中，∠C＝90°，AB＝10，AC＝6‎ ‎∴BC＝ ＝ ＝8‎ 当直线DE经过点B时，连接QB，则PB＝QB ‎∴(10－2t )2＝t 2＋8 2，解得t＝ （舍去）或t＝ B Q A D C P E 当直线DE经过点A时，AP＝AQ ‎∴2t＝6－t，即t＝2‎ ‎（2）①当DE∥PB时，四边形DPBE是直角梯形 此时∠APQ＝90°，由△AQP∽△ABC，得 ＝ B Q A D C P E 即 ＝ ，解得t＝ ‎②当PQ∥BC时，四边形DPBE是直角梯形 此时∠AQP＝90°，由△APQ∽△ABC，得 ＝ 即 ＝ ，解得t＝ B Q A D C P E ‎（3）连接QE、PE，作EG⊥PB于G，则QE＝PE ‎∵QE 2＝t 2＋4 2‎ PE 2＝PG 2＋EG 2＝(10－2t－ ×4)2＋( ×4)2‎ ‎∴t 2＋4 2＝(10－2t－ ×4)2＋( ×4)2‎ B Q A D C E P G 解得t＝ （舍去）或t＝ ‎（4）不能 设⊙E与AB相切于F点，连接EF、EP、EQ 则EC＝EF，EQ＝EP，∠ECQ＝∠EFP＝90°‎ ‎∴△ECQ≌△EFP，∴QC＝PF ‎∵∠C＝90°，∴⊙E与AC相切于C点 ‎∴AC＝AF，∴AQ＝AP 又AD＝AD，DQ＝DP ‎∴△ADQ≌△ADP，∴∠ADQ＝∠ADP＝90°‎ B Q A D C P E F 又∠QDE＝90°，∴A、D、E三点在同一直线上 由（1）知，此时t＝2，AQ＝6－t＝4‎ ‎∵AB＝10，AC＝6，∴sinB＝ ＝ ＝ 设EC＝EF＝x，则EB＝ ＝ x ‎∵EC＋EB＝BC，∴x＋ x＝8‎ ‎∴x＝3，∴EC＝EF＝3‎ ‎∴AE＝ ＝ ＝3 易知△ADQ∽△ACE，∴ ＝ ‎∴ ＝ ，∴AD＝ ‎∴ED＝AE－AD＝3－ ＝ ＝ 而EC＝3＝，∴ED＞EC ‎∴此时⊙E与PQ相离 ‎∴⊙E不能与AB、AC、PQ同时相切 ‎32．（山东青岛）如图，在Rt△ABC中，∠C＝90º，AC＝6cm，BC＝8cm，D、E分别是AC、AB的中点，连接DE．点P从点D出发，沿DE方向匀速运动，速度为1cm/s；同时，点Q从点B出发，沿BA方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（s）（0＜t ＜4）．解答下列问题：‎ ‎（1）当t为何值时，PQ⊥AB？‎ ‎（2）当点Q在B、E之间运动时，设五边形PQBCD的面积为y（cm2），求y与t之间的函数关系式；‎ ‎（3）在（2）的情况下，是否存在某一时刻t，使PQ分四边形BCDE两部分的面积之比为S△PQE : S五边形PQBCD ＝1 : 29？若存在，求出此时t的值以及点E到PQ的距离h；若不存在，请说明理由．‎ A P Q B C E D A B C 备用图 E D 解：（1）如图①，在Rt△ABC中，∠C＝90º，AC＝6，BC＝8‎ A P Q B C E D ‎①‎ ‎∴AB＝ ＝10‎ ‎∵D、E分别是AC、AB的中点 AD＝DC＝3，AE＝EB＝5，DE∥BC且DE＝ BC＝4‎ ‎∵PQ⊥AB，∴∠PQB＝∠C＝90°‎ 又∵DE∥BC，∴∠AED＝∠B ‎∴△PQE∽△ACB，∴ ＝ 由题意得：PE＝4－t，QE＝2t－5‎ ‎∴ ＝ ，解得t＝ A P Q B C E D ‎②‎ M ‎（2）如图②，过点P作PM⊥AB于M 由△PME∽△ACB，得 ＝ ‎∴ ＝ ，得PM＝ ( 4－t )‎ ‎∴S△PQE ＝ EQ·PM＝ ( 2t－5 )· ( 4－t )＝ t 2－ t＋6‎ S梯形DCBE ＝ ×( 4＋8 )×3＝18‎ ‎∴y＝18－( t 2－ t＋6)＝－ t 2＋ t＋12‎ ‎（3）假设存在时刻t，使S△PQE : S五边形PQBCD ＝1 : 29‎ 此时S△PQE ＝ S梯形DCBE ‎∴ t 2－ t＋6＝ ×18，解得t1＝2，t2＝ （舍去）‎ 当t＝2时，PM＝ ( 4－2 )＝ ，ME＝ ( 4－2 )＝ EQ＝5－2×2＝1，MQ＝ME＋EQ＝ ＋1＝ PQ＝＝ ‎∵ PQ·h＝ ，∴h＝ × ＝ ‎33．（山东烟台）如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4），以A为顶点的抛物线y＝ax 2＋bx＋c过点C．动点P从点A出发，沿线段AB向点B运动，同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位，运动时间为t秒．过点P作PE⊥AB交AC于点E．‎ ‎（1）直接写出点A的坐标，并求出抛物线的解析式；‎ ‎（2）过点E作EF⊥AD于F，交抛物线于点G．当t为何值时，△ACG的面积最大？最大值为多少？‎ x O y A D C B F G 图1‎ E 图1‎ P 图1‎ Q ‎（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．‎ x O y A D C B F G 图1‎ E 图1‎ P 图1‎ Q 解：（1）A（1，4）‎ 由题意，可设抛物线解析式为y＝a( x－1 )2＋4‎ ‎∵抛物线过点C（3，0）‎ ‎∴0＝a( 3－1 )2＋4，∴a＝－1‎ ‎∴抛物线的解析式为y＝－( x－1 )2＋4‎ 即y＝－x 2＋2x＋3‎ ‎（2）∵A（1，4），C（3，0）‎ ‎∴可求直线AC的解析式为y＝－2x＋6‎ P（1，4－t） 将y＝4－t代入y＝－2x＋6中，解得点E的横坐标为x＝1＋ ‎∴点G的横坐标为1＋ ，代入抛物线的解析式中，可求点G的纵坐标为4－ ‎∴GE＝( 4－ )－( 4－t )＝t－ 又点A到GE的距离为 ，C到GE的距离为2－ 即S△ACG ＝S△AEG ＋ S△CEG ＝ EG· ＋ EG( 2－ )＝ ·2( t－ )＝－ ( t－2 )2＋1‎ x O y A D C B E 图1‎ P 图1‎ Q H N 当t＝2时，S△ACG的最大值为1‎ ‎（3）t＝ 或t＝20－8 提示：∵A（1，4），C（3，0），∴AB＝4，BC＝2‎ ‎∴AC＝ ＝2，∴cos∠BAC＝ ＝ ＝ ‎∵PE⊥AB，AP＝t，∴AE＝ ＝ t ‎∴CE＝2－ t x O y A D C B E 图1‎ P 图1‎ Q H 若EQ＝CQ，则在矩形ABCD内存在点H，使四边形CQEH为菱形 过点Q作QN⊥EC于N，则CE＝2CN 在Rt△QNC中，CN＝CQ·cos∠ACD＝CQ·cos∠BAC＝ t ‎∴2－ t＝ t，解得t＝ 若CE＝CQ，则在矩形ABCD的AD边上存在点H，使四边形CQHE为菱形 ‎∴2－ t＝t，解得t＝20－8 ‎34．（山东模拟）把Rt△ABC和Rt△DEF按图1摆放（点C与点E重合），点B、C（E）、F在同一条直线上．∠BAC＝∠DEF＝90°，∠ABC＝45°，BC＝9，DE＝6，EF＝8．如图2，△DEF从图1的位置出发，以1个单位/秒的速度沿CB向△ABC匀速移动，在△DEF 移动的同时，点P从△DEF的顶点F出发，以3个单位/秒的速度沿FD向点D匀速移动．当点P移动到点D时，P点停止移动，△DEF也随之停止移动．DE与AC相交于点Q，连接BQ、PQ，设移动时间为t（s）．‎ ‎（1）设△BQE的面积为y，求y与t之间的函数关系式，并写出自变量t的取值范围；‎ ‎（2）当t为何值时，三角形DPQ为等腰三角形？‎ A B D E F 图2‎ P Q C ‎(E)‎ A B D C F 图1‎ ‎（3）是否存在某一时刻t，使P、Q、B三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由．‎ 解：（1）∵∠ACB＝45°，∠DEF＝90°，∴∠EQC＝45°‎ ‎∴EC＝EQ＝t，∴BE＝9－t A B D E F P Q C ‎∴y＝ BE·EQ＝ ( 9－t )t 即y＝－ t 2＋ t（0＜t ≤ ）‎ ‎（2）在Rt△DEF中，∵∠DEF＝90°，DE＝6，EF＝8‎ ‎∴DF＝ ＝ ＝10‎ ‎①当DQ＝DP时，则6－t＝10－3t，解得t＝2‎ A B D E F P Q C G ‎②当PQ＝PD时，过P作PG⊥DQ于G 则DH＝HQ＝ ( 6－t )‎ ‎∵HP∥EF，∴△DHP∽△DEF ‎∴ ＝ ，即 ＝ ，解得t＝ ‎③当QP＝QD时，过Q作QH⊥DP于H A B D E F H Q C P 则DH＝HP＝ ( 10－3t )‎ 可得△DHQ∽△DEF，∴ ＝ 即 ＝ ，解得t＝ ‎（3）假设存在某一时刻t，使P、Q、B三点在同一条直线上 A B D E F P Q C K 过P作PK⊥BF于K，则△PKF∽△DEF ‎∴ ＝ ＝ ，即 ＝ ＝ ‎∴PK＝ t，KF＝ t ‎∵P、Q、B三点共线，∴△BQE∽△BPK ‎∴ ＝ ，即 ＝ ，解得t＝ 即当t＝ 秒时，P、Q、B三点在同一条直线上 ‎35．（山东模拟）如图，在△ABC中，AB＝AC＝10cm，BD⊥AC于D，且BD＝8cm．点M从点A出发，沿AC方向匀速运动，速度为2cm/s；同时直线PQ由点B出发沿BA方向匀速运动，速度为1cm/s，运动过程中始终保持PQ∥AC，直线PQ交AB于P，交BC于Q，连接PM，设运动时间为t（s）．‎ ‎（1）当四边形PQCM是等腰梯形时，求t的值；‎ ‎（2）当点M在线段PC的垂直平分线上时，求t的值；‎ ‎（3）当t为何值时，①△PQM是等腰三角形；②△PQM是直角三角形；‎ ‎（4）是否存在时刻t，使以PM为直径的圆与BC相切？若存在，求出t的值；若不存在，请说明理由．‎ A C B D P Q M 解：（1）作PE⊥AC于E，作QF⊥AC于F E A C F B D P Q M 若四边形PQCM是等腰梯形，则ME＝CF 易知四边形PQFE是矩形，∴EF＝PQ ‎∵PQ∥AC，∴△PBQ∽△ABC ‎∵AB＝AC，∴PQ＝PB＝t，∴EF＝t ‎∵AB＝10，BD＝8，∴AD＝ ＝6‎ 易证△APE∽△ABD，∴ ＝ 即 ＝ ，∴AE＝6－ t ‎∴ME＝AE－AM＝6－ t－2 t＝6－ t CF＝AC－( AE＋EF )＝10－( 6－ t＋t )＝4－ t 由ME＝CF，得6－ t＝4－ t，解得t＝ A C B D P Q M G ‎∴当t＝ s时，四边形PQCM是等腰梯形 ‎（2）若点M在线段PC的垂直平分线上，则MP＝MC 作MG⊥AB于G，则△AMG∽△ABD ‎∴ ＝ ＝ ，∴ ＝ ＝ ‎∴AG＝ t，MG＝ t ‎∴PG＝10－t－ t＝10－ t 在Rt△GPM中，MP 2＝( t )2＋( 10－ t )2＝ t 2－44t＋100‎ 又∵MC 2＝( 10－2t )2＝4t 2－40t＋100‎ 由MP＝MC，得 t 2－44t＋100＝4t 2－40t＋100‎ 解得t1＝ ，t2＝0（舍去）‎ E A C B D P Q M ‎∴当t＝ s时，点M在线段PC的垂直平分线上 ‎（3）①若PQ＝PM，则t 2＝ t 2－44t＋100‎ 即8t 2－55t＋125＝0‎ ‎△＝(－55) 2－4×8×125＝－975＜0，方程无实数解 若MP＝MQ，则点M在线段PQ的垂直平分线上 作PE⊥AC于E，∴EM＝ PQ＝ t E A C B D P Q M F 由（1）知，AE＝6－ t ‎∵AE＋EM＝AM，∴6－ t＋ t＝2t 解得t＝ 若PQ＝MQ，作PE⊥AC于E，作QF⊥AC于F 由（1）知，QF＝PE ‎∵△APE∽△ABD，∴ ＝ 即 ＝ ，∴QF＝PE＝8－ t 又FM＝AM－( AE＋EF )＝2t－( 6－ t＋t )＝ t－6‎ ‎∴MQ 2＝(8－ t )2＋( t－6)2＝ t 2－32t＋100‎ 由PQ＝MQ，得t 2＝ t 2－32t＋100‎ 解得t1＝ ，t2＝10（舍去）‎ A C B D P Q M ‎∴当t＝ s或t＝ s时，△PQM是等腰三角形 ‎②若∠MPQ＝90°，则AM＝6－ t ‎∴2t＝6－ t，∴t＝ 若∠PMQ＝90°，则PM 2＋QM 2＝PQ 2‎ ‎∴ t 2－44t＋100＋ t 2－32t＋100＝t 2‎ 即12t 2－95t＋250＝0‎ E A C B D P Q M ‎△＝(－55) 2－4×8×125＝－2975＜0，方程无实数解 若∠PQM＝90°，作PE⊥AC于E 则AE＝6－ t，EM＝PQ＝t ‎∵AE＋EM＝AM，∴6－ t＋t＝2t ‎∴t＝ ‎∴当t＝ s或t＝ s时，△PQM是直角三角形 ‎（4）设PM的中点为N，分别过P、N、M作BC的垂线，垂足为G、K、H 易证△PBG∽△BCD，△MCH∽△BCD A C B D P Q M G H K N ‎∴ ＝ ， ＝ ‎∵AC＝10，AD＝6，∴DC＝4‎ ‎∴BC＝ ＝4 ‎∴ ＝ ， ＝ ‎∴PG＝ t，MH＝ (10－2t )‎ ‎∴NK＝ ( PG＋MH )＝ (10－t )‎ 若以PM为直径的圆与BC相切，则PM＝2NK ‎∴PM 2＝4NK 2‎ ‎∴ t 2－44t＋100＝ (10－t )2‎ 解得t1＝ ，t2＝ ‎∴当t＝ s或t＝ s时，以PM为直径的圆与BC相切 ‎36．（内蒙古包头、乌兰察布）如图，在Rt△ABC中，∠C＝90°，AC＝4cm，BC＝5cm，点D在BC上，且CD＝3cm．现有两个动点P、Q分别从点A和点B同时出发，其中点P以l cm/秒的速度沿AC向终点C运动；点Q以1.25 cm/秒的速度沿BC向终点C运动．过点P作PE∥BC交AD于点E，连接EQ．设动点运动时间为t秒（t＞0）．‎ ‎（1）连接DP，经过1秒后，四边形EQDP能够成为平行四边形吗？请说明理由；‎ ‎（2）连接PQ，在运动过程中，不论t取何值时，总有线段PQ与线段AB平行，为什么？‎ A D Q 图1‎ C P 图1‎ B 图1‎ E 图1‎ ‎（3）当t为何值时，△EDQ为直角三角形．‎ 解：（1）能．‎ ‎∵点P的速度为l cm/秒，点Q的速度为1.25 cm/秒，t＝1秒 A D Q 图1‎ C P 图1‎ B 图1‎ E 图1‎ ‎∴AP＝1，BQ＝1.25‎ ‎∴QD＝BC－CD－BQ＝5－3－1.25＝0.75‎ ‎∵PE∥BC，∴△APE∽△ACD ‎∴ ＝ ，即 ＝ ‎∴PE＝0.75，∴PE＝QD ‎∴四边形EQDP是平行四边形 ‎（2）∵AC＝4，BC＝5，AP＝t，BQ＝1.25t ‎∴CP＝4－t，CQ＝5－1.25t A D Q 图1‎ C P 图1‎ B 图1‎ E 图1‎ ‎∴ ＝ ， ＝ ＝ ‎∴ ＝ ，∴PQ∥AB ‎（3）①当∠EQD＝90°时 易证△EDQ∽△ADC，∴ ＝ 显然点Q在点D右侧，DQ＝1.25t－2，EQ＝PC＝4－t A D Q 图1‎ C P 图1‎ B 图1‎ E 图1‎ ‎∴ ＝ ，解得t＝2.5‎ ‎②当∠DEQ＝90°时 易证△DEQ∽△DCA，∴ ＝ ‎∵PE∥BC，∴△APE∽△ACD，∴ ＝ ‎∵AC＝4，CD＝3，∴AD＝5‎ ‎∴ ＝ ，∴AE＝1.25t，DE＝5－1.25t 显然点Q在点D右侧，DQ＝1.25t－2‎ ‎∴ ＝ ，解得t＝3.1‎ ‎∴当t＝2.5秒或t＝3.1秒时，△EDQ为直角三角形 ‎37．（内蒙古呼伦贝尔）如图①，在平面直角坐标系内，Rt△ABC≌Rt△FED，点C、D与原点O重合，点A、F在y轴上重合，∠B＝∠E＝30°，AC＝FD＝．△FED不动，△ABC沿直线BE以每秒1个单位的速度向右平移，直到点B与点E重合为止．设平移时间为x（秒），平移过程中AB与EF的交点为M．‎ ‎（1）求出图①中点B的坐标；‎ ‎（2）如图②，当x＝4秒时，求出过F、M、A三点的抛物线的解析式；此抛物线上有一动点P，以点P为圆心，以2为半径的⊙P在运动过程中是否存在与y轴相切的情况，若存在，直接写出P点的坐标；若不存在，请说明理由；‎ ‎（3）设移动x秒后两个三角形重叠部分的面积为S，求出整个运动过程中S与x的函数关系式．‎ F B D E O x y 图②‎ C A M A B C E ‎(F)‎ ‎(D)‎ O x y 图①‎ 解：（1）如图①，在Rt△ABC中，AC＝，∠B＝30°‎ A B C E ‎(F)‎ ‎(D)‎ O x y 图①‎ ‎∴BC＝AC＝3，∴B（－3，0）‎ ‎（2）如图②，∵x＝4，∴A（4，），B（1，0）‎ 过M作MH⊥BE于H 由题意，OE＝BC＝3，∴BE＝2‎ ‎∵∠B＝∠E，∴MB＝ME ‎∴BH＝ BE＝1，∴OH＝2，MH＝ ‎∴M（2，）‎ 设抛物线的解析式为y＝ax 2＋bx＋c，把F、M、A三点坐标代入 F B D E O x y 图②‎ C A M H 解得 ‎∴抛物线的解析式为y＝ x 2－ x＋ P1（2，）或P2（－2，3）‎ 提示：若半径为2的⊙P与y轴相切，那么点P的横坐标为2或－2‎ 当x＝2时，y＝ x 2－ x＋＝ 当x＝－2时，y＝ x 2－ x＋＝3 ‎∴存在符合条件的点P，坐标为P1（2，）或P2（－2，3）‎ ‎（3）当点B、O重合时，x＝3，所以整个运动过程可分为两个阶段：‎ ‎①当0≤x ＜3时，如图③‎ F B D E O x y 图③‎ C A M H G BO＝3－x，CD＝x，OG＝CH＝ BO＝ ( 3－x )‎ FG＝－ ( 3－x )＝ x ‎∴S＝S梯形FDCH － S△FGM ‎＝ [ ＋ ( 3－x )]·x－ ·x··x ‎＝－ x 2＋x F B D E O x y 图④‎ C A M ‎②当3≤x ≤6时，如图④，BE＝3－( x－3 )＝6－x ‎∴S＝S△BME ＝ ( 6－x )· ( 6－x )·＝ x 2－x＋3 综上所述，S与x的函数关系式为：‎ S＝ ‎38．（哈尔滨模拟）如图，在平面直角坐标系中，O为坐标原点，Rt△OAB的直角边OA在x轴正半轴上，且OA＝4，AB＝2，将△OAB沿某条直线翻折，使OA与y轴正半轴的OC重合．点B的对应点为点D，连接AD交OB于点E．‎ ‎（1）求AD所在直线的解析式：‎ ‎（2）连接BD，若动点M从点A出发，以每秒2个单位的速度沿射线AO运动，线段AM的垂直平分线交直线AD于点N，交直线BD于点Q．设线段QN的长为y（y≠0），点M的运动时间为t秒，求y与t之问的函数关系式（直接写出自变量t的取值范围）；‎ A O C x E B D y 备用图 A O C x E B D y ‎（3）在（2）的条件下，连接MN，当t为何值时，直线MN与过D、E、O三点的圆相切，并求出此时切点的坐标．‎ A O C x N B D y E Q H M 解：（1）由题意，△OAB≌△OCD ‎∴OC＝OA＝4，CD＝AB＝2‎ ‎∴D（2，4）‎ 设直线AD的解析式为y＝kx＋b，把A（4，0），D（2，4）代入 解得 ‎∴y＝－2x＋8‎ ‎（2）由B（4，2），D（2，4），可得直线BD的解析式为y＝－x＋6‎ ‎∵直线NQ垂直平分线段AM A O C x N B D y E Q H M ‎∴NH⊥AM，AH＝MH＝ AM＝ ×2t＝t ‎∴OH＝4－t，∴H（4－t，0）‎ ‎∴点Q、N的横坐标为为4－t ‎∴QH＝－( 4－t )＋6＝t＋2，NH＝－2( 4－t )＋8＝2t 当0＜t ＜2时，点Q在点N上方 y＝QN＝t＋2－2t＝－t＋2‎ 当t ＞2时，点Q在点N下方 y＝QN＝2t－( t＋2 )＝t－2‎ ‎（3）过点D作DF⊥OA于F，则CD∥OF，CD＝OF＝2‎ A O C x E B D y F K G I M O′M N ‎∵OA＝4，∴AF＝OF＝2‎ ‎∵DF⊥OA，∴OD＝AD，∠ODC＝∠DOF＝∠DAF ‎∵△OAB≌△OCD，∴∠COD＝∠AOB ‎∵∠COD＋∠AOD＝90°，∴∠OED＝∠AOB＋∠OAD＝90°‎ ‎∴OD为经过D、E、O三点的圆的直径，OD的中点O′ 为圆心 在Rt△OCD中，OD＝ ＝2 tan∠COD＝ ＝ ，tan∠ODC＝ ＝2‎ ‎∵NH垂直平分线段AM，∴∠NMA＝∠NAM ‎∵∠DOA＝∠NAM，∠NMA＝∠DOA，∴MN∥OD 设直线MN与⊙O′ 相切于G点，连接O′G，作GK⊥OA于K，MI⊥OD于I A O C x E B D y F K G I M O′M N 则∠OO′G＝∠O′GM＝90°‎ ‎∵MI⊥OD，∴四边形O′IMG为矩形 ‎∴IM＝O′G＝，MG＝O′I ‎∴OI＝ ，OM＝ ，∴MG＝O′I＝ ‎∴KG＝1，MK＝ ，∴OK＝3，∴G（3，1）‎ ‎∵OM＋AM＝OA，∴ ＋2t＝4，∴t＝ 同理可求当t＝ 时，切点G（－1，3）‎ ‎∴当t＝ 或t＝ 时，直线MN与过D、E、O三点的圆相切，切点分别为G（3，1）或G（－1，3）‎ ‎39．（哈尔滨模拟）如图，在平面直角坐标系中，直线y＝x＋b与x轴交于点A，与正比例函数y＝－ x的图象交于点B，过B点作BC⊥y轴，点C为垂足，C（0，8）．‎ ‎（1）求直线AB的解析式；‎ ‎（2）动点M从点A出发沿线段AO以每秒1个单位的速度向终点O匀速移动，过点M作x轴的垂线交折线A－B－O于点P．设M点移动的时间为t秒，线段BP的长为d，求d与t之间的函数关系式，并直接写出自变量t的取值范围；‎ ‎（3）在（2）的条件下，动点Q同时从原点O出发，以每秒1个单位的速度沿折线O－C－B向点B移动，当动点M停止移动时，点Q同时停止移动．当t为何值时，△BPQ是等腰三角形？‎ A O C B y x A O C B y x 备用图 A O C B y x 备用图 解：（1）∵BC⊥y轴，点C为垂足，C（0，8）‎ ‎∴点B的纵坐标为8‎ ‎∵y＝－ x，当y＝8时，x＝－6，∴B（－6，8）‎ A O C B y x P M D 把（－6，8）代入y＝x＋b，得8＝－6＋b，∴b＝14‎ ‎∴直线AB的解析式为y＝x＋14‎ ‎（2）由题意得AM＝t ‎∵直线AB：y＝x＋14交x轴于点A ‎∴A（－14，0），∴OA＝14‎ 过点B作BD⊥x轴于点D ‎∵B（－6，8），∴BD＝8，OD＝6‎ ‎∴AD＝14－6＝8，∴AB＝ ＝8 OB＝ ＝10，∴∠BAD＝45°，cos∠DOB＝ ‎①当点M在AD上时 A O C B y x P M D ‎∵PM⊥x轴，∴∠PMA＝90°，∴AP＝t ‎∴d＝BP＝AB－AP＝8－t（0≤t ＜8）‎ ‎②当点M在OD上时，OM＝14－t ‎∵∠PMO＝90°，cos∠DOB＝ ，∴OP＝ ( 14－t )‎ ‎∴d＝BP＝OB－OP＝10－ ( 14－t )＝ t－ （8＜t ≤14）‎ 综上，d＝ ‎（3）①当点P在AB上时（0≤t ＜8），Q在OC上 A O C B y x P M D Q BQ 2＝BC 2＋CQ 2＝6 2＋( 8－t )2‎ ‎∵PM＝OQ＝t，∠PMO＝∠MOQ＝90°‎ ‎∴四边形PMOQ为矩形，∴PQ＝OM＝14－t ‎∵PM＝OQ＝t，∴PQ∥AO ‎∴∠BPQ＝∠BAO＝∠ABD ‎∵∠PBQ＞∠ABD，∴∠PBQ＞∠BPQ，∴PQ≠BQ 当BP＝BQ时，( 8－t )2＝6 2＋( 8－t )2‎ A O C B y x P M D Q H 解得t1＝2或t2＝14‎ ‎∵0≤t ＜8，∴t2＝2‎ 当PB＝PQ时，( 8－t )2＝( 14－t )2，解得t＝2±6 ‎∵0≤t ＜8，∴t＝2±6 不合题意，舍去 ‎②当点P在BO上时（8＜t ≤14），Q在BC上 BQ＝6＋8－t＝14－t 当BP＝BQ时， t－ ＝14－t，解得t＝ A O C B y x P M D Q K 当PB＝PQ时，过点P作PH⊥BC于H ‎∴BQ＝2BH ‎∵BH＝DM＝t－8，∴14－t＝2( t－8 )，解得t＝10‎ 当QB＝QP时，过点Q作QK⊥BC于K ‎∴BP＝2BK ‎∵BP＝ ( t－8 )，BK＝ ( 14－t )‎ ‎∴( t－8 )＝ ( 14－t )，解得t＝ 综上，当t＝2或t＝10或t＝ 或t＝ 时，△BPQ是等腰三角形 ‎40．（哈尔滨模拟）如图，直线y＝ x＋12分别与x轴、y轴交于点A、B，直线BC交x轴于点C，且AB＝AC．‎ ‎（1）求直线BC的解析式；‎ ‎（2）点P从点C出发沿线段CO以每秒1个单位的速度向点O运动，过点P作y轴的平行线，分别交直线BC、直线AB于点Q、M，过点Q作QN⊥AB于点N．设点P的运动时间为t（秒），线段MN的长为d，求d与t的函数关系式，并直接写出自变量t的取值范围；‎ ‎（3）若经过A、N、Q三点的圆与直线BC交于另一点K，当t为何值时，KQ : AQ＝ : 10？‎ A O C N y x P Q B M K 解：（1）∵直线y＝ x＋12分别与x轴、y轴交于点A、B ‎∴A（－9，0），B（0，12），∴OA＝9，OB＝12‎ ‎∴AB＝ ＝15，∴sin∠BAO＝ ＝ ‎ ‎∵AB＝AC，∴AC＝15，∴C（6，0）‎ 设直线BC的解析式为y＝kx＋b ‎∴ 解得 ‎∴直线BC的解析式为y＝－2x＋12‎ ‎（2）由题意，PC＝t，∴OP＝6－t A O C N y x P Q B M K ‎∴点P的横坐标为6－t ‎∴PM＝ ( 6－t )＋12，PQ＝－2( 6－t )＋12‎ ‎∴MQ＝PM－PQ＝20－ t ‎∵∠AMP＋∠MAP＝∠AMP＋∠MQN＝90°‎ ‎∴∠MQN＝∠MAP＝∠BAO ‎∴sin∠MQN＝sin∠BAO＝ ‎∴MN＝MQ·sin∠MQN＝ ( 20－ t )＝16－ t ‎∴d＝16－ t（0≤t ＜6）‎ ‎（3）连接AK、AQ ‎∵∠ANQ＝90°，∴AQ为经过A、N、Q三点的圆的直径 ‎∴∠AKQ＝90°‎ ‎∵OB＝12，OC＝6，∴BC＝ ＝6 由S△ABC ＝ AC·OB＝ BC·AK，得AK＝6 ‎∵KQ : AQ＝ : 10，∴设KQ＝m，则AQ＝m 在Rt△AKQ中，AK 2＋KQ 2＝AQ 2‎ ‎∴( 6)2＋m 2＝( m )2，m＝2 ‎∴AQ＝m＝10 ‎∵tan∠BCO＝ ＝2，∴PQ＝PC·tan∠BCO＝2t 在Rt△AQP中，AP 2＋PQ 2＝AQ 2‎ ‎∴( 15－t )2＋( 2t )2＝( 10 )2‎ 解得t1＝1，t2＝5‎ ‎∴当t＝1或t＝5时，KQ : AQ＝ : 10‎ ‎41．（哈尔滨模拟）如图，直线y＝－kx＋6k（k ＞0）与x轴、y轴分别相交于点A、B，且△AOB的面积是24．‎ ‎（1）求直线AB的解析式；‎ ‎（2）点P从点O出发，以每秒2个单位的速度沿折线OA－AB运动；同时点E从点O出发，以每秒1个单位的速度沿y轴正半轴运动，过点E作与x轴平行的直线l，与线段AB相交于点F，当点P与点F重合时，点P、E均停止运动．连接PE、PF，设△PEF的面积为S，点P运动的时间为t秒，求S与t的函数关系式，并直接写出自变量t的取值范围；‎ B O y x E A F P l B O y x A 备用图 ‎（3）在（2）的条件下，过P作x轴的垂线，与直线l相交于点M，连接AM，当tan∠MAB＝ 时，求t的值．‎ 解：（1）∵y＝－kx＋6k，当x＝0时，y＝6k；当y＝0时，x＝6‎ ‎∴OA＝6，OB＝6k ‎∵S△AOB ＝24，∴×6×6k＝24，∴k＝ B O y x E A F P l H ‎∴直线AB的解析式为y＝－ x＋8‎ ‎（2）根据题意，OE＝t，EF∥OA，∴△BEF∽△BOA ‎∴ ＝ ，即 ＝ ，∴EF＝ ( 8－t )‎ ‎①当0＜t ≤3时，点P在OA上运动 过点P作PH⊥EF于H，则PH＝OE＝t ‎∴S＝ EF·PH＝ ·( 8－t )·t＝－ t 2＋3t ‎②当点P在AB上运动时 过点P作PG⊥OA于G，设直线PG与EF相交于点M，则MG＝OE＝t B O y x E A F P l G M 易知△APG∽△ABO，∴ ＝ ‎∵OA＝6，OB＝8，∴AB＝ ＝10‎ ‎∴ ＝ ，∴PG＝ ( 2t－6 )‎ 当点P与点F重合时，有PG＝OE ‎∴( 2t－6 )＝t，解得t＝8，即PG＝8‎ 点P与点F重合前，MP＝MG－PG＝t－ ( 2t－6 )＝－ t＋ ‎∴S＝ EF·MP＝ ·( 8－t )(－ t＋ )＝ t 2－ t＋ 综上，S＝ ‎（3）①当点P在OA上，点M在点F左侧时 B O y x E A F P l C M D 作MC⊥AB于C，FD⊥OA于D 则FD＝OE＝t，EM＝OP＝2t，MF＝EF－EM＝ ( 8－t )－2t 在Rt△CMF中， ＝tan∠MFC＝tan∠BAO＝ ＝ 设CM＝4k，则CF＝3k，MF＝ ＝5k 在Rt△MAC中， ＝tan∠MAC＝tan∠MAB＝ ‎∴AC＝2CM＝8k，∴AF＝5k，∴MF＝AF 在Rt△AFD中， ＝ ＝sin∠FAD＝sin∠BAO＝ ‎∴AF＝ t，∴( 8－t )－2t＝ t，解得t＝ 当点P在OA上，点M在点F右侧时，可求得t＝ B O y x E A F P l G M K ‎②当点P在AB上时，过点M作MK⊥AB于K 在Rt△PMK中， ＝tan∠MPK＝tan∠ABO＝ 设MK＝3m，则PK＝4m，MP＝5m，AK＝6m ‎∴AP＝AK－PK＝2m，∴2t－6＝2m ‎∵MP＝t－ ( 2t－6 )，∴t－ ( 2t－6 )＝5m ‎∴t－ ( 2t－6 )＝ ( 2t－6 )，解得t＝ 综上所述，满足条件的t值是 或 或 ‎42．（哈尔滨模拟）如图，在平面直角坐标系中，O为坐标原点，点A在x轴的正半轴上，△AOB为等腰三角形，且OA＝OB＝10，过点B作y轴的垂线，垂足为D，直线AB的解析式为y＝－3x＋30，点C在线段BD上，点D关于直线OC的对称点在腰OB上．‎ ‎（1）求点B坐标；‎ ‎（2）点P从点B出发，以每秒1个单位的速度沿折线BC－CO运动；同时点Q从点O出发，以每秒1个单位的速度沿对角线OB向终点B运动，当一点停止运动时，另一点也随之停止运动．设△PQC的面积为S，运动时间为t，求S与t的函数关系式，并写出自变量t的取值范围；‎ ‎（3）在（2）的条件下，连接PQ，设PQ与OB所成的锐角为α，当α＝90°－∠AOB时，求t的值．‎ C O y x D A B C O y x D A B 备用图 C O y x D A B F D′‎ 解：（1）过点B作BF⊥OA于F，设B（a，－3a＋30）‎ 在Rt△OBF中，a 2＋( －3a＋30 )2＝10 2‎ 解得a1＝10（舍去），a2＝8‎ 当a＝8时，－3a＋30＝6‎ ‎∴B（8，6） （2）设点D关于直线OC的对称点为D′，连接CD′‎ ‎∵D′ 在腰OB上，∴OD＝OD′，∠DOC＝∠D′OC 又OC＝OC，∴△DOC≌△D′OC ‎∴CD′＝CD，∠CDO′＝∠CDO＝90°‎ C O y x D A B E P Q ‎∴S△POQ ＝ OD·BD ＝ OD·CD ＋ OB·CD′‎ ‎∴CD＝ ＝ ＝3，∴BC＝5‎ ‎①当0≤t ＜5时，点P在线段BC上 过点Q作QE⊥BD于E，则△BQE∽△BOD ‎∴ ＝ ，即 ＝ ，∴QE＝6－ t ‎∴S＝ PC·QE＝ ( 5－t )( 6－ t )‎ C O y x D A B Q P F 即S＝ t 2－ t＋15‎ ‎②当5＜t ≤10时，点P在线段CO上 过点Q作QF⊥OC于F ‎∵COQ＝∠COD，∠QFO＝∠CDO＝90°‎ ‎∴△QFO∽△CDO，∴ ＝ 即 ＝ ，∴QF＝ t C O y x D A B P Q ‎∴S＝ PC·QF＝ ( t－5 )· t 即S＝ t 2－ t ‎（3）①当0≤t ＜5时 ‎∵α＝90°－∠AOB＝∠BOD，即∠PQB＝∠DOB ‎∴PQ∥DO，∴△BPQ∽△BDO ‎∴ ＝ ，即 ＝ ，∴t＝ ‎②当5＜t ≤10时，过点P作PH⊥OB于H C O y x D A B P Q H ‎∵∠PQO＝∠BOD，∴tan∠PQO＝∠BOD＝ 设PH＝4k，则QH＝3k，OH＝8k，OP＝4k ‎∴OQ＝11k，∴11k＝t，∴k＝ ‎ ‎∴OP＝4k＝ t 又∵OP＝3－( t－5 )＝3＋5－t ‎∴ t＝3＋5－t，∴t＝ ‎∴当α＝90°－∠AOB时，t的值为 或 ‎43．（哈尔滨模拟）如图，在平面直角坐标系中，点A（ ，0），点B（3，4），将△OAB沿直线OB翻折，点A落在第二象限内的点C处．‎ ‎（1）求点C的坐标；‎ ‎（2）动点P从点O出发，以每秒5个单位的速度沿OB向终点B运动，连接AP，将射线AP绕着点A逆时针旋转与y轴交于一点Q，且旋转角α＝ ∠OAB．设线段OQ的长为d，点P运动的时间为t秒，求d与t的函数关系式（直接写出时间t的取值范围）；‎ ‎（3）在（2）的条件下，连接CP．点P在运动的过程中，是否存在CP∥AQ，若存在，求此时t的值，并辨断点B与以点P为圆心，OQ长为半径的⊙P的位置关系；若不存在，请说明理由．‎ B O C x A y 备用图 B O C x A y 解：（1）过点B作BG⊥x轴于G，过点C作CH⊥x轴于H B O C x A y G H ‎∵A（ ，0），B（3，4），∴OA＝ ，OG＝3，BG＝4‎ ‎∴AG＝ ，∴AB＝ ＝ ，∴AB＝OA ‎∵△OAB沿直线OB翻折得到△OCB ‎∴△OAB≌△OCB，∴AB＝OA＝BC＝CO ‎∴四边形ABCO是菱形 ‎∴CO∥AB，∴∠COH＝∠BAG ‎∴Rt△CHO≌Rt△BGA，∴CH＝BG＝4，OH＝AG＝ B O C x A y E P Q ‎∴C（－ ，4） （2）连接AC交BO于点E ‎∵菱形ABCO，∴AC⊥BO，∠OAE＝ ∠OAB ‎∵α＝ ∠OAB，∴∠OAP＝∠OAE，∴∠OAQ＝∠EAP ‎∵∠AOQ＝∠AEP＝90°，∴△AOQ≌△AEP ‎∴ ＝ 由（1）知，CH＝4，AH＝ ‎∴AC＝ ＝ ，∴AE＝ ，同理OE＝ ‎①当0≤t ＜ 时 ‎∵OP＝5t，∴PE＝ －5t，∴ ＝ ‎∴d＝－ t＋ ‎②当 ＜t ≤1时，同理可求d＝ t－ B O C x A y E P Q F K ‎（3）过点P作PK⊥AB于K ‎∵AQ∥CP，∴∠PCE＝∠QAE ‎∵AE＝CE，AC⊥BO，∴PC＝PA ‎∴∠PAE＝∠PCE＝∠QAE＝ ∠PAQ ‎∴∠PAB＝∠QAE，∴∠PAE＝∠PAB，∴PE＝PK ‎∵菱形ABCO，∴∠PBK＝∠OBF ‎∴sin∠PBK＝sin∠OBF＝ ＝ ＝ ‎∵OP＝5t，OB＝5，∴PE＝5t－ ，PB＝5－5t ‎∴ ＝ ，解得t＝ ‎∴存在CP∥AQ，此时t＝ ‎∵ ＜ ＜1，∴当t＝ 时，OQ＝d＝ t－ ＝ BP＝OB－OP＝5－5t＝ ‎∴BP＝OQ，即点B与圆心P的距离等于⊙P的半径，点B在⊙P上 ‎∴存在CP∥AQ，此时t＝ ，且点B在⊙P上 ‎44．（黑龙江大庆）已知等边△ABC的边长为3个单位，若点P由A出发，以每秒1个单位的速度在三角形的边上沿A→B→C→A方向运动，第一次回到点A处停止运动，设AP＝S，用t表示运动时间．‎ A C B ‎（1）当点P由B到C运动的过程中，用t表示S；‎ ‎（2）当t取何值时，S等于 （求出所有的t值）；‎ ‎（3）根据（2）中t的取值，直接写出在哪些时段AP＜ ？‎ 解：（1）当点P在BC上时，有3≤t ≤6‎ 作PM⊥AB，垂足为M 由PB＝t－3，∠B＝60°，得PM＝ ( t－3 )，BM＝ ( t－3 )‎ ‎∴AM＝3－ ( t－3 )‎ 于是S＝AP＝ ＝（3≤t ≤6）‎ ‎（2）当S＝ 时 ‎（i）当点P在AB上时，有t＝ ‎（ii）当点P在CA上时，有t＝9－ ‎（iii）当点P在BC上时，S＝＝ 解得t＝4或t＝5‎ 综上t＝ 或t＝9－ 或t＝4或t＝5‎ ‎（3）根据（2）可知0＜t ＜，4＜t ＜5，9－＜t ≤9‎ 这三个时间段内AP＜ ‎45．（黑龙江大兴安岭、鸡西、齐齐哈尔、黑河、七台河）如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x 2－7x＋12＝0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．‎ ‎（1）求A、B两点的坐标．‎ ‎（2）求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标．‎ ‎（3）当t＝2时，在坐标平面内找一点M，使以A、P、Q、M为顶点的四边形是平行四边形，求M点的坐标；‎ B Q x P O y A ‎（4）在P、Q运动过程中，在坐标平面内是否存在点N，使以A、P、Q、N为顶点的四边形是菱形？若存在，请直接写出N点的坐标；若不存在，请说明理由．‎ B Q x P O y A 图1‎ 解：（1）解方程x 2－7x＋12＝0，得x1＝3，x2＝4‎ ‎∵OA＜OB，∴OA＝3，OB＝4‎ ‎∴A（0，3），B（4，0）‎ ‎（2）由题意得，AP＝t，AQ＝5－2t 可分两种情况讨论：‎ ‎①当∠APQ＝∠AOB时，△APQ∽△AOB 如图1， ＝ ，解得t＝ B Q x P O y A 图2‎ ‎∴Q（ ，）‎ ‎②当∠AQP＝∠AOB时，△APQ∽△ABO 如图2， ＝ ，解得t＝ ‎∴Q（ ，）‎ ‎（3）当t＝2时，AP＝2，AQ＝5－2t＝1‎ ‎∴PO＝1，∴P（0，1），‎ B Q x P O y A 图3‎ M 点Q的横坐标为：1×cos∠ABO＝ ，纵坐标为：3－1×sin∠ABO＝ ‎∴Q（ ，）‎ 若AP是平行四边形的边，则MQ∥AP，MQ＝AP＝2，如图3、图4‎ ‎∴点M的横坐标为 ，纵坐标为： ＋2＝ 或 － 2＝ ‎∴M1（ ，），M2（ ，）‎ B Q x P O y A 图4‎ M 若AP是平行四边形的对角线，则△AMP≌PQA，如图5‎ ‎∵点Q的横坐标为 ，∴点M的横坐标为－ ‎∵点A的纵坐标比点Q的纵坐标大 ‎∴点M的纵坐标比点P的纵坐标大 即点M的纵坐标为：1＋ ＝ B Q x P O y A 图5‎ M ‎∴M3（－ ，）‎ ‎（4）存在．N1（ ，），N2（ ，），N3（－ ，）‎ 提示：有三种情况 若AP＝AQ，则在坐标平面内存在点N，‎ 使四边形APNQ是菱形，如图6‎ ‎∴t＝5－2t，解得t＝ ，∴AQ＝ B Q x P O y A 图6‎ N ‎∴Q（ ，2），∴N1（ ，）‎ 若AP＝PQ，则在坐标平面内存在点N，‎ 使四边形APQN是菱形，如图7‎ 由题意，P（0，3－t），Q（4－ t， t）‎ ‎∴PQ 2＝( 4－ t )2＋( 3－t－ t )2‎ ‎∴t 2＝( 4－ t )2＋( 3－t－ t )2，解得t＝ 或t＝ B Q x P O y A 图7‎ N 当t＝ 时，点Q与点A重合，不合题意，舍去 ‎∴t＝ ，∴Q（ ，）‎ ‎∴N2（ ，）‎ 若AQ＝PQ，则在坐标平面内存在点N，‎ 使四边形ANPQ是菱形，如图8‎ B Q x P O y A 图8‎ N O′‎ 连接NQ交AP于O′，则NQ⊥AP，AO′＝O′P ‎∴AP＝2AO′，∴t＝ ( 5－2t )‎ 解得t＝ ，∴Q（ ，）‎ ‎∴N3（－ ，）‎ ‎46．（吉林）如图，在△ABC中，∠A＝90°，AB＝2cm，AC＝4cm．动点P从点A出发，沿AB方向以1cm/s的速度向点B运动，动点Q从点B同时出发，沿BA方向以1cm/s的速度向点A运动．当点P到达点B时，P，Q两点同时停止运动．以AP为一边向上作正方形APDE，过点Q作QF∥BC，交AC于点F．设点P的运动时间为t s，正方形APDE和梯形BCFQ重合部分的面积为S cm2．‎ ‎（1）当t＝_________s时，点P与点Q重合；‎ ‎（2）当t＝_________s时，点D在QF上；‎ ‎（3）当点P在Q，B两点之间（不包括Q，B两点）时，求S与t之间的函数关系式．‎ B Q D P C A E F B C A ‎（备用图）‎ 解：（1）1‎ ‎（2） 提示：点D在QF上时 ‎∵QF∥BC，∠DPQ＝CAB＝90°‎ ‎∴△PQD∽△ABC，∴ ＝ 即 ＝ ，解得t＝ ‎（3）如图①，当点D在BC上时 B Q D P C A E 图①‎ ‎(F)‎ 由四边形APDE是正方形，得DP∥AC ‎∴△BDP∽△BCA，∴ ＝ ＝ ＝ ‎∴PB＝ DP＝ t 由AP＋PB＝AB，得t＋ t＝2，解得t＝ 此时点E与点F重合 当1＜t ≤ 时 解法1：‎ 如图②，设DE交FQ于点H，则重合部分为梯形DHQP PQ＝AP＋QB－AB＝t＋t－2＝2t－2‎ B Q D P C A E F 图②‎ G H 过点Q作QG⊥DE于点G，则DG＝PQ＝2t－2‎ 由△HGQ∽△BAC，得HG＝ ‎∴HD＝HG＋GD＝ t＋2t－2＝ t－2‎ ‎∴S＝ ( PQ＋HD )·DP＝ ( 2t－2＋ t－2 )·t＝ t 2－2t 解法2：‎ 如图②，设DE交FQ于点H 由△FAQ∽△CAB，得AF＝2AQ＝2( 2－t )＝4－2t ‎∴EF＝AF－AE＝4－2t－t＝4－3t 由△FEH∽△CAB，得EH＝ EF＝2－ t ‎∴S梯形AQHE ＝ ( AQ＋EH )·AE＝ ( 2－t＋2－ t )·t＝－ t 2＋2t ‎∴S＝S正方形APDE － S梯形AQHE ＝t 2－( － t 2＋2t )＝ t 2－2t 由题意，当t＝2时，点P到达点B B Q D P C A E 图③‎ F M N 当 ＜t ＜2时 如图③，设DE交BC于点M，DP交BC于点N 则重合部分为六边形EFQPNM 由△FAQ∽△CAB，得AF＝4－2t ‎∴S△FAQ ＝ AQ·AF＝ ( 2－t )( 4－2t )＝( 2－t )2‎ 由△NPB∽△CAB，得PN＝4－2t ‎∴DN＝DP－NP＝t－( 4－2t )＝3t－4‎ 由△DMN∽△ABC，得DM＝ ( 3t－4 )‎ ‎∴S△DMN ＝ DM·DN＝ ·( 3t－4 )( 3t－4 )＝ ( 3t－4 )2‎ ‎∴S＝S正方形APDE － S△DMN － S△FAQ ＝t 2－ ( 3t－4 )2－( 2－t )2＝－ t 2＋10t－8‎ 综上所述，S＝ ‎47．（吉林模拟）如图，梯形OABC中，OA在x轴上，CB∥OA，∠OAB＝90°，B（4，4），BC＝2．动点E从点O出发，以每秒1个单位的速度沿线段OA运动，到点A停止，过点E作ED⊥x轴交折线O－C－B于点D，以DE为一边向右作正方形DEFG．设运动时间为t（秒），正方形DEFG与梯形OABC重叠面积为S（平方单位）．‎ ‎（1）求tan∠AOC的值；‎ ‎（2）求S与t的函数关系式，并求出S的最大值；‎ ‎（3）连接AC，AC的中点为M，t为何值时，△DMG为等腰三角形？‎ D A B C G O E F x y D A B C G O E F x 备用图 y D A B C G O E F x H y D A B C G O E x ‎(F)‎ y 解：（1）过C作CD⊥x轴于H ‎∵B（4，4），BC＝2，∴OH＝2，CH＝4‎ ‎∴tan∠AOC＝ ＝ ＝2，‎ ‎（2）当点F与点A重合时，OE＝t，AE＝DE＝4－t ‎∴tan∠AOC＝ ＝ ＝2，解得t＝ 当0＜t ≤ 时，S＝DE 2＝( 2OE )2＝( 2t )2＝4t 2‎ D A B C G O E F x y D A B C G O E F x y 当 ≤t ≤2时，S＝DE·AE＝2t·( 4－t )＝－2t 2＋8t 当2≤t ≤4时，S＝4AE＝4( 4－t )＝－4t＋16‎ 当0＜t ≤ 时，t＝ 时，S最大＝ 当 ≤t ≤2时，t＝2时，S最大＝8‎ 当2≤t ≤4时，t＝2时，S最大＝8‎ 综上，t＝2时，S的最大值为8‎ D A B C G O E F x M y D A B C G O E F x M y ‎（3）t1＝ ，t2＝ ，t3＝2－1‎ 提示：由题意，A（4，0），C（2，4）‎ ‎∴M（3，2）‎ 当0＜t ≤2时，D（t，2t），G（3t，2t）‎ ‎∴DM 2＝( t－3 )2＋( 2t－2 )2，DG 2＝4t 2‎ MG 2＝( 3t－3 )2＋( 2t－2 )2‎ 若DG＝MG，则4t 2＝( 3t－3 )2＋( 2t－2 )2‎ 解得t＝ ＞2（舍去）或t＝ 若MD＝MG，则( t－3 )2＋( 2t－2 )2＝( 3t－3 )2＋( 2t－2 )2‎ 解得t＝0（舍去）或t＝ D A B C G O E F x M 若DM＝DG，则( t－3 )2＋( 2t－2 )2＝4t 2，无实数解 当2＜t ≤4时，D（t，4），G（t＋4，4）‎ ‎∴DM 2＝( t－3 )2＋ 2 2，DG 2＝4 2‎ MG 2＝( t＋1 )2＋ 2 2‎ 若DG＝MG，则4 2＝( t＋1 )2＋ 2 2‎ 解得t＝2－1或t＝－2－1（舍去）‎ 若MD＝MG，则( t－3 )2＋ 2 2＝( t＋1 )2＋ 2 2‎ 解得t＝1（舍去）‎ 若DM＝DG，则( t－3 )2＋ 2 2＝4 2‎ 解得t＝3±2（舍去）‎ ‎48．（吉林长春）如图，在Rt△ABC中，∠ACB＝90°，AC＝8cm，BC＝4cm．D、E分别为边AB、BC的中点，连接DE．点P从点A出发，沿折线AD－DE－EB运动，到点B停止．点P在线段AD上以 cm/s的速度运动，在折线DE－EB上以1cm/s的速度运动．当点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M落在线段AQ上．设点P的运动时间为t（s）．‎ ‎（1）当点P在线段DE上运动时，线段DP的长为______________cm（用含t的代数式表示）．‎ ‎（2）当点N落在AB边上时，求t的值．‎ ‎（3）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S（cm2），求S与t的函数关系式．‎ ‎（4）连接CD．当点N与点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s的速度沿M－N－M连续做往返运动，直至点P与点E重合时，点H停止往返运动；当点P在线段EB上运动时，点H始终在线段MN的中心处．直接写出在点P的整个运动过程中，点H落在线段CD上时t的取值范围．‎ M C A B Q P N D E ‎（1）( t－2 )‎ M C A B Q P D E 图①‎ ‎(N)‎ ‎（2）①当点P在线段DE上时，如图①‎ PD＝PN＝PQ＝2，∴t－2＝2‎ ‎∴t＝4‎ ‎②当点P在线段EB上时，如图②‎ PN＝2PB ‎∵PN＝PC＝( t－6 )＋2＝t－4‎ M C A B N D E 图②‎ P ‎(Q)‎ PB＝2－( t－6 )＝8－t ‎∴t－4＝2( 8－t )，解得t＝ ‎∴当点N落在AB边上时，t的值为4或 ‎（3）①当2＜t ＜4时，如图③‎ M C A B N D E 图③‎ P Q S＝2 2－ ( 4－t )2‎ 即S＝－ t 2＋2t ‎②当 ＜t ＜8时，如图④‎ S＝( t－4 )2－ ( 3t－20 )2‎ M C A B N D E 图④‎ P ‎(Q)‎ 即S＝－ t 2＋22t－84‎ ‎（4）t＝ 或t＝5或6≤t ≤8‎ 提示：当点H第一次落在线段CD上时 ‎2.5( t－4 )＋ ( t－4 )＝2，解得t＝ 当点H第二次落在线段CD上时 ‎2.5( t－4 )－2＝ ( t－4 )，解得t＝5‎ 当点H第三次落在线段CD上时 ‎6－2.5( t－4 )＝ ( t－4 )，解得t＝6‎ 当6≤t ≤8时，点H恒在线段CD上 P A B C M O F D E N Q ‎49．（长春模拟）如图，在△AOB中，∠AOB＝90°，OA＝OB＝6，C为OB上一点，射线CD⊥OB交AB于点D，OC＝2．点P从点A出发以每秒 个单位长度的速度沿AB方向运动，点Q从点C出发以每秒2个单位长度的速度沿CD方向运动，P，Q两点同时出发，当点P到达点B时停止运动，点Q也随之停止．过点P作PE⊥OA于点E，PF⊥OB于点F，得到矩形PEOF，以点Q为直角顶点向下作等腰直角三角形QMN，斜边MN∥OB，且MN＝QC．设运动时间为t（秒）．‎ ‎（1）求t＝1时FC的长度．‎ ‎（2）求MN＝PF时t的值．‎ ‎（3）当△QMN和矩形PEOF有重叠部分时，求重叠（阴影）部分图形 面积S与t的函数关系式．‎ ‎（4）直接写出△QMN和矩形PEOF的边有三个公共点时t的值．‎ 解：（1）根据题意，△AOB、△AEP都是等腰直角三角形 P A C M O F D E N Q B 图①‎ G H ‎∵AP＝t，∴OF＝EP＝t ‎∵OC＝2，∴FC＝|2－t |‎ ‎∴当t＝1时，FC＝1‎ ‎（2）∵AP＝t，∴AE＝t，PF＝OE＝6－t ‎∵MN＝QC＝2t，MN＝PF ‎∴2t＝6－t，∴t＝2‎ ‎（3）当点F在点C左侧时，设MQ、MN分别与PF交于点G、H 当△QMN和矩形PEOF有重叠部分时 P A F M O C D E N Q B 图③‎ I J K L P A C M O F D E N Q B 图②‎ K 则MH＝GH＝t－( 2－t )＝2t－2≥0，得t ≥1‎ 当点F与点C重合时，t＝2‎ 当1≤t ≤2时，重叠部分为△MGH，如图①‎ ‎∵MH＝GH＝t－( 2－t )＝2t－2‎ ‎∴S ＝ ( 2t－2 )2＝2t 2－4t＋2‎ 当点E落在MQ上时，如图②‎ ‎∵AE＝t，EK＝MK＝t－2，AK＝6－t，AE＋EK＝AK ‎∴t＋( t－2 )＝6－t，∴t＝ P A F M O C D E N Q B 图④‎ K L 当2＜t ≤ 时，重叠部分为五边形IJKLP，如图③‎ ‎∵JK＝MK＝t－2，AK＝6－t，∴AJ＝6－t－( t－2 )＝8－2t ‎∴EK＝6－t－t＝6－2t，EI＝EJ＝8－2t－t＝8－3t ‎∴S ＝S矩形EKLP － S△EJI＝t( 6－2t )－ ( 8－3t )2＝－ t 2＋30t－32‎ A C M O D E N Q B 图⑤‎ ‎(F)‎ ‎(P)‎ ‎(F)‎ 当MN与EP重合时，t＝3‎ 当 ＜t ≤3时，重叠部分为矩形EKLP，如图④‎ ‎∴S ＝t( 6－2t )＝－2t 2＋6t ‎（4）t＝2或t＝ 提示：如图⑤、图②‎ A B R x E C Q D P M O y ‎50．（长春模拟）如图，在平面直角坐标系中，梯形ABCD的顶点A、B、D的坐标分别为A（－3，0），B（15，0），D（0，4），且CD＝10．一条抛物线经过C、D两点，其顶点M在x轴上．点P从点A出发以每秒5个单位的速度沿AD向点D运动，到点D后又以每秒3‎ 个单位的速度沿DC向点C运动，到点C停止；同时，点E从点B出发以每秒5个单位的速度沿BO运动，到点O停止．过点E作y轴的平行线，交边BC或CD于点Q，交抛物线于点R．设P、E两点运动的时间为t（秒）．‎ ‎（1）写出点M的坐标，并求这条抛物线的解析式；‎ ‎（2）当点Q和点R之间的距离为8时，求t的值；‎ ‎（3）直接写出使△MPQ成为直角三角形时t值的个数；‎ ‎（4）设P、Q两点直径的距离为d，当2≤d≤7时，求t的取值范围．‎ 解：（1）M（5，0）‎ A B R x E C Q D P M O y N 设抛物线的解析式为y＝a( x－5)2‎ ‎∵抛物线经过点D（0，4），∴25a＝4，∴a＝ ‎∴抛物线的解析式为y＝ ( x－5 )2或y＝ x 2－ x＋4‎ ‎（2）作CN⊥AB于N，则CN＝4，BN＝5‎ ‎①当0≤t ≤1时，由△BQE∽△BCN得： ＝ ＝ ‎∵BE＝5t，∴QE＝4t ‎∵RQ＝8，∴RE＝4t＋8‎ ‎∴R（15－5t，4t＋8）‎ ‎∵点R在抛物线y＝ ( x－5 )2上，∴( 15－5t－5 )2＝4t＋8‎ 解得t1＝ ＞1（舍去） ，t2＝ ‎②当1≤t ≤3时，QR≤CN＝4‎ ‎∴当t＝ 时，点Q和点R之间的距离为8‎ ‎（3）4‎ 提示：‎ 当0≤t ≤1时，P在线段AD上，Q在线段BC上，∠PMQ ≥∠DMC ＞90°‎ 当1＜t ≤ 时（P到达C时，t＝1＋ ＝），P、Q均在CD上 若∠PMQ＝90°，则由射影定理得：(8－3t )(10－5t )＝4 2‎ 解得t1＝ ，t2＝ 若∠PQM＝90°，则Q到达M的正上方，t＝ ＝2‎ 若∠QPM＝90°，则P到达M的正上方，t＝1＋ ＝ 所以使△MPQ成为直角三角形时的t值有4个 ‎（4）∵当t＝1时，P、Q分别到达D、C两点，CD＝10‎ ‎∴当2≤d ≤7时，P、Q均在CD上 当点P和点Q相遇前，d＝PQ＝3＋15－( 3t＋5t )＝18－8t ‎∴2≤18－8t ≤7，解得 ≤t ≤2‎ 当点P和点Q相遇后，d＝PQ＝8t－18‎ ‎∴2≤8t－18≤7，解得 ≤t ≤ ‎∵ ＞3，而3t－3＝7时，t＝ ‎∴≤t ≤ 综上所述，当2≤d ≤7时，t的取值范围为 ≤t ≤2或 ≤t ≤ ‎51．（辽宁大连）如图，△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，点P、Q同时从点C出发，以1cm/s的速度分别沿CA、CB匀速运动，当点Q到达点B时，点P、Q同时停止运动．过点P作AC的垂线l交AB于点R，连接PQ、RQ，并作△PQR关于直线l对称的图形，得到△PQ′R．设点Q的运动时间为t（s），△PQ′R与△PAR重叠部分的面积为S（cm2）．‎ ‎（1）t为何值时，点Q′ 恰好落在AB上？‎ ‎（2）求S与t的函数关系式，并写出t的取值范围；‎ B l A C Q P R Q′‎ ‎（3）S能否为 cm2？若能，求出此时的t值，若不能，说明理由．‎ B A 备用图 C B A 备用图 C 解：（1）过点Q′ 作Q′H⊥AC，垂足为H（如图1）‎ B l A C Q P R Q′‎ 图1‎ H ‎∴∠Q′HA＝90°＝∠C，Q′H∥BC ‎∴AQ′H△∽△ABC，∴ ＝ 由题意知QC＝CP＝PH＝Q′H＝t ‎∴ ＝ ，即AH＝ t ‎∵CP＋PH＋HA＝CA，即t＋t＋ t＝8‎ ‎∴t＝ ，即t为 s时，点Q′ 恰好落在AB上 B l A C Q P R Q′‎ 图2‎ ‎（2）①当0＜t ≤ 时（如图2）‎ 同理 ＝ ，即 ＝ ‎∴RP＝ ( 8－t )‎ ‎∴S＝S△PQ′R ＝S△PQR ＝ RP·CP＝ ×( 8－t )×t＝－ t 2＋3t ‎②当 ＜t ≤6时（如图3）‎ B l A C Q P R Q′‎ 图3‎ M H 设PQ′ 与AB相交于点M，过点M作MH⊥AC，垂足为H 设MH＝a，由对称性知，∠MPH＝∠QPC＝45°，则PH＝MH＝a 同理 ＝ ，即 ＝ ，∴AH＝ a ‎∵CP＋PH＋HA＝CA，即t＋a＋ a＝8‎ ‎∴a＝ ( 8－t )‎ ‎∴S＝ RP·PH＝ ×( 8－t )×( 8－t )＝ ( 8－t )2＝－ t 2－ t＋ 综上，S＝ ‎（3）若S＝ ，则 ‎①当0＜t ≤ 时，－ t 2＋3t＝ ，解得t1＝4＋（舍去），t2＝4－ ‎②当 ＜t ≤6时，( 8－t )2＝ ，解得t1＝8＋（舍去），t2＝8－ 即S能为 cm2，此时t为( 4－ )s或( 8－ )s