2009年福建省龙岩市初中毕业、升学考试试题及答案 9页

‎2009年龙岩市初中毕业、升学考试 考室座位号 数 学 试 题 ‎（满分：150分 考试时间：120分钟）‎ 注意：‎ 请把所有答案填涂或书写到答题卡上！请不要错位、越界答题！‎ 在本试题上答题无效。‎ 一、选择题（本大题共8小题，每小题3分，共24分。每小题的四个选项中，只有一个符合题意，请将正确的选项填涂到答题卡上）‎ ‎1．－2的相反数是 ‎ A．－2 B．‎2 ‎C． D．－‎ ‎2．下列运算正确的是 ‎ A．x2 + x3 = x5 B．(－ x2 )3 = x‎6 ‎C．x6÷x2 = x3 D．－2x·x2 =－2x3‎ ‎3．下列标志既是轴对称图形又是中心对称图形的是 ‎ A． B． C． D．‎ ‎4．如图所示几何体的左视图是 A． B． C． D．‎ ‎5．在同一直角坐标系中，函数与图象的交点个数为 ‎ A．3 B．‎2 ‎C．1 D．0‎ ‎6．计算的结果为 ‎ A．1 B．‎2 ‎C．－1 D．－2‎ ‎7．为了从甲、乙、丙、丁四位同学中选派两位选手参加数学竞赛，老师对他们的五次数学测验成绩进行统计，得出他们的平均分均为85分，且、、、. 根据统计结果，派去参加竞赛的两位同学是 ‎ A．甲、乙 B．甲、丙 C．甲、丁 D．乙、丙 ‎8．将一副三角板按图中方式叠放，则角α等于 ‎ A．30° B．45°‎ ‎ C．60° D．75°‎ 二、填空题（本大题共10小题，每小题3分，共30分。请将答案填入答题卡相应位置）‎ ‎9．分解因式：x2－4= .‎ ‎10．为减少全球金融危机对我国经济产生的影响，国务院决定拿出40000亿元以扩大内需，保持经济平稳较大增长. 这个数用科学记数法表示为 亿元.‎ ‎11．函数中自变量x的取值范围是 .‎ ‎12．如图，在△ABC中，点D、E、F分别是AB、AC、BC的中点，若△ABC的周长为‎12cm，则△DEF的周长是 cm.‎ ‎13．如图，点B、E、F、C在同一直线上. 已知∠A =∠D，∠B =∠C，要使 ‎△ABF≌△DCE，需要补充的一个条件是 (写出一个即可）.‎ ‎14．方程的解是 .‎ ‎15．小亮测得一圆锥模型的底面半径为‎5cm，母线长为‎7cm，那么它的侧面展开图的面积是 cm2（结果保留三个有效数字）.‎ ‎16．观察下列一组数：，，，，…… ，它们是按一定规律排列的. 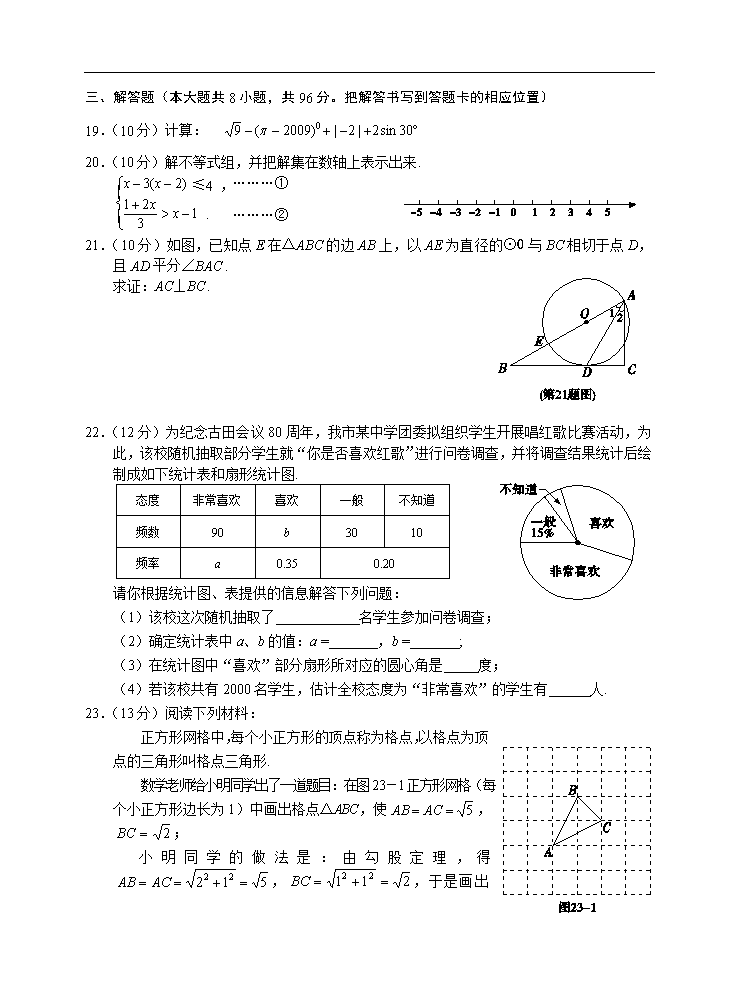那么这一组数的第k个数是 .‎ ‎17．在3 □ 2 □（－2）的两个空格□中，任意填上“+”或“－”，则运算结果为3的概率是 .‎ ‎18．如图，AB、CD是半径为5的⊙O的两条弦，AB = 8，CD = 6，‎ MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的 任意一点，则PA+PC的最小值为 .‎ ‎（背面还有试题）‎ ‎（背面还有试题）‎ 三、解答题（本大题共8小题，共96分。把解答书写到答题卡的相应位置）‎ ‎19．（10分）计算： ‎ ‎20．（10分）解不等式组，并把解集在数轴上表示出来.‎ ‎≤4 ，‎ ‎.‎ ‎………①‎ ‎………②‎ ‎ ‎ ‎21．（10分）如图，已知点E在△ABC的边AB上，以AE为直径的⊙O与BC相切于点D，且AD平分∠BAC .‎ 求证：AC⊥BC .‎ ‎22．（12分）为纪念古田会议80周年，我市某中学团委拟组织学生开展唱红歌比赛活动，为此，该校随机抽取部分学生就“你是否喜欢红歌”进行问卷调查，并将调查结果统计后绘制成如下统计表和扇形统计图.‎ 态度 非常喜欢 喜欢 一般 不知道 频数 ‎90‎ b ‎30‎ ‎10‎ 频率 a ‎0.35‎ ‎0.20‎ ‎ 请你根据统计图、表提供的信息解答下列问题：‎ ‎（1）该校这次随机抽取了 名学生参加问卷调查；‎ ‎（2）确定统计表中a、b的值：a = ，b = ;‎ ‎（3）在统计图中“喜欢”部分扇形所对应的圆心角是 度；‎ ‎（4）若该校共有2000名学生，估计全校态度为“非常喜欢”的学生有 人.‎ ‎23．（13分）阅读下列材料：‎ 正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫格点三角形.‎ ‎ 数学老师给小明同学出了一道题目：在图23－1正方形网格（每个小正方形边长为1）中画出格点△ABC，使，；‎ 小明同学的做法是：由勾股定理，得，，‎ 于是画出线段AB、AC、BC，从而画出格点△ABC.（1）请你参考小明同学的做法，在图23－2正方形网格（每个小正方形边长为1）中画出格点△（点位置如图所示），使==5，.（直接画出图形，不写过程）；‎ ‎· ·‎ ‎ （2）观察△ABC与△的形状，猜想∠BAC与∠‎ 有怎样的数量关系，并证明你的猜想.‎ ‎24．（13分）永定土楼是世界文化遗产“福建土楼”‎ 的组成部分，是闽西的旅游胜地. “永定土楼”‎ 模型深受游客喜爱. 图中折线（AB∥CD∥x轴）‎ 反映了某种规格土楼模型的单价y（元）与购买 数量x（个）之间的函数关系.‎ ‎ （1）求当10≤x≤20时，y与x的函数关系式；‎ ‎（2）已知某旅游团购买该种规格的土楼模型 总金额为2625元，问该旅游团共购买这种土楼模型多少个？(总金额=数量×单价)‎ ‎25．（14分）在边长为6的菱形ABCD中，动点M从点A出发，沿A→B→C向终点C运动，连接DM交AC于点N.‎ ‎（1）如图25－1，当点M在AB边上时，连接BN.‎ ‎①求证：△ABN≌△ADN；‎ ‎②若∠ABC = 60°，AM = 4，∠ABN =α，求点M到AD的距离及tanα的值；‎ ‎（2）如图25－2，若∠ABC = 90°，记点M运动所经过的路程为x（6≤x≤12）.‎ 试问：x为何值时，△ADN为等腰三角形.‎ ‎26．（14分）如图，抛物线与x轴交于A、B两点，与y轴交于C点，四边形OBHC为矩形，CH的延长线交抛物线于点D（5，2），连结BC、AD.‎ ‎（1）求C点的坐标及抛物线的解析式；‎ ‎（2）将△BCH绕点B按顺时针旋转90°后 再沿x轴对折得到 ‎△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；‎ ‎（3）设过点E的直线交AB边于点P，交CD边于点Q. 问是否存在点P，使直线PQ分梯形ABCD的面积为1∶3两部分？若存在，求出P点坐标；若不存在，请说明理由.‎ ‎2009年龙岩市初中毕业、升学考试 参 考 答 案 及 评 分 标 准 数 学 说明：评分最小单位为1分。若学生解答与本参考答案不同，参照给分。‎ 一、选择题（每小题3分，共24分）‎ ‎1．B 2．D 3．A 4．A 5．D 6．C 7．C 8．D 二、填空题（每小题3分，共30分。注：答案不正确、不完整均不给分）‎ ‎9．（x＋2）(x－2). 10．4 × 104 . 11．x ≤ 2. 12．6. ‎ ‎13．AB = DC（填AF=DE或BF=CE或BE=CF也对）.‎ ‎14．(只写也对). 15．110. 16．. 17．. 18．.‎ 三、解答题（共96分）‎ ‎19．（10分）解：原式= 3－1＋2＋2 × …………………………8分 ‎ = 5 …………………………………………10分 ‎20．（10分）解：由①，得x ≥ 1 …………………………………3分 ‎ 由②，得x < 4 …………………………………6分 ‎ ∴原不等式组的解集是：1 ≤ x < 4 ……………8分 ‎…… 10分 ‎21．（10分）证明：连接OD ……………………………1分 ‎ ∵OA = OD，∴∠1 =∠3； …………3分 ‎∵AD平分∠BAC，∴∠1 =∠2；‎ ‎∴∠2 =∠3；…………………………6分 ‎∴OD∥AC，…………………………7分 ‎∵BC是⊙O的切线 ‎∴OD⊥BC …………………………8分 ‎∴AC⊥BC ………………………10分 ‎22．（12分）（1）200；……………………………………3分 ‎（2）a = 0.45， b = 70 ……………………7分（每空2分）‎ ‎（3）126；……………………………………9分 ‎（4）900. ……………………………………12分 ‎23．（13分）（1）正确画出△（画出其中一种情形即可）6分 ‎ （2）猜想：∠BAC =∠ ………………8分 证明：∵，；‎ ‎∴， …………………………10分 ‎∴△ABC ∽ △，‎ ‎∴∠BAC =∠ ……………………………13分 ‎24．（13分）‎ 解：（1）当10 ≤ x ≤ 20时，设y = kx＋b（k≠0）……11分 ‎ 依题意，得 ………………………3分 ‎ 解得 ………………………………………5分 ‎∴当10 ≤ x ≤ 20时，y =－5x＋250 …………6分 ‎ （2）∵10 × 200 < 2625 < 20 × 150‎ ‎∴10 < x < 20 ………………………………………8分 依题意，得xy = x（－5x＋250）= 2625 …………10分 ‎ 即x2－50x＋525 = 0‎ 解得x1 = 15， x2 = 35（舍去）‎ ‎∴只取x = 15. ……………………………………12分 ‎ 答：该旅游团共购买这种土楼模型15个 …………13分 ‎25．（14分）‎ ‎（1）①证明：∵四边形ABCD是菱形 ‎ ∴AB = AD，∠1 =∠2 ………………………2分 ‎ 又∵AN = AN ‎ ∴△ABN ≌ △ADN ………………………4分 ‎ ②解：作MH⊥DA交DA的延长线于点H，由AD∥BC，得∠MAH =∠ABC = 60°，‎ ‎ 在Rt△AMH中，MH = AM·sin60° = 4×sin60° = 2， ‎ ‎ ∴点M到AD的距离为2. ………………………………………6分 易求AH=2，则DH=6＋2=8. ………………………………………7分 在Rt△DMH中，tan∠MDH=，‎ 由①知，∠MDH=∠ABN=α. ‎ 故tanα= …………………… 9分 ‎（2）解：∵∠ABC=90°，∴菱形ABCD是正方形 ‎ 此时，∠CAD=45°.‎ ‎ 下面分三种情形：‎ ‎ Ⅰ）若ND=NA，则∠ADN=∠NAD=45°.‎ ‎ 此时，点M恰好与点B重合，得x=6；……………10分 ‎ Ⅱ）若DN=DA，则∠DNA=∠DAN=45°.‎ ‎ 此时，点M恰好与点C重合，得x=12；………… 11分 ‎ Ⅲ）若AN=AD=6，则∠1=∠2，‎ 由AD∥BC，得∠1=∠4，又∠2=∠3，‎ ‎∴∠3=∠4，从而CM=CN，‎ 易求AC=6，∴CM=CN=AC－AN=6－6，‎ 故x = 12－CM=12－（6－6）=18－6 …………………………13分 综上所述：当x = 6或12 或18－6时，△ADN是等腰三角形 ………………… 14分 ‎（说明：对于Ⅰ）、Ⅱ）分类只要考生能写出x=6，x=12就给2分）‎ ‎26．（14分）‎ 解：（1）∵四边形OBHC为矩形，∴CD∥AB，‎ ‎ 又D（5，2），‎ ‎ ∴C（0，2），OC=2 . …………………………… 2分 ‎ ∴ 解得 ‎ ∴抛物线的解析式为： …… 4分 ‎ （2）点E落在抛物线上. 理由如下：……… 5分 ‎ 由y = 0，得. ‎ ‎ 解得x1=1，x2=4. ∴A（4，0），B（1，0）. ……………………………… 6分 ‎ ∴OA=4，OB=1.‎ ‎ 由矩形性质知：CH=OB=1，BH=OC=2，∠BHC=90°，‎ ‎ 由旋转、轴对称性质知：EF=1，BF=2，∠EFB=90°，‎ ‎ ∴点E的坐标为（3，－1）. ………………………………………………… 7分 ‎ 把x=3代入，得，‎ ‎ ∴点E在抛物线上. …………………………………………………………… 8分 ‎ （3）法一：存在点P（a，0），延长EF交CD于点G，易求OF=CG=3，PB=a－1.‎ ‎ S梯形BCGF = 5，S梯形ADGF = 3，记S梯形BCQP = S1，S梯形ADQP = S2，‎ ‎ ‎ 下面分两种情形：‎ ‎ ①当S1∶S2 =1∶3时，，‎ 此时点P在点F（3，0）的左侧，则PF = 3－a，‎ 由△EPF∽△EQG，得，则QG=9－‎3a，‎ ‎∴CQ=3－(9－‎3a) =‎3a －6‎ 由S1=2，得，解得；………………… 11分 ‎ ②当S1∶S2=3∶1时，‎ 此时点P在点F（3，0）的右侧，则PF = a－3，‎ 由△EPF∽△EQG，得QG = ‎3a－9，∴CQ = 3 +（‎3 a－9）= ‎3 a－6，‎ 由S1= 6，得，解得.‎ 综上所述：所求点P的坐标为（，0）或（，0）……… 14分 ‎ 法二：存在点P（a，0）. 记S梯形BCQP = S1，S梯形ADQP = S2，易求S梯形ABCD = 8.‎ 当PQ经过点F（3，0）时，易求S1=5，S2 = 3，‎ 此时S1∶S2不符合条件，故a≠3.‎ 设直线PQ的解析式为y = kx+b(k≠0)，则，解得，‎ ‎∴. 由y = 2得x = ‎3a－6，∴Q（‎3a－6，2） ……… 10分 ‎∴CQ = ‎3a－6，BP = a－1，.‎ 下面分两种情形：‎ ‎①当S1∶S2 = 1∶3时，= 2；‎ ‎ ∴‎4a－7 = 2，解得；……………………………………………… 12分 ‎②当S1∶S2 = 3∶1时，；‎ ‎ ∴‎4a－7 = 6，解得；‎ 综上所述：所求点P的坐标为（，0）或（，0）………… 14分 ‎[说明：对于第（3）小题，只要考生能求出或两个答案，就给6分. ]‎