2014四川广安中考数学试题 12页

‎2014年四川省广安市中考数学试卷 ‎（满分120分，考试时间120分钟）‎ 一、选择题（本大题共10个小题，每小题3分，共30分）‎ ‎1.（2014四川省广安市，1，3分）的相反数是（ ）‎ A． B． C．5 D．－5‎ ‎【答案】A ‎2. （2014四川省广安市，2，3分）下列运算正确的是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎3. （2014四川省广安市，3，3分）参加广安市2014年高中阶段教育学校招生考试的学生大约有4．3万人，将4．3万人用科学记数法表示应为（ ）‎ A．4．3×104人 B．43×103人 C．43×105人 D．4．3×105人 ‎【答案】A ‎4. （2014四川省广安市，4，3分）我市某校举办的行为规范在身边演讲比赛中，7位评委给其中一名选手的评分（单位：分）分别是：9．25，9．82，9．45，9．63，9．57，9．35，9．78，则这组数据的中位数和平均数分别是（ ）‎ A．9．63和9．54 B．9．57和9．55 C．9．63和9．56 D．9．57和9．57‎ ‎【答案】B ‎5. （2014四川省广安市，5，3分）要使二次根式在实数范围内有意义，则x的取值范围是（ ）‎ A． B． C．≥　　D．≤‎ ‎【答案】C ‎6. 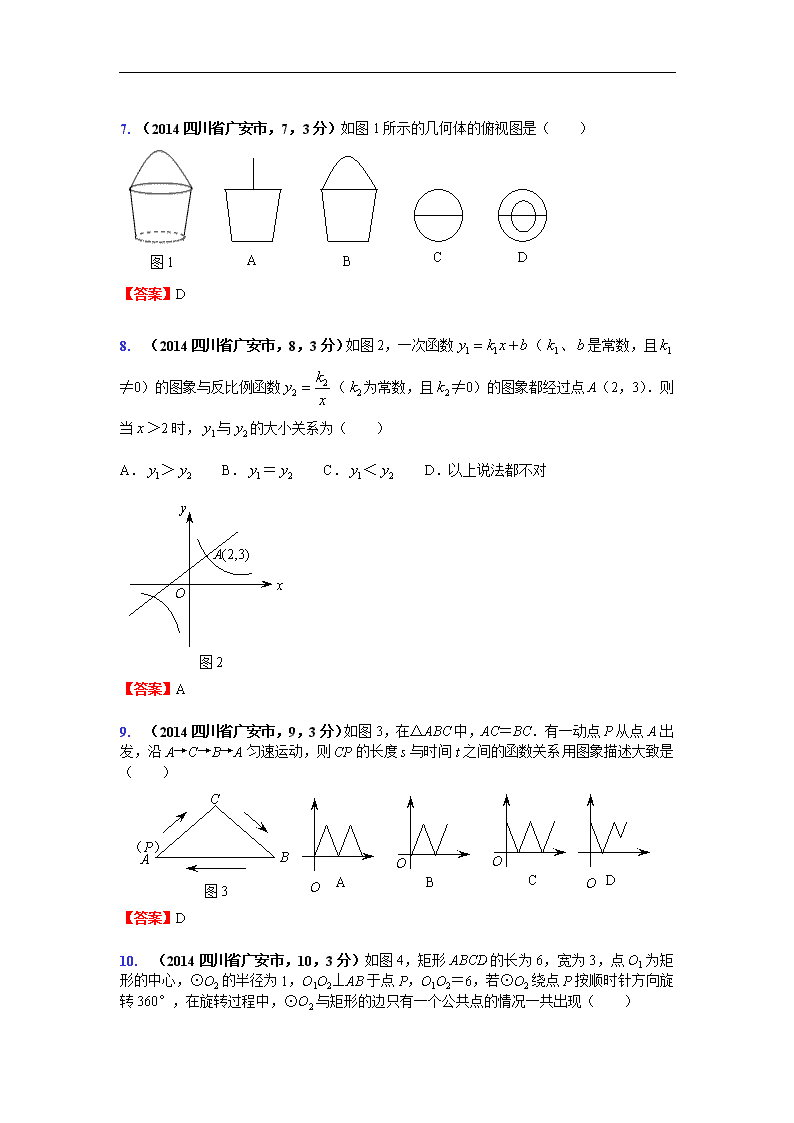（2014四川省广安市，6，3分）下列说法正确的是（ ）‎ A．为了了解全国中学生每天体育锻炼的时间，应采用普查的方式 B．若甲组数据的方差为0．03，乙组数据的方差是0．2，则乙组数据比甲组数据稳定 C．广安市明天一定会下雨 D．一组数据4，5，6，5，2，8的众数是5‎ ‎【答案】D ‎7. （2014四川省广安市，7，3分）如图1所示的几何体的俯视图是（ ）‎ 图1‎ A B C D ‎【答案】D ‎8. jscm（2014四川省广安市，8，3分）如图2，一次函数（、是常数，且≠0）的图象与反比例函数（为常数，且≠0）的图象都经过点A（2，3）．则当＞2时，与的大小关系为（ ）‎ A．＞ B．＝ C．＜ D．以上说法都不对 A(2,3)‎ x O y 图2‎ ‎【答案】A ‎9. jscm（2014四川省广安市，9，3分）如图3，在△ABC中，AC＝BC．有一动点P从点A出发，沿A→C→B→A匀速运动，则CP的长度s与时间t之间的函数关系用图象描述大致是（ ）‎ A ‎（P）‎ C B 图3‎ A D O B O C O O ‎【答案】D ‎10. jscm（2014四川省广安市，10，3分）如图4，矩形ABCD的长为6，宽为3，点O1为矩形的中心，⊙O2的半径为1，O1O2⊥AB于点P，O1O2＝6，若⊙O2绕点P按顺时针方向旋转360°，在旋转过程中，⊙O2与矩形的边只有一个公共点的情况一共出现（ ）‎ A．3次 B．4次 C．5次 D．6次 ‎ D ‎ ‎ A ‎ ‎ B ‎ ‎ C ‎ ‎ O1 ‎ ‎ O2 ‎ ‎ P ‎ 图4 ‎ ‎【答案】B 二、填空题（本大题共6小题，每小题3分，满分18分.）‎ ‎11.（2014四川省广安市，11，3分）直线沿轴向下平移5个单位，则平移后直线与轴的交点坐标为________．‎ ‎【答案】（0，－3）‎ ‎12. （2014四川省广安市，12，3分）分解因式：________． ‎ ‎【答案】‎ ‎13. （2014四川省广安市，13，3分）化简的结果是________． ‎ ‎【答案】‎ ‎14. （2014四川省广安市，14，3分）若∠α的补角为76°28′，则∠α＝________．‎ ‎【答案】103°32′‎ ‎15. （2014四川省广安市，15，3分）一个多边形的内角和比四边形内角和的3倍多180°，这个多边形的边数是________．‎ ‎【答案】9‎ ‎16. （2014四川省广安市，16，3分）如图5，在直角梯形ABCD中，∠ABC＝90°，上底AD为，以对角线BD为直径的⊙O与CD切于点D，与BC交于点E，∠ABD为30°，则图中阴影部分的面积为________．（不取近似值）‎ ‎【答案】‎ 三、解答题（本大题共4小题，第17题5分，第18、19、20题各6分）‎ ‎17. jscm（2014四川省广安市，17，5分）（5分）．‎ 解：原式＝‎ ‎＝3－1＝2．‎ ‎18.jscm（2014四川省广安市，18，6分）6分）解不等式组，并写出不等式组的整数解．‎ ‎【答案】解：‎ 解不等式①，得≤4；‎ 解不等式②，得＞2．‎ 所以这个不等式组的解集为2＜≤4．‎ 这个不等式组的整数解为3，4．‎ ‎19. （2014四川省广安市，19，6分）如图6，在正方形ABCD中，P是对角线AC上一点，连接BP、DP，延长BC到E，使PB＝PE．求证：∠PDC＝∠PEC．‎ A B C D P E 图6‎ ‎【答案】证明：在正方形ABCD中，BC＝DC，∠PCB＝∠PCD，‎ 又∵PC＝PC，‎ ‎∴△PCB≌△PCD（SAS）．‎ ‎∴∠PBC＝∠PDC．‎ ‎∵PB＝PE，‎ ‎∴∠PBC＝∠PEC．‎ ‎∴∠PDC＝∠PEC．‎ ‎20. （2014四川省广安市，20，6分）如图7，反比例函数（为常数，且≠0）经过点A（1，3）．‎ ‎（1）求反比例函数的解析式；‎ ‎（2）在轴正半轴上有一点B，若△AOB的面积为6，求直线AB的解析式．‎ A(1，3)‎ B O x y 图7‎ ‎【答案】解：（1）∵反比例函数的图象经过点（1，3），‎ ‎∴．解＝3．‎ ‎∴反比例函数的解析式是．‎ ‎（2）由题意，得．解得，即B（4，0）．‎ 设直线AB的解析式为，由于直线AB过点（1，3），（4，0），‎ ‎∴，解．‎ ‎∴直线AB的解析式为．‎ 四、实践应用（本大题共4个小题，第21题6分，第22、23、24小题各8分，共30分）‎ ‎21.（2014四川省广安市，21，6分）大课间活动时，有两个同学做了一个数字游戏：有三张正面写有数字－1，0，1的卡片，它们背面完全相同，将这三张卡片背面朝上洗匀后，其中一个同学随机抽取一张，将其正面的数字作为p的值；然后将卡片放回并洗匀，另一个同学再从这三张卡片中随机抽取一张，将其正面的数字作为q的值，两次结果记为（p，q）．‎ ‎（1）请你帮他们用树状图或列表法表示（p，q）所有可能出现的结果；‎ ‎（2）求满足关于x的方程＝0没有实数解的概率．‎ ‎【答案】解：解：（1）列表表示（p，q）所有可能的结果如下，共有9种：‎ p ‎（p，q） q ‎－1‎ ‎0‎ ‎1‎ ‎－1‎ ‎（－1，－1）‎ ‎（－1，0）‎ ‎（－1，1）‎ ‎0‎ ‎（0，－1）‎ ‎（0，0）‎ ‎（0，1）‎ ‎1‎ ‎（1，－1）‎ ‎（1，0）‎ ‎（1，1）‎ ‎（2）当时，方程没有实数解，满足的（p，q ‎）共有3对：（－1，1），（0，1），（1，1）．∴关于x的方程＝0没有实数解的概率是．‎ ‎22. jscm（2014四川省广安市，22，8分）广安某水果店计划购进甲、乙两种新出产的水果共140千克，这两种水果的进价、售价如下表所示：‎ 进价（元／千克）‎ 售价（元／千克）‎ 甲种 ‎5‎ ‎8‎ 乙种 ‎9‎ ‎13‎ ‎（1）若该水果店预计进货款为1000元，则这两种水果各购进多少千克？‎ ‎（2）若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍，应怎样安排进货才能使水果店在销售完这批水果时获利最多？此时利润为多少元？‎ ‎【答案】解：解：（1）设甲种水果购进千克，则乙种水果购进千克．由题意，得 ‎．‎ 解得＝65．140－＝75．‎ 答：甲、乙两种水果分别购进65千克、75千克．‎ ‎（2）设水果的销售利润为元，则 ‎＝＝－＋560．‎ ‎∵＝－1＜0，∴随的增大而减小．‎ 由题意，有≤，解得≥35．‎ ‎∴当＝35时，有最大值，此时＝－35＋560＝525（元）．‎ 答：购甲种水果35千克，乙种水果105千克时获利最多，此时利润为525元．‎ ‎23. （2014四川省广安市，23，8分）为邓小平诞辰110周年献礼，广安市政府对城市建设进行了整改．如图8，已知斜坡AB长60米，坡角（即∠BAC）为45°，BC⊥AC，现计划在斜坡中点D处挖去部分斜坡，修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE（下面两个小题结果都保留根号）．‎ ‎（1）若修建的斜坡BE的坡比为∶1，求休闲平台DE的长是多少米？‎ ‎（2）一座建筑物GH距离A点33米远（即AG＝33米），小亮在D点测得建筑物顶部H的仰角（即∠HDM）为30°．点B、C、A、G、H在同一个平面内，点 C、A、G在同一条直线上，且HG⊥CG，问建筑GH高为多少米？‎ B 图8‎ H F A D E P M G ‎45°‎ ‎30°‎ C ‎【答案】解：解：（1）∵BC⊥AC，∠BAC＝45°，‎ ‎∴△ABC为等腰直角三角形．‎ ‎∵DE∥AC，‎ ‎∴△BDF为等腰直角三角形．‎ ‎∵AB＝60，‎ ‎∴AC＝BC＝60．‎ ‎∵D这AB的中点，‎ ‎∴BD＝30．‎ ‎∴BF＝DF＝30．‎ ‎∵BE的坡比为∶1，‎ ‎∴∠BEF＝60°．‎ ‎∴EF＝＝＝10．‎ ‎∴DE＝30－EF＝30－10．‎ 答：休闲平台DE的长为（30－10）米．‎ ‎（2）过D作DP⊥AC于P，DM⊥GH于M，则四边形GPDM为矩形．‎ ‎∵D为AB的中点，‎ ‎∴AD＝AB＝30．‎ ‎∴AP＝DP＝GM＝30．‎ ‎∴MD＝GP＝33＋30＝＝63．‎ ‎∵，即，‎ ‎∴＝＝．‎ ‎∴GH＝GM＋HM＝（30＋）（米）．‎ 答：建筑物GH高为（30＋）米．‎ ‎24. （2014四川省广安市，24，8分）在校园文化建设活动中，需要裁剪一些菱形来美化教室．现有平行四边形ABCD的邻边长分别为1，（＞1）的纸片，先减去一个菱形，余下一个四边形，在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，…，依次类推，请画出剪3次后余下的四边形是菱形的裁剪线的各种示意图，并求出的值．‎ ‎【答案】解：解：如图（1），此时＝4．‎ 如图（2），此时＝2＋＝．‎ 如图（3），此时＝1＋＝．‎ 如图（4），此时＝1＋＝．‎ 图（2）‎ ‎1‎ 图（3）‎ ‎1‎ 图（1）‎ ‎1‎ 图（4）‎ ‎1‎ 五、推理与论证（9分）‎ ‎25. （2014四川省广安市，25，9分）如图9，AB为⊙O的直径，以AB为直角边作Rt△ABC，∠CAB＝90°，斜边BC与⊙O交于点D，过点D作⊙O的切线DE交AC于点E，DG⊥AB于F，交⊙O于点G．‎ ‎（1）求证：E是AC的中点；‎ ‎（2）若AE＝3，＝，求DG的长．‎ A G 图9‎ B C E D F O ‎【答案】解：解：（1）连接OD，AD．‎ A G 图9‎ B C E D F O ‎∵EA⊥AB，‎ ‎∴EA是⊙O的切线．‎ ‎∵DE是⊙O的切线，‎ ‎∴EA＝DE．‎ ‎∵AB是⊙O的直径，‎ ‎∴∠ADB＝90°．‎ ‎∴∠DAB＋∠DBA＝∠C＋∠DBA＝90°．‎ ‎∴∠DAB＝∠C．‎ ‎∵OA＝OD，‎ ‎∴∠DAB＝∠ADO．‎ 又∵∠ADO＋∠ADE＝∠ADE＋∠EDC＝90°，‎ ‎∴∠ADO＝∠EDC．‎ ‎∴∠DAB＝∠EDC．‎ ‎∴∠C＝∠EDC．‎ ‎∴DE＝CE．‎ ‎∴AE＝CE．‎ ‎∴E是AC的中点．‎ ‎（2）由（1）知，E是AC的中点，‎ ‎∴AC＝2AE＝6．‎ 在Rt△ABC中，＝，∴BC＝9．‎ 在Rt△ADC中，＝，∴CD＝4．‎ ‎∴BD＝9－4＝5．‎ 又∵DF⊥AB，CA⊥AB，‎ ‎∴AC∥DF，DF＝FG＝DG．‎ ‎∴∠FDB＝∠ACB．‎ 在Rt△DFB中，，‎ ‎∴DF＝．‎ ‎∴DG＝2DF＝．‎ 六、拓展探究（10分）‎ ‎26. （2014四川省广安市，26，10分）如图10，在平面直角坐标系中，抛物线与x轴交于点A（－4，0），B（－1，0）两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在第三象限的抛物线上有一动点D．‎ ‎①如图（1），若四边形ODAE是以OA为对角线的平行四边形，当平行四边形ODAE的面积为6时，请判断平行四边形ODAE是否为菱形？说明理由．‎ ‎②如图（2），直线与抛物线交于点Q、C两点，过点D作直线DF⊥x轴于点H，交QC于点F．请问是否存在这样的点D，使点D到直线CQ的距离与点C到直线DF的距离之比为∶2？若存在，请求出点D的坐标；若不存在，请说明理由．‎ y A B C D E O x y ‎（1）‎ A B C D Q O x ‎（2）‎ F H 图10‎ ‎【答案】解：解：（1）∵抛物线经过点A（－4，0），B（－1，0），‎ ‎∴，解得．‎ ‎∴抛物线的解析式是．‎ ‎（2）①如图（1），过D作DM⊥轴于M，设D点的坐标为（，），‎ ‎∵点D在抛物线上，‎ ‎∴．‎ 当平行四边形ODAE的面积是6时，△ADO的面积是3，‎ ‎∴OA·DM＝3，即×4×[－（）]＝3．解得＝－2，或＝－3．‎ 当＝－2时，M为OA的中点，由于DM⊥轴，‎ ‎∴DA＝DO．‎ ‎∴平行四边形ODAE为菱形．‎ 当＝－3时，AM≠OM，由勾股定理可求得，DA≠DO，‎ ‎∴平行四边形ODAE不是菱形．‎ A B C D E O x y ‎（1）‎ M y A B C D Q O x ‎（2）‎ F H P M ‎②如图（2），存在符合要求的点D．理由如下：‎ 作CP⊥DF于P，DM⊥CQ于M，设D（，）．‎ ‎∵F点的横坐标也是D点的横坐标，将x＝a代入，得，∴F（，）．‎ ‎∴DF＝．‎ ‎∵D点在抛物线上，‎ ‎∴，即DF＝（）．‎ 在中，令0，得3，∴C（0，3）．‎ ‎∴PF＝3－（）＝－．‎ 在Rt△CPF中，CF＝．‎ ‎∵∠DMF＝∠CPF＝90°，∠DFM＝∠CFP，‎ ‎∴△CPF∽△DMF．‎ 又∵，‎ ‎∴，‎ ‎∴．‎ 解得＝－．则＝－．‎ ‎∴D（－，－）．‎