2008年四川省自贡市初中毕业暨升学考试题及参考答案 13页

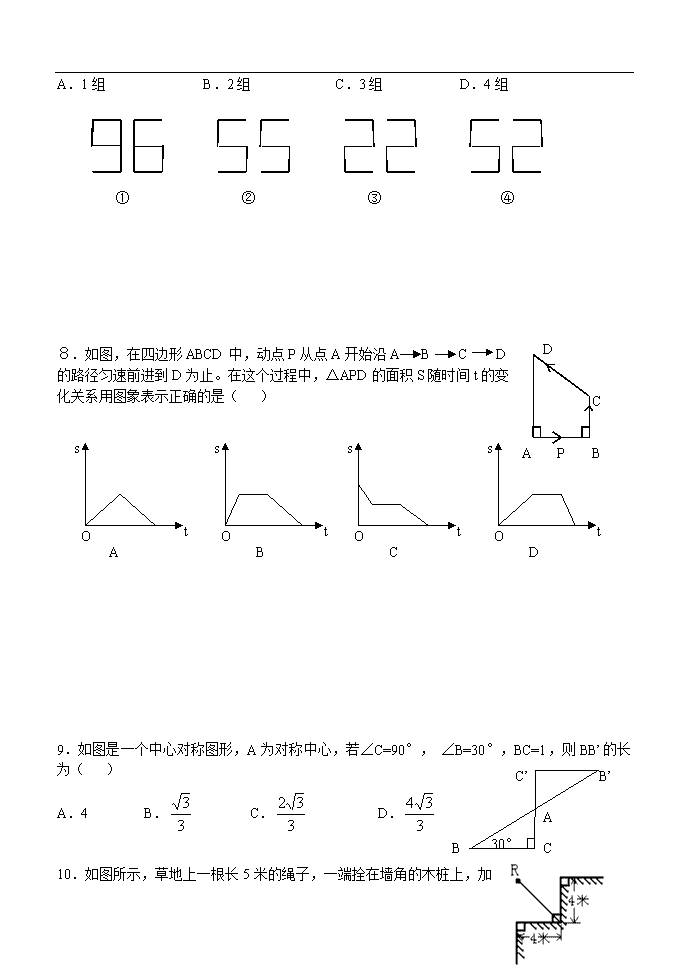
四川省自贡市2008年初中毕业暨升学考试 数学试卷 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分120分。考试时间120分。‎ 第Ⅰ卷（选择题 共30分）‎ 一、选择题 ：本大题共10个小题，每小题3分，共30分。每小题给出的四个选项中，只有一个选项是符合题目要求的。‎ ‎1．当时，的值为（ ）‎ A．4 B．－４　　　　 　C．２　　　　　 　D．－２‎ ‎２．方程的解的相反数是（ ）‎ A．2 B．－２ C．3 D．－3‎ ‎3．图中所示几何体的俯视图是 主视方向 A B C D ‎4．下面几组条件中，能判断一个四边形是平行四边形的是（ ）‎ A．一组对边相等 B．两条对角线互相平分 ‎ C．一组对边平行 D．两条对角线互相垂直 ‎5．元旦游园晚会上，有一个闯关活动：将20个大小重量完全要样的乒乓球放入一个袋中，其中8个白色的，5个黄色的，5个绿色的，2个红色的。如果任意摸出一个乒乓球是红色，就可以过关，那么一次过关的概率为（ ）‎ A． B． C． D．‎ ‎6．已知α为锐角，且cot（90°－α）＝，则α的度数为（ ）‎ A．30° B．60° C．45° D．75°‎ ‎7．如下所示的4组图形中，左边图形与右边图形成中心对称的有（ ）‎ A．1组 B．2组 C．3组 D．4组 ‎①‎ ‎②‎ ‎③‎ ‎④‎ D C B P A ‎８．如图，在四边形ABCD中，动点P从点A开始沿A B C D 的路径匀速前进到D为止。在这个过程中，△APD的面积S随时间t的变 化关系用图象表示正确的是（ ）‎ s t O A s t O B s t O C s t O D ‎30°‎ A C B’‎ B C’”””””‎ ‎9．如图是一个中心对称图形，A为对称中心，若∠C=90°， ∠B=30°，BC=1，则BB’的长为（ ）‎ A．4 B． C． D．‎ ‎10．如图所示，草地上一根长5米的绳子，一端拴在墙角的木桩上，加一端栓着一只小羊R。那么，小羊在草地上的最大活动区域的面积是（ ）‎ A． B． ‎ ‎ C． D．‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：本大题共5小题，每小题4分，共20分。‎ ‎11．北京奥运圣火于2008年3月25日在希腊奥林匹亚按照传统仪式取火，火炬接力时间为130天，传递总里程约13.7万公里。用科学记数法表示13.7万这个数为 。‎ ‎12．写出一个有理数和一个无理数，使它们都是小于－1的数 。‎ ‎13．如图矩形ABCD中，AB＝8㎝，CB＝4㎝，E是DC的中点，BF＝BC，则四边形DBFE的面积为 。‎ ‎14．往返于甲、乙两地的火车中途要停靠三个站，则有 种不同的票价（来回票价一样），需准备 种车票。‎ ‎15．如图，⊙O是△ABC的外接圆，⊙O的半径R＝2，sinB＝‎ ‎，则弦AC的长为 。‎ 三、解答题：本大题共4个小题，每小题5分，共20分。‎ ‎16．计算 ‎ ‎17．先化简，再求值。其中，‎ ‎18．解不等式组 ‎19．在下面△ABC中，用尺规作出AB边上的高及∠B的平分线（不写作法，保留作图痕迹）‎ A B C 四、解答题：本大题3个小题，每小题6分，共18分。‎ ‎20．我市准备在相距2千米的A、B两工厂间修一条笔直的公路，但在B地北偏东60°方向、A地北偏西45°‎ 方向的C处，有一个半径为0.6千米的住宅小区（见下图），问修筑公路时，这个小区是否有居民需要搬迁？‎ ‎ （参考数据： ）‎ ‎21．从下面的6张牌中，任意抽取两张。求其点数和是奇数的概率。‎ ‎22如图，四边形ABCD是菱形，DE⊥AB交BA的延长线于E，DF⊥BC，交BC的延长线于F。‎ 请你猜想DE与DF的大小有什么关系？并证明你的猜想 五、解答题：本大题共2个小题，每小题7分，共14分。‎ ‎23．今年3月5日，花溪中学组织全体学生参加了“走出校门，服务社会”的活动。九年级一班高伟同学统计了该天本班学生打扫街道，去敬老院服务和到社区文艺演出的人数，并做了如下直方图和扇形统计图。请根据高伟同学所作的两个图形，解答：‎ ‎（1）九年级一班有多少名学生？‎ ‎（2）补全直方图的空缺部分。‎ ‎（3）若九年级有800名学生，估计该年级去敬老院的人数。‎ ‎24．如图，A、B为⊙O上的点，AC是弦，CD是⊙O的切线，C为切点，AD⊥CD于点D。若AC为∠BAD的平分线。‎ 求证：（1）AB为⊙O的直径 ‎（2）AC2＝AB·AD 六、解答题：本大题2个小题，每小题9分，共18分。‎ ‎25．抗震救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食，全部转移到具有较强抗震功能的A、B两仓库。已知甲库有粮食100吨，乙库有粮食80吨，而A库的容量为70吨，B库的容量为110吨。从甲、乙两库到A、B两库的路程和运费如下表（表中“元/吨·千米”表示每吨粮食运送1千米所需人民币）‎ ‎（1）若甲库运往A库粮食吨，请写出将粮食运往A、B两库的总运费（元）与（吨）的函数关系式 ‎（2）当甲、乙两库各运往A、B两库多少吨粮食时，总运费最省，最省的总运费是多少？‎ ‎26．抛物线的顶点为M，与轴的交点为A、B（点B在点A的右侧），△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b。若关于的一元二次方程有两个相等的实数根。‎ ‎（1）判断△ABM的形状，并说明理由。‎ ‎（2）当顶点M的坐标为（－2，－1）时，求抛物线的解析式，并画出该抛物线的大致图形。‎ ‎（3）若平行于轴的直线与抛物线交于C、D两点，以CD为直径的圆恰好与轴相切，求该圆的圆心坐标。‎ 参考答案 一、 选择题（每小题3分，共30分）‎ 一、 填空题（每小题4分，共20分）‎ ‎11．1.37×105 12．－2，－（答案不唯一） 13．10㎝2 14．10，20 15．3‎ 三、解答题（每小题5分，共20分）‎ ‎16．解：原式＝‎ ‎ ＝‎ ‎17．解：原式＝‎ ‎ ＝‎ ‎ 将，代入，则 原式＝‎ ‎18．解不等式（1），得 ‎ ‎ 解不等式（2），得 ‎ ‎ ‎∴原不等式无解 ‎19．略 四、解答题（每小题6分，共计18分）‎ ‎20．‎ 解：过点C作CD⊥AB于D ‎∴AD＝CD·cot45°＝CD BD＝CD·cot30°＝‎ ‎∵BD+AD＝AB＝2‎ ‎ 即+ CD＝2‎ ‎∴‎ 答：修的公路不会穿越小区，故该小区居民不需搬迁。‎ ‎21．解：可用列表法表示该事件所有和的可能情况 和 第一 第二 ‎4‎ ‎5‎ ‎6‎ ‎8‎ ‎9‎ ‎10‎ ‎4‎ ‎9‎ ‎10‎ ‎12‎ ‎13‎ ‎14‎ ‎5‎ ‎9‎ ‎11‎ ‎13‎ ‎14‎ ‎15‎ ‎6‎ ‎10‎ ‎11‎ ‎14‎ ‎15‎ ‎16‎ ‎8‎ ‎12‎ ‎13‎ ‎14‎ ‎17‎ ‎18‎ ‎9‎ ‎13‎ ‎14‎ ‎15‎ ‎17‎ ‎19‎ ‎10‎ ‎14‎ ‎15‎ ‎16‎ ‎18‎ ‎19‎ 从表中可看出，在这6张牌中任取两张牌，有30种可能结果，其中点数和为奇数的可能结果有16种，所以P(点数和为奇数)＝‎ ‎22． 解：DE＝DF ‎ 证明如下：‎ 连结BD ‎∵四边形ABCD是菱形 ‎∴∠CBD＝∠ABD(菱形的对角线平分一组对角)‎ ‎∵DF⊥BC，DE⊥AB ‎∴DF＝DE(角平分线上的点到角两边的距离相等)‎ 五、解答题：（每小题7分，共计14分）‎ ‎23．解（1）该班有50名学生 ‎ （2）去敬老院服务的学生有10人 图形如下 ‎（3）若全年级有800名学生，则估计去敬老院的人数为 ‎ 800×20％＝160（人）‎ ‎24．‎ 证明：（1）连结BC AC平分∠BAD ‎∴∠DAC＝∠CAB 又CD切⊙O于点C ‎∴∠ACD＝∠B(弦切角定理)‎ ‎∵AD⊥CD ‎ ∴∠ACD+∠DAC＝90°‎ ‎ 即∠B+∠CAB＝90°‎ ‎ ∴∠BCA＝90°‎ ‎∴AB是⊙O的直径（90°圆周角所对弦是直径）‎ ‎（2）∵∠ACD＝∠B ‎∠DAC＝∠CAB ‎ ∴△ACD∽△ABC ‎ ∴‎ ‎ ∴AC2＝AB·AD 六、解答题（每小题9分，共计18分）‎ ‎25．解（1）依题意有：‎ ‎ ‎ ‎ ＝‎ ‎ 其中 ‎ （2）上述一次函数中 ‎ ∴随的增大而减小 ‎ ∴当＝70吨时，总运费最省 ‎ 最省的总运费为：‎ 答：从甲库运往A库70吨粮食，往B库运送30吨粮食，从乙库运往B库80吨粮食时，总运费最省为37100元。‎ ‎25．解：（1）令 ‎ 得 ‎ 由勾股定理的逆定理和抛物线的对称性知 ‎△ABM是一个以、为直角边的等腰直角三角形 ‎ （2）设 ‎∵△ABM是等腰直角三角形 ‎∴斜边上的中线等于斜边的一半 又顶点M(－2，－1)‎ ‎∴，即AB＝2‎ ‎∴A(－3，0)，B(－1，0)‎ 将B(－1，0) 代入中得 ‎∴抛物线的解析式为，即 图略 ‎（3）设平行于轴的直线为 解方程组 得， （‎ ‎∴线段CD的长为 ‎∵以CD为直径的圆与轴相切 据题意得 ‎∴‎ 解得 ‎ ‎∴圆心坐标为和