2009年浙江省丽水市数学试题卷及答案 10页

浙江省2009年初中毕业生学业考试（丽水市卷）‎ 数学试题卷 考生须知：‎ ‎1、全卷满分为120分，考试时间为120分钟．‎ ‎2、答题前，请在答题卡上先填写姓名和准考证号，再用铅笔将准考证号和科目对应的括号或方 框涂黑．‎ ‎3、请在“答题卷Ⅱ”上填写座位号并在密封线内填写县（市、区）学校、姓名和准考证号．‎ ‎4、本卷答案必须做在答题卷Ⅰ、Ⅱ的相应位置上，做在试卷上无效．答题时，不允许使用计算 器.‎ 温馨提示：带着愉悦的心情，载着自信与细心，凭着沉着与冷静，迈向理想的彼岸！ ‎ 试 卷 Ⅰ 一、选择题（本题有10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）‎ ‎1．在下列四个数中，比0小的数是 A. 0.5‎ B. ‎-2 C. 1 D. 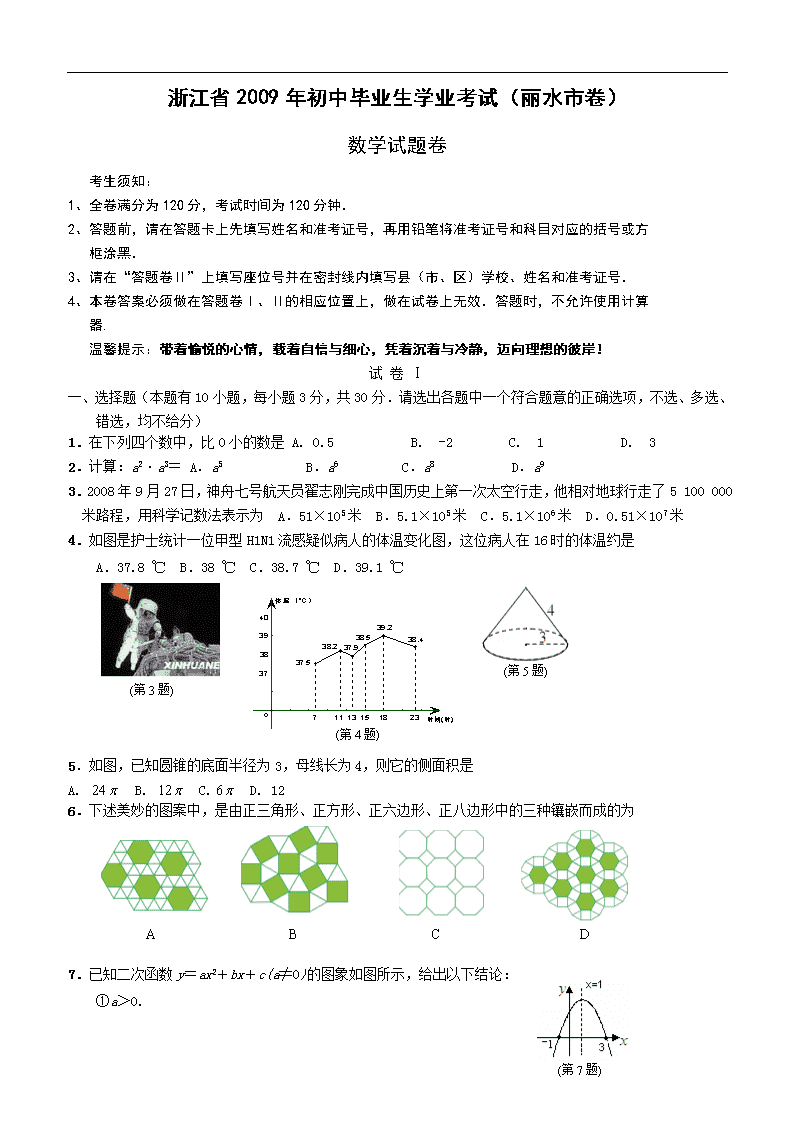3‎ ‎2．计算：a2·a3＝ A．a5 B．a‎6 C．a8 D．a9‎ ‎3．‎2008年9月27日，神舟七号航天员翟志刚完成中国历史上第一次太空行走，他相对地球行走了5 100 000‎ ‎ 米路程，用科学记数法表示为 A．51×‎105米 B．5.1×‎105米 C．5.1×‎106米 D．0.51×‎‎107米 ‎4．如图是护士统计一位甲型H1N1流感疑似病人的体温变化图，这位病人在16时的体温约是 ‎(第5题)‎ ‎·‎ A．‎37.8 ℃‎ B．‎38 ℃‎ ‎(第3题)‎ C．‎38.7 ℃‎ D．‎‎39.1 ℃‎ ‎(第4题)‎ ‎5．如图，已知圆锥的底面半径为3，母线长为4，则它的侧面积是 ‎ A. B. C. D. 12‎ A B C D ‎6．下述美妙的图案中，是由正三角形、正方形、正六边形、正八边形中的三种镶嵌而成的为 ‎(第7题)‎ ‎7．已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，给出以下结论：‎ ‎①a＞0.‎ O ‎②该函数的图象关于直线对称.‎ ‎③当时，函数y的值都等于0.‎ 其中正确结论的个数是 A．3 B．2 C．1 D．0‎ P ‎(第8题)‎ ‎8．如图，点在反比例函数(x > 0)的图象上，且横坐标为2. 若将点先向右平移两个单位，再向上平移一个单位后所得的像为点.则在第一象限内，经过点的反比例函数图象的解析式是 A． B. C. D. ‎ ‎(第9题)‎ 主视图 俯视图 ‎9．如图，是由一些大小相同的小正方体组成的几何体的主视图和俯视图， ‎ 则组成这个几何体的小正方体最多块数是‎ A. 9 B. 10 ‎ C. 11 D. 12　 ‎ ‎(第10题)‎ l1‎ l2‎ l3‎ A C B ‎10．如图，已知△ABC中，∠ABC=90°,AB=BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为2 , l2，l3之间的距离为3 ,则AC的长是 A． B． C． D．7‎ 试卷Ⅱ 说明：本卷有二大题，14小题，共90分，请将本卷的答案或解答过程用钢笔或圆珠笔写在答题卷Ⅱ上．‎ ‎(第12题)‎ 二、填空题（本题有6小题，每小题4分，共24分）‎ ‎11．当x ▲ 时，分式没有意义．‎ ‎12．如图，在⊙O中，∠ABC=40°，则∠AOC＝ ▲ 度． ‎ ‎13．用配方法解方程时，方程的两边同加上 ▲ ，使得方程左边配成一个完全平方式．‎ ‎(第14题)‎ ‎14.如图所示是两个各自分割均匀的转盘，同时转动两个转盘，转盘停止 ‎ 时（若指针恰好停在分割线上，那么重转一次，直到指针指向某一区域 ‎ 为止），两个指针所指区域的数字和为偶数的概率是 ▲ . 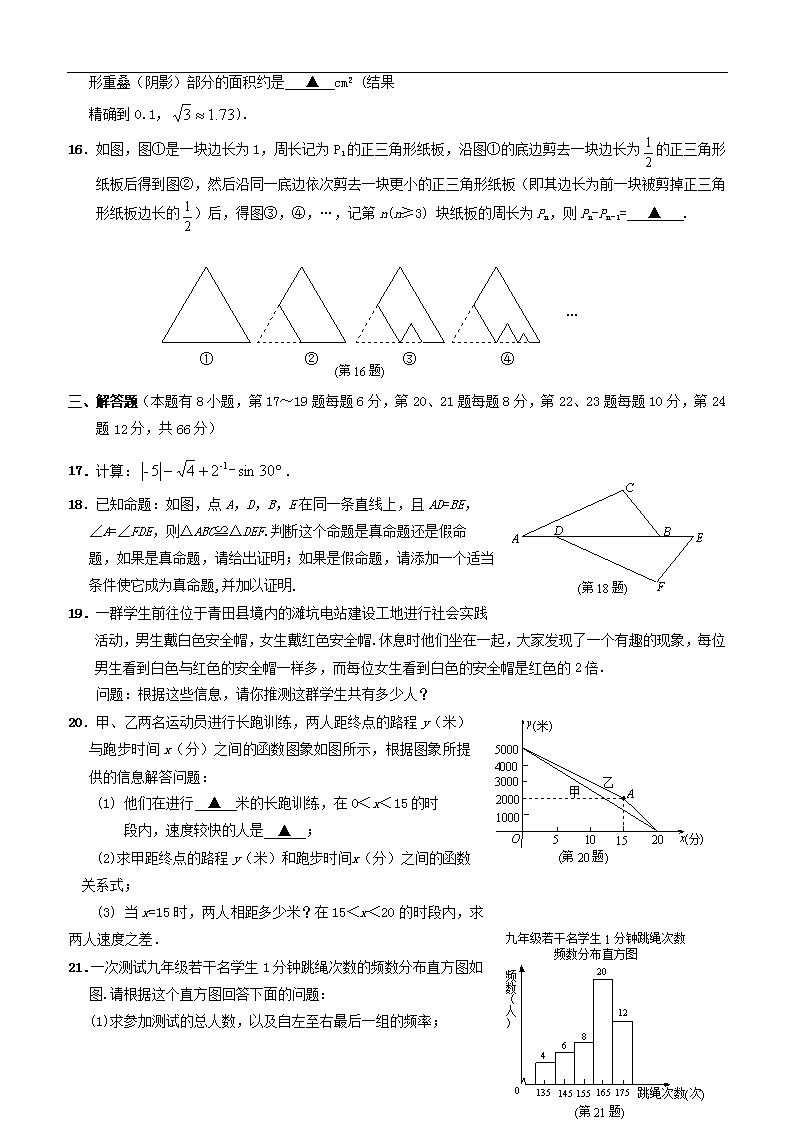‎ ‎(第15题)‎ ‎15．将一副三角板按如图1位置摆放,使得两块三角板 的直角边AC和MD重合.已知AB=AC=‎8 cm,将 ‎△MED绕点A(M)逆时针旋转60°后(图2),两个三角 形重叠（阴影）部分的面积约是 ▲ cm2 (结果 ‎ 精确到0.1，).‎ ‎(第16题)‎ ‎…‎ ‎① ② ③ ④ ‎ ‎16．如图，图①是一块边长为1，周长记为P1的正三角形纸板，沿图①的底边剪去一块边长为的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪掉正三角形纸板边长的）后，得图③，④，…，记第n(n≥3) 块纸板的周长为Pn，则Pn-Pn-1= ▲ .‎ ‎ ‎ 三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）‎ ‎(第18题)‎ ‎17．计算：-．‎ ‎18．已知命题：如图，点A，D，B，E在同一条直线上，且AD=BE，‎ ‎ ∠A=∠FDE，则△ABC≌△DEF.判断这个命题是真命题还是假命 ‎ 题，如果是真命题，请给出证明；如果是假命题，请添加一个适当 ‎ 条件使它成为真命题,并加以证明.‎ ‎19．一群学生前往位于青田县境内的滩坑电站建设工地进行社会实践活动，男生戴白色安全帽，女生戴红色安全帽.休息时他们坐在一起，大家发现了一个有趣的现象，每位男生看到白色与红色的安全帽一样多，而每位女生看到白色的安全帽是红色的2倍.‎ ‎(第20题)‎ 问题：根据这些信息，请你推测这群学生共有多少人？‎ ‎20．甲、乙两名运动员进行长跑训练，两人距终点的路程y（米）与跑步时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答问题：‎ ‎(1) 他们在进行 ▲ 米的长跑训练，在0＜x＜15的时 ‎ 段内，速度较快的人是 ▲ ；‎ ‎(2) 求甲距终点的路程y（米）和跑步时间 x（分）之间的函数关系式；‎ ‎(3) 当x=15时，两人相距多少米？在15＜x＜20的时段内，求两人速度之差．‎ ‎(第21题)‎ 跳绳次数(次)‎ 九年级若干名学生1分钟跳绳次数 频数分布直方图 频数（人）‎ ‎21．一次测试九年级若干名学生1分钟跳绳次数的频数分布直方图如图.请根据这个直方图回答下面的问题：‎ ‎(1)求参加测试的总人数，以及自左至右最后一组的频率；‎ ‎(2)若图中自左至右各组的跳绳平均次数分别为137次,‎ ‎146次,156次,164次,177次.小丽按以下方法计算参 加测试学生跳绳次数的平均数是：‎ ‎(137+146＋156＋164＋177)÷5＝156．‎ 请你判断小丽的算式是否正确，若不正确，写 ‎ 出正确的算式（只列式不计算）；‎ ‎(3)如果测试所得数据的中位数是160次，那么测试次数为160次的学生至少有多少人？‎ ‎22．绿谷商场“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示：‎ 类别 冰箱 彩电 进价（元/台）‎ ‎2 320‎ ‎1 900‎ 售价（元/台）‎ ‎2 420‎ ‎1 980‎ ‎(1) 按国家政策，农民购买“家电下乡”产品可享受售价13%的政府补贴.农民田大伯到该商场购买 了冰箱、彩电各一台，可以享受多少元的政府补贴？‎ ‎(2)为满足农民需求,商场决定用不超过85 000元采购冰箱、彩电共40台, 且冰箱的数量不少于彩电数量的. ‎ ‎①请你帮助该商场设计相应的进货方案；‎ ‎②哪种进货方案商场获得利润最大（利润=售价进价），最大利润是多少？‎ ‎(第23题)‎ ‎23．如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥ ‎ ‎ AC交AB于点D.‎ ‎(1)尺规作图：过A，D，C三点作⊙O（只要求作出图形，‎ ‎ 保留痕迹，不要求写作法）；‎ ‎(2)求证：BC是过A，D，C三点的圆的切线；‎ ‎(3)若过A，D，C三点的圆的半径为,则线段BC上是否存在一点P，使得以P，D，B为顶点的三角 形与△BCO相似.若存在，求出DP的长；若不存在，请说明理由.‎ ‎24. 已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为(4,0)，(0,3).现有两动点P,Q分别从A,C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒.‎ ‎(第24题)‎ ‎(1)填空：菱形ABCD的边长是 ▲ 、面积是 ▲ 、 ‎ 高BE的长是 ▲ ；‎ ‎(2)探究下列问题：‎ ‎①若点P的速度为每秒1个单位，点Q的速度为每秒2个单位.当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式，以及S的最大值； ‎ ‎②若点P的速度为每秒1个单位，点Q的速度变为每秒k 个单位，在运动过程中,任何时刻都有相应的k值，使得 ‎△APQ沿它的一边翻折，翻折前后两个三角形组成的四边 形为菱形.请探究当t=4秒时的情形，并求出k的值.‎ 浙江省2009年初中毕业生学业考试（丽水市卷）‎ 数学试卷参考答案和评分标准细则 一. 选择题（本题共10小题，每小题3分，共30分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B A C C B D B ‎ D C A 评分标准 选对一题给3分，不选，多选，错选均不给分 二、填空题（本题有6小题，每小题4分，共24分）‎ ‎11．x＝0； 12．80； 13．4 ； 14．； 15．20.3 16．‎ 三、解答题 （本题有8题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）‎ ‎17．（本题6分）‎ 解：原式=5-2+- ………………………………4分 ‎ =3. ………………………………2分 ‎18．（本题6分）‎ ‎(第18题)‎ ‎ 解：是假命题.………………………………1分 以下任一方法均可：‎ ‎ ①添加条件：AC=DF. ………………1分 证明：∵AD=BE,‎ ‎∴AD+BD=BE+BD，即AB=DE. …1分 在△ABC和△DEF中,‎ AB=DE，‎ ‎∠A=∠FDE，‎ AC=DF， ………………………………………………………2分 ‎∴△ABC≌△DEF(SAS). ………………………………………………………1分 ‎②添加条件：∠CBA=∠E. ……………………………………1分 证明：∵AD=BE, ‎ ‎∴AD+BD=BE+BD,即AB=DE. ………………………………………………1分 在△ABC和△DEF中，‎ ‎∠A=∠FDE，‎ AB=DE，‎ ‎∠CBA=∠E ， ……………………………………………………………2分 ‎∴△ABC≌△DEF(ASA). ………………………………………………………1分 ‎③添加条件：∠C=∠F. ………………………………………………………………1分 证明：∵AD=BE,‎ ‎∴AD+BD=BE+BD,即AB=DE. ………………………………………………1分 在△ABC和△DEF中，‎ ‎∠A=∠FDE，‎ ‎∠C=∠F ，‎ AB=DE， ………………………………………………………………2分 ‎∴△ABC≌△DEF(AAS) ………………………………………………………1分 ‎19．（本题6分）‎ 解法一：设男生有x人，则女生有（x-1）人. …………………………………………1分 根据题意，得x=2(x-1-1) ……………………………………………………2分 解得x=4， ………………………………………………………………………1分 x-1=3. ………………………………………………………………………1分 答：这群学生共有7人. ………………………………………………………1分 解法二：设男生有x人，女生有y人. ………………………………………………1分 根据题意，得……………………………………………………2分 ‎ 解得 …………………………………………………………………2分 ‎ 答：这群学生共有7人. ………………………………………………………1分 ‎(第20题)‎ ‎20．（本题8分）‎ 解：（1）5000…………………………………1分 甲 ………………………………1分 ‎（2）设所求直线的解析式为：‎ y =kx+b(0≤x≤20)， ………1分 由图象可知：b=5000，当x=20时，y=0，‎ ‎∴0=20k+5000，解得k= -250. …1分 即y = -250x+5000 (0≤x≤20) ……………1分 ‎（3）当x=15时，y = -250x+5000= -250×15+5000=5000-3750=1250. …………1分 两人相距：(5000 -1250)-(5000-2000)=750（米）. …………………1分 两人速度之差:750÷(20-15)=150（米/分） ………………1分 ‎21.（本题8分）‎ 解：（1）50 ………………………………………………………………………………1分 ‎ ‎12÷50＝0.24 ……………………………………………………………………1分 ‎ ‎（2）不正确.…………………………………………………………………………1分 正确的算法：(137×4+146×6＋156×8＋164×20＋177×12)÷50． ……………2分 ‎（3）∵组距为10,‎ ‎∴第四组前一个边界值为160, ………………………………………………1分 又∵第一、二、三组的频数和为18,‎ ‎∴50÷2-18+1＝8 ，即次数为160次的学生至少有8人. ……………………2分 ‎22．（本题10分）‎ 解：(1) (2 420+1 980)×13%=572 …………(3分)‎ 答: 可以享受政府572元的补贴. ‎ ‎ (2) ①设冰箱采购x台，则彩电采购（40-x）台，根据题意，得 ………(1分)‎ ‎2 320x+1 900(40-x)≤85 000，‎ x≥(40-x). ‎ 解不等式组，得≤x≤ ……………(3分)‎ ‎ ∵x为正整数． ‎ ‎ ∴x= 19,20，21．‎ ‎ ∴该商场共有3种进货方案：‎ 方案一：冰箱购买19台，彩电购买21台 方案二：冰箱购买20台，彩电购买20台；‎ 方案三：冰箱购买21台，彩电购买19台. ………(1分)‎ ‎②设商场获得总利润y元，根据题意，得 ‎ y=(2 420 - 2 320)x+(1 980 -1 900)(40-x)=20x+3 200‎ ‎∵20>0, ∴y随x的增大而增大 ‎∴当x=21时，y最大=20×21+3 200=3 620‎ 答：方案三商场获得利润最大，最大利润是3 620元 ………(2分)‎ ‎23．（本题10分）‎ 解：（1）作出圆心O， ………………………………………………………………1分 以点O为圆心，OA长为半径作圆.…………………………………………1分 ‎（2）证明：∵CD⊥AC,∴∠ACD=90°. ‎ ‎∴AD是⊙O的直径……………1分 连结OC，∵∠A=∠B=30°,‎ ‎∴∠ACB=120°,又∵OA=OC, ‎ ‎∴∠ACO=∠A =30°,…………1分 ‎∴∠BCO=∠ACB-∠ACO =120°-30°=90°. ………………1分 ‎∴BC⊥OC,‎ ‎∴BC是⊙O的切线. ……………………………………………1分 ‎（3）存在. ……………………………………………………………………………1分 ‎∵∠BCD=∠ACB-∠ACD=120°-90°=30°,‎ ‎∴∠BCD=∠B, 即DB=DC.‎ 又∵在Rt△ACD中，DC=AD, ∴BD= . ……………1分 解法一：①过点D作DP1// OC，则△P1D B∽△COB, ，‎ ‎ ∵BO=BD+OD=,‎ ‎∴P1D=×OC=× =. ……………………………1分 ‎ ②过点D作DP2⊥AB,则△BDP2∽△BCO, ∴，‎ ‎ ∵BC＝‎ ‎∴.………………………………………1分 解法二：①当△B P1D∽△BCO时，∠DP1B=∠OCB=90°.‎ 在Rt△B P1D中，‎ DP1=. ………………1分 ‎②当△B D P2∽△BCO时，∠P2DB=∠OCB=90°.‎ 在Rt△B P2D中，‎ DP2=. ……………1分 ‎24．（本题12分）‎ 解：（1）5 , 24, …………………………………3分 ‎（2）①由题意，得AP=t，AQ=10-2t. …………………………………………1分 如图1,过点Q作QG⊥AD，垂足为G，由QG∥BE得 ‎ ‎△AQG∽△ABE,∴,‎ ‎∴QG=, …………………………1分 ‎∴(≤t≤5). ‎ ‎……1分 ‎∵(≤t≤5).‎ ‎∴当t=时，S最大值为6.…………………1分 ‎② 要使△APQ沿它的一边翻折，翻折前后的两个三角形组 成的四边形为菱形，根据轴对称的性质，只需△APQ为等腰三角形即可.‎ 当t=4秒时，∵点P的速度为每秒1个单位，∴AP=.………………1分 以下分两种情况讨论:‎ 第一种情况：当点Q在CB上时, ∵PQ≥BE>PA，∴只存在点Q1,使Q‎1A=Q1P.‎ 如图2,过点Q1作Q1M⊥AP，垂足为点M，Q1M交AC于点 F,则AM=.由△AMF∽△AOD∽△CQ1F,得 ‎, ∴,‎ ‎∴. ………………1分 ‎∴CQ1==.则, ∴ .……………………………1分 第二种情况：当点Q在BA上时,存在两点Q2,Q3,‎ 分别使A P= A Q2,PA=PQ3.‎ ‎①若AP=AQ2，如图3,CB+BQ2=10-4=6.‎ 则,∴.……1分 ‎ ‎②若PA=PQ3，如图4,过点P作PN⊥AB，垂足为N，‎ 由△ANP∽△AEB,得. ‎ ‎∵AE= , ∴AN＝.‎ ‎∴AQ3=2AN=, ∴BC+BQ3=10-‎ 则.∴. ‎ ‎………………………1分 综上所述，当t= 4秒，以所得的等腰三角形APQ 沿底边翻折，翻折后得到菱形的k值为或或.‎