2009年山东省威海市初中升学考试数学试卷及参考答案 11页

试卷类型：A 威海市二○○九年初中升学考试 数 学 亲爱的同学： 你好！答题前，请仔细阅读以下说明： 1. 本试卷共 12 页，分第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷（1-4 页）为选择题，第Ⅱ卷（5-12 页）为非选择题．试卷满分 120 分．考试时间 120 分钟． 2. 请清点试卷，然后将考生信息填涂在答题卡上，并将第Ⅱ卷密封线内的项目填写清楚． 3. 将选择题答案用 2B 铅笔涂在答题卡对应题目的标号上，将非选择题答案用蓝色或黑色 钢笔、圆珠笔填写在试卷上．不要求保留精确度的题目，计算结果保留准确值． 希望你能愉快地度过这 120 分钟，祝你成功！ 第Ⅰ卷（选择题，共 36 分） 一、选择题（本大题共 12 小题，每小题 3 分，共 36 分，在每小题给出的四个选项中，只 有一个是正确的．每小题选对得 3 分，选错、不选或多选，均不得分） 1． 3 27 的绝对值是（ ） A．3 B． 3 C． 1 3 D． 1 3  2．如图，AB AC BD BC ， ，若 40A   ，则 ABD 的度数是（ ） A． 20 B．30 C．35 D． 40 3．实数 a b， 在数轴上的位置如图所示，则下列结论正确的是（ ） A. 0a b  B. 0a b  C. 0a b  D． 0a b  4．形状相同、大小相等的两个小木块放置于桌面，其俯视图如下图所示，则其主视图是 （ ） 5．化简 1 1y xx y           的结果是（ ） A. y x  B． x y  C． x y D． y x 6．某公司员工的月工资如下表： 1 a 0 1 b B A D C （俯视图） A． B． C． D． 员工 经理 副经理 职员 A 职员 B 职员 C 职员 D 职员 E 职员 F 职员G 月工资/元 4800 3500 2000 1900 1800 1600 1600 1600 1000 则这组数据的平均数、众数、中位数分别为（ ） A．2200 元 1800 元 1600 元 B．2000 元 1600 元 1800 元 C．2200 元 1600 元 1800 元 D．1600 元 1800 元 1900 元 7．二次函数 23 6 5y x x    的图象的顶点坐标是（ ） A． ( 18) ， B． (18)， C． ( 1 2) ， D． (1 4)， 8．在梯形 ABCD 中， // 60 30 6AB CD A B AD CD      ， ， ， ，则 AB 的长度为 （ ） A．9 B．12 C．18 D．6 3 3 9．如图，A，B 的坐标为（2，0），（0，1）若将线段 AB 平 移至 1 1A B ，则 a b 的值为（ ） A．2 B．3 C．4 D．5 10．如图，在四边形 ABCD 中，E 是 BC 边的中点，连结 DE 并延长，交 AB 的延长线于 F 点， AB BF ．添 加一个条件，使四边形 ABCD 是平行四边形．你认为 下面四个条件中可选择的是（ ） A． AD BC B．CD BF C． A C   D． F CDE   11．已知 O 是 ABC△ 的外接圆，若 AB=AC=5，BC=6，则 O 的半径为（ ） A．4 B．3.25 C．3.125 D．2.25 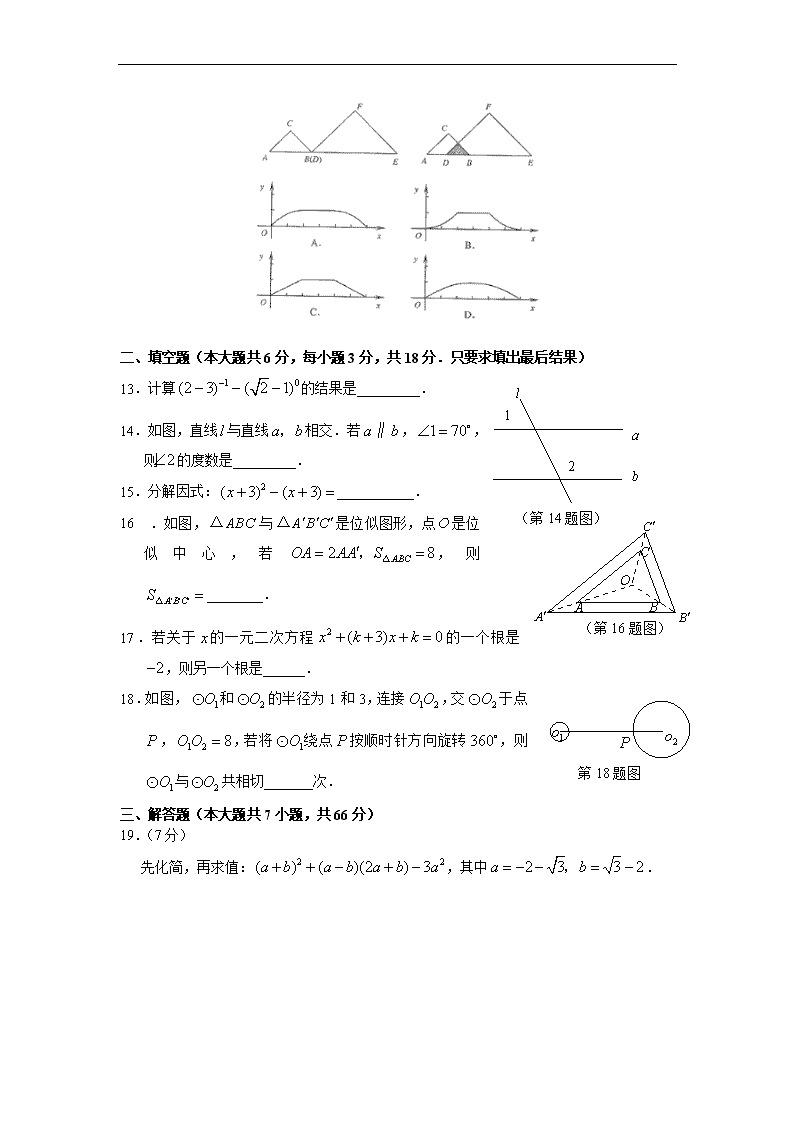12 ． 如 图 ， ABC△ 和 的 DEF△ 是 等 腰 直 角 三 角 形 ， 90C F     ， 2 4AB DE ， ．点 B 与点 D 重合，点 A B D E，（ ）， 在同一条直线 上，将 ABC△ 沿 D E 方向平移，至点 A 与点 E 重合时停止．设点 B D， 之间的距离为 x， ABC△ 与 DEF△ 重叠部分的面积为 y ，则准确反映 y 与 x 之间对应关系的图象是（ ） y O (01)B ， (2 0)A ， 1(3 )A b， 1( 2)B a， x E BA F CD 二、填空题（本大题共 6 分，每小题 3 分，共 18 分．只要求填出最后结果） 13．计算 1 0(2 3) ( 2 1)   的结果是_________． 14．如图，直线 l 与直线 a b， 相交．若 a b∥ ， 1 70   ， 则 2 的度数是_________． 15．分解因式： 2( 3) ( 3)x x    ___________． 16．如图， ABC△ 与 A B C  △ 是位似图形，点 O 是位似 中 心 ， 若 2 8ABCOA AA S △， ， 则 A B CS    △ ________． 17．若关于 x 的一元二次方程 2 ( 3) 0x k x k    的一个根是 2 ，则另一个根是______． 18．如图， 1O 和 2O 的半径为 1 和 3，连接 1 2O O ，交 2O 于点 P ， 1 2 8O O  ，若将 1O 绕点 P 按顺时针方向旋转 360 ，则 1O 与 2O 共相切_______次． 三、解答题（本大题共 7 小题，共 66 分） 19．（7 分） 先化简，再求值： 2 2( ) ( )(2 ) 3a b a b a b a     ，其中 2 3 3 2a b    ， ． 1o 2oP 第 18 题图 C O A B B C A （第 16 题图） b a l 2 1 （第 14 题图） 20．（7 分） 除颜色外完全相同的六个小球分别放到两个袋子中，一个袋子中放两个红球和一个白 球，另一个袋子中放一个红球和两个白球．随机从两个袋子中分别摸出一个小球，试判断摸 出两个异色小球的概率与摸出两个同色小球的概率是否相等，并说明理由． 21.（9 分） 如图，一巡逻艇航行至海面 B 处时，得知其正北方向上 C 处一渔船发生故障．已知港 口 A 处在 B 处的北偏西37 方向上，距 B 处 20 海里；C 处在 A 处的北偏东 65 方向上． 求 ,B C 之间的距离（结果精确到 0.1 海里）． 参考数据：sin37 0.60 cos37 0.80 tan37 0.75    ， ， ， sin 65 0.91 cos65 0.42 tan 65 2.14.    ， ， 22.（10 分） 响应“家电下乡”的惠农政策，某商场决定从厂家购进甲、乙、丙三种不同型号的电冰 箱 80 台，其中甲种电冰箱的台数是乙种电冰箱台数的 2 倍，购买三种电冰箱的总金额不超．． 过．132 000 元．已知甲、乙、丙三种电冰箱的出厂价格分别为：1 200 元/台、1 600 元/台、2 000 元/台． (1)至少购进乙种电冰箱多少台？ (2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数，则有哪些购买方案？ 65° 37° 北 北 A C B 23.（10 分） 如图 1，在正方形 ABCD 中， E F G H， ， ， 分别为边 AB BC CD DA， ， ， 上的点， HA EB FC GD   ，连接 EG FH， ，交点为O ． （1）如图 2，连接 EF FG GH HE， ， ， ，试判断四边形 EFGH 的形状，并证明你的 结论； （2）将正方形 ABCD 沿线段 ,EG HF 剪开，再把得到的四个四边形按图 3 的方式拼接 成一个四边形．若正方形 ABCD 的边长为 3cm， 1cmHA EB FC GD    ，则图 3 中 阴影部分的面积为_________ 2cm ． 24．（11 分） 如图，在直角坐标系中，点 A B C， ， 的坐标分别为 ( 1 0) (3 0) (0 3) ，，，，， ，过 A B C， ， 三 （第 23 题图 1） D C BA OH G F E E BA D CG F H （第 23 题图 2） （第 23 题图 3） OA B C ly x 点的抛物线的对称轴为直线l D， 为对称轴l 上一动点． (1)求抛物线的解析式； (2)求当 AD CD 最小时点 D 的坐标； (3)以点 A 为圆心，以 AD 为半径作 A ． ①证明：当 AD CD 最小时，直线 BD 与 A 相切． ②写出直线 BD 与 A 相切时， D 点的另一个坐标：___________． 25．（12 分） 一次函数 y ax b  的图象分别与 x 轴、 y 轴交于点 ,M N ，与反比例函数 ky x  的图 象相交于点 ,A B ．过点 A 分别作 AC x 轴， AE y 轴，垂足分别为 ,C E ；过点 B 分别 作 BF x 轴， BD y 轴，垂足分别为 F D， ，AC 与 BD 交于点 K ，连接CD ． （1）若点 A B， 在反比例函数 ky x  的图象的同一分支上，如图 1，试证明： ① AEDK CFBKS S四边形 四边形 ； ② AN BM ． （2）若点 A B， 分别在反比例函数 ky x  的图象的不同分支上，如图 2，则 AN 与 BM 还 相等吗？试证明你的结论． O C F M D E N K y x 1 1( )A x y， 2 2( )B x y， （第 25 题图 1） O C D K F E N y x 1 1( )A x y， 3 3( )B x y， M （第 25 题图 2） 威海市 2009 年初中升学考试 数学试题参考解答及评分意见 评卷说明： 1． 第一大题（选择题）和第二大题（填空题）的每小题，只有满分和零分两个评分档，不 给中间分． 2． 第三大题（解答题）每小题的解答中所对应的分数，是指考生正确解答到该步骤所应得 的累计分数．部分试题有多种解法，对考生的其他解法，请参考评分意见进行评分． 3． 如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部 分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分就 不再给分． 一、选择题（本大题共 12 小题，每小题 3 分，共 36 分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B A D D C A C A D C B 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分） 13． 2 ； 14．110°； 15． ( 2)( 3)x x  16．18； 17．1； 18．3． 三、解答题（本大题共 7 小题，共 66 分） 19．（本小题满分 7 分） 解： 2 2 2 2 2 2 2( ) ( )(2 ) 3 2 2 3a b a b a b a a ab b a ab b a            ················· 3 分 ab ．··········································································································5 分 当 2 3a    ， 3 2b   时， 原式 2 2( 2 3)( 3 2) ( 2) ( 3) 1        ·······················································7 分 20．（本小题满分 7 分） 解：摸出两个异色小球的概率与摸出两个同色小球的概率不相等．····························1 分 画树状图如下（画出一种情况即可）： ··································4 分 ∴摸出两个异色小球的概率为 5 9 ，······································································ 5 分 摸出两个同色小球的概率 4 9 ．············································································6 分 即摸出两个异色小球的概率与摸出两个同色小球的概率不相等．·······························7 分 21．（本小题满分 9 分） 解：过点 A 作 AD BC ，垂足为 D．·····················1 分 在 Rt ABD△ 中， 20AB  ， 37B  °， ∴ sin37 20sin37 12AD AB · ° °≈ ．················· 3 分 cos37 20cos37 16BD AB · ° °≈ ．··················· 5 分 在 Rt ADC△ 中， 65ACD  °， ∴ 12 5.61tan 65 2.14 ADCD  ≈ ≈° ···························· 8 分 5.61 16 21.61 21.6BC BD CD    ≈ ≈ （海里） 答： B C， 之间的距离约为 21.6 海里．································································9 分 22．（本小题满分 10 分） 解：（1）设购买乙种电冰箱 x 台，则购买甲种电冰箱 2x 台， 丙种电冰箱 (80 3 )x 台，根据题意，列不等式：···················································1 分 1200 2 1600 (80 3 ) 2000 132000x x x     ≤ ．················································3 分 解这个不等式，得 14x≥ ．·············································································· 4 分 至少购进乙种电冰箱 14 台．···········································································5 分 （2）根据题意，得 2 80 3x x≤ ．···································································· 6 分 解这个不等式，得 16x ≤ ．·············································································· 7 分 由（1）知 14x≥ ． 14 16x ≤ ≤ ． 又 x 为正整数， 141516x  ，， ．·····························································································8 分 所以，有三种购买方案： 方案一：甲种电冰箱为 28 台，乙种电冰箱为 14 台，丙种电冰箱为 38 台； 方案二：甲种电冰箱为 30 台，乙种电冰箱为 15 台，丙种电冰箱为 35 台； 方案三：甲种电冰箱为 32 台，乙种电冰箱为 16 台，丙种电冰箱为 32 台．··············· 10 分 23．（本小题满分 10 分） 红 白 白 红 红 白 白 红 红 白 白 白 开始 或 红 红 白 白 红 红 白 白 红 红 白 红 开始 65° 37° 北 北 A C B D 解：（1）四边形 EFGH 是正方形．·····················1 分 证明：四边形 ABCD 是正方形，  90A B C D AB BC CD DA          °， . HA EB FC GD   ， AE BF CG DH    ．·······························2 分 AEH BFE CGF DHG△ ≌△ ≌△ ≌△ ．······· 3 分 EF FG GH HE    ．·······························4 分 四边形 EFGH 是菱形．·································5 分 由 DHG AEH△ ≌△ 知 DHG AEH   ． 90AEH AHE    °， 90DHG AHE    °． 90GHE  °．···························································································6 分 四边形 EFGH 是正方形．············································································· 7 分 （2）1．······································································································ 10 分 24．（本小题满分 11 分） 解：（1）设抛物线的解析式为 ( 1)( 3)y a x x   ．················································1 分 将 (0 3)， 代入上式，得 3 (0 1)(0 3)a   ． 解，得 1a   ．······························································································2 分 抛物线的解析式为 ( 1)( 3)y x x    ． 即 2 2 3y x x    ．·······················································································3 分 （2）连接 BC ，交直线l 于点 D ． 点 B 与点 A 关于直线 l 对称， AD BD  ．······················································ 4 分 AD CD BD CD BC     ． 由“两点之间，线段最短”的原理可知： 此时 AD CD 最小，点 D 的位置即为所求．·············· 5 分 设直线 BC 的解析式为 y kx b  ， 由直线 BC 过点 (3 0)， ， (0 3)， ，得 0 3 3 . k b b     ， 解这个方程组，得 1 3. k b     ， 直线 BC 的解析式为 3y x   ．····································································6 分 由（1）知：对称轴l 为 2 12 ( 1)x     ，即 1x  ． 将 1x  代入 3y x   ，得 1 3 2y     ． E BA D CG F H 图 2 O OA B C ly x D E 点 D 的坐标为（1，2）．················································································ 7 分 说明：用相似三角形或三角函数求点 D 的坐标也可，答案正确给 2 分． （3）①连接 AD ．设直线l 与 x 轴的交点记为点 E ． 由（1）知：当 AD CD 最小时，点 D 的坐标为（1，2）． 2DE AE BE    ． 45DAB DBA    °．·············································································· 8 分 90ADB  °． AD BD ⊥ ． BD 与 A⊙ 相切．·························································································9 分 ② (1 2)， ．·································································································· 11 分 25．（本小题满分 12 分） 解：（1）① AC x ⊥ 轴， AE y⊥ 轴， 四边形 AEOC 为矩形．  BF x⊥ 轴， BD y⊥ 轴， 四边形 BDOF 为矩形． AC x ⊥ 轴， BD y⊥ 轴， 四边形 AEDK DOCK CFBK， ， 均为矩形．···········1 分  1 1 1 1OC x AC y x y k  ， ， ，  1 1AEOCS OC AC x y k   矩形  2 2 2 2OF x FB y x y k  ， ， ，  2 2BDOFS OF FB x y k   矩形 ．  AEOC BDOFS S矩形 矩形 ．  AEDK AEOC DOCKS S S 矩形 矩形 矩形 ， CFBK BDOF DOCKS S S 矩形 矩形 矩形 ，  AEDK CFBKS S矩形 矩形 ．·················································································· 2 分 ②由（1）知 AEDK CFBKS S矩形 矩形 ．  AK DK BK CK  ．  AK BK CK DK  ．······························································································4 分  90AKB CKD    °，  AKB CKD△ ∽△ ．····················································································5 分 O C F M D E N K y x A B 图 1  CDK ABK   ．  AB CD∥ ．······························································································· 6 分  AC y∥ 轴， 四边形 ACDN 是平行四边形．  AN CD ．······························································································· 7 分 同理 BM CD ． AN BM  ．·······························································································8 分 （2） AN 与 BM 仍然相等．············································································· 9 分  AEDK AEOC ODKCS S S 矩形 矩形 矩形 ， BKCF BDOF ODKCS S S 矩形 矩形 矩形 ， 又 AEOC BDOFS S k 矩形 矩形 ，  AEDK BKCFS S矩形 矩形 ．·····························10 分  AK DK BK CK  ．  CK DK AK BK  ．  K K   ，  CDK ABK△ ∽△ ．  CDK ABK   ．  AB CD∥ ．······························································································11 分  AC y∥ 轴， 四边形 ANDC 是平行四边形．  AN CD ． 同理 BM CD ．  AN BM ．·····························································································12 分 O C D K F E N y x A B M 图 2