中考数学复习专题四边形的性质和判定无答案 5页

四边形性质探索 第一部分 知识梳理 ‎ 1.平行四边形 ‎ ①定义：两组对边分别平行的四边形是平行四边形．‎ ‎ ②性质：平行四边形的对边平行且相等；平行四边形的邻角互补，对角相等；平行四边形的对角线互相平分；平行四边形是中心对称图形，对角线的交点为对称中心；‎ ‎ ③判定方法 ‎ 定义：两组对边分别平行的四边形是平行四边形；‎ ‎ 判定方法1：两组对边分别相等的四边形是平行四边形；‎ ‎ 判定方法2：两组对角分别相等的四边形是平行四边形；‎ 判定方法3：对角线互相平分的四边形是平行四边形；‎ 判定方法4：一组对边平行且相等的四边形是平行四边形．‎ ‎ 2.菱形 ‎ ①定义：有一组邻边相等的平行四边形叫做菱形．‎ ‎ ②性质：具有平行四边形的一切特征；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形的面积等于对角线乘积的一半；菱形是轴对称图形．‎ ‎ ③判定方法 定义：有一组邻边相等的平行四边形叫做菱形；‎ 判定方法1：四条边都相等的四边形是菱形；‎ 判定方法2：对角线互相垂直的平行四边形是菱形．‎ ‎ 3.矩形 ‎ ①定义：有一个内角是直角的平行四边形是矩形．‎ ‎ ②性质：具有平行四边形的一切性质；矩形的四个角都是直角；矩形的对角线相等；矩形既是轴对称图形，又是中心对称图形。‎ ‎ ③判定方法 定义：有一个角是直角的平行四边形是矩形；‎ 判定方法1：有三个角是直角的四边形是矩形；‎ 判定方法2：对角线相等的平行四边形是矩形．‎ ‎ 第二部分 精讲点拨 ‎ 考点1.平行四边形的性质 ‎ 【例1】如图，在平行四边形ABCD中，DB=DC.，CEBD于E，则 ． ‎ ‎ 变式1 □ABCD中，CE⊥AB，垂足为E，如果∠A=115°，则∠BCE= . ‎ ‎ 变式2 在平行四边形ABCD中，点A1.A2.A3.A4和C1.C2.C3.C4分别AB和CD的五等分点,点B1.B2和D1.D2分别是BC和DA的三等分点,已知四边形A4 B2 C4 D2的面积为1,则平行四边形ABCD面积为（ ）‎ A.2 B. C. 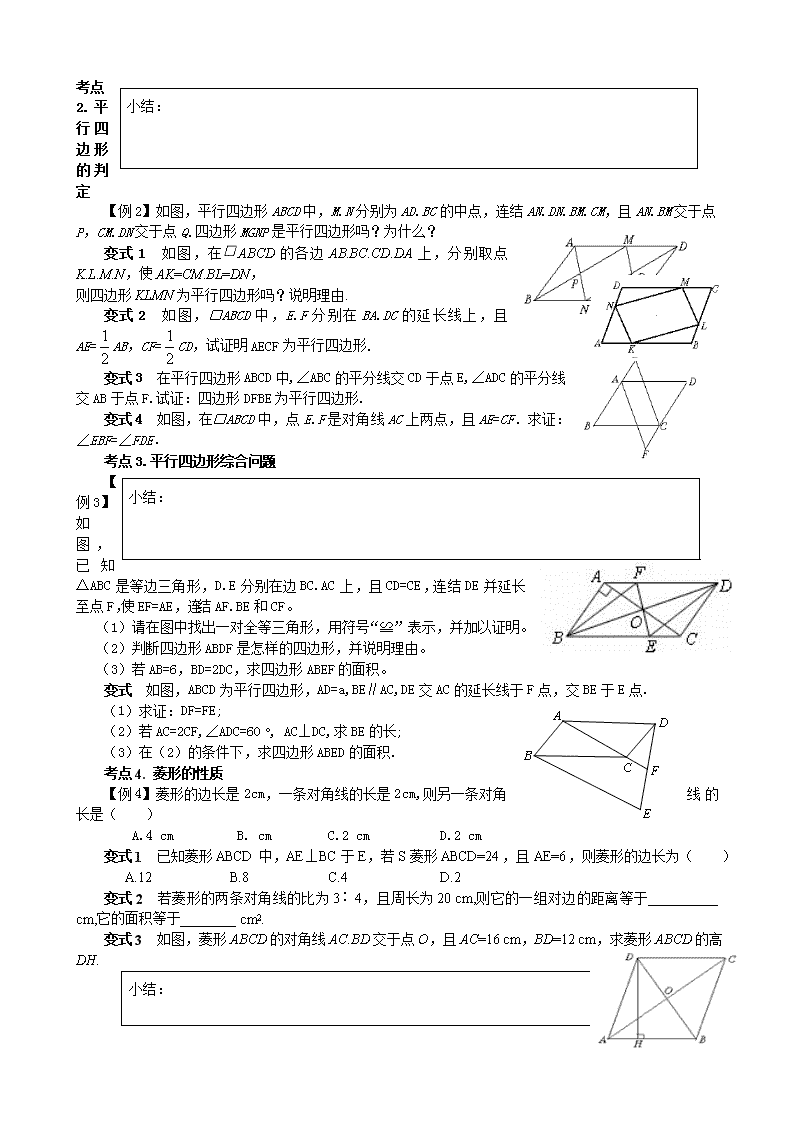D.15‎ 变式3 如图，□ABCD中，已知AD＝8㎝， AB＝6㎝， DE平分∠ADC交BC边于点E，则BE等于（ ） ‎ ‎ A.2cm B.4cm C.6cm D.8cm 变式4 如图，已知平分，，，则 ．‎ 变式5 如图，已知：平行四边形ABCD中，的平分线交边于，的平分线 ‎ 交于，交于．求证：．‎ 小结：‎ 考点2.平行四边形的判定 ‎ 【例2】如图，平行四边形ABCD中，M.N分别为AD.BC的中点，连结AN.DN.BM.CM，且AN.BM交于点P，CM.DN交于点Q.四边形MGNP是平行四边形吗？为什么？‎ 变式1 如图，在ABCD的各边AB.BC.CD.DA上，分别取点K.L.M.N，使AK=CM.BL=DN， ‎ 则四边形KLMN为平行四边形吗？说明理由.‎ ‎ 变式2 如图，□ABCD中，E.F分别在BA.DC的延长线上，且AE=AB，CF=CD，试证明AECF为平行四边形.‎ ‎ 变式3 在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试证：四边形DFBE为平行四边形.‎ ‎ 变式4 如图，在□ABCD中，点E.F是对角线AC上两点，且AE=CF．求证：∠EBF=∠FDE．‎ 小结：‎ ‎ 考点3.平行四边形综合问题 ‎【例3】如图，已知△ABC是等边三角形，D.E分别在边BC.AC上，且CD=CE，连结DE并延长至点F，使EF=AE，连结AF.BE和CF。‎ ‎ （1）请在图中找出一对全等三角形，用符号“≌”表示，并加以证明。‎ ‎ （2）判断四边形ABDF是怎样的四边形，并说明理由。‎ ‎ （3）若AB=6，BD=2DC，求四边形ABEF的面积。‎ ‎ 变式 如图，ABCD为平行四边形，AD=a,BE∥AC,DE交AC的延长线于F点，交BE于E点.‎ ‎ （1）求证：DF=FE; ‎ ‎ （2）若AC=2CF,∠ADC=60 o, AC⊥DC,求BE的长;‎ ‎ （3）在（2）的条件下，求四边形ABED的面积.‎ ‎ 考点4. 菱形的性质 ‎【例4】菱形的边长是2 cm，一条对角线的长是2 cm,则另一条对角线的长是（ ）‎ ‎ A.4 cm B. cm C.2 cm D.2 cm ‎ 变式1 已知菱形ABCD中，AE⊥BC于E，若S菱形ABCD=24，且AE=6，则菱形的边长为（ ）‎ ‎　　 A.12 B.8 C.4 D.2‎ ‎ 变式2 若菱形的两条对角线的比为3∶4，且周长为20 cm,则它的一组对边的距离等于__________ cm,它的面积等于________ cm2.‎ 变式3 如图，菱形ABCD的对角线AC.BD交于点O，且AC=16 cm，BD=12 cm，求菱形ABCD的高DH.‎ 小结：‎ ‎ 考点5. 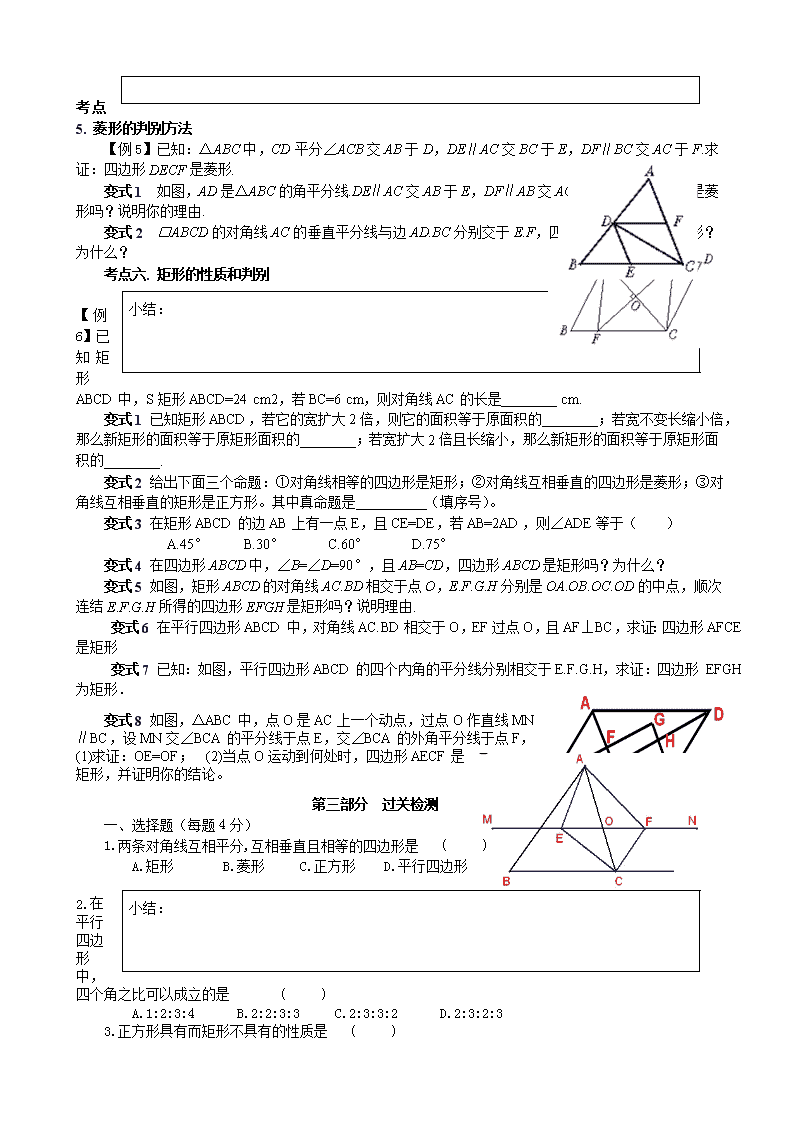菱形的判别方法 ‎【例5】已知：△ABC中，CD平分∠ACB交AB于D，DE∥AC交BC于E，DF∥BC交AC于F.求证：四边形DECF是菱形.‎ ‎ 变式1 如图，AD是△ABC的角平分线.DE∥AC交AB于E，DF∥AB交AC于F.四边形AEDF是菱形吗？说明你的理由.‎ 变式2 □ABCD的对角线AC的垂直平分线与边AD.BC分别交于E.F，四边形AFCE是否是菱形？为什么？‎ 小结：‎ ‎ 考点六. 矩形的性质和判别 ‎ 【例6】已知矩形ABCD中，S矩形ABCD=24 cm2，若BC=6 cm，则对角线AC的长是________ cm.‎ ‎ 变式1 已知矩形ABCD，若它的宽扩大2倍，则它的面积等于原面积的________；若宽不变长缩小倍，那么新矩形的面积等于原矩形面积的________；若宽扩大2倍且长缩小，那么新矩形的面积等于原矩形面积的________.‎ ‎ 变式2 给出下面三个命题：①对角线相等的四边形是矩形；②对角线互相垂直的四边形是菱形；③对角线互相垂直的矩形是正方形。其中真命题是 （填序号）。‎ ‎ 变式3 在矩形ABCD的边AB上有一点E，且CE=DE，若AB=2AD，则∠ADE等于（ ）‎ ‎ A.45° B.30° C.60° D.75°‎ ‎ 变式4 在四边形ABCD中，∠B=∠D=90°，且AB=CD，四边形ABCD是矩形吗？为什么？‎ ‎ 变式5 如图，矩形ABCD的对角线AC.BD相交于点O，E.F.G.H分别是OA.OB.OC.OD的中点，顺次连结E.F.G.H所得的四边形EFGH是矩形吗？说明理由.‎ ‎ 变式6 在平行四边形ABCD中，对角线AC.BD相交于O，EF过点O，且AF⊥BC，求证：四边形AFCE是矩形 ‎ 变式7 已知：如图，平行四边形ABCD的四个内角的平分线分别相交于E.F.G.H，求证：四边形 EFGH为矩形．‎ ‎ 变式8 如图，△ABC中，点O是AC上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F， (1)求证：OE=OF； (2)当点O运动到何处时，四边形AECF是矩形，并证明你的结论。‎ 小结：‎ ‎ 第三部分 过关检测 ‎ 一、选择题（每题4分）‎ ‎ 1.两条对角线互相平分,互相垂直且相等的四边形是 ( )‎ ‎ A.矩形 B.菱形 C.正方形 D.平行四边形 ‎ 2.在平行四边形中，四个角之比可以成立的是 ( )‎ ‎ A.1:2:3:4 B.2:2:3:3 C.2:3:3:2 D.2:3:2:3 ‎ ‎ 3.正方形具有而矩形不具有的性质是 ( )‎ ‎ A.四个角都是直角 B.对角线相等 C.对角线互相平分 D.对角线互相垂直 ‎ 4.下列图形中，不是中心对称图形的是（ ）‎ ‎ A.线段 B.矩形 C.等腰梯形 D.正方形 ‎ 5.内角和是外角和3倍的的多边形是（ ）边形 ‎ A.4 B.4 C.7 D.8‎ ‎ 6.菱形的周长是，两对角线的比为3∶4，则对角线的长分别是 ( )‎ ‎ A.12㎝，16㎝ B.6㎝，8㎝ C.3㎝，4㎝ D.24㎝，32㎝ ‎ 7.如图，等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，△DEC的周长是 ( )‎ ‎ A.3 B.12 C.15 D.19‎ ‎3cm ‎3cm ‎ 8.如图，把长为8cm的矩形沿虚线对折，按图中的虚线剪出一个直角梯形，打开得到一个等腰梯形，剪掉部分的面积为6cm2，则打开后梯形的周长是（ ）。‎ ‎ A.（10+）cm 　B.（10+）cm 　　 C.20cm D.22cm ‎ 二、填空(每题4分)‎ ‎ 9.若一个多边形的每一个外角都等于30°,则它的内角和等 ‎10.如图1，在□ABCD中，则图中全等三角形共有_______对，AB= , BC= . ‎ ‎ 图1 图2 图3‎ ‎11.如图2，菱形中，∠ADC=120°，AB=10,则,菱形的面积=。‎ ‎12.如图3，等腰梯形ABCD中，,，则梯形ABCD的周长= ，梯形ABCD的面积 ‎ 13.如图，已知矩形ABCD中，AB=CD，AB=5,E为BC边上的一点,∠EBC=30°,‎ 对角线的长为，则BE的长为 。‎ ‎ 三、解答题 ‎ 14.（本题8分）如图，如图，在□ABCD中，AC交BD于点O，点E.点F分别是OA.OC的中点，请判 断线段BE.DF的关系，并证明你的结论。‎ ‎ 15.（本题8分）如图，等腰△ABC中，D是BC边上的一点，DE∥AC，DF∥AB，通过观察分析线段DE，DF，AB三者之间有什么关系？试说明你的结论成立的理由 ‎16.（本题8分）如图，已知矩形ABCD中，对角线AC、BD相交于点O，AE⊥BD，垂足为E，‎ ‎∠DAE∶∠BAE＝3∶1，求∠EAC的度数。‎ ‎17.（本题10分）如图，等腰梯形中，AD∥BC，AB=DC，∠B＝600，对角线AC平分∠BCD，‎ AE∥DC,（1）试说明四边形AECD的形状，并说明理由；‎ ‎ （2）梯形周长为20cm，求BC的长 ‎18.（12分）如图, 在矩形ABCD中, 点E在AD上, EC平分.‎ ‎(1) 试判断的形状, 并说明理由;（4分）‎ ‎(2) 若AB=1, , 求BC的长;（4分）‎ ‎(3) 在原图中画, 使它与关于CE的中点O成中心对称(不写作法), 此时四边形BCFE是什么特殊平行四边形? 请说明理由.（4分）‎ ‎19.（10分）选做题：不记入总分 在△ABC中，AB＝BC＝5，AC=6. △ECD是△ABC沿BC方向平移得到的，连接AE.AC和BE相交于点O.‎ ‎ （1）判断四边形ABCE是怎样的四边形，说明理由； ‎ ‎ （2）如图2，P是线段BC上一动点（图2），（不与点B.C重合），连接PO并延长交线段AB于点Q，QR⊥BD，垂足为点R.四边形PQED的面积是否随点P的运动而发生变化？若变化，请说明理由；若不变，求出四边形PQED的面积；‎