2012年珠海中考数学试卷 9页

‎2012年珠海市初中毕业生学业考试 数 学 一、选择题（本大题5小题，每小题3分，共15分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.‎ ‎1．2的倒数是 A．2 B．－2 C． D．‎ ‎2．计算的结果为 A． B． C． D．‎ ‎3．某同学对甲、乙、丙、丁四个市场二月份每天的白菜价格进行调查，计算后发现这个月四个市场的价格平均值相同、方差分别为.二月份白菜价格最稳定的市场是 A．甲 B．乙 C．丙 D．丁 ‎4、下列图形中不是中心对称图形的是 ‎ A.矩形 B.菱形 C.平行四边形 D.正五边形 ‎5．如果一个扇形的半径是1，弧长是，那么此扇形的圆心角的大小为 A．30°B．45°C．60°D．90°‎ 二、填空题（本大题5小题，每小题4分，共20分）请将下列各题的正确答案填写在答题卡相应的位置上.‎ ‎6．计算 .‎ ‎7．使有意义的取值范围是 .‎ ‎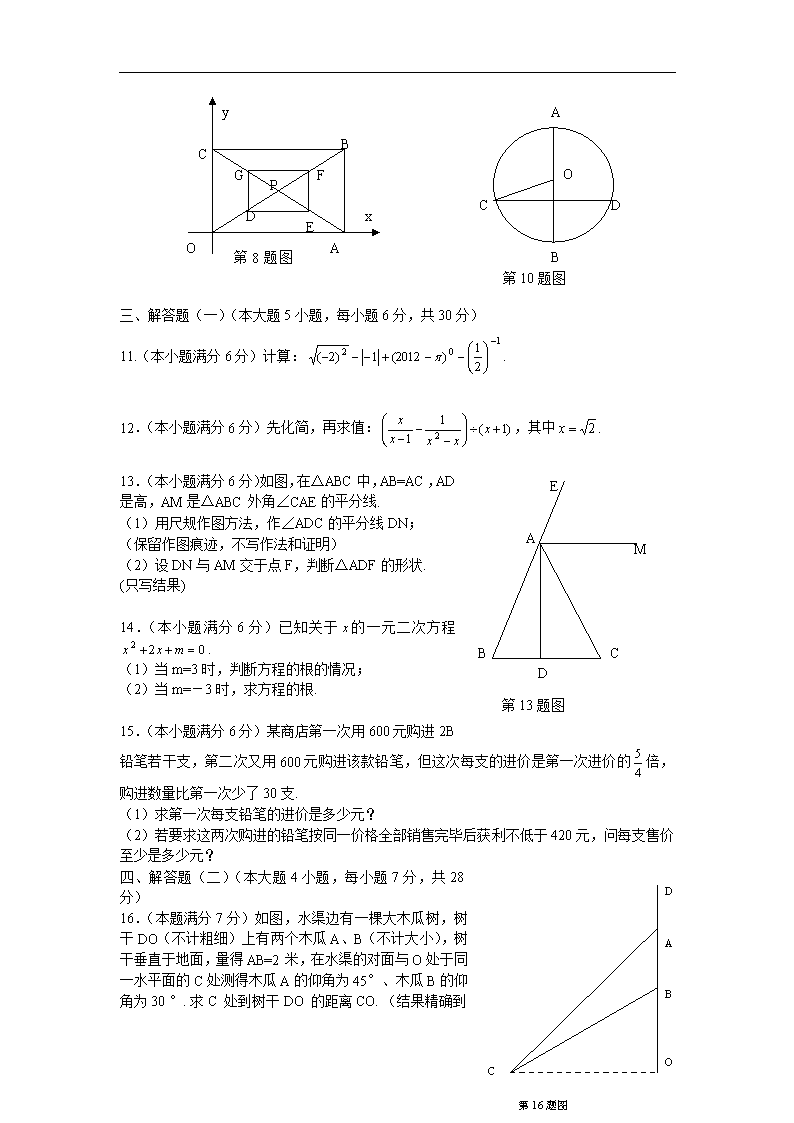8．如图，矩形OABC的顶点A、C分别在轴、轴正半轴上，B点坐标为（3，2），OB与AC交于点P，D、E、F、G分别是线段OP、AP、BP、CP的中点，则四边形DEFG的周长为 .‎ ‎9．不等式组的解集是 .‎ ‎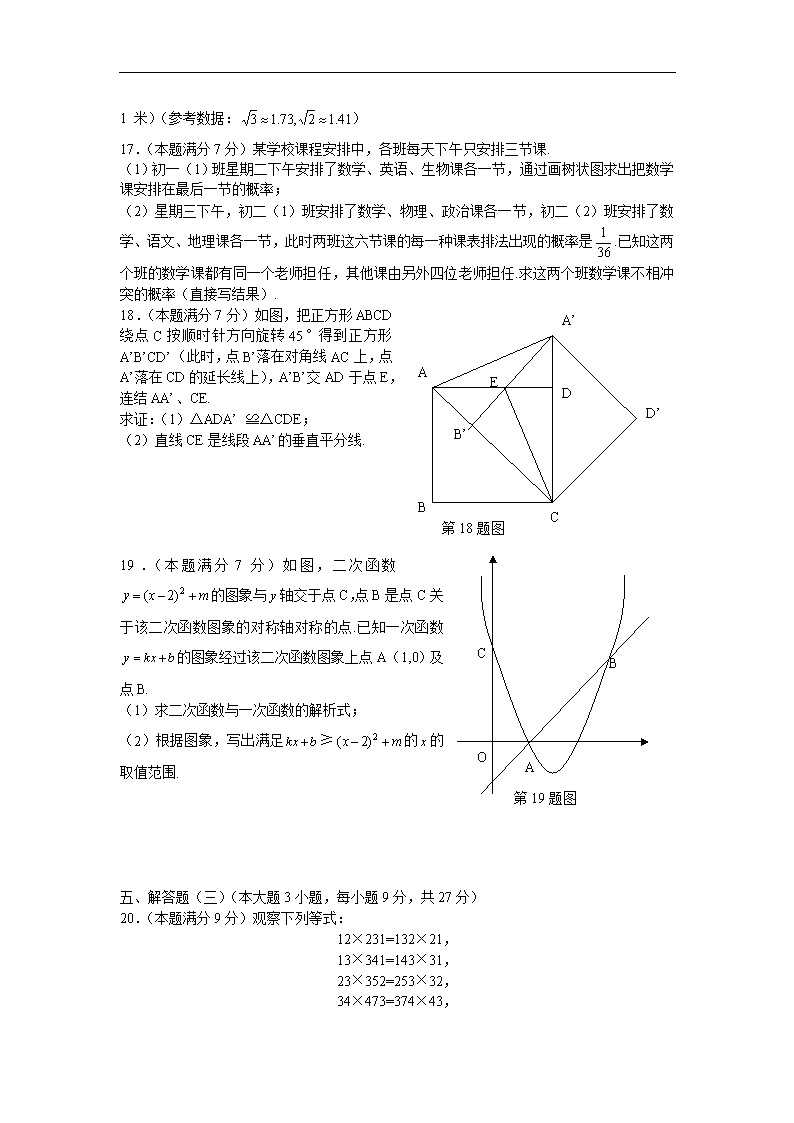10．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=26，CD=24，那么sin∠OCE= .‎ O C A B D E F G P x y 第8题图=‎ ‎ ‎O A B C D 第10题图 三、解答题（一）（本大题5小题，每小题6分，共30分）‎ ‎11.（本小题满分6分）计算：.‎ ‎12．（本小题满分6分）先化简，再求值：，其中.‎ A B C D E M 第13题图 ‎13．（本小题满分6分）如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线.‎ ‎（1）用尺规作图方法，作∠ADC的平分线DN；‎ ‎（保留作图痕迹，不写作法和证明）‎ ‎（2）设DN与AM交于点F，判断△ADF的形状.‎ ‎(只写结果)‎ ‎14．（本小题满分6分）已知关于的一元二次方程.‎ ‎（1）当m=3时，判断方程的根的情况；‎ ‎（2）当m=－3时，求方程的根.‎ ‎15．（本小题满分6分）某商店第一次用600元购进2B铅笔若干支，第二次又用600元购进该款铅笔，但这次每支的进价是第一次进价的倍，购进数量比第一次少了30支.‎ ‎（1）求第一次每支铅笔的进价是多少元？‎ ‎（2）若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元，问每支售价至少是多少元？‎ C O D A B 第16题图 四、解答题（二）（本大题4小题，每小题7分，共28分）‎ ‎16．（本题满分7分）如图，水渠边有一棵大木瓜树，树干DO（不计粗细）上有两个木瓜A、B（不计大小），树干垂直于地面，量得AB=2米，在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°‎ ‎.求C处到树干DO的距离CO.（结果精确到1米）（参考数据：）‎ ‎17．（本题满分7分）某学校课程安排中，各班每天下午只安排三节课.‎ ‎（1）初一（1）班星期二下午安排了数学、英语、生物课各一节，通过画树状图求出把数学课安排在最后一节的概率；‎ ‎（2）星期三下午，初二（1）班安排了数学、物理、政治课各一节，初二（2）班安排了数学、语文、地理课各一节，此时两班这六节课的每一种课表排法出现的概率是.已知这两个班的数学课都有同一个老师担任，其他课由另外四位老师担任.求这两个班数学课不相冲突的概率（直接写结果）.‎ A B C D A’‎ B’‎ D’‎ E 第18题图 ‎18．（本题满分7分）如图，把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A’B’CD’（此时，点B’落在对角线AC上，点A’落在CD的延长线上），A’B’交AD于点E，连结AA’、CE.‎ 求证：（1）△ADA’ ≌△CDE；‎ ‎（2）直线CE是线段AA’的垂直平分线.‎ A B C O 第19题图 ‎19．（本题满分7分）如图，二次函数的图象与轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数的图象经过该二次函数图象上点A（1,0）及点B.‎ ‎（1）求二次函数与一次函数的解析式；‎ ‎（2）根据图象，写出满足≥的的取值范围.‎ 五、解答题（三）（本大题3小题，每小题9分，共27分）‎ ‎20．（本题满分9分）观察下列等式：‎ ‎12×231=132×21，‎ ‎13×341=143×31，‎ ‎23×352=253×32，‎ ‎34×473=374×43，‎ ‎62×286=682×26，‎ ‎……‎ 以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”.‎ ‎（1）根据上述各式反映的规律填空，使式子称为“数字对称等式”：‎ ‎①52× ＝ ×25；‎ ‎② ×396＝693× .‎ ‎（2）设这类等式左边两位数的十位数字为，个位数字为，且2≤≤9，写出表示“数字对称等式”一般规律的式子（含、），并证明.‎ ‎21．（本题满分9分）已知，AB是⊙O的直径，点P在弧AB上（不含点A、B），把△AOP沿OP对折，点A的对应点C恰好落在⊙O上.‎ ‎（1）当P、C都在AB上方时（如图1），判断PO与BC的位置关系（只回答结果）；‎ ‎（2）当P在AB上方而C在AB下方时（如图2），（1）中结论还成立吗？证明你的结论；‎ ‎（3）当P、C都在AB上方时（如图3），过C点作CD⊥直线AP于D，且CD是⊙O的切线，证明：AB=4PD.‎ 第21题图3‎ 第21题图2‎ 第21题图1‎ ‎22．（本题满分9分）如图，在等腰梯形ABCD中，ABDC，AB=，DC=，高CE=，对角线AC、BD交于H，平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移，分别交等腰梯形ABCD的边于M、N和R、Q，分别交对角线AC于F、G；当直线RQ到达点C时，，两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的图形面积为、被直线RQ扫过的图形面积为，若直线MN平移的速度为1单位/秒，直线RQ平移的速度为2单位/秒，设两直线移动的时间为秒.‎ ‎（1）填空：∠AHB= ；AC= ；‎ ‎（2）若，求；‎ ‎（3）设，求的变化范围.‎