2009年湖北仙桃天门潜江江汉油田中考数学试题 4页

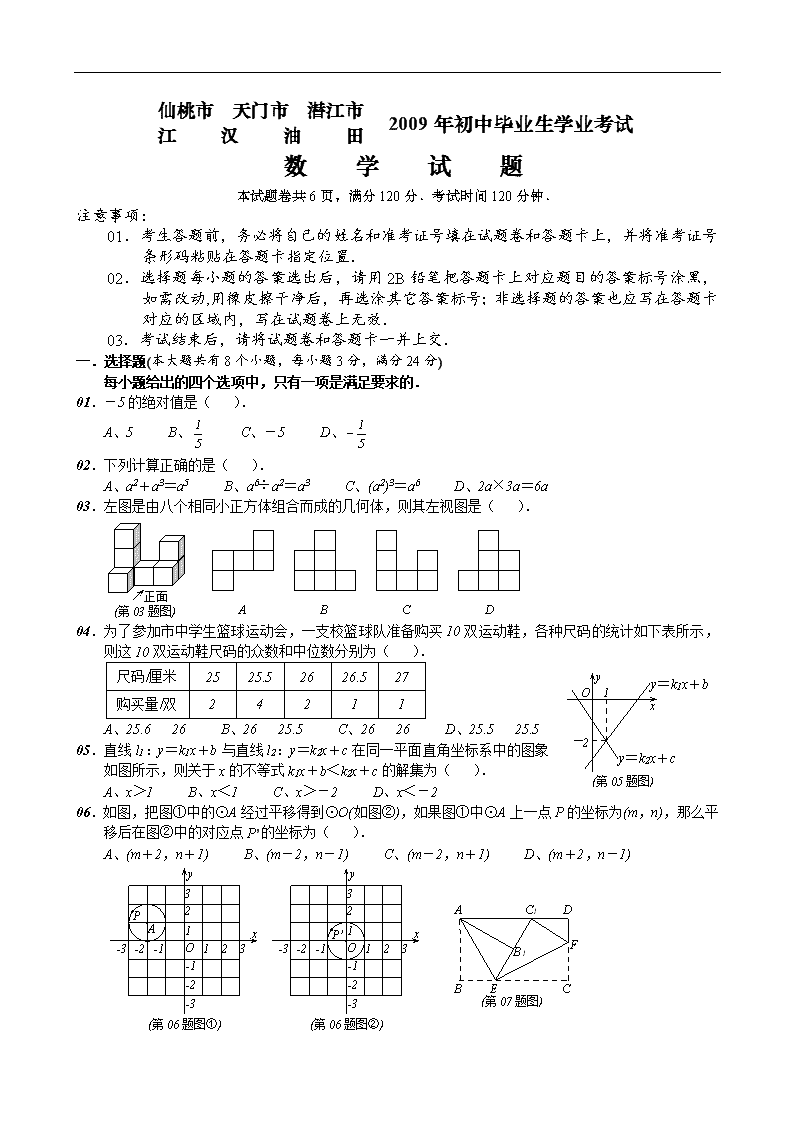
2009 年初中毕业生学业考试 数 学 试 题 本试题卷共 6 页，满分 120 分．考试时间 120 分钟． 注意事项： 01．考生答题前，务必将自己的姓名和准考证号填在试题卷和答题卡上，并将准考证号 条形码粘贴在答题卡指定位置． 02．选择题每小题的答案选出后，请用 2B 铅笔把答题卡上对应题目的答案标号涂黑， 如需改动,用橡皮擦干净后，再选涂其它答案标号；非选择题的答案也应写在答题卡 对应的区域内，写在试题卷上无效． 03．考试结束后，请将试题卷和答题卡一并上交． 一．选择题(本大题共有 8 个小题，每小题 3 分，满分 24 分) 每小题给出的四个选项中，只有一项是满足要求的． 01．－5 的绝对值是（ ）． A、5 B、 5 1 C、－5 D、 5 1 02．下列计算正确的是（ ）． A、a2＋a3＝a5 B、a6÷a2＝a3 C、(a2)3＝a6 D、2a×3a＝6a 03．左图是由八个相同小正方体组合而成的几何体，则其左视图是（ ）． 04．为了参加市中学生篮球运动会，一支校篮球队准备购买 10 双运动鞋，各种尺码的统计如下表所示， 则这 10 双运动鞋尺码的众数和中位数分别为（ ）． 尺码/厘米 25 25.5 26 26.5 27 购买量/双 2 4 2 1 1 A、25.6 26 B、26 25.5 C、26 26 D、25.5 25.5 05．直线 l1：y＝k1x＋b 与直线 l2：y＝k2x＋c 在同一平面直角坐标系中的图象 如图所示，则关于 x 的不等式 k1x＋b＜k2x＋c 的解集为（ ）． A、x＞1 B、x＜1 C、x＞－2 D、x＜－2 06．如图，把图①中的⊙A 经过平移得到⊙O(如图②)，如果图①中⊙A 上一点 P 的坐标为(m，n)，那么平 移后在图②中的对应点 P’的坐标为（ ）． A、(m＋2，n＋1) B、(m－2，n－1) C、(m－2，n＋1) D、(m＋2，n－1) 仙桃市 天门市 潜江市 江 汉 油 田 正面 (第 03 题图) A B C D O 1 x y (第 05 题图) －2 y＝k2x＋c y＝k1x＋b y -1 -2 -3 2 3 1 -3 -2 -1 O 1 2 3 xP’ (第 06 题图②) y A -1 -2 -3 2 3 1 -3 -2 -1 O 1 2 3 x P (第 06 题图①) A B C D E C1 B1 F (第 07 题图) 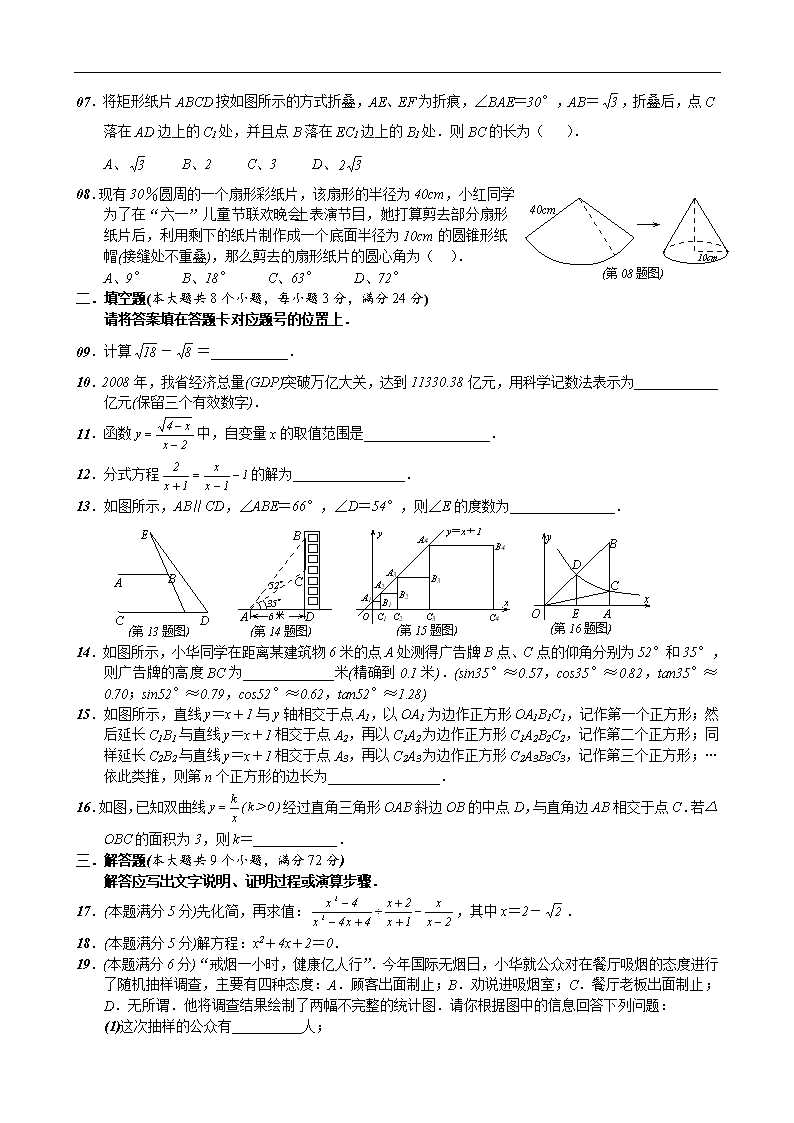07．将矩形纸片 ABCD 按如图所示的方式折叠，AE、EF 为折痕，∠BAE＝30°，AB＝ 3 ，折叠后，点 C 落在 AD 边上的 C1 处，并且点 B 落在 EC1 边上的 B1 处．则 BC 的长为（ ）． A、 3 B、2 C、3 D、 32 08．现有 30％圆周的一个扇形彩纸片，该扇形的半径为 40cm，小红同 学为了在“六一”儿童节联欢晚会上表演节目，她打算剪去部分扇 形纸片后，利用剩下的纸片制作成一个底面半径为 10cm 的圆锥形 纸帽(接缝处不重叠)，那么剪去的扇形纸片的圆心角为（ ）． A、9° B、18° C、63° D、72° 二．填空题(本大题共 8 个小题，每小题 3 分，满分 24 分) 请将答案填在答题卡对应题号的位置上． 09．计算 18 － 8 ＝___________． 10．2008 年，我省经济总量(GDP)突破万亿大关，达到 11330.38 亿元，用科学记数法表示为____________ 亿元(保留三个有效数字)． 11．函数 2x x4y   中，自变量 x 的取值范围是__________________． 12．分式方程 11x x 1x 2  的解为________________． 13．如图所示，AB∥CD，∠ABE＝66°，∠D＝54°，则∠E 的度数为_______________． 14．如图所示，小华同学在距离某建筑物 6 米的点 A 处测得广告牌 B 点、C 点的仰角分别为 52°和 35°， 则广告牌的高度 BC 为_____________米(精确到 0.1 米)．(sin35°≈0.57，cos35°≈0.82，tan35°≈0.70； sin52°≈0.79，cos52°≈0.62，tan52°≈1.28) 15．如图所示，直线 y＝x＋1 与 y 轴相交于点 A1，以 OA1 为边作正方形 OA1B1C1，记作第一个正方形；然 后延长 C1B1 与直线 y＝x＋1 相交于点 A2，再以 C1A2 为边作正方形 C1A2B2C2，记作第二个正方形；同 样延长 C2B2 与直线 y＝x＋1 相交于点 A3，再以 C2A3 为边作正方形 C2A3B3C3，记作第三个正方形；… 依此类推，则第 n 个正方形的边长为________________． 16．如图，已知双曲线 )0k(x ky ＞ 经过直角三角形 OAB 斜边 OB 的中点 D，与直角边 AB 相交于点 C．若 △OBC 的面积为 3，则 k＝____________． 三．解答题(本大题共 9 个小题，满分 72 分) 解答应写出文字说明、证明过程或演算步骤． 17．(本题满分 5 分)先化简，再求值： 2x x 1x 2x 4x4x 4x 2 2    ，其中 x＝2－ 2 ． 18．(本题满分 5 分)解方程：x2＋4x＋2＝0． 19．(本题满分 6 分)“戒烟一小时，健康亿人行”．今年国际无烟日，小华就公众对在餐厅吸烟的态度进行 了随机抽样调查，主要有四种态度：A．顾客出面制止；B．劝说进吸烟室；C．餐厅老板出面制止； D．无所谓．他将调查结果绘制了两幅不完整的统计图．请你根据图中的信息回答下列问题： (1)这次抽样的公众有__________人； 40cm 10cm (第 08 题图) A B C D E (第 13 题图) A B C D6 米 52° 35° (第 14 题图) A1 A2 A3 A4 B1 B2 B3 B4 x y＝x＋1 O C1 C2 C3 C4 (第 15 题图) y A B C D E y x O (第 16 题图) (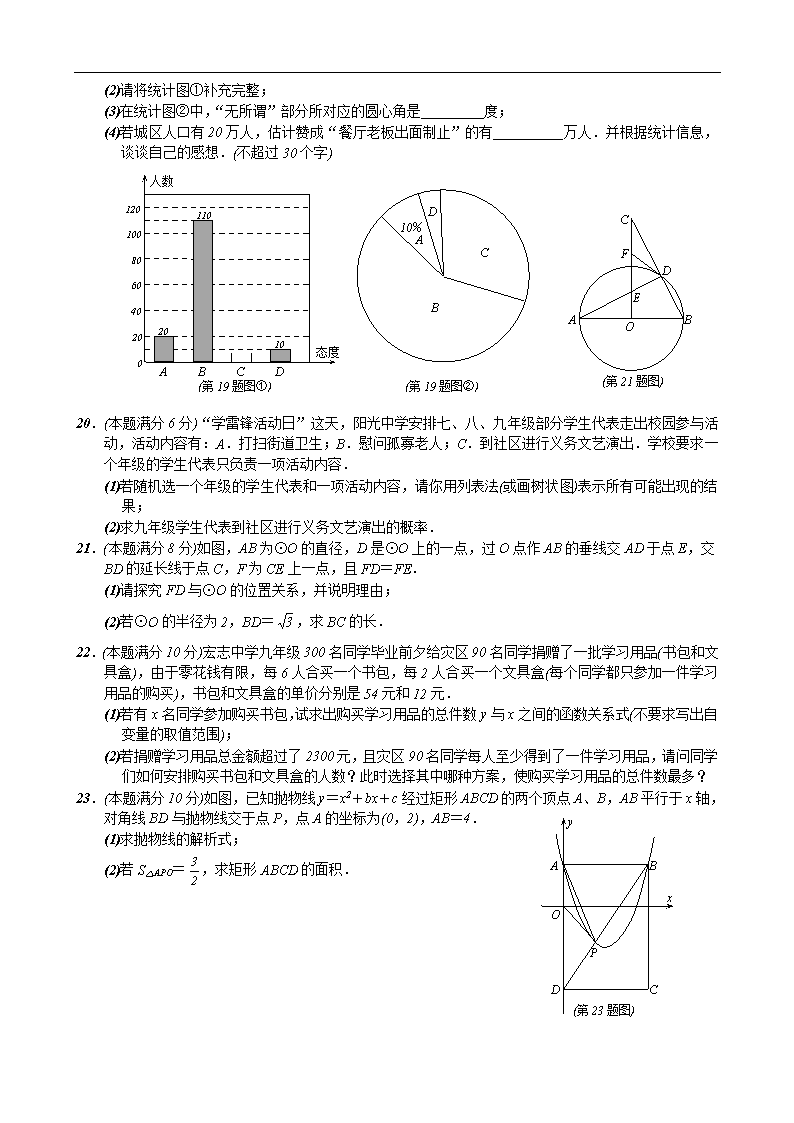2)请将统计图①补充完整； (3)在统计图②中，“无所谓”部分所对应的圆心角是_________度； (4)若城区人口有 20 万人，估计赞成“餐厅老板出面制止”的有__________万人．并根据统计信息， 谈谈自己的感想．(不超过 30 个字) 20．(本题满分 6 分)“学雷锋活动日”这天，阳光中学安排七、八、九年级部分学生代表走出校园参与活 动，活动内容有：A．打扫街道卫生；B．慰问孤寡老人；C．到社区进行义务文艺演出．学校要求一 个年级的学生代表只负责一项活动内容． (1)若随机选一个年级的学生代表和一项活动内容，请你用列表法(或画树状图)表示所有可能出现的结 果； (2)求九年级学生代表到社区进行义务文艺演出的概率． 21．(本题满分 8 分)如图，AB 为⊙O 的直径，D 是⊙O 上的一点，过 O 点作 AB 的垂线交 AD 于点 E，交 BD 的延长线于点 C，F 为 CE 上一点，且 FD＝FE． (1)请探究 FD 与⊙O 的位置关系，并说明理由； (2)若⊙O 的半径为 2，BD＝ 3 ，求 BC 的长． 22．(本题满分 10 分)宏志中学九年级 300 名同学毕业前夕给灾区 90 名同学捐赠了一批学习用品(书包和文 具盒)，由于零花钱有限，每 6 人合买一个书包，每 2 人合买一个文具盒(每个同学都只参加一件学习 用品的购买)，书包和文具盒的单价分别是 54 元和 12 元． (1)若有 x 名同学参加购买书包，试求出购买学习用品的总件数 y 与 x 之间的函数关系式(不要求写出自 变量的取值范围)； (2)若捐赠学习用品总金额超过了 2300 元，且灾区 90 名同学每人至少得到了一件学习用品，请问同学 们如何安排购买书包和文具盒的人数？此时选择其中哪种方案，使购买学习用品的总件数最多？ 23．(本题满分 10 分)如图，已知抛物线 y＝x2＋bx＋c 经过矩形 ABCD 的两个顶点 A、B，AB 平行于 x 轴， 对角线 BD 与抛物线交于点 P，点 A 的坐标为(0，2)，AB＝4． (1)求抛物线的解析式； (2)若 S△APO＝ 2 3 ，求矩形 ABCD 的面积． (第 19 题图①) 100 120 0 20 10 60 80 40 110 人数 20 A B C D 态度 A B C D 10％ (第 19 题图②) A B C D E F (第 21 题图) O A B CD y P x O (第 23 题图) 24．(本题满分 10 分)如图所示，在△ABC 中，D、E 分别是 AB、AC 上的点，DE∥BC，如图①，然后将 △ADE 绕 A 点顺时针旋转一定角度，得到图②，然后将 BD、CE 分别延长至 M、N，使 DM＝ 2 1 BD， EN＝ 2 1 CE，得到图③，请解答下列问题： (1)若 AB＝AC，请探究下列数量关系： ①在图②中，BD 与 CE 的数量关系是________________； ②在图③中，猜想 AM 与 AN 的数量关系、∠MAN 与∠BAC 的数量关系，并证明你的猜想； (2)若 AB＝k·AC(k＞1)，按上述操作方法，得到图④，请继续探究：AM 与 AN 的数量关系、∠MAN 与∠BAC 的数量关系，直接写出你的猜想，不必证明． 25．(本题满分 12 分)如图，直角梯形 ABCD 中，AD∥BC，∠ABC＝90°，已知 AD＝AB＝3，BC＝4，动点 P 从 B 点出发，沿线段 BC 向点 C 作匀速运动；动点 Q 从点 D 出发，沿线段 DA 向点 A 作匀速运动．过 Q 点垂直于 AD 的射线交 AC 于点 M，交 BC 于点 N．P、Q 两点同时出发，速度都为每秒 1 个单位长 度．当 Q 点运动到 A 点，P、Q 两点同时停止运动．设点 Q 运动的时间为 t 秒． (1)求 NC，MC 的长(用 t 的代数式表示)； (2)当 t 为何值时，四边形 PCDQ 构成平行四边形？ (3)是否存在某一时刻，使射线 QN 恰好将△ABC 的面积和周长同时平分？若存在，求出此时 t 的值； 若不存在，请说明理由； (4)探究：t 为何值时，△PMC 为等腰三角形？ 答卷完后，请回过头来检查一遍，可要仔细哟！ AB C D E (第 24 题图①) (第 24 题图②) B C D A E AB C D E (第 24 题图③) N M AB C D E (第 24 题图④) N M A B C DQ M NP (第 25 题图)