详解版全国120份中考试卷分类汇编平面直角坐标系与点的坐标 22页

平面直角坐标系与点的坐标 一、选择题 ‎1.（2014•孝感，第9题3分）如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（　　）‎ ‎　‎ A．‎ ‎（2，10）‎ B．‎ ‎（﹣2，0）‎ C．‎ ‎（2，10）或（﹣2，0）‎ D．‎ ‎（10，2）或（﹣2，0）‎ 考点：‎ 坐标与图形变化－旋转．‎ 分析：‎ 分顺时针旋转和逆时针旋转两种情况讨论解答即可．‎ 解答：‎ 解：∵点D（5，3）在边AB上，‎ ‎∴BC=5，BD=5﹣3=2，‎ ‎①若顺时针旋转，则点D′在x轴上，OD′=2，‎ 所以，D′（﹣2，0），‎ ‎②若逆时针旋转，则点D′到x轴的距离为10，到y轴的距离为2，‎ 所以，D′（2，10），‎ 综上所述，点D′的坐标为（2，10）或（﹣2，0）．‎ 故选C．‎ 点评：‎ 本题考查了坐标与图形变化﹣旋转，正方形的性质，难点在于分情况讨论．‎ ‎2．（2014·台湾，第9题3分）如图，坐标平面上，△ABC与△DEF全等，其中A、B、C的对应顶点分别为D、E、F，且AB＝BC＝5．若A点的坐标为(﹣3，1)，B、C两点在方程式y＝﹣3的图形上，D、E两点在y轴上，则F点到y轴的距离为何？(　　)‎ A．2 B．3 C．4 D．5‎ 分析：如图，作AH、CK、FP分别垂直BC、AB、DE于H、K、P．由AB＝BC，△ABC≌△DEF，就可以得出△AKC≌△CHA≌△DPF，就可以得出结论．‎ 解：如图，作AH、CK、FP分别垂直BC、AB、DE于H、K、P．‎ ‎∴∠DPF＝∠AKC＝∠CHA＝90°．‎ ‎∵AB＝BC，‎ ‎∴∠BAC＝∠BCA．‎ 在△AKC和△CHA中。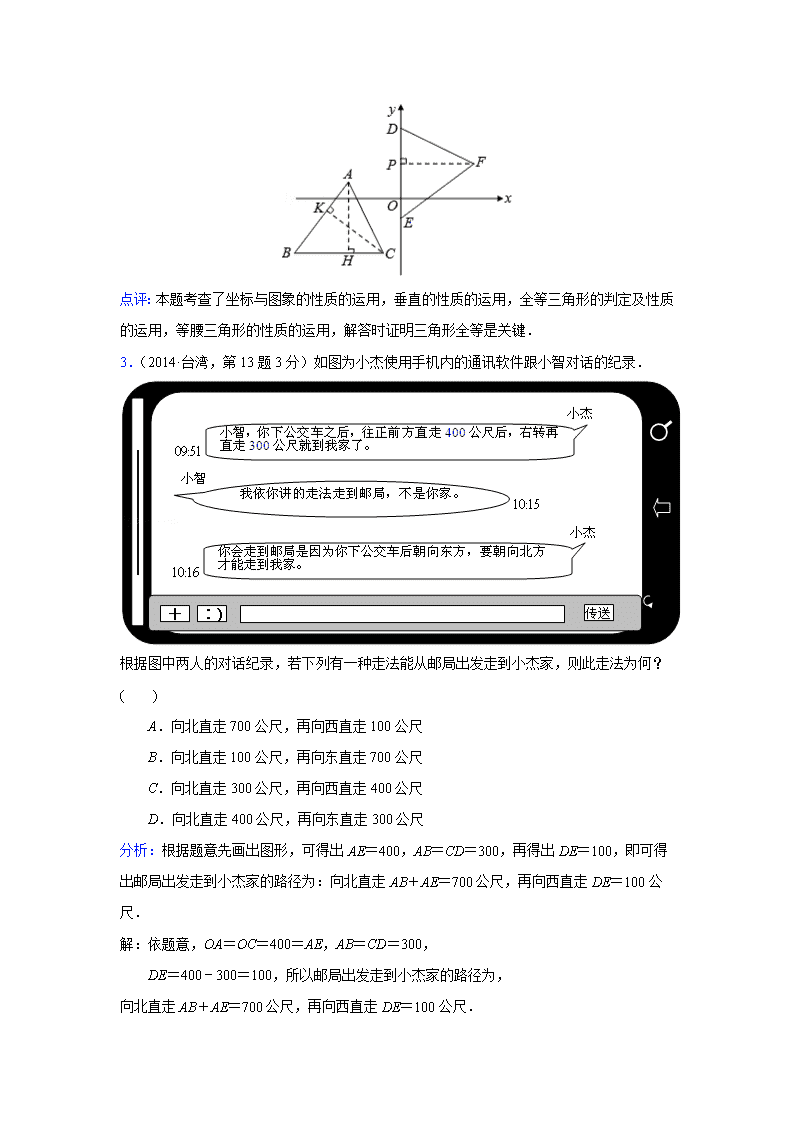‎ ‎∴△AKC≌△CHA(ASA)，‎ ‎∴KC＝HA．‎ ‎∵B、C两点在方程式y＝﹣3的图形上，且A点的坐标为(﹣3，1)，‎ ‎∴AH＝4．‎ ‎∴KC＝4．‎ ‎∵△ABC≌△DEF，‎ ‎∴∠BAC＝∠EDF，AC＝DF．‎ 在△AKC和△DPF中，‎ ‎∴△AKC≌△DPF(AAS)，‎ ‎∴KC＝PF＝4．‎ 故选C．‎ 点评：本题考查了坐标与图象的性质的运用，垂直的性质的运用，全等三角形的判定及性质的运用，等腰三角形的性质的运用，解答时证明三角形全等是关键．‎ ‎3．（2014·台湾，第13题3分）如图为小杰使用手机内的通讯软件跟小智对话的纪录．‎ 根据图中两人的对话纪录，若下列有一种走法能从邮局出发走到小杰家，则此走法为何？(　　)‎ A．向北直走700公尺，再向西直走100公尺 B．向北直走100公尺，再向东直走700公尺 C．向北直走300公尺，再向西直走400公尺 D．向北直走400公尺，再向东直走300公尺 分析：根据题意先画出图形，可得出AE＝400，AB＝CD＝300，再得出DE＝100，即可得出邮局出发走到小杰家的路径为：向北直走AB＋AE＝700公尺，再向西直走DE＝100公尺．‎ 解：依题意，OA＝OC＝400＝AE，AB＝CD＝300，‎ DE＝400﹣300＝100，所以邮局出发走到小杰家的路径为，‎ 向北直走AB＋AE＝700公尺，再向西直走DE＝100公尺．‎ 故选A．‎ 点评：本题考查了坐标确定位置，根据题意画出图形是解题的关键．‎ ‎4. （2014•益阳，第8题，4分）如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（﹣3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为（　　）‎ ‎（第1题图）‎ ‎　‎ A．‎ ‎1‎ B．‎ ‎1或5‎ C．‎ ‎3‎ D．‎ ‎5‎ 考点：‎ 直线与圆的位置关系；坐标与图形性质．‎ 分析：‎ 平移分在y轴的左侧和y轴的右侧两种情况写出答案即可．‎ 解答：‎ 解：当⊙P位于y轴的左侧且与y轴相切时，平移的距离为1；‎ 当⊙P位于y轴的右侧且与y轴相切时，平移的距离为5．‎ 故选B．‎ 点评：‎ 本题考查了直线与圆的位置关系，解题的关键是了解当圆与直线相切时，点到圆心的距离等于圆的半径．‎ ‎5. （2014•株洲，第8题，3分）在平面直角坐标系中，孔明做走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位…依此类推，第n步的走法是：当n能被3整除时，则向上走1个单位；当n被3除，余数为1时，则向右走1个单位；当n被3除，余数为2时，则向右走2个单位，当走完第100步时，棋子所处位置的坐标是（　　）‎ ‎　‎ A．‎ ‎（66，34）‎ B．‎ ‎（67，33）‎ C．‎ ‎（100，33）‎ D．‎ ‎（99，34）‎ 考点：‎ 坐标确定位置；规律型：点的坐标．‎ 分析：‎ 根据走法，每3步为一个循环组依次循环，且一个循环组内向右3个单位，向上1个单位，用100除以3，然后根据商和余数的情况确定出所处位置的横坐标与纵坐标即可．‎ 解答：‎ 解：由题意得，每3步为一个循环组依次循环，且一个循环组内向右3个单位，向上1个单位，‎ ‎∵100÷3=33余1，‎ ‎∴走完第100步，为第34个循环组的第1步，‎ 所处位置的横坐标为33×3+1=100，‎ 纵坐标为33×1=33，‎ ‎∴棋子所处位置的坐标是（100，33）．‎ 故选C．‎ 点评：‎ 本题考查了坐标确定位置，点的坐标的规律变化，读懂题目信息并理解每3步为一个循环组依次循环是解题的关键．‎ ‎6.（2014•呼和浩特，第3题3分）已知线段CD是由线段AB平移得到的，点A（﹣1，4）的对应点为C（4，7），则点B（﹣4，﹣1）的对应点D的坐标为（　　）‎ ‎　‎ A．‎ ‎（1，2）‎ B．‎ ‎（2，9）‎ C．‎ ‎（5，3）‎ D．‎ ‎（﹣9，﹣4）‎ 考点：‎ 坐标与图形变化－平移．‎ 分析：‎ 根据点A、C的坐标确定出平移规律，再求出点D的坐标即可．‎ 解答：‎ 解：∵点A（﹣1，4）的对应点为C（4，7），‎ ‎∴平移规律为向右5个单位，向上3个单位，‎ ‎∵点B（﹣4，﹣1），‎ ‎∴点D的坐标为（0，2）．‎ 故选A．‎ 点评：‎ 本题考查了坐标与图形变化﹣平移，平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．‎ ‎7.（2014•菏泽，第7题3分）若点M（x，y）满足（x+y）2=x2+y2﹣2，则点M 所在象限是（ ）‎ ‎　 A．第一象限或第三象限 B． 第二象限或第四象限 ‎　 C．第一象限或第二象限 D． 不能确定 考点：‎ 点的坐标；完全平方公式．‎ 分析：‎ 利用完全平方公式展开得到xy=﹣1，再根据异号得负判断出x、y异号，然后根据各象限内点的坐标特征解答．‎ 解答：‎ 解：∵（x+y）2=x2+2xy+y2，‎ ‎∴原式可化为xy=﹣1，‎ ‎∴x、y异号，‎ ‎∴点M（x，y）在第二象限或第四象限．‎ 故选B．‎ 点评：‎ 本题考查了点的坐标，求出x、y异号是解题的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．‎ ‎8.（2014•济宁，第9题3分）如图，将△ABC绕点C（0，1）旋转180°得到△A′B′C，设点A的坐标为（a，b），则点A′的坐标为（　　）‎ ‎　‎ A．‎ ‎（﹣a，﹣b）‎ B．‎ ‎（﹣a，﹣b﹣1）‎ C．‎ ‎（﹣a，﹣b+1）‎ D．‎ ‎（﹣a，﹣b+2）‎ 考点：‎ 坐标与图形变化－旋转．‎ 分析：‎ 设点A′的坐标是（x，y），根据旋转变换的对应点关于旋转中心对称，再根据中点公式列式求解即可．‎ 解答：‎ 解：根据题意，点A、A′关于点C对称，‎ 设点A′的坐标是（x，y），‎ 则=0，=1，‎ 解得x=﹣a，y=﹣b+2，‎ ‎∴点A的坐标是（﹣a，﹣b+2）．‎ 故选：D．‎ 点评：‎ 本题考查了利用旋转进行坐标与图形的变化，根据旋转的性质得出点A、A′关于点C成中心对称是解题的关键，还需注意中点公式的利用，也是容易出错的地方．‎ ‎9. (2014年湖北黄石) （2014•湖北黄石,第9题3分）正方形ABCD在直角坐标系中的位置如下图表示，将正方形ABCD绕点A顺时针方向旋转180°后，C点的坐标是（　　）‎ 第2题图 ‎　 A．（2，0） B． （3，0） C． （2，﹣1） D． （2，1）‎ 考点： 坐标与图形变化-旋转．‎ 分析： 正方形ABCD绕点A顺时针方向旋转180°后，C点的对应点与C一定关于A对称，A是对称点连线的中点，据此即可求解．‎ 解答： 解：AC=2，‎ 则正方形ABCD绕点A顺时针方向旋转180°后C的对应点设是C′，则AC′=AC=2，‎ 则OC′=3，‎ 故C′的坐标是（3，0）．‎ 故选B．‎ 点评： 本题考查了旋转的性质，理解C点的对应点与C一定关于A对称，A是对称点连线的中点是关键．‎ ‎10．（2014•乐山，第2题3分）如图，OA是北偏东30°方向的一条射线，若射线OB与射线OA垂直，则OB的方位角是（　　）‎ ‎　‎ A．‎ 北偏西30°‎ B．‎ 北偏西60°‎ C．‎ 东偏北30°‎ D．‎ 东偏北60°‎ 考点：‎ 方向角．.‎ 分析：‎ 根据垂直，可得∠AOB的度数，根据角的和差，可得答案．‎ 解答：‎ 解；若射线OB与射线OA垂直，‎ ‎∴∠AOB=90°，‎ ‎∠1=60°，‎ OB是北偏西60°，‎ 故选：B．‎ 点评：‎ 本题考查了方向角，方向角的表示方法是北偏东或北偏西，南偏东或南偏西．‎ ‎11. （2014•海南,第8题3分）如图，△ABC与△DEF关于y轴对称，已知A（﹣4，6），B（﹣6，2），E（2，1），则点D的坐标为（　　）‎ ‎　‎ A．‎ ‎（﹣4，6）‎ B．‎ ‎（4，6）‎ C．‎ ‎（﹣2，1）‎ D．‎ ‎（6，2）‎ 考点：‎ 关于x轴、y轴对称的点的坐标．.‎ 分析：‎ 根据关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变．即点P（x，y）关于y轴的对称点P′的坐标是（﹣x，y），进而得出答案．‎ 解答：‎ 解：∵△ABC与△DEF关于y轴对称，A（﹣4，6），‎ ‎∴D（4，6）．‎ 故选：B．‎ 点评：‎ 此题主要考查了关于y轴对称点的性质，准确记忆横纵坐标的关系是解题关键．‎ ‎12．（2014•四川绵阳,第7题3分）线段EF是由线段PQ平移得到的，点P（﹣1，4）的对应点为E（4，7），则点Q（﹣3，1）的对应点F的坐标为（　　）‎ ‎　‎ A．‎ ‎（﹣8，﹣2）‎ B．‎ ‎（﹣2，﹣2）‎ C．‎ ‎（2，4）‎ D．‎ ‎（﹣6，﹣1）‎ 考点：‎ 坐标与图形变化-平移 分析：‎ 首先根据P点的对应点为E可得点的坐标的变化规律，则点Q的坐标的变化规律与P点的坐标的变化规律相同即可．‎ 解答：‎ 解：∵点P（﹣1，4）的对应点为E（4，7），‎ ‎∴P点是横坐标+5，纵坐标+3得到的，‎ ‎∴点Q（﹣3，1）的对应点N坐标为（﹣3+5，1+3），‎ 即（2，4）．‎ 故选：C．‎ 点评：‎ 此题主要考查了坐标与图形变化﹣平移，关键是掌握把一个图形平移后，个点的变化规律都相同．‎ ‎13．(2014•黑龙江牡丹江, 第6题3分)如图，把ABC经过一定的变换得到△A′B′C′，如果△ABC上点P的坐标为（x，y），那么这个点在△A′B′C′中的对应点P′的坐标为（　　）‎ ‎ 第1题图 ‎ A．（﹣x，y﹣2） B． （﹣x，y+2） C． （﹣x+2，﹣y） D． （﹣x+2，y+2）‎ 考点： 坐标与图形变化-旋转；坐标与图形变化-平移．‎ 专题： 几何变换．‎ 分析： 先观察△ABC和△A′B′C′得到把△ABC向上平移2个单位，再关于y轴对称可得到△A′B′C′，然后把点P（x，y）向上平移2个单位，再关于y轴对称得到点的坐标为（﹣x，y+2），即为P′点的坐标．‎ 解答： 解：∵把△ABC向上平移2个单位，再关于y轴对称可得到△A′B′C′，‎ ‎∴点P（x，y）的对应点P′的坐标为（﹣x，y+2）．‎ 故选B．‎ 点评： 本题考查了坐标与图形变化﹣旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．‎ ‎14．（2014•四川遂宁，第6题，4分）点A（1，﹣2）关于x轴对称的点的坐标是（　　）‎ ‎　‎ A．‎ ‎（1，﹣2）‎ B．‎ ‎（﹣1，2）‎ C．‎ ‎（﹣1，﹣2）‎ D．‎ ‎（1，2）‎ 考点：‎ 关于x轴、y轴对称的点的坐标．‎ 分析：‎ 根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数可直接得到答案．‎ 解答：‎ 解：点A（1，﹣2）关于x轴对称的点的坐标是（1，2），‎ 故选；D．‎ 点评：‎ 此题主要考查了关于x轴对称点的坐标特点，关键是掌握点的坐标的变化规律．‎ ‎15．（2014•四川南充，第5题，3分）如图，将正方形OABC放在平面直角坐标系中，O是原点，A的坐标为（1，），则点C的坐标为（　　）‎ ‎　 A．（﹣，1） B． （﹣1，） C． （，1） D． （﹣，﹣1）‎ 分析：过点A作AD⊥x轴于D，过点C作CE⊥x轴于E，根据同角的余角相等求出∠OAD=∠COE，再利用“角角边”证明△AOD和△OCE全等，根据全等三角形对应边相等可得OE=AD，CE=OD，然后根据点C在第二象限写出坐标即可．‎ 解：如图，过点A作AD⊥x轴于D，过点C作CE⊥x轴于E，‎ ‎∵四边形OABC是正方形，∴OA=OC，∠AOC=90°，∴∠COE+∠AOD=90°，‎ 又∵∠OAD+∠AOD=90°，∴∠OAD=∠COE，‎ 在△AOD和△OCE中，，∴△AOD≌△OCE（AAS），‎ ‎∴OE=AD=，CE=OD=1，∵点C在第二象限，∴点C的坐标为（﹣，1）．故选A．‎ 点评： 本题考查了全等三角形的判定与性质，正方形的性质，坐标与图形性质，作辅助线构造出全等三角形是解题的关键，也是本题的难点．‎ ‎16. （2014•山东威海，第7题3分）已知点P（3﹣m，m﹣1）在第二象限，则m的取值范围在数轴上表示正确的是（ ）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 在数轴上表示不等式的解集；解一元一次不等式组；点的坐标．‎ 分析：‎ 根据第二象限内点的坐标特点，可得不等式，根据解不等式，可得答案．‎ 解答：‎ 解：已知点P（3﹣m，m﹣1）在第二象限，‎ ‎3﹣m＜0且m﹣1＞0，‎ 解得m＞3，m＞1，‎ 故选：A．‎ 点评：‎ 本题考查了在数轴上不等式的解集，先求出不等式的解集，再把不等式的解集表示在数轴上．‎ ‎17. （2014•山东威海，第12题3分）如图，在平面直角坐标系xOy中，Rt△OA1C1，Rt△OA2C2，Rt△OA3C3，Rt△OA4C4…的斜边都在坐标轴上，∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°．若点A1的坐标为（3，0），OA1=OC2，OA2=OC3，OA3=OC4…，则依此规律，点A2014的纵坐标为（ ）‎ ‎　‎ A．‎ ‎0‎ B．‎ ‎﹣3×（）2013‎ C．‎ ‎（2）2014‎ D．‎ ‎3×（）2013‎ 考点：‎ 规律型：点的坐标 专题：‎ 规律型．‎ 分析：‎ 根据含30度的直角三角形三边的关系得OA2=OC2=3×；OA3=OC3=3×（）2；OA4=OC4=3×（）3，于是可得到OA2014=3×（）2013，由于而2014=4×503+2，则可判断点A2014在y轴的正半轴上，所以点A2014的纵坐标为3×（）2013．‎ 解答：‎ 解：∵∠A2OC2=30°，OA1=OC2=3，‎ ‎∴OA2=OC2=3×；‎ ‎∵OA2=OC3=3×，‎ ‎∴OA3=OC3=3×（）2；‎ ‎∵OA3=OC4=3×（）2，‎ ‎∴OA4=OC4=3×（）3，‎ ‎∴OA2014=3×（）2013，‎ 而2014=4×503+2，‎ ‎∴点A2014在y轴的正半轴上，‎ ‎∴点A2014的纵坐标为3×（）2013．‎ 故选D．‎ 点评：‎ 本题考查了规律型：点的坐标：通过从一些特殊的点的坐标发现不变的因素或按规律变化的因素，然后推广到一般情况．也考查了含30度的直角三角形三边的关系．‎ ‎18．（2014•湖南张家界，第14题，3分 ‎）若点A（m+2，3）与点B（﹣4，n+5）关于y轴对称，则m+n=　0　．‎ 考点：‎ 关于x轴、y轴对称的点的坐标．‎ 分析：‎ 根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”列出方程求解即可．‎ 解答：‎ 解：∵点A（m+2，3）与点B（﹣4，n+5）关于y轴对称，‎ ‎∴m+2=4，3=n+5，‎ 解得：m=2，n=﹣2，‎ ‎∴m+n=0，‎ 故答案为：0．‎ 点评：‎ 本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：‎ ‎（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；‎ ‎（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；‎ ‎（3）关于原点对称的点，横坐标与纵坐标都互为相反数．‎ 二.填空题 ‎1. （ 2014•广西玉林市、防城港市，第14题3分）在平面直角坐标系中，点（﹣4，4）在第　二　象限．‎ 考点：‎ 点的坐标．‎ 分析：‎ 根据各象限内点的坐标特征解答．‎ 解答：‎ 解：点（﹣4，4）在第二象限．‎ 故答案为：二．‎ 点评：‎ 本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．‎ ‎　‎ ‎2.（2014•邵阳，第16题3分）如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是 （﹣4，3） ．‎ 考点：‎ 坐标与图形变化－旋转 分析：‎ 过点A作AB⊥x轴于B，过点A′作A′B′⊥x轴于B ‎′，根据旋转的性质可得OA=OA′，利用同角的余角相等求出∠OAB=∠A′OB′，然后利用“角角边”证明△AOB和△OA′B′全等，根据全等三角形对应边相等可得OB′=AB，A′B′=OB，然后写出点A′的坐标即可．‎ 解答：‎ 解：如图，过点A作AB⊥x轴于B，过点A′作A′B′⊥x轴于B′，‎ ‎∵OA绕坐标原点O逆时针旋转90°至OA′，‎ ‎∴OA=OA′，∠AOA′=90°，‎ ‎∵∠A′OB′+∠AOB=90°，∠AOB+∠OAB=90°，‎ ‎∴∠OAB=∠A′OB′，‎ 在△AOB和△OA′B′中，‎ ‎，‎ ‎∴△AOB≌△OA′B′（AAS），‎ ‎∴OB′=AB=4，A′B′=OB=3，‎ ‎∴点A′的坐标为（﹣4，3）．‎ 故答案为：（﹣4，3）．‎ 点评：‎ 本题考查了坐标与图形变化﹣旋转，熟记性质并作辅助线构造出全等三角形是解题的关键，也是本题的难点．‎ ‎3.（2014·云南昆明，第12题3分）如图，在平面直角坐标系中，点A坐标为（1，3），将线段OA向左平移2个单位长度，得到线段O′A′，则点A的对应点A′的坐标为 .‎ 考点：‎ 作图－平移变换，平面直角坐标系点的坐标．‎ 分析：‎ 根据网格结构找出OA平移后的对应点O′、A′的位置，然后连接，写出平面直角坐标系中A′的坐标即可．‎ 解答：‎ 解：如图当线段OA向左平移2个单位长度后得到线段O′A′，A′的坐标为 故填 点评：‎ 本题考查了利用平移变换作图，熟练掌握网格结构，准确找出对应点的位置是解题的关键．‎ ‎4. （2014•泰州，第8题，3分）点A（﹣2，3）关于x轴的对称点A′的坐标为　（﹣2，﹣3）　．‎ 考点：‎ 关于x轴、y轴对称的点的坐标 分析：‎ 让点A的横坐标不变，纵坐标互为相反数即可得到点A关于x轴的对称点A′的坐标．‎ 解答：‎ 解：∵点A（﹣2，3）关于x轴的对称点A′，‎ ‎∴点A′的横坐标不变，为﹣2；纵坐标为﹣3，‎ ‎∴点A关于x轴的对称点A′的坐标为（﹣2，﹣3）．‎ 故答案为：（﹣2，﹣3）．‎ 点评：‎ 此题主要考查了关于x轴对称点的性质，用到的知识点为：两点关于x轴对称，横纵坐标不变，纵坐标互为相反数．‎ ‎5. (2014•黑龙江牡丹江, 第20题3分)已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B1在y轴上且坐标是（0，2），点C1、E1、E2、C2、E3、E4、C3在x轴上，C1的坐标是（1，0）．B1C1∥B2C2∥B3C3，以此继续下去，则点A2014到x轴的距离是　　．‎ 第3题图 考点： 全等三角形的判定与性质；规律型：点的坐标；正方形的性质．‎ 分析： 根据勾股定理可得正方形A1B1C1D1的边长为=，根据相似三角形的性质可得后面正方形的边长依次是前面正方形边长的，依次得到第2014个正方形和第2014个正方形的边长，进一步得到点A2014到x轴的距离．‎ 解答： 解：如图，∵点C1、E1、E2、C2、E3、E4、C3在x轴上，B1C1∥B2C2∥B3C3，‎ ‎∴△B1OC1∽△B2E2C2∽B3E4C3…，△B1OC1≌△1CE1D1，…，‎ ‎∴B2E2=1，B3E4=，B4E6=，B5E8=…，‎ ‎∴B2014E4016=，‎ 作A1E⊥x轴，延长A1D1交x轴于F，‎ 则△C1D1F∽△C1D1E1，‎ ‎∴=，‎ 在Rt△OB1C1中，OB1=2，OC1=1，‎ 正方形A1B1C1D1的边长为为=，‎ ‎∴D1F=，‎ ‎∴A1F=，‎ ‎∵A1E∥D1E1，‎ ‎∴=，‎ ‎∴A1E=3，∴=，‎ ‎∴点A2014到x轴的距离是×=‎ 点评： 此题主要考查了正方形的性质以及解直角三角形的知识，得出正方形各边长是解题关键．‎ ‎6. （2014•湖北荆门,第14题3分）如图，正方形OABC与正方形ODEF是位似图形，点O为位似中心，相似比为1：，点A的坐标为（0，1），则点E的坐标是　（，）　．‎ 第4题图 考点： 位似变换；坐标与图形性质．‎ 分析： 由题意可得OA：OD=1：，又由点A的坐标为（1，0），即可求得OD的长，又由正方形的性质，即可求得E点的坐标．‎ 解答： 解：∵正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为1：，‎ ‎∴OA：OD=1：，‎ ‎∵点A的坐标为（1，0），‎ 即OA=1，‎ ‎∴OD=，‎ ‎∵四边形ODEF是正方形，‎ ‎∴DE=OD=．‎ ‎∴E点的坐标为：（，）．‎ 故答案为：（，）．‎ 点评： 此题考查了位似变换的性质与正方形的性质．此题比较简单，注意理解位似变换与相似比的定义是解此题的关键．‎ ‎7．（2014•青岛，第11题3分）如图，△ABC的顶点都在方格线的交点（格点）上，如果将△ABC绕C点按逆时针方向旋转90°，那么点B的对应点B′的坐标是　（1，0）　．‎ 考点：‎ 坐标与图形变化-旋转．.‎ 专题：‎ 数形结合．‎ 分析：‎ 先画出旋转后的图形，然后写出B′点的坐标．‎ 解答：‎ 解：如图，将△ABC绕C点按逆时针方向旋转90°，点B的对应点B′的坐标为（1，0）．‎ 故答案为（1，0）．‎ 点评：‎ 本题考查了坐标与图形变化﹣旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．‎ ‎8. （2014•湖南衡阳,第20题3分）如图，在平面直角坐标系xOy中，已知点M0的坐标为（1，0），将线段OM0绕原点O逆时针方向旋转45°，再将其延长到M1，使得M1M0⊥OM0，得到线段OM1；又将线段OM1绕原点O逆时针方向旋转45°，再将其延长到M2，使得M2M1⊥OM1，得到线段OM2；如此下去，得到线段OM3，OM4，OM5，…‎ 根据以上规律，请直接写出OM2014的长度为　21007　．‎ 考点： 规律型：点的坐标．.‎ 专题： 规律型．‎ 分析： 根据点M0的坐标求出OM0，然后判断出△OM0M1是等腰直角三角形，然后根据等腰直角三角形的性质求出OM1，同理求出OM2，OM3，然后根据规律写出OM2014即可．‎ 解答： 解：∵点M0的坐标为（1，0），‎ ‎∴OM0=1，‎ ‎∵线段OM0绕原点O逆时针方向旋转45°，M1M0⊥OM0，‎ ‎∴△OM0M1是等腰直角三角形，‎ ‎∴OM1=OM0=，‎ 同理，OM2=OM1=（）2，‎ OM3=OM2=（）3，‎ ‎…，‎ OM2014=OM2013=（）2014=21007．‎ 故答案为：21007．‎ 点评： 本题是对点的坐标变化规律的考查，主要利用了等腰直角三角形的判定与性质，读懂题目信息，判断出等腰直角三角形是解题的关键．‎ ‎9. （2014•贵州黔西南州, 第14题3分）点P（2，3）关于x轴的对称点的坐标为　（2，﹣3）　．‎ 考点：‎ 关于x轴、y轴对称的点的坐标．‎ 分析：‎ 根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数．即点P（x，y）关于x轴的对称点P′的坐标是（x，﹣y）得出即可．‎ 解答：‎ 解：∵点P（2，3）‎ ‎∴关于x轴的对称点的坐标为：（2，﹣3）．‎ 故答案为：（2，﹣3）．‎ 点评：‎ 此题主要考查了关于x轴、y轴对称点的性质，正确记忆坐标规律是解题关键．‎ ‎　‎ ‎10． （2014•贵州黔西南州, 第20题3分）在平面直角坐标系中，对于平面内任一点（m，n），规定以下两种变换：‎ ‎（1）f（m，n）=（m，﹣n），如f（2，1）=（2，﹣1）；‎ ‎（2）g（m，n）=（﹣m，﹣n），如g （2，1）=（﹣2，﹣1）‎ 按照以上变换有：f[g（3，4）]=f（﹣3，﹣4）=（﹣3，4），那么g[f（﹣3，2）]=　（3，2）　．‎ 考点：‎ 点的坐标．‎ 专题：‎ 新定义．‎ 分析：‎ 由题意应先进行f方式的运算，再进行g方式的运算，注意运算顺序及坐标的符号变化．‎ 解答：‎ 解：∵f（﹣3，2）=（﹣3，﹣2），‎ ‎∴g[f（﹣3，2）]=g（﹣3，﹣2）=（3，2），‎ 故答案为（3，2）．‎ 点评：‎ 本题考查了一种新型的运算法则，考查了学生的阅读理解能力，此类题的难点是判断先进行哪个运算，关键是明白两种运算改变了哪个坐标的符号．‎ ‎11．（2014•四川宜宾，第13题，3分）在平面直角坐标系中，将点A（﹣1，2）向右平移3个单位长度得到点B，则点B关于x轴的对称点C的坐标是 （2，﹣2） ． ‎ 考点：‎ 坐标与图形变化－平移；关于x轴、y轴对称的点的坐标 分析：‎ 首先根据横坐标，右移加，左移减可得B点坐标，然后再关于x轴对称点的坐标特点可得答案．‎ 解答：‎ 解：点A（﹣1，2）向右平移3个单位长度得到的B的坐标为（﹣1+3，2），即（2，2），‎ 则点B关于x轴的对称点C的坐标是（2，﹣2），‎ 故答案为：（2，﹣2）．‎ 点评：‎ 此题主要考查了坐标与图形变化﹣平移，以及关于x轴对称点的坐标，关键是掌握点的坐标变化规律．‎ ‎12. （2014•黑龙江绥化,第10题3分）如图，在平面直角坐标系中，已知点A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），把一根长为2014个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在A处，并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上，则细线的另一端所在位置的点的坐标是　（﹣1，﹣1）　．‎ 考点：‎ 规律型：点的坐标．‎ 分析：‎ 根据点的坐标求出四边形ABCD的周长，然后求出另一端是绕第几圈后的第几个单位长度，从而确定答案．‎ 解答：‎ 解：∵A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），‎ ‎∴AB=1﹣（﹣1）=2，BC=1﹣（﹣2）=3，CD=1﹣（﹣1）=2，DA=1﹣（﹣2）=3，‎ ‎∴绕四边形ABCD一周的细线长度为2+3+2+3=10，‎ ‎2014÷10=201…4，‎ ‎∴细线另一端在绕四边形第202圈的第4个单位长度的位置，‎ 即线段BC的中间位置，点的坐标为（﹣1，﹣1）．‎ 故答案为：（﹣1，﹣1）．‎ 点评：‎ 本题主要考查了点的变化规律，根据点的坐标求出四边形ABCD一周的长度，从而确定2014个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键．‎ 三.解答题 ‎1. （2014•湘潭，第17题）在边长为1的小正方形网格中，△AOB的顶点均在格点上，‎ ‎（1）B点关于y轴的对称点坐标为　（﹣3，2）　；‎ ‎（2）将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；‎ ‎（3）在（2）的条件下，A1的坐标为　（﹣2，3）　．‎ ‎（第1题图）‎ 考点：‎ 作图－平移变换；关于x轴、y轴对称的点的坐标．‎ 分析：‎ ‎（1）根据关于y轴对称的点的横坐标互为相反数，纵坐标相等解答；‎ ‎（2）根据网格结构找出点A、O、B向左平移后的对应点A1、O1、B1的位置，然后顺次连接即可；‎ ‎（3）根据平面直角坐标系写出坐标即可．‎ 解答：‎ 解：（1）B点关于y轴的对称点坐标为（﹣3，2）；‎ ‎（2）△A1O1B1如图所示；‎ ‎（3）A1的坐标为（﹣2，3）．‎ 故答案为：（1）（﹣3，2）；（3）（﹣2，3）．‎ 点评：‎ 本题考查了利用平移变换作图，关于y轴对称点的坐标，熟练掌握网格结构准确找出对应点的位置是解题的关键．‎ ‎2．（2014·浙江金华，第19题6分）在棋盘中建立如图所示的直角坐标系，三颗棋子A，O，B的位置如图，它们的坐标分别是，（0，0），（1，0）.‎ ‎（1）如图2，添加棋C子，使四颗棋子A，O，B，C成为一个轴对称图形，请在图中画出该图形的对称轴；‎ ‎（2）在其他格点位置添加一颗棋子P，使四颗棋子A，O，B，P成为轴对称图形，请直接写出棋子P的位置的坐标. （写出2个即可）‎ ‎3. （2014•四川巴中，第24题7分）如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A（﹣2，4），B（﹣2，1），C（﹣5，2）．‎ ‎（1）请画出△ABC关于x轴对称的△A1B1C1．‎ ‎（2）将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以﹣2，得到对应的点A2，B2，C2，请画出△A2B2C2．‎ ‎（3）求△A1B1C1与△A2B2C2的面积比，即：=　1：4　（不写解答过程，直接写出结果）．‎ 考点：平面直角坐标系，相似三角形的面积比．‎ 分析： （1）根据关于x轴对称点的性质得出对应点位置进而得出答案；‎ ‎（2）根据将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以﹣2，得出各点坐标，进而得出答案；‎ ‎（3）利用位似图形的性质得出位似比，进而得出答案．‎ 解答：（1）如图所示：△A1B1C1即为所求；‎ ‎（2）如图所示：△A2B2C2即为所求；‎ ‎（3）∵将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以﹣2，得到对应的点A2，B2，C2，‎ ‎∴△A1B1C1与△A2B2C2的相似比为：1：2，‎ ‎∴：=1：4．故答案为：1：4．‎ 点评： 此题主要考查了位似变换以及轴对对称变换，得出对应点位置是解题关键．‎