中考数学综合题专题复习圆专题解析 27页

中考数学综合题专题复习【圆】专题解析 ‎ ‎ 一. 教学内容：‎ ‎ 1. 圆的内容包括：圆的有关概念和基本性质，直线和圆的位置关系，圆和圆的位置关系，正多边形和圆。‎ ‎ 2. 主要定理：‎ ‎ （1）垂径定理及其推论。‎ ‎ （2）圆心角、弧、弦、弦心距之间的关系定理。‎ ‎ （3）圆周角定理、弦切角定理及其推论。‎ ‎ （4）圆内接四边形的性质定理及其推论。‎ ‎ （5）切线的性质及判定。‎ ‎ （6）切线长定理。‎ ‎ （7）相交弦、切割线、割线定理。‎ ‎ （8）两圆连心线的性质，两圆的公切线性质。‎ ‎ （9）圆周长、弧长；圆、扇形，弓形面积。‎ ‎ （10）圆柱、圆锥侧面展开图及面积计算。‎ ‎ （11）正n边形的有关计算。‎ ‎ ‎ 二. 中考聚焦：‎ ‎ 圆这一章知识在中考试题中所占的分数比例大约如下表：‎ ‎ 圆的知识在中考中所占的比例大，题型多，常见的有填空题、选择题、计算题或证明题，近年还出现了一些圆的应用题及开放型问题、设计型问题，中考的压轴题都综合了圆的知识。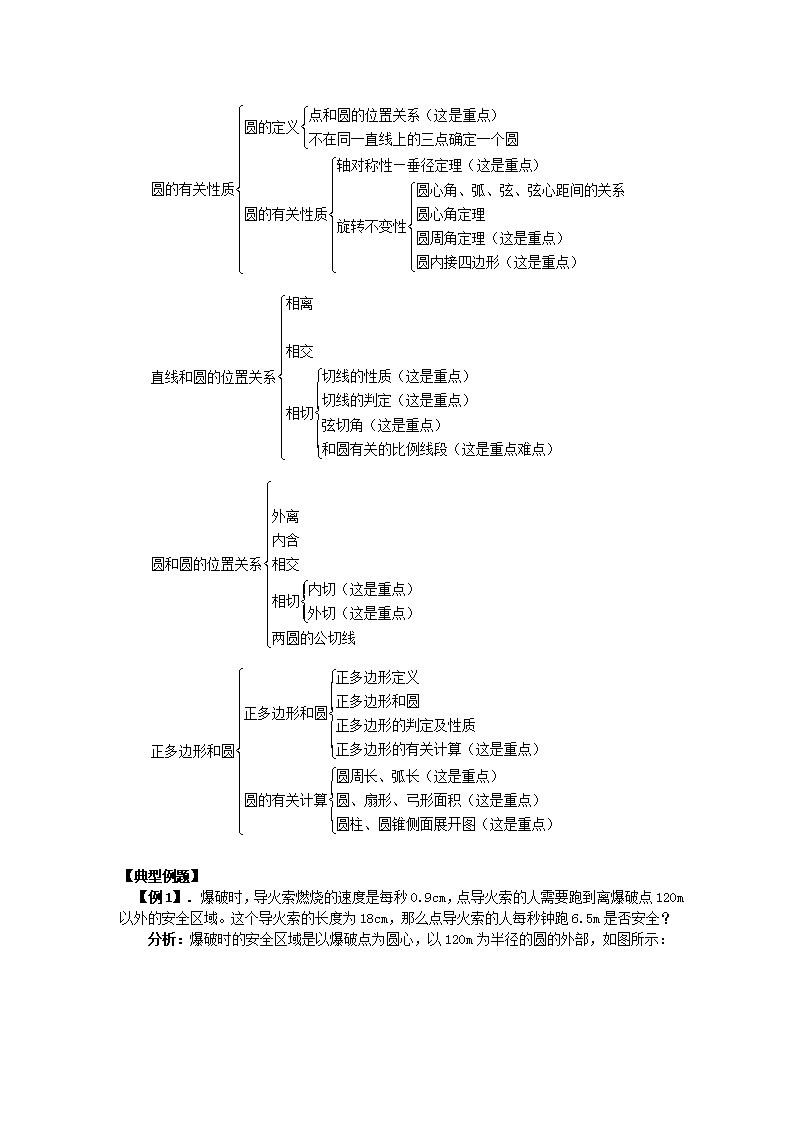‎ 三. 知识框图：‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎【典型例题】‎ ‎ 【例1】. 爆破时，导火索燃烧的速度是每秒‎0.9cm，点导火索的人需要跑到离爆破点‎120m以外的安全区域。这个导火索的长度为‎18cm，那么点导火索的人每秒钟跑‎6.5m是否安全？‎ ‎ 分析：爆破时的安全区域是以爆破点为圆心，以‎120m为半径的圆的外部，如图所示：‎ ‎ 解：‎ ‎ ‎ ‎ ‎ ‎ ∴点导火索的人非常安全 ‎ 【例2】. 已知梯形ABCD内接于⊙O，AB∥CD，⊙O的半径为4，AB＝6，CD＝2，求梯形ABCD的面积。‎ ‎ 分析：要求梯形面积必须先求梯形的高，即弦AB、CD间距离，为此要构造直角三角形利用勾股定理求高。为了便于运用垂径定理，故作OE⊥CD于E，延长EO交AB于F，证OF⊥AB。‎ ‎ 此题容易出现丢解的情况，要注意分情况讨论。‎ ‎ 解：分两种情况讨论：‎ ‎ （1）当弦AB、CD分别在圆心O的两侧时，如图（1）：‎ ‎ 过O作OE⊥CD于E，延长EO交AB于F ‎ 连OC、OB，则CE＝DE ‎ ∵AB∥CD，OE⊥CD ‎ ∴OF⊥AB，即EF为梯形ABCD的高 ‎ 在Rt△OEC中，∵EC＝1，OC＝4‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ （2）当弦AB、CD在圆心O的同侧时，如图（2）：‎ ‎ 过O作OE⊥CD于E，交AB于F ‎ 以下证法同（1），略。‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 【例3】. 如图，已知AB为⊙O的直径，P是OB的中点，求tanC·tanD的值。‎ ‎ 分析：为了求tanC·tanD的值，需要分别构造出含有∠C和∠D的两个直角三角形。而AB是直径，为我们寻找直角创造了条件。连BC、BD，则得到Rt△ACB和Rt△ADB。可以发现∠ACD＝∠ABD，∠ADC＝∠ABC，于是，可以把tanC·tanD转化为 ‎ 解：连结BC、BD ‎ ∵AB是⊙O的直径，∴∠ACB＝∠ADB＝90°‎ ‎ ∵∠ACD＝∠ABD，∠ADC＝∠ABC ‎ ‎ ‎ 作AE⊥CD于E，作BF⊥CD于F ‎ 则△AEC∽△ADB ‎ ‎ ‎ ∴AC·AD＝AE·AB ‎ 同理，BD·BC＝BF·AB ‎ ‎ ‎ ∵△APE∽△BPF ‎ ‎ ‎ ∵P为半径OB的中点 ‎ ‎ ‎ ∴tanC·tanD＝3‎ ‎ 【例4】. ‎ ‎ 分析：由已知条件，等边△ABC可得60°角，根据圆的性质，可得∠ADB＝60°，利用截长补短的方法可得一个新的等边三角形，再证两个三角形全等，从而转移线段DC。‎ ‎ 证明：延长DB至点E，使BE＝DC，连结AE ‎ ∵△ABC是等边三角形 ‎ ∴∠ACB＝∠ABC＝60°，AB＝AC ‎ ∴∠ADB＝∠ACB＝60°‎ ‎ ∵四边形ABDC是圆内接四边形 ‎ ∴∠ABE＝∠ACD ‎ 在△AEB和△ADC中，‎ ‎ ‎ ‎ ‎ ‎ ∴AE＝AD ‎ ∵∠ADB＝60°‎ ‎ ∴△AED是等边三角形 ‎ ∴AD＝DE＝DB＋BE ‎ ∵BE＝DC ‎ ∴DB＋DC＝DA ‎ 说明：本例也可以用其他方法证明。如：‎ ‎ （1）延长DC至F，使CF＝BD，连结AF，再证△ACF≌△ABD，得出AD＝DF，从而DB＋CD＝DA。‎ ‎ （2）在DA上截取DG＝DC，连结CG，再证△BDC≌△AGC，得出BD＝AG，从而DB＋CD＝DA。‎ ‎ 【例5】. 如图，已知四边形ABCD内接于⊙O，AB是直径，AD＝DC，分别延长BA、CD交于点E，BF⊥EC交EC的延长线于F，若EA＝AO，BC＝12，求CF的长。‎ ‎ 分析：在Rt△CFB中，已知BC＝12，求CF，故可寻找与之相似的直角三角形，列比例式求解。‎ ‎ 解：连结OD，BD ‎ ‎ ‎ ∴∠ABC＝∠AOD ‎ ∴OD∥BC ‎ ‎ ‎ ∵EA＝AO，∴EA＝AO＝BO ‎ ‎ ‎ ∴AB＝16，BE＝24‎ ‎ ∵四边形ABCD内接于⊙O ‎ ∴∠EDA＝∠EBC ‎ ∵∠E是公共角 ‎ ∴△EDA∽△EBC ‎ ‎ ‎ 设AD＝DC＝x，ED＝y，则有 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ∵AB为⊙O的直径 ‎ ∴∠ADB＝∠F＝90°‎ ‎ 又∠DAB＝∠FCB ‎ ∴Rt△ADB∽Rt△CFB ‎ ‎ ‎ ‎ ‎ 说明：与圆有关的问题，大都与相似三角形联系在一起。‎ ‎ 此题运用了两次相似三角形，找到线段之间的关系，并且运用了方程的思想解几何问题，这是解几何问题的一种重要方法。‎ ‎ 【例6】. 如图，已知等腰△ABC中，AB＝AC，以AB为直径的⊙O分别交AC、BC于 ‎ 解：连结FD ‎ ∵AB是直径，∴AD⊥BC ‎ ∵AB＝AC，∴BD＝DC，∠FAD＝∠DAB ‎ ∵四边形ABDF是圆内接四边形 ‎ ∴∠CFD＝∠B ‎ ∵∠C是公共角 ‎ ∴△ABC∽△DFC ‎ ‎ ‎ ∵AB＝AC ‎ ∴CD＝DF ‎ （也可以证∠CFD＝∠B，∵AB＝AC，∴∠B＝∠C，∴∠C＝∠CFD，∴CD＝DF。）‎ ‎ ∵DE切⊙O于D ‎ ∴∠FAD＝∠EDF ‎ 又∵∠CDE＋∠EDF＝∠FAD＋∠DAB ‎ ∴∠CDE＝∠DAB ‎ ∴∠CDE＝∠EDF ‎ ∵CD＝FD ‎ ∴CE＝EF，DE⊥CF ‎ ‎ ‎ ‎ ‎ ‎ ‎ ∴设CD＝3x，AC＝5x ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ∴EC＝9‎ ‎ 【例7】. 如图，相交两圆的公共弦长为‎120cm，它分别是一圆内接正六边形的边和另一圆内接正方形的边。求两圆相交弧间阴影部分的面积。‎ ‎ 解：∵公共弦AB＝120‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 【例8】.一个长方体的香烟盒里，装满大小均匀的20支香烟。打开烟盒的顶盖后，二十支香烟排列成三行，如图（1）所示。经测量，一支香烟的直径约为‎0.75cm，长约为‎8.4cm。‎ ‎ （1）试计算烟盒顶盖ABCD的面积（本小题计算结果不取近似值）。‎ ‎ （2）制作这样一个烟盒至少需要多少面积的纸张（不计重叠粘合的部分，计算结果 ‎ 解题点拨：四边形ABCD中，AD长为7支香烟的直径之和，易求；求AB长，只要计算出如图（2）中的O1E长即可。‎ ‎ 解：（1）如图（2），作O1E⊥O2O3‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ∴四边形ABCD的面积是：‎ ‎ ‎ ‎ （2）制作一个烟盒至少需要纸张：‎ ‎ ‎ ‎ 【例9】. 在直径为‎20cm的圆中，有一弦长为‎16cm，求它所对的弓形的高。‎ ‎ 解：一小于直径的弦所对的弓形有两个：劣弧弓形与优弧弓形。‎ ‎ 如图，HG为⊙O的直径，且HG⊥AB，AB＝‎16cm，HG＝‎‎20cm ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 故所求弓形的高为‎4cm或‎16cm ‎【例10】.‎ 求：∠CAD所夹圆内部分的面积。‎ ‎ 解：符合题设条件的图形有两种情况：‎ ‎ （1）圆心O在∠CAD的内部，如图（1），连结OC、OD，过O作OE⊥AD于点E ‎ ‎ ‎ ∴OC⊥AB ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ （2）圆心O在∠DAC的外部时，如图（2），有：‎ ‎ ‎ ‎ ‎ ‎【例11】. ‎ ‎ 分析：由已知条件可知AB、CD弦的位置不确定，所以要分多种情况讨论，可分为四种情况。‎ ‎ 解：（1）当AB、CD不相交时，且AB、CD在圆心的两侧，如图（1）连结OD、OB。‎ ‎ ∵M、N分别是弦AB、CD的中点，OD、OB过圆心O ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 图（1）‎ ‎ （2）当AB、CD不相交，且在圆心O的同侧时，如图（2），连结OB、OC ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 图（2）‎ ‎ （3）当AB、CD相交于点P，且圆心O在∠DPA的内部时，如图（3），∠DPA是圆内角，‎ ‎ ‎ ‎ ‎ 图（3）‎ ‎ （4）当AB、CD相交于点P，且圆心O在∠DPA的外部时，如图（4）‎ ‎ ‎ ‎ ‎ ‎ ‎ 图（4）‎ ‎ 【例12】.已知：如图，圆心A（0，-3），圆A与x轴相切，圆B的圆心B在x正半轴上，且圆B与圆A外切于点P。两圆内公切线MP交y轴于点M，交x轴于点N：（1）求证△AOB∽△NPB；（2）设圆A半径为r1，圆B半径为r2，若r1：r2＝3：2，求点M、N的坐标及公切线MP的函数解析式；（3）设点B（x1，0），点B关于y轴的对称点B’（x2，0），若x1·x2＝-6，求过B’、A、B三点的抛物线解析式；（4）若圆A的位置大小不变，圆心B在x正半轴上移动，并始终有圆B与圆A外切，过点M作圆B的切线MC，C为切点，MC＝时，B点在x轴的什么位置？从你的解答中能获得什么猜想？‎ ‎ 解：（1）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 设直线MP的解析式为y＝kx＋b，‎ ‎ ‎ ‎ ‎ ‎ （3）设抛物线为y＝ax2＋bx＋c（a≠0）‎ ‎ 令y＝0，则有ax2＋bx＋c＝0‎ ‎ ∵B与B’关于y轴对称，‎ ‎ ∴x1＋x2＝0，即b＝0，‎ ‎ 又点A（0，-3），∴C=-3‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ （4）∵MC＝MP ‎ ∴可证△APM≌△AOB ‎ ‎ ‎ ‎ ‎ 猜想：圆心B在x轴的正半轴上任一位置时，都有切线MP的长等于点B的横坐标或四边形MOBC是长方形。‎ ‎【模拟试题】‎ 一. 选择题：（本题共24分，每小题4分，每道题只有一个正确答案）‎ ‎ 1. 已知AB是⊙O的直径，半径EO⊥AB于O，弦CD⊥EO于F点，若∠CDB＝120°，则的度数为（ ）‎ ‎ A. 10° B. 15° C. 30° D. 60°‎ ‎ 2. 如图，已知⊙O中，M是弦CD的中点，N为弦AB的中点，并且的度数为130°、90°，则∠MON的度数为（ ）‎ ‎ A. 70° B. 90° C. 130° D. 160°‎ ‎ 3. 已知△ABC中，a、b、c是∠A、∠B、∠C的对边，若r是内切圆半径，则△ABC的面积可以表示为（ ）‎ ‎ A. B. ‎ ‎ C. D. ‎ ‎ 4. 已知两圆的半径分别为R、r，且圆心距为d，若，则这两圆的位置关系为（ ）‎ ‎ A. 外离或外切 B. 相交或内切 ‎ C. 外切或内切 D. 内切或内含 ‎ 5. 已知正多边形的边长为a与外接圆半径R之间满足，则这个多边形是（ ）‎ ‎ A. 正三边形 B. 正四边形 C. 正五边形 D. 正六边形 ‎ 6. 已知正方形ABCD边长为5，剪去四个角后成正八边形，则正八边形的边长为（ ）‎ ‎ A. B. C. D. ‎ 二. 填空题：（本题共16分，每小题4分）‎ ‎ 7. 已知△ABC，∠C＝90°，∠B＝28°，以C为圆心，以CA为半径的圆交AB于D，则的度数为_____________。‎ ‎ 8. 已知△ABC内接于⊙O，F、E是的三分之一点，若∠AFE＝130°，则∠C＝____________度。‎ ‎ 9. 已知PA切⊙O于A，∠APO＝30°，若，OP交于⊙O于C，则PC＝____________。‎ ‎ 10. 两圆半径之比为2：1，大圆内接正六边形与小圆外切正六边形的面积比为_______。‎ 三. 求解下列各题：（本题共18分，每小题6分）‎ ‎ 11. 已知AB是⊙O的直径，弦CD⊥AB于E，若弦CD把⊙O分为2：1的两部分，且，求⊙O的直径及AE长。‎ ‎ 12. 已知等边△ABC内接于⊙O，E是上一点，AE交BC于D，若BD：DC＝2：1，且AB＝6，求DE长。‎ ‎ 13. 如图所示，AB是⊙O的弦，EF切⊙O于B，AC⊥EF于C。‎ ‎ 求证：‎ 四. 解答题：（本题共24分，每小题8分）‎ ‎ 14. 如图所示，AB切⊙O于B，AE过O点交⊙O于E、C，过C作⊙O切线交AB于D，若。‎ ‎ 求证：‎ ‎ 15. 如图所示，△ABC中，∠A＝90°，O是BC上一点，以O为圆心的圆切AB、AC于D、E，若AB＝3，AC＝4，求阴影部分的面积。‎ ‎ 16. 如图所示，⊙O与⊙O'交于A、B，过A点任意作两圆的割线CAD，若连结CB、DB，问因割线CAD的位置不确定，∠CBD的大小是否改变？‎ 五. 解答题：（本题共18分，每小题9分）‎ ‎ 17. 如图所示，PA切⊙O于A，PO交⊙O于B、C，若，AE交BC于D，且∠BEA＝30°，DB＝1，求AP及PB长。‎ ‎ 18. 已知一块直径为‎30cm的圆形铁板，已经截去直径分别为‎20cm，‎10cm的圆形铁板各一块。现在剩余的铁板中再截出两块同样大小的圆形，问这两个圆形的最大半径是多少？‎ ‎[参考答案]‎ 一. 选择题。‎ ‎ 1. D ‎ 2. D ‎ 3. B ‎ 提示：设△ABC的内切圆的圆心为O ‎ 连结OA、OB、OC，则△ABC可分割成三个三角形：△ABO，△BCO，△ACO ‎ 则 ‎ ‎ ‎ 应选B ‎ 4. C ‎ 提示：依题意，有：‎ ‎ ‎ ‎ ‎ ‎ 所以，或 ‎ 即，或 ‎ 两圆内切或外切 ‎ 5. C ‎ 提示：正多边形的边数越多，则边长越小，而有 ‎ 因为，，所以 ‎ 则，是正五边形，应选C。‎ ‎ 6. D ‎ 提示：如图所示，所截的四个角是全等的等腰三角形，且GE＝EF＝FH ‎ 设EF＝x，则根据勾股定理，‎ ‎ 则有 ‎ 即 ‎ ‎ ‎ 应选D 二. 填空题。‎ ‎ 7. 56°‎ ‎ 8. 75°或105°‎ ‎ 提示：如图所示：‎ ‎ ∵∠AFE＝130°，∴的度数为260°‎ ‎ 则的度数为 ‎ ∵F、E是的三分之一点 ‎ ‎ ‎ 或 ‎ 9. 12‎ ‎ 10. 3：1‎ ‎ 如图所示，设大圆与小圆的半径为2r和r ‎ 则大圆内接正六边形的边长为2r，小圆外切正六边形的边长为 ‎ 因为这两个正六边形相似，所以面积比等于边长比的平方 ‎ 即 三. 求解下列各题：‎ ‎ 11. 解：如图，分两种情况：（1）点E在OA上；（2）点E在OB上 ‎ （1）∵直径AB⊥弦CD于E，‎ ‎ ∴根据垂径定理，有：‎ ‎ A、B分别为和的中点 ‎ ∵CD把⊙O分成2：1两部分 ‎ ∴的度数为120°，的度数为240°‎ ‎ 连结BC，则 ‎ 在中，‎ ‎ ‎ ‎ （2）当点E在OB上时，AE＝6‎ ‎ ∴直径为8，AE＝6或2‎ ‎ 12. 解法一：如图（1），∵△ABC是等边三角形，AB＝6‎ 图（1）‎ ‎ ∴BC＝AB＝AC＝6，∠B＝∠ACB＝60°‎ ‎ ∵BD：DC＝2：1‎ ‎ ∴BD＝4，CD＝2‎ ‎ ∴AD·DE＝BD·CD＝8‎ ‎ 连结CE，∵∠B＝∠E＝60°‎ ‎ ∴∠ACB＝∠E ‎ ∵∠CAD是公共角 ‎ ∴△ACD∽△AEC ‎ ‎ ‎ ‎ ‎ 解法二：如图（2），过A作AG⊥BC于G 图（2）‎ ‎ ∵△ABC是等边三角形，BC＝6‎ ‎ ∴CG＝GB＝3‎ ‎ 由解法一得：CD＝2，BD＝4‎ ‎ ∴DG＝1‎ ‎ 在中，‎ ‎ 在中，‎ ‎ 根据相交弦定理，有：‎ ‎ ‎ ‎ ‎ ‎ 13. 证明一：延长AD交⊙O于D，连结BD，如图（1）‎ ‎ ∵AD是直径，∴∠ABD＝90°，2AO＝AD ‎ ∵EF切⊙O于B ‎ ∴∠1＝∠D ‎ ∵AC⊥EF于C ‎ ∴∠C＝∠ABD＝90°‎ ‎ ∴△ABC∽△ADB ‎ ‎ ‎ 即 ‎ 证明二：延长AC至M，使CM＝AC，连结BM、OB 图（2）‎ ‎ ∵BC⊥AC，AC＝CM ‎ ∴MB＝AB ‎ ∴∠M＝∠2‎ ‎ ∵OA＝OB ‎ ∴∠3＝∠4‎ ‎ ∵EF切⊙O于B ‎ ∴OB⊥EF ‎ ∴AC∥OB ‎ ∴∠2＝∠3‎ ‎ ∴∠2＝∠3＝∠4＝∠M ‎ ‎ 四. 解答题。‎ ‎ 14. 证明：如图，依题意，设BD＝x，则AD＝2x ‎ ∵AB、CD切⊙O于B、C点 ‎ ∴BD＝CD＝x，OC⊥CD ‎ ∴∠ACD＝90°‎ ‎ ‎ ‎ ∵AB是切线，ACE是割线 ‎ ‎ ‎ 即 ‎ ‎ ‎ 15. 解：如图，连结OD，OE ‎ ∵AB、AC切⊙O于D、E ‎ ∴OD⊥AB，OE⊥AC，AD＝AE ‎ ∵∠A＝90°‎ ‎ ∴四边形ADOE是正方形 ‎ ∴∠DOE＝90°‎ ‎ 设AD＝OE＝x ‎ ∵DE∥AD，AB＝3，AC＝4‎ ‎ ‎ ‎ 解得：‎ ‎ ‎ ‎ ‎ ‎ 16. 解：大小不改变 ‎ ∵∠C所对的弧为 ‎ ∠D所对的弧为 ‎ ∴∠C、∠D的度数不变 ‎ 在△BCD中，不变 五. 解答题。‎ ‎ 17. 解：如图，连结AB ‎ ∵，BC是直径 ‎ ∴根据垂径定理的推论，可知：‎ ‎ AD⊥BC，AD＝DE，‎ ‎ ∵∠BEA＝30°‎ ‎ ∴∠DAB＝∠E＝∠BAP＝30°‎ ‎ 在 ‎ ‎ ‎ ∵AD⊥BC，BC为直径 ‎ ，即 ‎ ‎ ‎ 18. 解：如图（1）：‎ 图（1）‎ ‎ 依题意有：‎ ‎ ⊙O1的直径为‎10cm，则半径为‎5cm ‎ ⊙O2的直径为‎20cm，则半径为‎10cm ‎ ⊙O的直径为‎30cm，则半径为‎15cm ‎ 设⊙O与⊙O1，⊙O2，⊙O3相切，半径为r ‎ 延长OO3交⊙O于B，则：‎ ‎ ‎ ‎ 则此题转化为解三角形问题，如图（2）：‎ 图（2）‎ ‎ 设，则 ‎ ‎ ‎ 在和中，有：‎ ‎ ‎ ‎ 在和中，有：‎ ‎ ‎ ‎ ‎ ‎ 整理得：‎ ‎ ‎ ‎ 得：‎ ‎ ‎ ‎ 答：这两个圆形的最大半径是。‎