中考数学圆压轴题 8页

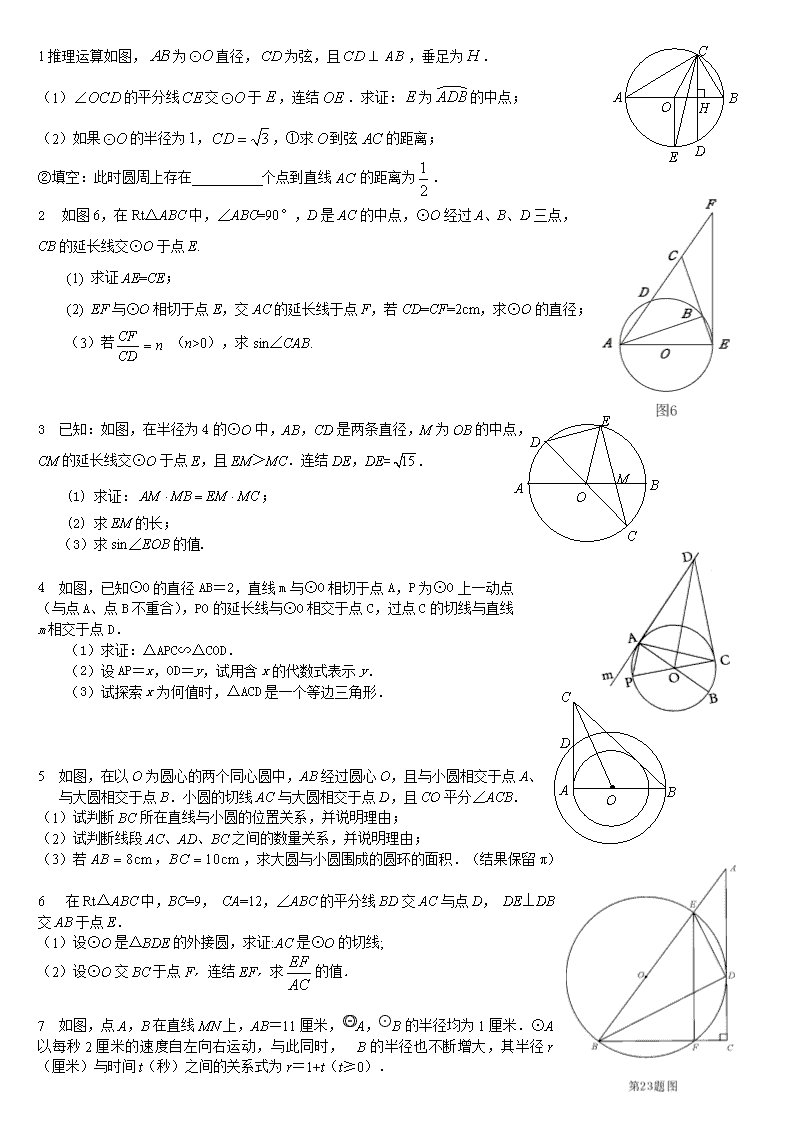
A B D E O C H ‎1推理运算如图，为直径，为弦，且，垂足为．‎ ‎（1）的平分线交于，连结．求证：为的中点；‎ ‎（2）如果的半径为，，①求到弦的距离；‎ ‎②填空：此时圆周上存在 个点到直线的距离为．‎ 2 如图6，在Rt△ABC中，∠ABC=90°，D是AC的中点，⊙O经过A、B、D三点，‎ CB的延长线交⊙O于点E.‎ (1) 求证AE=CE； ‎ (2) EF与⊙O相切于点E，交AC的延长线于点F，若CD=CF=‎2cm，求⊙O的直径；‎ ‎ （3）若 （n>0），求sin∠CAB. ‎ A B C E D O M ‎3 已知：如图，在半径为4的⊙O中，AB，CD是两条直径，M为OB的中点，‎ CM的延长线交⊙O于点E，且EM＞MC．连结DE，DE=.‎ ‎(1) 求证：；‎ ‎(2) 求EM的长；‎ ‎（3）求sin∠EOB的值.‎ ‎4 如图，已知⊙O的直径AB＝2，直线m与⊙O相切于点A，P为⊙O上一动点 ‎（与点A、点B不重合），PO的延长线与⊙O相交于点C，过点C的切线与直线 m相交于点D．‎ ‎（1）求证：△APC∽△COD．‎ ‎（2）设AP＝x，OD＝y，试用含x的代数式表示y．‎ C B O A D ‎（3）试探索x为何值时，△ACD是一个等边三角形．‎ ‎5 如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A、‎ 与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．‎ ‎（1）试判断BC所在直线与小圆的位置关系，并说明理由；‎ ‎（2）试判断线段AC、AD、BC之间的数量关系，并说明理由；‎ ‎（3）若，求大圆与小圆围成的圆环的面积．（结果保留π）‎ ‎6 在Rt△ABC中，BC=9， CA=12，∠ABC的平分线BD交AC与点D， DE⊥DB交AB于点E．‎ ‎（1）设⊙O是△BDE的外接圆，求证:AC是⊙O的切线;‎ ‎（2）设⊙O交BC于点F，连结EF，求的值．‎ ‎7 如图，点A，B在直线MN上，AB＝‎11厘米，⊙A，⊙B的半径均为‎1厘米．⊙A以每秒‎2厘米的速度自左向右运动，与此同时，⊙B的半径也不断增大，其半径r（厘米）与时间t（秒）之间的关系式为r＝1+t（t≥0）． ‎ ‎（1）试写出点A，B之间的距离d（厘米） ‎ A B N M 与时间t（秒）之间的函数表达式； ‎ ‎（2）问点A出发后多少秒两圆相切？ ‎ ‎ ‎ P B C D T N M A K ‎(第27题图)‎ ‎8 如图，在△ABC中，∠BAC＝90°，BM平分∠ABC交AC于M，以A为圆心，‎ AM为半径作⊙A交BM于N，AN的延长线交BC于D，直线AB交⊙A于P、K 两点，作MT⊥BC于T．‎ ‎(1)求证：AK＝MT；‎ ‎(2)求证：AD⊥BC；‎ C B A O F D E ‎(3)当AK＝BD时，求证：．‎ ‎9 如图，为的直径，于点，交于点，于点．‎ ‎（1）请写出三条与有关的正确结论；‎ ‎（2）当，时，求圆中阴影部分的面积．‎ A D F E O C B G ‎（第10题图）‎ ‎10 如图，已知的直径垂直于弦于点，过点作交的延长线 于点，连接并延长交于点，且．‎ ‎（1）试问：是的切线吗？说明理由；‎ ‎（2）请证明：是的中点；‎ ‎（3）若，求的长．‎ ‎11 如图11，⊙P与⊙O相交于A、B两点，⊙P经过圆心O，点C是⊙P的优 弧上任意一点（不与点A、B重合），连结AB、AC、BC、OC。‎ ‎（1）指出图中与∠ACO相等的一个角；‎ ‎（2）当点C在⊙P上什么位置时，直线CA与⊙O相切？请说明理由；‎ ‎（3）当∠ACB=60°时，两圆半径有怎样的大小关系？请说明你的理由。‎ ‎（第12题图）‎ ‎12 如图，⊙O是△ABC的外接圆，且AB=AC，点D在弧BC上运动，过点D作DE∥BC，DE交AB的延长线于点E，连结AD、BD．‎ ‎（1）求证：∠ADB=∠E；（3分）‎ ‎（2）当点D运动到什么位置时，DE是⊙O的切线？请说明理由．（3分）‎ ‎（3）当AB=5，BC=6时，求⊙O的半径．（4分）‎ ‎ 　　　　 ‎ ‎1 （1）， （1分）‎ 又，．‎ ‎． （2分）‎ 又，．‎ 为的中点． （3分）‎ ‎（2）①，为的直径，，‎ ‎． （4分）‎ 又，．‎ ‎， （5分）‎ ‎．‎ 作于，则． （6分）‎ ‎②3 （7分）‎ ‎2 证明：（1）连接DE，∵∠ABC=90°∴∠ABE=90°，‎ ‎∴AE是⊙O直径． （1分）‎ ‎∴∠ADE=90°，∴DE⊥AC． （2分）‎ 又∵D是AC的中点，∴DE是AC的垂直平分线．‎ ‎∴AE=CE． （3分） ‎ ‎（2）在△ADE和△EFA中，‎ ‎∵∠ADE=∠AEF=90°，∠DAE=∠FAE，‎ ‎∴△ADE∽△EFA． （4分）‎ ‎∴，‎ ‎∴． （5分）‎ ‎∴AE=‎2‎cm． （6分）‎ ‎（3） ∵AE是⊙O直径，EF是⊙O的切线，∴∠ADE=∠AEF=90°，‎ ‎∴Rt△ADE∽Rt△EDF．　　　∴． （7分）‎ ‎∵，AD=CD，∴CF=nCD，∴DF=（1+n）CD， ∴DE=CD． （8分）‎ 在Rt△CDE中，CE=CD+DE=CD+（CD） =（n+2）CD．‎ ‎∴CE=CD． （9分）‎ ‎∵∠CAB=∠DEC，∴sin∠CAB=sin∠DEC ===． （10‎ ‎3 A B C E D O M F 解：⑴ 连接AC，EB，则∠CAM=∠BEM. ……………1分 又∠AMC=∠EMB, ∴△AMC∽△EMB．‎ ‎∴　，即．………3分 ‎(2) ∵DC为⊙O的直径，‎ ‎∴∠DEC=90°，EC= ………………………4分 ‎∵OA=OB=4，M为OB的中点，∴AM=6，BM=2． …………………………………5分 设EM=x，则CM=7－x．代入(1),得 .‎ 解得x1=3，x2=4．但EM＞MC，∴EM=4. …………………………………………7分 ‎(3) 由(2)知，OE=EM=4．作EF⊥OB于F，则OF=MF=OB=1． ………………8分 在Rt△EOF中，EF=　 …………………………9分 ‎∴sin∠EOB=. ……………………………………………………………10分 ‎4 （1）∵是⊙O的直径，CD是⊙O的切线 ‎∠PAC＝∠OCD＝90°，显然△DOA≌△DOC 1分 ‎∴∠DOA＝∠DOC 2分 ‎∴∠APC＝∠COD 3分 ‎ 4分 ‎（2）由，得 6分 ‎， 7分 ‎（3）若是一个等边三角形，则 8分 于是，可得，‎ 故，当时，是一个等边三角形 10分 ‎5 解：（1）所在直线与小圆相切，‎ 理由如下：过圆心作，垂足为，‎ C B O A D E 是小圆的切线，经过圆心，‎ ‎，又平分．‎ ‎．‎ 所在直线是小圆的切线．‎ ‎（2）‎ 理由如下：连接．‎ 切小圆于点，切小圆于点，‎ ‎．‎ 在与中，‎ ‎，‎ ‎（HL） ．‎ ‎，．‎ ‎（3），．‎ ‎，．‎ 圆环的面积 又， ．‎ 说明：若第（1）、（2）题中结论已证出，但在证明前未作判断的不扣分．‎ ‎6 （1） 证明：由已知DE⊥DB，⊙O是Rt△BDE的外接圆，∴BE是⊙O的直径，点O是BE的中点，连结OD， 1分 ‎∵，∴．‎ 又∵BD为∠ABC的平分线，∴．‎ ‎∵，∴．‎ ‎∴，即∴ 4分 又∵OD是⊙O的半径，‎ ‎∴AC是⊙O的切线． 5分 ‎ （2） 解：设⊙O的半径为r， ‎ 在Rt△ABC中， ，‎ ‎∴ 7分 ‎∵，，∴△ADO∽△ACB．‎ ‎∴．∴．‎ ‎∴．∴ 10分 又∵BE是⊙O的直径．∴．∴△BEF∽△BAC ‎∴．‎ ‎7 解：（1）当0≤t≤5.5时，函数表达式为d＝11-2t； 　 …………………………1分 当t＞5.5时，函数表达式为d＝2t -11．　　 ……………………………………2分 ‎（2）两圆相切可分为如下四种情况： ‎ ‎①当两圆第一次外切，由题意，可得11－2t＝1＋1＋t，t＝3； …………………4分 ‎②当两圆第一次内切，由题意，可得11－2t＝1＋t－1，t＝； ……………6分 ‎③当两圆第二次内切，由题意，可得2t－11＝1＋t－1，t＝11； ………………8分 ‎④当两圆第二次外切，由题意，可得2t－11＝1＋t＋1，t＝13． ‎ 所以，点A出发后3秒、秒、11秒、13秒两圆相切． ……………………10分 ‎8 证明：(1)∵BM平分∠ABC，∠BAC＝90°，MT⊥BC，‎ ‎∴AM＝MT．又∵AM＝AK，∴AK＝MT．‎ ‎(2)∵BM平分∠ABC，∴∠ABM＝∠CBM．‎ ‎∵AM＝AN，∴∠AMN＝∠ANM 又∵∠ANM＝∠BND，∴∠AMN＝∠BND．‎ ‎∵∠BAC＝90°，∴∠ABM＋∠AMB＝90°‎ ‎∴∠CBM＋∠BND＝90°，∴∠BDN＝90°．‎ ‎∴AD⊥BC ‎(3)∵BNM和BPK为⊙A的割线，∴BN·BM＝BP·BK，∴‎ ‎∵AK＝BD，AK＝MT，∴BD＝MT ‎∵AD⊥BC，MT⊥BC，∴∠ADB＝∠MTC＝90°，∴∠C＋∠CMT＝90°‎ ‎∵∠BAC＝90°，∴∠C＋∠ABC＝90°，∴∠ABC＝∠CMT 在△ABD和△CMT中，‎ ‎∴△ABD≌△CMT，∴AB＝MC ‎∵AK＝AM，∴AB＋AK＝MC＋AM，即BK＝AC ‎∴‎ ‎9 解：（1）答案不唯一，只要合理均可．例如：‎ ‎①；②；③；④；⑤；⑥；⑦是直角三角形；⑧是等腰三角形． 3分 C B A O F D E ‎（2）连结，则．‎ ‎，，． 4分 为的直径，．‎ 在中，，，． 5分 ‎，．‎ ‎，是的中位线．‎ ‎．‎ ‎． 6分 ‎． 7分 ‎． 8分 ‎10 （1）解：是的切线 1分 理由：‎ 即．‎ 是的切线． 2分 A D F E O C B G ‎（第19题图1）‎ ‎（2）第一种方法：‎ 证明：连接，如图（第19题图1）‎ ‎，‎ 且过圆心 ‎，‎ 是等边三角形． 3分 ‎ 4分 在中，‎ D F E O C B G ‎（第19题图2）‎ A 点为的中点 5分 第二种方法：‎ 证明：连接，如图（第19题图2）‎ 为的直径 又 ‎ 3分 且过圆心 ‎ 4分 点为的中点． 5分 ‎（3）解：‎ 又 ‎ 6分 ‎ 7分 ‎ 8分 ‎11 （1）∠BCO；‎ ‎（2）连接OP，并延长与⊙P交于点D，‎ 若点C在点D位置时，直线CA与⊙O相切 理由：连接AD，OA 则∠DAO=90°，‎ 即OA⊥DA 所以DA与与⊙O相切 即点C在点D位置时，直线CA与⊙O相切 ‎（3）当∠ACB=60°时，两圆半径相等 理由：∠ADB=∠ACB=60°‎ 又因为∠ADO=∠BDO 所以∠ADO=30°‎ 因为∠DAO=90°‎ 所以OA=OD 即OA=PO 所以当∠ACB=60°时，两圆半径相等 ‎12 解：（1）在△ABC中，∵AB=AC，‎ ‎∴∠ABC=∠C． 1分 ‎ ∵DE∥BC，∴∠ABC=∠E，‎ ‎ ∴∠E=∠C． 2分 又∵∠ADB=∠C， ‎ ‎　　　　　∴∠ADB=∠E． 3分 ‎（2）当点D是弧BC的中点时，DE是⊙O的切线． 4分 理由是：当点D是弧BC的中点时，则有AD⊥BC，且AD过圆心O． 5分 ‎ 又∵DE∥BC，∴ AD⊥ED． ‎ ‎ ∴ DE是⊙O的切线． 6分 ‎ （3）连结BO、AO，并延长AO交BC于点F， ‎ ‎ 则AF⊥BC，且BF=BC=3． 7分 ‎ 又∵AB=5，∴AF=4． 8分 ‎ 设⊙O的半径为，在Rt△OBF中，OF=4－，OB=，BF=3， ‎ ‎　　　　　　∴　＝3＋（4－） 9分 ‎ 解得＝， ∴⊙O的半径是． 10分 ‎23、解：（1）△CDA≌△DCE，△BAD≌△DCE； 2分