中考专题中线倍长法及截长补短 10页

几何证明中常用辅助线 (一)中线倍长法: 例 1 、求证：三角形一边上的中线小于其他两边和的一半。 已知：如图，△ABC 中，AD 是 BC 边上的中线，求证：AD ﹤ (AB+AC) 分析：要证明 AD ﹤ (AB+AC)，就是证明 AB+AC>2AD，也就是证明两条线 段之和大于第三条线段，而我们只能用“三角形两边之和大于第三边”，但题中 的三条线段共点，没有构成一个三角形，不能用三角形三边关系定理，因此应该 进行转化。待证结论 AB+AC>2AD 中，出现了 2AD，即中线 AD 应该加倍。 证明：延长 AD 至 E，使 DE=AD，连 CE，则 AE=2AD。 在△ADB 和△EDC 中， ∴△ADB≌△EDC(SAS) ∴AB=CE 又 在△ACE 中， AC+CE＞AE ∴AC+AB＞2AD，即 AD ﹤ (AB+AC) 小结：(1)涉及三角形中线问题时，常采用延长中线一倍的办法，即中线倍长法。 它可以将分居中线两旁的两条边 AB、AC 和两个角∠BAD 和∠CAD 集中于同一 个三角形中，以利于问题的获解。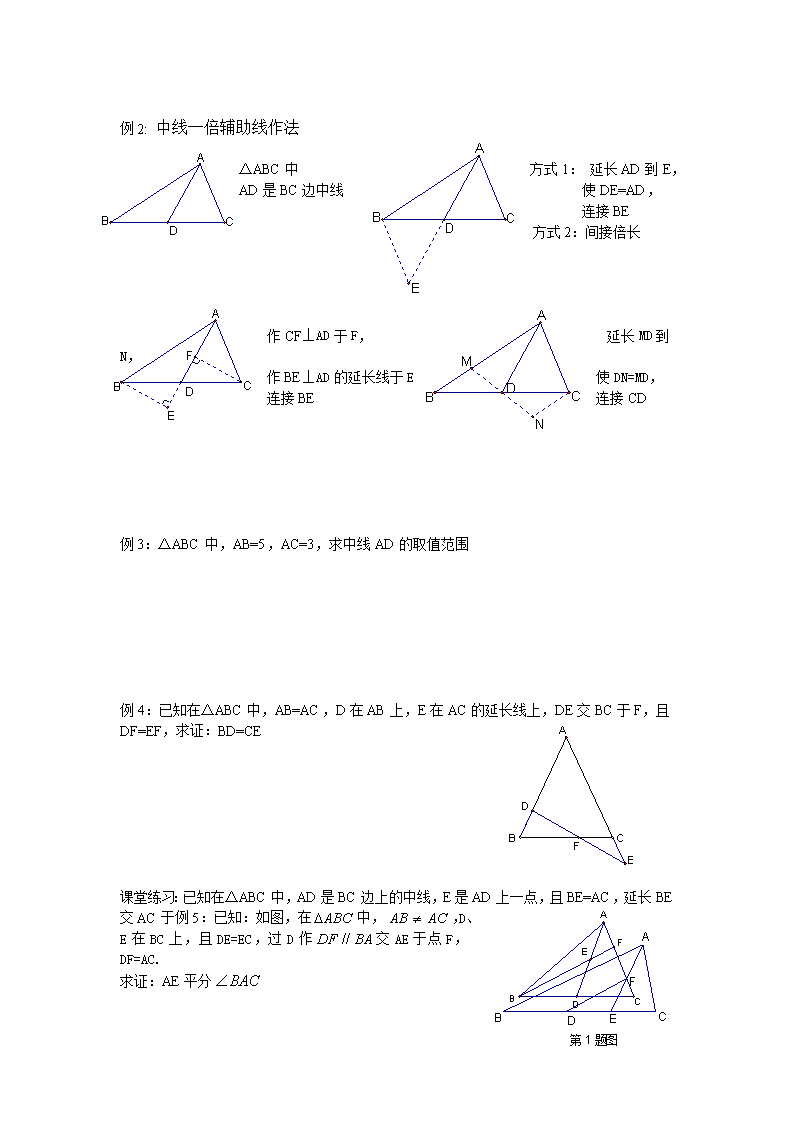 课题练习: 中，AD 是 的平分线，且 BD=CD，求证 AB=AC      AD= DE ∠ADB= ∠EDC BD= DC 2 1 2 1 2 1 ABC∆ BAC∠ B CD A E C D A B 例 2: 中线一倍辅助线作法 △ABC 中 方式 1： 延长 AD 到 E， AD 是 BC 边中线 使 DE=AD， 连接 BE 方式 2：间接倍长 作 CF⊥AD 于 F， 延长 MD 到 N， 作 BE⊥AD 的延长线于 E 使 DN=MD， 连接 BE 连接 CD 例 3：△ABC 中，AB=5，AC=3，求中线 AD 的取值范围 例 4：已知在△ABC 中，AB=AC，D 在 AB 上，E 在 AC 的延长线上，DE 交 BC 于 F，且 DF=EF，求证：BD=CE 课堂练习：已知在△ABC 中，AD 是 BC 边上的中线，E 是 AD 上一点，且 BE=AC，延长 BE 交 AC 于例 5：已知：如图，在 中， ，D、 E 在 BC 上，且 DE=EC，过 D 作 交 AE 于点 F， DF=AC. 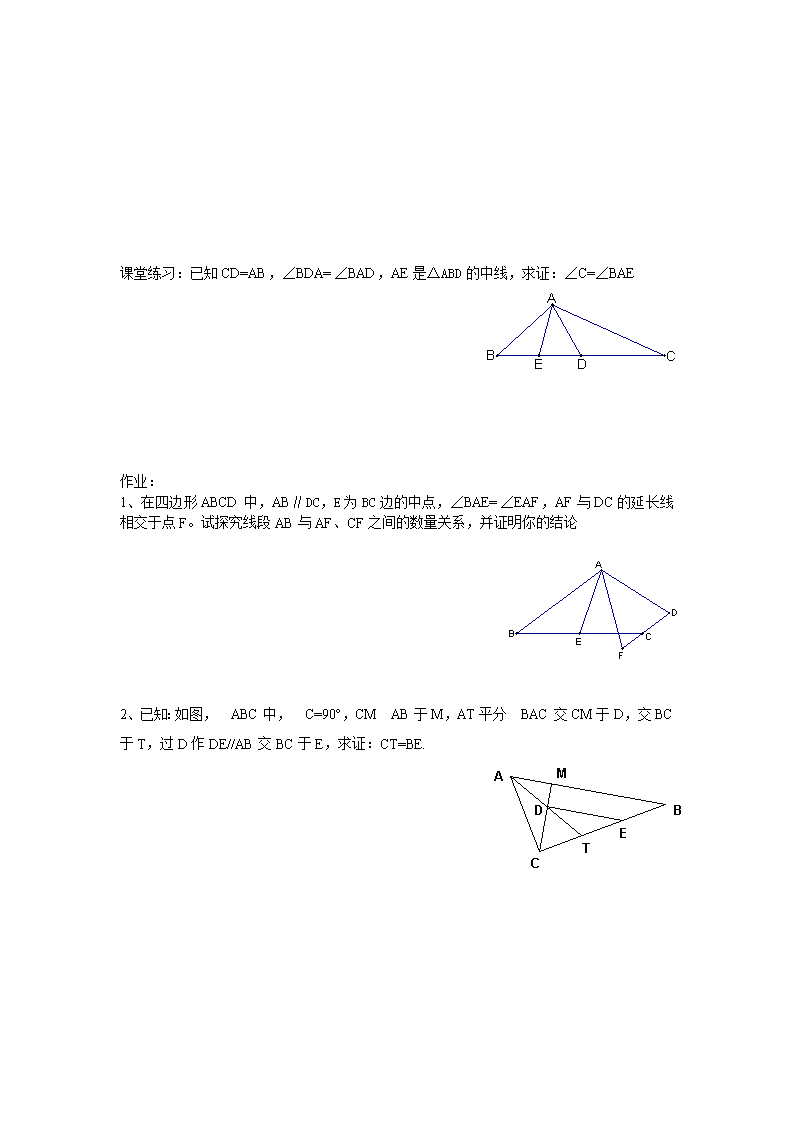求证：AE 平分 ABC∆ ACAB ≠ BADF // BAC∠ D A B C E D A B C F E D CB A N D CB A M F E D A B C F E C A B D 第 1 题图 A B F D E C 课堂练习：已知 CD=AB，∠BDA=∠BAD，AE 是△ABD 的中线，求证：∠C=∠BAE 作业： 1、在四边形 ABCD 中，AB∥DC，E 为 BC 边的中点，∠BAE=∠EAF，AF 与 DC 的延长线 相交于点 F。试探究线段 AB 与 AF、CF 之间的数量关系，并证明你的结论 2、已知：如图，ABC 中，C=90°，CMAB 于 M，AT 平分BAC 交 CM 于 D，交 BC 于 T，过 D 作 DE//AB 交 BC 于 E，求证：CT=BE. E D A B C F E A B C D D A B C M T E 3：已知在△ABC 中，AD 是 BC 边上的中线，E 是 AD 上一点，且 BE=AC，延长 BE 交 AC 于 F，求证：AF=EF 4：已知 CD=AB，∠BDA=∠BAD，AE 是△ABD 的中线，求证：∠C=∠BAE 5、在四边形 ABCD 中，AB∥DC，E 为 BC 边的中点，∠BAE=∠EAF，AF 与 DC 的延长线 相交于点 F。试探究线段 AB 与 AF、CF 之间的数量关系，并证明你的结论 （二）截长补短法 例1. 已知，如图 1-1，在四边形 ABCD 中，BC＞AB，AD=DC，BD 平分∠ ABC. 求证：∠BAD+∠BCD=180°. 分析：因为平角等于 180°，因而应考虑把两个不在一起的通过全等转 化成为平角，图中缺少全等的三角形，因而解题的关键在于构造直角三角形， 可通过“截长补短法”来实现. 证明：过点 D 作 DE 垂直 BA 的延长线于点 E，作 DF⊥BC 于点 F，如图 1-2 ∵BD 平分∠ABC，∴DE=DF， F E D A B C E D A B C F E A B C D A B C D 图 1-1 F E D CB A 图 1-2 A D B C E 图 2-1 在 Rt△ADE 与 Rt△CDF 中， ∴Rt△ADE≌Rt△CDF(HL),∴∠DAE=∠DCF. 又∠BAD+∠DAE=180°，∴∠BAD+∠DCF=180°， 即∠BAD+∠BCD=180° 例2. 如图 2-1，AD∥BC，点 E 在线段 AB 上，∠ADE=∠CDE，∠DCE=∠ECB. 求证：CD=AD+BC. 例3. 已知，如图 3-1，∠1=∠2，P 为 BN 上一点，且 PD⊥BC 于点 D，AB+BC=2BD. 求证：∠BAP+∠BCP=180°.    = = CDAD DFDE A B CD P 1 2 N 图 3-1 例4. 已知：如图 4-1，在△ABC 中，∠C＝2∠B，∠1＝∠2. 求证：AB=AC+CD. 作业： 1、已知：如图，ABCD 是正方形，∠FAD=∠FAE. 求证：BE+DF=AE. 2、五边形 ABCDE 中，AB=AE，BC+DE=CD，∠ABC+∠AED=180°，求证：AD 平分∠CDE D CB A 1 2 图 4-1 F E D CB A （三）其它几种常见的形式： 1、有角平分线时，通常在角的两边截取相等的线段，构造全 等三角形。 例：如图 1：已知 AD 为△ABC 的中线，且∠1＝∠2,∠3＝∠4,求证： BE＋CF＞EF。 2、有以线段中点为端点的线段时，常延长加倍此线段，构造全 等三角形。 例：：如图 2：AD 为△ABC 的中线，且∠1＝∠2，∠3＝∠4，求证：BE＋CF＞ EF C E D B A A B CD E F N 1图 1 2 3 4 2图 A B C D E F M 1 2 3 4 练习：已知△ABC，AD 是 BC 边上的中线，分别以 AB 边、AC 边为直角边各 向形外作等腰直角三角形，如图 4， 求证 EF＝2AD。 3、延长已知边构造三角形： 例如：如图 6：已知 AC＝BD，AD⊥AC 于 A ，BC⊥BD 于 B， 求证：AD＝BC 4、连接四边形的对角线，把四边形的问题转化成为三角形来解 决。 例如：如图 7：AB∥CD，AD∥BC 求证：AB=CD。 A B CD E F 4图 A B CD E 6图 O A B C D 7图 1 2 3 4 5、有和角平分线垂直的线段时，通常把这条线段延长。 例如：如图 8：在 Rt△ABC 中，AB＝AC，∠BAC＝90°，∠1＝∠2，CE⊥BD 的延长于 E 。求证：BD＝2CE 6 连接已知点，构造全等三角形。 例如：已知：如图 9；AC、BD 相交于 O 点，且 AB＝DC，AC＝BD，求证：∠A ＝∠D。 九、取线段中点构造全等三有形。 例如：如图 10：AB＝DC，∠A＝∠D 求证：∠ABC＝∠DCB。 D CB A 110 −图 O 10图 D CB A M N