2009年福建省厦门市中考数学试题及答案 11页

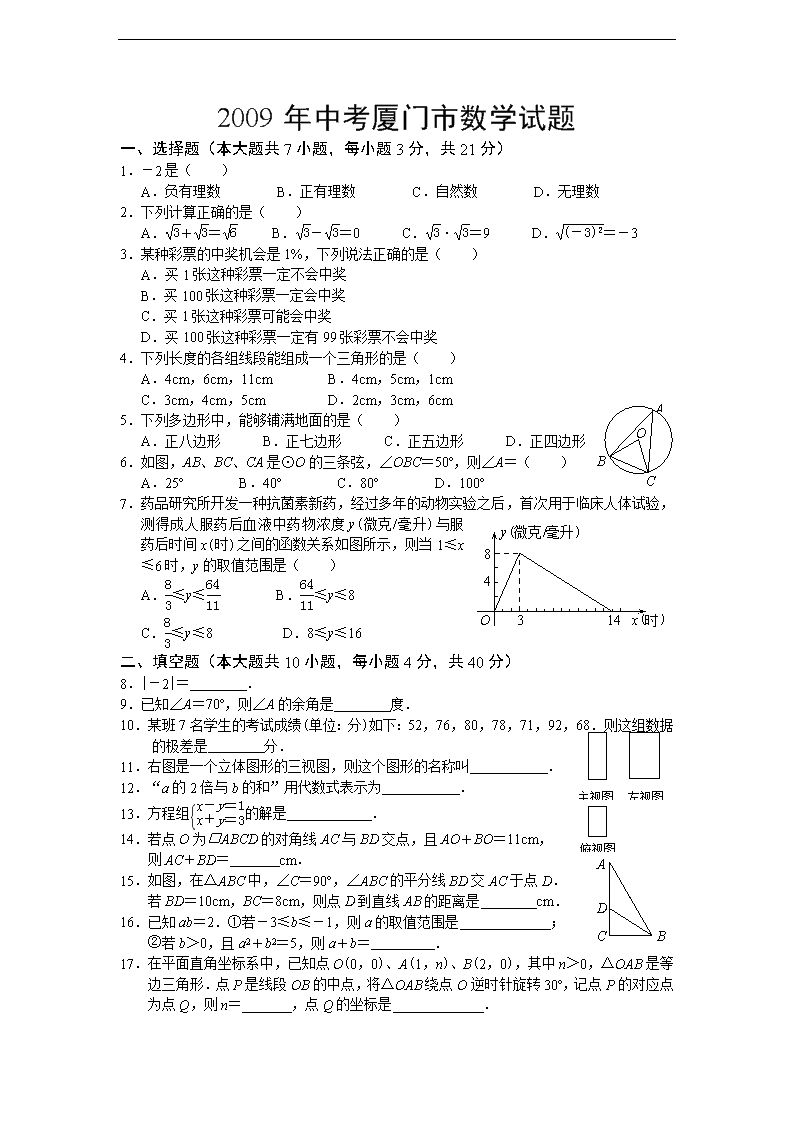
‎2009年中考厦门市数学试题 一、选择题（本大题共7小题，每小题3分，共21分）‎ ‎1．－2是（ ）‎ A．负有理数 B．正有理数 C．自然数 D．无理数 ‎2．下列计算正确的是（ ）‎ A．＋＝ B．－＝‎0 C．·＝9 D．＝－3‎ ‎3．某种彩票的中奖机会是1%，下列说法正确的是（ ）‎ A．买1张这种彩票一定不会中奖 B．买100张这种彩票一定会中奖 C．买1张这种彩票可能会中奖 D．买100张这种彩票一定有99张彩票不会中奖 ‎4．下列长度的各组线段能组成一个三角形的是（ ）‎ A．‎4cm，‎6cm，‎11cm B．‎4cm，‎5cm，‎‎1cm A B C O C．‎3cm，‎4cm，‎5cm D．‎2cm，‎3cm，‎‎6cm ‎5．下列多边形中，能够铺满地面的是（ ）‎ A．正八边形 B．正七边形 C．正五边形 D．正四边形 ‎6．如图，AB、BC、CA是⊙O的三条弦，∠OBC＝50º，则∠A＝（ ）‎ A．25º B．40º C．80º D．100º O y(微克/毫升)‎ x(时)‎ ‎3‎ ‎14‎ ‎8‎ ‎4‎ ‎7．药品研究所开发一种抗菌素新药，经过多年的动物实验之后，首次用于临床人体试验，测得成人服药后血液中药物浓度y(微克/毫升)与服药后时间x(时)之间的函数关系如图所示，则当1≤x≤6时，y的取值范围是（ ）‎ A．≤y≤ B．≤y≤8‎ C．≤y≤8 D．8≤y≤16‎ 二、填空题（本大题共10小题，每小题4分，共40分）‎ ‎8．|－2|＝ ．‎ ‎9．已知∠A＝70º，则∠A的余角是 度．‎ 主视图 左视图 俯视图 ‎10．某班7名学生的考试成绩(单位：分)如下：52，76，80，78，71，92，68．则这组数据的极差是 分．‎ ‎11．右图是一个立体图形的三视图，则这个图形的名称叫 ．‎ ‎12．“a的2倍与b的和”用代数式表示为 ．‎ ‎13．方程组的解是 ．‎ ‎14．若点O为□ABCD的对角线AC与BD交点，且AO＋BO＝‎11cm，‎ C B A D 则AC＋BD＝ cm．‎ ‎15．如图，在△ABC中，∠C＝90º，∠ABC的平分线BD交AC于点D．‎ 若BD＝‎10cm，BC＝‎8cm，则点D到直线AB的距离是 cm．‎ ‎16．已知ab＝2．①若－3≤b≤－1，则a的取值范围是 ；‎ ‎②若b＞0，且a2＋b2＝5，则a＋b＝ ．‎ ‎17．在平面直角坐标系中，已知点O(0，0)、A(1，n)、B(2，0)，其中n＞0，△OAB是等边三角形．点P是线段OB的中点，将△OAB绕点O逆时针旋转30º，记点P的对应点为点Q，则n＝ ，点Q的坐标是 ．‎ 三、解答题（本大题共9小题，共89分）‎ ‎18．(本题满分18分)‎ ‎(1)计算：(－1)2÷＋(7－3)×－()0；‎ ‎(2)计算：[(2x－y)(2x＋y)＋y(y－6x)]÷2x；‎ ‎(3)解方程：x2－6x＋1＝0．‎ ‎19．(8分)掷两枚普通的正六面体骰子，所得点数之和的所有可能如下表所示：‎ 第1枚 和 第2枚 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎(1)求出点数之和是11的概率；‎ ‎(2)你认为最有可能出现的点数之和是多少？请说明理由．‎ A B D C ‎20．(8分)已知：在△ABC中，AB＝AC．‎ ‎(1)设△ABC的周长为7，BC＝y，AB＝x(2≤x≤3)．‎ 写出y关于x的函数关系式，并在直角坐标系中 画出此函数的图象；‎ ‎(2)如图，D是线段BC上一点，连接AD．若∠B＝∠BAD，求证：△ABC∽△DBA．‎ ‎21．(8分)如图，已知梯形ABCD，AD∥BC，AF交CD于E，交BC的延长线于F．‎ ‎(1)若∠B＋∠DCF＝180º，求证：四边形ABCD是等腰梯形；‎ ‎(2)若E是线段CD的中点，且CF∶CB＝1∶3，AD＝6，求梯形ABCD中位线的长．‎ A B F E D C ‎22．(8分)供电局的电力维修工甲、乙两人要到45千米远的A地进行电力抢修．甲骑摩托车先行，t(t≥0)小时后乙开抢修车载着所需材料出发．‎ ‎(1)若t＝(小时)，抢修车的速度是摩托车的1.5倍，且甲、乙两人同时到达，求摩托车的速度；‎ ‎(2)若摩托车的速度是‎45千米/小时，抢修车的速度是‎60千米/小时，且乙不能比甲晚到则t的最大值是多少？‎ ‎23．(9分)已知四边形ABCD，AD∥BC，连接BD．‎ ‎(1)小明说：“若添加条件BD2＝BC2＋CD2，则四边形ABCD是矩形．”你认为小明的说法是否正确？若正确，请说明理由；若不正确，请举出一个反例说明．‎ ‎(2)若BD平分∠ABC，∠DBC＝∠BDC，tan∠DBC＝1，求证：四边形ABCD是正方形．‎ A O B D C P ‎24．(9分)如图，已知AB是⊙O的直径，点C在⊙O上，‎ P是△OAC的重心，且OP＝，∠A＝30º．‎ ‎(1)求劣弧的长；‎ ‎(2)若∠ABD＝120º，BD＝1，求证：CD是⊙O的切线．‎ ‎25．(9分)我们知道，当一条直线与一个圆有两个公共点时，称这条直线与这个圆相交．类似地，我们定义：当一条直线与一个正方形有两个公共点时，称这条直线与这个正方形相交．‎ 如图，在平面直角坐标系中，正方形OABC的顶点为O(0，0)、A(1，0)、B(1，1)、C(0，1)．‎ ‎(1)判断直线y＝x＋与正方形OABC是否相交，并说明理由；‎ C B O A x y ‎(2)设d是点O到直线y＝－x＋b的距离，若直线y＝－x＋b与正方形OABC相交，求d的取值范围．‎ ‎26．(11分)已知二次函数y＝x2－x＋c．‎ ‎(1)若点A(－1，a)、B(2，2n－1)在二次函数y＝x2－x＋c的图象上，求此二次函数的最小值；‎ ‎(2)若点D(x1，y1)、E(x2，y2)、P(m，n)(m＞n)在二次函数y＝x2－x＋c的图象上，且D、E两点关于坐标原点成中心对称，连接OP．当2≤OP≤2＋时，试判断直线DE与抛物线y＝x2－x＋c＋的交点个数，并说明理由．‎ 厦门市2009年初中毕业及高中阶段各类学校招生考试 数学参考答案及评分标准 说明：‎ ‎1．解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照解答中评分标准相应评分；‎ ‎2．评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅．如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影响的程度决定后继部分的给分，但原则上不超过后继部分应得分数的一半；‎ ‎3．解答题评分时，给分或扣分均以1分为基本单位．‎ 一、选择题(本大题有7小题，每小题3分，共21分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 选项 A B C ‎ C D B C 二、填空题(本大题有10小题，每小题4分，共40分)‎ ‎8. 2. 9‎‎. 20度. 10. 40分. 11.长方体(四棱柱). 12. ‎2a＋b. 13. ‎14. 22厘米. 15. 6厘米. 16. (1) －2≤a≤－ ；(2) 3 . 17. ；(，).‎ 三、解答题(本大题有9小题，共89分)‎ ‎18. (本题满分18分) ‎ ‎(1)解：(－1)2÷＋(7－3)×－()0‎ ‎ ＝1×2＋4×－1 ……4分 ‎ ＝2＋3－1 ……5分 ‎ ＝4. ……6分 ‎(2)解：[(2x－y)( 2x＋y)＋y(y－6x)]÷2x ‎ ＝(4x2－y2＋y2－6xy)÷2x ……10分 ‎ ＝(4x2－6xy)÷2x ……11分 ‎ ＝2x－3y. ……12分 ‎(3)解法1：x2－6x＋1＝0‎ ‎ ∵ b2－‎4ac＝(－6)2－4＝32 ……13分 ‎∴ x＝ ……14分 ‎ ＝ ……15分 ‎ ＝3±2. ……16分 ‎ 即x1＝3＋2，x2＝3－2. ……18分 ‎ 解法2：x2－6x＋1＝0‎ ‎ (x－3)2－8＝0 ……14分 ‎ (x－3)2 ＝8 ……15分 ‎ x－3＝±2 ……16分 ‎ 即x1＝3＋2，x2＝3－2. ……18分 ‎19．(本题满分8分)‎ ‎(1)解：P(点数之和是11)＝＝. ……4分 ‎(2)解：最有可能出现的点数之和是7. ……6分 ‎ ∵ 在所有可能出现的点数之和中，7是众数. ……8分 ‎ 或： P(点数之和是7)＝， ……7分 ‎ 是所有可能出现的点数之和的概率的最大值. ……8分 ‎20．(本题满分8分)‎ ‎(1)解：y＝7－2x(2≤x≤3) ……1分 ‎ 画直角坐标系 ……2分 ‎ 画线段 ……4分 ‎(2)证明：∵ AB＝AC，∴ ∠B＝∠C. ……5分 ‎ ∵ ∠B＝∠BAD，∴ ∠BAD＝∠C. ……6分 ‎ 又∵ ∠B＝∠B， ……7分 ‎ ∴ △BAC∽△BDA. ……8分 ‎ 21．(本题满分8分)‎ ‎(1)∵ ∠DCB＋∠DCF＝180°， ……1分 ‎ 又∵ ∠B＋∠DCF＝180°，‎ ‎ ∴ ∠B＝∠DCB. ……2分 ‎ ∵ 四边形ABCD是梯形，‎ ‎ ∴ 四边形ABCD是等腰梯形. ……3分 ‎(2)∵ AD∥BC，‎ ‎ ∴ ∠DAE＝∠F. ……4分 ‎ ∵ E是线段CD的中点，∴ DE＝CE.‎ ‎ 又∵ ∠DEA＝∠FEC，‎ ‎ ∴ △ADE≌△FCE . ……5分 ‎ ∴ AD＝CF. ……6分 ‎ ∵ CF∶BC＝1∶3，∴ AD∶BC＝1∶3.‎ ‎ ∵ AD＝6，∴ BC＝18. ……7分 ‎ ∴ 梯形ABCD的中位线是 (18＋6)÷2＝12. ……8分 ‎22．(本题满分8分)‎ ‎(1)解：设摩托车的速度是x千米/时，则抢修车的速度是1.5x千米/时. ‎ ‎ 由题意得 －＝， ……2分 ‎ 解得x＝40. ……3分 ‎ 经检验，x＝40千米/时是原方程的解且符合题意.‎ ‎ 答：摩托车的速度为40千米/时. ……4分 ‎(2)解：法1：由题意得t＋≤， ……6分 ‎ 解得t≤. ∴ 0≤t≤. ……7分 ‎ 法2：当甲、乙两人同时到达时，由题意得t＋＝， ……5分 ‎ 解得t＝. ……6分 ‎ ∵ 乙不能比甲晚到，∴ t≤. ……7分 ‎ ∴ t最大值是 (时)；或：答：乙最多只能比甲迟 (时)出发. ……8分 ‎ 23．(本题满分9分)‎ ‎ (1)解： 不正确. ……1分 ‎ 如图作(直角)梯形ABCD， ……2分 ‎ 使得AD∥BC，∠C＝90°. ‎ ‎ 连结BD，则有BD2＝BC2＋CD2. ……3分 ‎ 而四边形ABCD是直角梯形不是矩形. ……4分 ‎ (2)证明：如图，‎ ‎ ∵ tan∠DBC＝1，‎ ‎ ∴ ∠DBC＝45°. ……5分 ‎ ∵ ∠DBC＝∠BDC，‎ ‎ ∴ ∠BDC＝45°.‎ ‎ 且BC＝DC. ……6分 ‎ 法1： ∵ BD平分∠ABC，‎ ‎ ∴ ∠ABD＝45°，∴ ∠ABD＝∠BDC.‎ ‎ ∴ AB∥DC.‎ ‎ ∴ 四边形ABCD是平行四边形. ……7分 ‎ 又∵ ∠ABC＝45°＋45°＝90°，‎ ‎ ∴ 四边形ABCD是矩形. ……8分 ‎ ∵ BC＝DC，‎ ‎ ∴ 四边形ABCD是正方形. ……9分 ‎ 法2：∵ BD平分∠ABC， ∠BDC＝45°，∴∠ABC＝90°.‎ ‎ ∵ ∠DBC＝∠BDC＝45°，∴∠BCD＝90°.‎ ‎ ∵ AD∥BC，‎ ‎ ∴ ∠ADC＝90°. ……7分 ‎ ∴ 四边形ABCD是矩形. ……8分 ‎ 又∵ BC＝DC ‎ ∴ 四边形ABCD是正方形. ……9分 ‎ 法3：∵ BD平分∠ABC，∴ ∠ABD＝45°. ∴ ∠BDC＝∠ABD.‎ ‎ ∵ AD∥BC，∴ ∠ADB＝∠DBC.‎ ‎ ∵ BD＝BD，‎ ‎ ∴ △ADB≌△CBD.‎ ‎ ∴ AD＝BC＝DC＝AB. ……7分 ‎ ∴ 四边形ABCD是菱形. ……8分 ‎ 又∵∠ABC＝45°＋45°＝90°，‎ ‎ ∴ 四边形ABCD是正方形. ……9分 ‎24．(本题满分9分)‎ ‎(1)解：延长OP交AC于E，‎ ‎ ∵ P是△OAC的重心，OP＝，‎ ‎ ∴ OE＝1， ……1分 ‎ 且 E是AC的中点.‎ ‎ ∵ OA＝OC，∴ OE⊥AC.‎ ‎ 在Rt△OAE中，∵ ∠A＝30°，OE＝1，‎ ‎ ∴ OA＝2. ……2分 ‎ ∴ ∠AOE＝60°. ‎ ‎ ∴ ∠AOC＝120°. ……3分 ‎ ∴ ＝π. ……4分 ‎(2)证明：连结BC.‎ ‎ ∵ E、O分别是线段AC、AB的中点，‎ ‎ ∴ BC∥OE，且BC＝2OE＝2＝OB＝OC. ‎ ‎ ∴ △OBC是等边三角形. ……5分 ‎ 法1：∴ ∠OBC＝60°.‎ ‎ ∵ ∠OBD＝120°，∴ ∠CBD＝60°＝∠AOE. ……6分 ‎ ∵ BD＝1＝OE，BC＝OA，‎ ‎ ∴ △OAE ≌△BCD. ……7分 ‎ ∴ ∠BCD＝30°.‎ ‎ ∵ ∠OCB＝60°，‎ ‎ ∴ ∠OCD＝90°. ……8分 ‎ ∴ CD是⊙O的切线. ……9分 ‎ 法2：过B作BF∥DC交CO于F.‎ ‎ ∵ ∠BOC＝60°，∠ABD＝120°,‎ ‎ ∴ OC∥BD. ……6分 ‎ ∴ 四边形BDCF是平行四边形. ……7分 ‎ ∴ CF＝BD＝1.‎ ‎ ∵ OC＝2，‎ ‎ ∴ F是OC的中点.‎ ‎ ∴ BF⊥OC. ……8分 ‎ ∴ CD⊥OC. ‎ ‎ ∴ CD是⊙O的切线. ……9分 ‎ 25．(本题满分10分)‎ ‎ (1)解：相交. ……2分 ‎ ∵ 直线y＝x＋与线段OC交于点(0，)同时 ……3分 ‎ 直线y＝x＋与线段CB交于点(，1)， ……4分 ‎ ∴ 直线y＝x＋与正方形OABC相交.‎ ‎(2)解：当直线y＝－x＋b经过点B时，‎ ‎ 即有 1＝－＋b，‎ ‎ ∴ b＝＋1. ‎ ‎ 即 y＝－x＋1＋. ……5分 ‎ 记直线y＝－x＋1＋与x、y轴的交点分别为D、E.‎ ‎ 则D(，0)，E(0，1＋). ……6分 ‎ 法1：在Rt△BAD中，tan∠BDA＝ ＝＝，‎ ‎ ∴ ∠EDO＝60°， ∠OED＝30°.‎ ‎ 过O作OF1⊥DE，垂足为F1，则OF1＝d1. ……7分 ‎ 在Rt△OF1E中，∵ ∠OED＝30°，‎ ‎ ∴ d1＝. ……8分 ‎ 法2：∴ DE＝(3＋).‎ ‎ 过O作OF1⊥DE，垂足为F1，则OF1＝d1. ……7分 ‎ ∴ d1＝×(1＋)÷(3＋)‎ ‎ ＝. ……8分 ‎ ∵ 直线y＝－x＋b与直线y＝－x＋1＋平行.‎ ‎ 法1：当直线y＝－x＋b与正方形OABC相交时，一定与线段OB相交，且交点不与 ‎ 点O、 B重合.故直线y＝－x＋b也一定与线段OF1相交，记交点为F，则 F不与 点O、 F1重合，且OF＝d. ……9分 ‎ ∴ 当直线y＝－x＋b与正方形相交时，‎ ‎ 有 0＜d＜. ……10分 ‎ 法2：当直线y＝－x＋b与直线y＝x(x＞0)相交时，‎ ‎ 有 x＝－x＋b，即x＝.‎ ‎ ① 当0＜b＜1＋时，0＜x＜1， 0＜y＜1.‎ ‎ 此时直线y＝－x＋b与线段OB相交，且交点不与点O、 B重合.‎ ‎ ② 当b＞1＋时，x＞1，‎ ‎ 此时直线y＝－x＋b与线段OB不相交.‎ ‎ 而当b≤0时，直线y＝－x＋b不经过第一象限，即与正方形OABC不相交.‎ ‎ ∴ 当0＜b＜1＋时，直线y＝－x＋b与正方形OABC相交. ……9分 ‎ 此时有0＜d＜. ……10分 ‎ 26．(本题满分11分)‎ ‎ (1)解：法1：由题意得 ……1分 ‎ 解得 ……2分 ‎ 法2：∵ 抛物线y＝x2－x＋c的对称轴是x＝， ‎ ‎ 且 －(－1) ＝2－，∴ A、B两点关于对称轴对称. ‎ ‎ ∴ n＝2n－1 ……1分 ‎ ∴ n＝1，c＝－1. ……2分 ‎ ∴ 有 y＝x2－x－1 ……3分 ‎ ＝(x－)2－. ‎ ‎ ∴ 二次函数y＝x2－x－1的最小值是－. ……4分 ‎ ‎ (2)解：∵ 点P(m，m)(m＞0)，‎ ‎ ∴ PO＝m.‎ ‎ ∴ 2≤m ≤＋2.‎ ‎ ∴ 2≤m≤1＋. ……5分 ‎ 法1： ∵ 点P(m，m)(m＞0)在二次函数y＝x2－x＋c的图象上，‎ ‎ ∴ m＝m2－m＋c，即c＝－m2＋‎2m.‎ ‎ ∵ 开口向下，且对称轴m＝1，‎ ‎ ∴ 当2≤m≤1＋ 时， ‎ ‎ 有 －1≤c≤0. ……6分 ‎ 法2：∵ 2≤m≤1＋，‎ ‎ ∴ 1≤m－1≤.‎ ‎ ∴ 1≤(m－1)2≤2. ‎ ‎ ∵ 点P(m，m)(m＞0)在二次函数y＝x2－x＋c的图象上，‎ ‎ ∴ m＝m2－m＋c，即1－c＝(m－1)2.‎ ‎ ∴ 1≤1－c≤2.‎ ‎ ∴ －1≤c≤0. ……6分 ‎ ∵ 点D、E关于原点成中心对称，‎ ‎ 法1： ∴ x2＝－x1，y2＝－y1.‎ ‎ ∴ ‎ ∴ 2y1＝－2x1， y1＝－x1. ‎ ‎ 设直线DE：y＝kx.‎ ‎ 有 －x1＝kx1.‎ ‎ 由题意，存在x1≠x2. ‎ ‎ ∴ 存在x1，使x1≠0. ……7分 ‎ ∴ k＝－1.‎ ‎ ∴ 直线DE： y＝－x. ……8分 ‎ 法2：设直线DE：y＝kx.‎ ‎ 则根据题意有 kx＝x2－x＋c，即x2－(k＋1) x＋c＝0.‎ ‎ ∵ －1≤c≤0，‎ ‎ ∴ (k＋1)2－‎4c≥0.‎ ‎ ∴ 方程x2－(k＋1) x＋c＝0有实数根. ……7分 ‎ ∵ x1＋x2＝0， ‎ ‎ ∴ k＋1＝0.‎ ‎ ∴ k＝－1.‎ ‎ ∴ 直线DE： y＝－x. ……8分 ‎ 若 则有 x2＋c＋＝0.即 x2＝－c－.‎ ‎ ① 当 －c－＝0时，即c＝－时，方程x2＝－c－有相同的实数根，‎ ‎ 即直线y＝－x与抛物线y＝x2－x＋c＋有唯一交点. ……9分 ‎ ② 当 －c－＞0时，即c＜－时，即－1≤c＜－时，‎ ‎ 方程x2＝－c－有两个不同实数根，‎ ‎ 即直线y＝－x与抛物线y＝x2－x＋c＋有两个不同的交点. ……10分 ‎ ③ 当 －c－＜0时，即c＞－时，即－＜c≤0时，‎ ‎ 方程x2＝－c－没有实数根，‎ ‎ 即直线y＝－x与抛物线y＝x2－x＋c＋没有交点. ……11分