2019年中考数学提分训练 轴对称（含解析） 新版新人教版 21页

‎2019年中考数学提分训练: 轴对称 一、选择题 ‎1.在以下永洁环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形的是（   ） ‎ A.                  B.                  C.                  D. ‎ ‎2.小狗皮皮看到镜子里的自己,觉得很奇怪,此时它所看到的全身像是（   ） ‎ A.                        B.                         C.                         D. ‎ 21‎ ‎3.如图，正方形OABC对角线交点为D，过D的直线分别交AB，OC于E，F，已知点E关于y轴的对称点坐标为（﹣ ，2），则图中阴影部分的面积是（   ） ‎ A. 1                                           B. 2                                           C. 3                                           D. 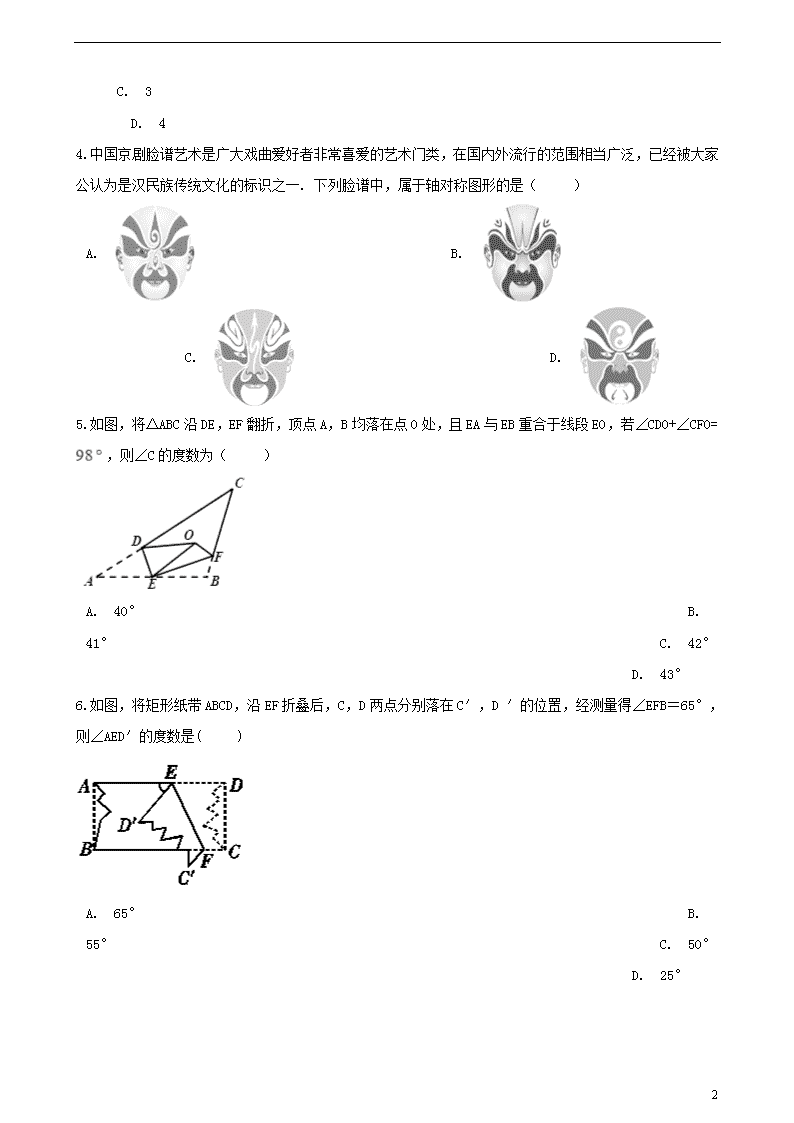4‎ ‎4.中国京剧脸谱艺术是广大戏曲爱好者非常喜爱的艺术门类，在国内外流行的范围相当广泛，已经被大家公认为是汉民族传统文化的标识之一. 下列脸谱中，属于轴对称图形的是（   ） ‎ A.                   B.                   C.                   D. ‎ ‎5.如图，将△ABC沿DE，EF翻折，顶点A，B均落在点O处，且EA与EB重合于线段EO，若∠CDO+∠CFO= ，则∠C的度数为（   ） ‎ 21‎ A. 40°                                       B. 41°                                       C. 42°                                       D. 43°‎ ‎6.如图，将矩形纸带ABCD，沿EF折叠后，C，D两点分别落在C′，D ′的位置，经测量得∠EFB＝65°，则∠AED′的度数是(   )‎ A. 65°                                       B. 55°                                       C. 50°                                       D. 25°‎ ‎7.如图，将∠BAC沿DE向∠BAC内折叠，使AD与A′D重合，A′E与AE重合，若∠A=30°，则∠1+∠2=（   ） ‎ A. 50°                                   B. 60°                                   C. 45°                                   D. 以上都不对 ‎8.已知 ABC(AB0),则CF=3x,∴DF= =x. ∴tan ∠DCF= ‎ ‎【解析】【分析】折叠以后，BC=CF，根据,在Rt△CDF中，可设CD=2x(x>0),则CF=3x,由勾股定理求出DF，再根据正切函数的定义求出tan ∠DCF。‎ ‎25.【答案】解:∵四边形ABCD是长方形, ∴AD∥BC, ∴∠DEF=∠EFG=50°,∠DEG+∠EGF=180°, 由折叠的性质可知∠D'EF=∠DEF=50°, ∴∠DEG=50°+50°=100°, ∴∠EGF=180°-∠DEG=180°-100°=80°, ∵∠BGD'=∠EGF ∴∠BGD'=80° ‎ ‎【解析】【分析】根据矩形的性质及平行线的性质，可证得∠DEF=∠EFG=50°,∠DEG+∠EGF=180°，再根据折叠的性质可证∠D'EF=∠DEF，然后求出∠DEG、∠EGF的度数，然后根据对顶角相等，可得出结果。‎ ‎26.【答案】（1）证明:∵DO⊥AB，∴∠DOB＝90°， ∴∠ACB＝∠DOB＝90°, 又∵∠B＝∠B．∴△DOB∽△ACB   （2）解：∵AD 平分∠CAB，DC⊥AC,DO⊥AB, ∴DO＝DC, 在 Rt△ABC 中，AC＝6，BC＝,8，∴AB＝10, ∵△DOB∽△ACB, ∴DO∶BO∶BD＝AC∶BC∶AB＝3∶4∶5, 设BD＝x，则DO＝DC＝ x，BO＝ x, ∵CD＋BD＝8，∴ x＋x＝8，解得x＝,5，即：BD＝5   （3）解：∵点B 与点B′关于直线DO 对称，∴∠B＝∠OB′D， ‎ 21‎ BO＝B′O＝ x，BD＝B′D＝x, ∵∠B 为锐角，∴∠OB′D 也为锐角，∴∠AB′D 为钝角, ∴当△AB′D 是等腰三角形时，AB′＝DB′, ∵AB′＋B′O＋BO＝10， ∴x＋ x＋ x＝10，解得x＝ ，即BD＝ ， ∴当△AB′D 为等腰三角形时，BD＝ .  ‎ ‎【解析】【分析】（1）根据垂直的定义得出∠DOB＝90°，根据等量代换得出∠ACB＝∠DOB＝90°,又∠B＝∠B，根据两个角对应相等的两个三角形相似得出△DOB∽△ACB； （2）根据角平分线上的点到角两边的距离相等得出DO＝DC,在 Rt△ABC 中，根据勾股定理得出AB＝10,根据相似三角形对应边成比例得出DO∶BO∶BD＝AC∶BC∶AB＝3∶4∶5,设BD＝x，则DO＝DC＝ x，BO＝ x,根据线段的和差，由CD＋BD＝8，列出方程，求解即可得出答案； （3）根据轴对称的性质得出∠B＝∠OB′D，BO＝B′O＝ x，BD＝B′D＝x,，根据等腰三角形的角来判定当△AB′D 是等腰三角形时，AB′＝DB′,由AB′＋B′O＋BO＝10，列出关于x的方程，求解得出x的值，从而得出答案。‎ 21‎