衡阳市2016年中考数学卷 21页

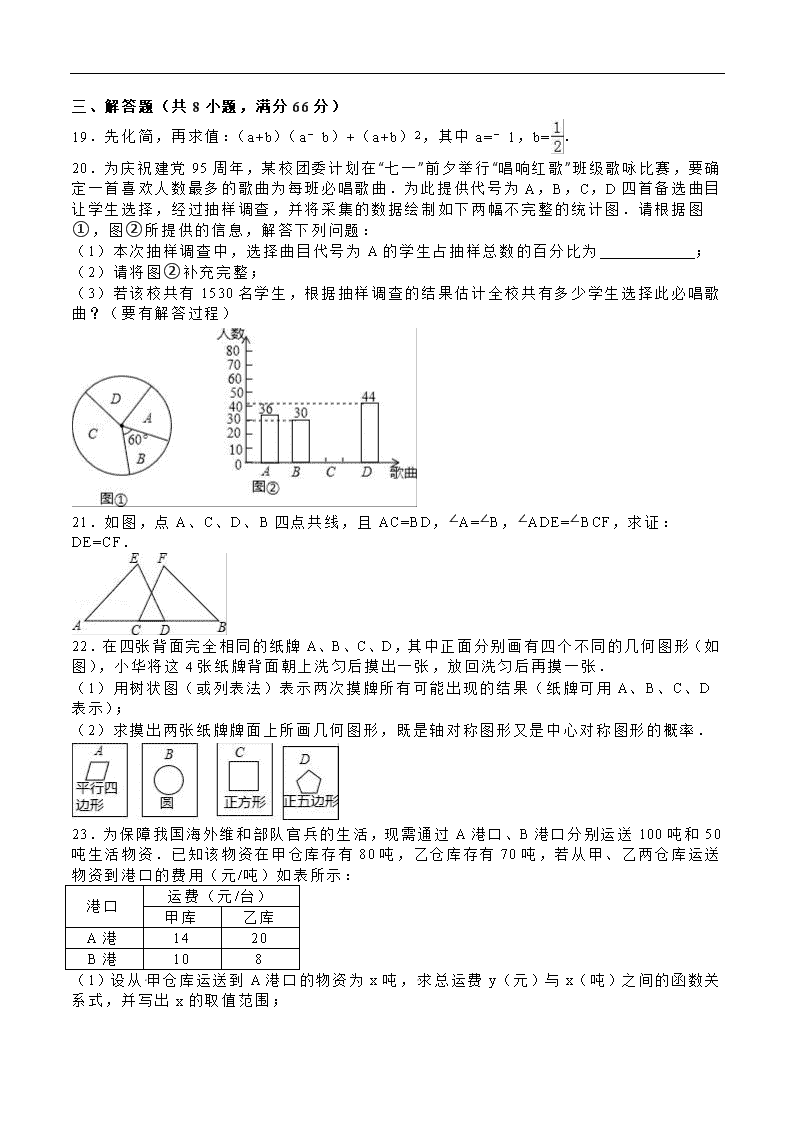
‎2016年湖南省衡阳市中考数学试卷 ‎　‎ 一、选择题（共12小题，每小题3分，满分36分）‎ ‎1．﹣4的相反数是（　　）‎ A．﹣B． C．﹣4 D．4‎ ‎2．如果分式有意义，则x的取值范围是（　　）‎ A．全体实数 B．x≠1 C．x=1 D．x＞1‎ ‎3．如图，直线AB∥CD，∠B=50°，∠C=40°，则∠E等于（　　）‎ A．70° B．80° C．90° D．100°‎ ‎4．下列几何体中，哪一个几何体的三视图完全相同（　　）‎ A．‎ 球体 B．‎ 圆柱体 C．‎ 四棱锥 D．‎ 圆锥 ‎5．下列各式中，计算正确的是（　　）‎ A．3x+5y=8xy B．x3•x5=x8C．x6÷x3=x2D．（﹣x3）3=x6‎ ‎6．为缓解中低收入人群和新参加工作的大学生住房的需求，某市将新建保障住房3600000套，把3600000用科学记数法表示应是（　　）‎ A．0.36×107B．3.6×106C．3.6×107D．36×105‎ ‎7．要判断一个学生的数学考试成绩是否稳定，那么需要知道他最近连续几次数学考试成绩的（　　）‎ A．平均数 B．中位数 C．众数 D．方差 ‎8．正多边形的一个内角是150°，则这个正多边形的边数为（　　）‎ A．10 B．11 C．12 D．13‎ ‎9．随着居民经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，抽样调查显示，截止2015年底某市汽车拥有量为16.9万辆．己知2013年底该市汽车拥有量为10万辆，设2013年底至2015年底该市汽车拥有量的平均增长率为x，根据题意列方程得（　　）‎ A．10（1+x）2=16.9 B．10（1+2x）=16.9 C．10（1﹣x）2=16.9 D．10（1﹣2x）=16.9‎ ‎10．关于x的一元二次方程x2+4x+k=0有两个相等的实根，则k的值为（　　）‎ A．k=﹣4 B．k=4 C．k≥﹣4 D．k≥4‎ ‎11．下列命题是假命题的是（　　）‎ A．经过两点有且只有一条直线 B．三角形的中位线平行且等于第三边的一半 C．平行四边形的对角线相等 D．圆的切线垂直于经过切点的半径 ‎12．如图，已知A，B是反比例函数y=（k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于x的函数图象大致为（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（共6小题，每小题3分，满分18分）‎ ‎13．因式分解：a2+ab=　　　　　　．‎ ‎14．计算：﹣=　　　　　　．‎ ‎15．点P（x﹣2，x+3）在第一象限，则x的取值范围是　　　　　　．‎ ‎16．若△ABC与△DEF相似且面积之比为25：16，则△ABC与△DEF的周长之比为　　　　　　．‎ ‎17．若圆锥底面圆的周长为8π，侧面展开图的圆心角为90°，则该圆锥的母线长为　　　　　　．‎ ‎18．如图所示，1条直线将平面分成2个部分，2条直线最多可将平面分成4个部分，3条直线最多可将平面分成7个部分，4条直线最多可将平面分成11个部分．现有n条直线最多可将平面分成56个部分，则n的值为　　　　　　．‎ ‎　‎ 三、解答题（共8小题，满分66分）‎ ‎19．先化简，再求值：（a+b）（a﹣b）+（a+b）2，其中a=﹣1，b=．‎ ‎20．为庆祝建党95周年，某校团委计划在“七一”前夕举行“唱响红歌”班级歌咏比赛，要确定一首喜欢人数最多的歌曲为每班必唱歌曲．为此提供代号为A，B，C，D四首备选曲目让学生选择，经过抽样调查，并将采集的数据绘制如下两幅不完整的统计图．请根据图①，图②所提供的信息，解答下列问题：‎ ‎（1）本次抽样调查中，选择曲目代号为A的学生占抽样总数的百分比为　　　　　　；‎ ‎（2）请将图②补充完整；‎ ‎（3）若该校共有1530名学生，根据抽样调查的结果估计全校共有多少学生选择此必唱歌曲？（要有解答过程）‎ ‎21．如图，点A、C、D、B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF，求证：DE=CF．‎ ‎22．在四张背面完全相同的纸牌A、B、C、D，其中正面分别画有四个不同的几何图形（如图），小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸一张．‎ ‎（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌可用A、B、C、D表示）；‎ ‎（2）求摸出两张纸牌牌面上所画几何图形，既是轴对称图形又是中心对称图形的概率．‎ ‎23．为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：‎ 港口 运费（元/台）‎ 甲库 乙库 A港 ‎14‎ ‎20‎ B港 ‎10‎ ‎8‎ ‎（1）设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；‎ ‎（2）求出最低费用，并说明费用最低时的调配方案．‎ ‎24．在某次海上军事学习期间，我军为确保△OBC海域内的安全，特派遣三艘军舰分别在O、B、C处监控△OBC海域，在雷达显示图上，军舰B在军舰O的正东方向80海里处，军舰C在军舰B的正北方向60海里处，三艘军舰上装载有相同的探测雷达，雷达的有效探测范围是半径为r的圆形区域．（只考虑在海平面上的探测）‎ ‎（1）若三艘军舰要对△OBC海域进行无盲点监控，则雷达的有效探测半径r至少为多少海里？‎ ‎（2）现有一艘敌舰A从东部接近△OBC海域，在某一时刻军舰B测得A位于北偏东60°方向上，同时军舰C测得A位于南偏东30°方向上，求此时敌舰A离△OBC海域的最短距离为多少海里？‎ ‎（3）若敌舰A沿最短距离的路线以20海里/小时的速度靠近△OBC海域，我军军舰B沿北偏东15°的方向行进拦截，问B军舰速度至少为多少才能在此方向上拦截到敌舰A？‎ ‎25．在平面直角坐标中，△ABC三个顶点坐标为A（﹣，0）、B（，0）、C（0，3）．‎ ‎（1）求△ABC内切圆⊙D的半径．‎ ‎（2）过点E（0，﹣1）的直线与⊙D相切于点F（点F在第一象限），求直线EF的解析式．‎ ‎（3）以（2）为条件，P为直线EF上一点，以P为圆心，以2为半径作⊙P．若⊙P上存在一点到△ABC三个顶点的距离相等，求此时圆心P的坐标．‎ ‎26．如图，抛物线y=ax2+bx+c经过△ABC的三个顶点，与y轴相交于（0，），点A坐标为（﹣1，2），点B是点A关于y轴的对称点，点C在x轴的正半轴上．‎ ‎（1）求该抛物线的函数关系表达式．‎ ‎（2）点F为线段AC上一动点，过F作FE⊥x轴，FG⊥y轴，垂足分别为E、G，当四边形OEFG为正方形时，求出F点的坐标．‎ ‎（3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在请说明理由．‎ ‎　‎ ‎2016年湖南省衡阳市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（共12小题，每小题3分，满分36分）‎ ‎1．﹣4的相反数是（　　）‎ A．﹣B． C．﹣4 D．4‎ ‎【考点】相反数．‎ ‎【分析】直接利用相反数的概念：只有符号不同的两个数叫做互为相反数，进而得出答案．‎ ‎【解答】解：﹣4的相反数是：4．‎ 故选：D．‎ ‎　‎ ‎2．如果分式有意义，则x的取值范围是（　　）‎ A．全体实数 B．x≠1 C．x=1 D．x＞1‎ ‎【考点】分式有意义的条件．‎ ‎【分析】直接利用分式有意义的条件得出x的值．‎ ‎【解答】解：∵分式有意义，‎ ‎∴x﹣1≠0，‎ 解得：x≠1．‎ 故选：B．‎ ‎　‎ ‎3．如图，直线AB∥CD，∠B=50°，∠C=40°，则∠E等于（　　）‎ A．70° B．80° C．90° D．100°‎ ‎【考点】平行线的性质．‎ ‎【分析】根据平行线的性质得到∠1=∠B=50°，由三角形的内角和即可得到结论．‎ ‎【解答】解：∵AB∥CD，‎ ‎∴∠1=∠B=50°，‎ ‎∵∠C=40°，‎ ‎∴∠E=180°﹣∠B﹣∠1=90°，‎ 故选C．‎ ‎　‎ ‎4．下列几何体中，哪一个几何体的三视图完全相同（　　）‎ A．‎ 球体 B．‎ 圆柱体 C．‎ 四棱锥 D．‎ 圆锥 ‎【考点】简单几何体的三视图．‎ ‎【分析】根据各个几何体的三视图的图形易求解．‎ ‎【解答】解：A、球体的三视图都是圆，故此选项正确；‎ B、圆柱的主视图和俯视图都是矩形，但左视图是一个圆形，故此选项错误；‎ C、四棱柱的主视图和左视图是一个三角形，俯视图是一个四边形，故此选项错误；‎ D、圆锥的主视图和左视图是相同的，都为一个三角形，但是俯视图是一个圆形，故此选项错误．‎ 故选：A．‎ ‎　‎ ‎5．下列各式中，计算正确的是（　　）‎ A．3x+5y=8xy B．x3•x5=x8C．x6÷x3=x2D．（﹣x3）3=x6‎ ‎【考点】同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．‎ ‎【分析】分别利用同底数幂的乘除法运算法则以及合并同类项法则、积的乘方运算法则分别计算得出答案．‎ ‎【解答】解：A、3x+5y，无法计算，故此选项错误；‎ B、x3•x5=x8，故此选项正确；‎ C、x6÷x3=x3，故此选项错误；‎ D、（﹣x3）3=﹣x9，故此选项错误；‎ 故选：B．‎ ‎　‎ ‎6．为缓解中低收入人群和新参加工作的大学生住房的需求，某市将新建保障住房3600000套，把3600000用科学记数法表示应是（　　）‎ A．0.36×107B．3.6×106C．3.6×107D．36×105‎ ‎【考点】科学记数法—表示较大的数．‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．‎ ‎【解答】解：3600000=3.6×106，‎ 故选：B．‎ ‎　‎ ‎7．要判断一个学生的数学考试成绩是否稳定，那么需要知道他最近连续几次数学考试成绩的（　　）‎ A．平均数 B．中位数 C．众数 D．方差 ‎【考点】统计量的选择．‎ ‎【分析】根据方差的意义：方差是反映一组数据波动大小，稳定程度的量；方差越大，表明这组数据偏离平均数越大，即波动越大，反之也成立．标准差是方差的平方根，也能反映数据的波动性；故要判断他的数学成绩是否稳定，那么需要知道他最近连续几次数学考试成绩的方差．‎ ‎【解答】解：方差是衡量波动大小的量，方差越小则波动越小，稳定性也越好．‎ 故选：D ‎　‎ ‎8．正多边形的一个内角是150°，则这个正多边形的边数为（　　）‎ A．10 B．11 C．12 D．13‎ ‎【考点】多边形内角与外角．‎ ‎【分析】一个正多边形的每个内角都相等，根据内角与外角互为邻补角，因而就可以求出外角的度数．根据任何多边形的外角和都是360度，利用360除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．‎ ‎【解答】解：外角是：180°﹣150°=30°，‎ ‎360°÷30°=12．‎ 则这个正多边形是正十二边形．‎ 故选：C．‎ ‎　‎ ‎9．随着居民经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，抽样调查显示，截止2015年底某市汽车拥有量为16.9万辆．己知2013年底该市汽车拥有量为10万辆，设2013年底至2015年底该市汽车拥有量的平均增长率为x，根据题意列方程得（　　）‎ A．10（1+x）2=16.9 B．10（1+2x）=16.9 C．10（1﹣x）2=16.9 D．10（1﹣2x）=16.9‎ ‎【考点】由实际问题抽象出一元二次方程．‎ ‎【分析】根据题意可得：2013年底该市汽车拥有量×（1+增长率）2=2015年底某市汽车拥有量，根据等量关系列出方程即可．‎ ‎【解答】解：设2013年底至2015年底该市汽车拥有量的平均增长率为x，‎ 根据题意，可列方程：10（1+x）2=16.9，‎ 故选：A．‎ ‎　‎ ‎10．关于x的一元二次方程x2+4x+k=0有两个相等的实根，则k的值为（　　）‎ A．k=﹣4 B．k=4 C．k≥﹣4 D．k≥4‎ ‎【考点】根的判别式．‎ ‎【分析】根据判别式的意义得到△=42﹣4k=0，然后解一次方程即可．‎ ‎【解答】解：∵一元二次方程x2+4x+k=0有两个相等的实根，‎ ‎∴△=42﹣4k=0，‎ 解得：k=4，‎ 故选：B．‎ ‎　‎ ‎11．下列命题是假命题的是（　　）‎ A．经过两点有且只有一条直线 B．三角形的中位线平行且等于第三边的一半 C．平行四边形的对角线相等 D．圆的切线垂直于经过切点的半径 ‎【考点】命题与定理．‎ ‎【分析】根据直线公理、三角形中位线定理、切线性质定理即可判断A、B、D正确．‎ ‎【解答】解：A、经过两点有且只有一条直线，正确．‎ B、三角形的中位线平行且等于第三边的一半，正确．‎ C、平行四边形的对角线相等，错误．矩形的对角线相等，平行四边形的对角线不一定相等．‎ D、圆的切线垂直于经过切点的半径，正确．‎ 故选C．‎ ‎　‎ ‎12．如图，已知A，B是反比例函数y=（k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于x的函数图象大致为（　　）‎ A． B． C． D．‎ ‎【考点】动点问题的函数图象．‎ ‎【分析】结合点P的运动，将点P的运动路线分成O→A、A→B、B→C三段位置来进行分析三角形OMP面积的计算方式，通过图形的特点分析出面积变化的趋势，从而得到答案．‎ ‎【解答】解：设∠AOM=α，点P运动的速度为a，‎ 当点P从点O运动到点A的过程中，S==a2•cosα•sinα•t2，‎ 由于α及a均为常量，从而可知图象本段应为抛物线，且S随着t的增大而增大；‎ 当点P从A运动到B时，由反比例函数性质可知△OPM的面积为k，保持不变，‎ 故本段图象应为与横轴平行的线段；‎ 当点P从B运动到C过程中，OM的长在减少，△OPM的高与在B点时相同，‎ 故本段图象应该为一段下降的线段；‎ 故选：A．‎ ‎　‎ 二、填空题（共6小题，每小题3分，满分18分）‎ ‎13．因式分解：a2+ab=　a（a+b）　．‎ ‎【考点】因式分解-提公因式法．‎ ‎【分析】直接把公因式a提出来即可．‎ ‎【解答】解：a2+ab=a（a+b）．‎ 故答案为：a（a+b）．‎ ‎　‎ ‎14．计算：﹣=　1　．‎ ‎【考点】分式的加减法．‎ ‎【分析】由于两分式的分母相同，分子不同，故根据同分母的分式相加减的法则进行计算即可．‎ ‎【解答】解：原式=‎ ‎=1．‎ 故答案为：1．‎ ‎　‎ ‎15．点P（x﹣2，x+3）在第一象限，则x的取值范围是　x＞2　．‎ ‎【考点】点的坐标．‎ ‎【分析】直接利用第一象限点的坐标特征得出x的取值范围即可．‎ ‎【解答】解：∵点P（x﹣2，x+3）在第一象限，‎ ‎∴，‎ 解得：x＞2．‎ 故答案为：x＞2．‎ ‎　‎ ‎16．若△ABC与△DEF相似且面积之比为25：16，则△ABC与△DEF的周长之比为　5：4　．‎ ‎【考点】相似三角形的性质．‎ ‎【分析】根据相似三角形面积的比等于相似比的平方求出相似比，再根据相似三角形周长的比等于相似比求解．‎ ‎【解答】解：∵△ABC与△DEF相似且面积之比为25：16，‎ ‎∴△ABC与△DEF的相似比为5：4；‎ ‎∴△ABC与△DEF的周长之比为5：4．‎ 故答案为：5：4．‎ ‎　‎ ‎17．若圆锥底面圆的周长为8π，侧面展开图的圆心角为90°，则该圆锥的母线长为　16　．‎ ‎【考点】圆锥的计算．‎ ‎【分析】设该圆锥的母线长为l，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到8π=，然后解方程即可．‎ ‎【解答】解：设该圆锥的母线长为l，‎ 根据题意得8π=，解得l=16，‎ 即该圆锥的母线长为16．‎ 故答案为16．‎ ‎　‎ ‎18．如图所示，1条直线将平面分成2个部分，2条直线最多可将平面分成4个部分，3条直线最多可将平面分成7个部分，4条直线最多可将平面分成11个部分．现有n条直线最多可将平面分成56个部分，则n的值为　10　．‎ ‎【考点】点、线、面、体．‎ ‎【分析】n条直线最多可将平面分成S=1+1+2+3…+n=n（n+1）+1，依此可得等量关系：n条直线最多可将平面分成56个部分，列出方程求解即可．‎ ‎【解答】解：依题意有 n（n+1）+1=56，‎ 解得x1=﹣11（不合题意舍去），x2=10．‎ 答：n的值为10．‎ 故答案为：10．‎ ‎　‎ 三、解答题（共8小题，满分66分）‎ ‎19．先化简，再求值：（a+b）（a﹣b）+（a+b）2，其中a=﹣1，b=．‎ ‎【考点】整式的混合运算—化简求值．‎ ‎【分析】原式利用平方差公式、完全平方公式展开后再合并同类项即可化简，将a、b的值代入求值即可．‎ ‎【解答】解：原式=a2﹣b2+a2+2ab+b2‎ ‎=2a2+2ab，‎ 当a=﹣1，b=时，‎ 原式=2×（﹣1）2+2×（﹣1）×‎ ‎=2﹣1‎ ‎=1．‎ ‎　‎ ‎20．为庆祝建党95周年，某校团委计划在“七一”前夕举行“唱响红歌”班级歌咏比赛，要确定一首喜欢人数最多的歌曲为每班必唱歌曲．为此提供代号为A，B，C，D四首备选曲目让学生选择，经过抽样调查，并将采集的数据绘制如下两幅不完整的统计图．请根据图①，图②所提供的信息，解答下列问题：‎ ‎（1）本次抽样调查中，选择曲目代号为A的学生占抽样总数的百分比为　20%　；‎ ‎（2）请将图②补充完整；‎ ‎（3）若该校共有1530名学生，根据抽样调查的结果估计全校共有多少学生选择此必唱歌曲？（要有解答过程）‎ ‎【考点】条形统计图；用样本估计总体；扇形统计图．‎ ‎【分析】（1）根据条形统计图和扇形统计图可以求得选择曲目代号为A的学生占抽样总数的百分比；‎ ‎（2）根据条形统计图和扇形统计图可以求得选择C的人数，从而可以将图②补充完整；‎ ‎（3）根据条形统计图和扇形统计图可以估计全校选择此必唱歌曲的人数．‎ ‎【解答】解：（1）由题意可得，‎ 本次抽样调查中，选择曲目代号为A的学生占抽样总数的百分比为：×100%=20%．‎ 故答案为：20%；‎ ‎（2）由题意可得，‎ 选择C的人数有：30÷﹣36﹣30﹣44=70（人），‎ 故补全的图②如下图所示，‎ ‎（3）由题意可得，‎ 全校选择此必唱歌曲共有：1530×=595（人），‎ 即全校共有595名学生选择此必唱歌曲．‎ ‎　‎ ‎21．如图，点A、C、D、B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF，求证：DE=CF．‎ ‎【考点】全等三角形的判定与性质．‎ ‎【分析】求出AD=BC，根据ASA推出△AED≌△BFC，根据全等三角形的性质得出即可．‎ ‎【解答】证明：∵AC=BD，‎ ‎∴AC+CD=BD+CD，‎ ‎∴AD=BC，‎ 在△AED和△BFC中，‎ ‎，‎ ‎∴△AED≌△BFC（ASA），‎ ‎∴DE=CF．‎ ‎　‎ ‎22．在四张背面完全相同的纸牌A、B、C、D，其中正面分别画有四个不同的几何图形（如图），小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸一张．‎ ‎（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌可用A、B、C、D表示）；‎ ‎（2）求摸出两张纸牌牌面上所画几何图形，既是轴对称图形又是中心对称图形的概率．‎ ‎【考点】列表法与树状图法．‎ ‎【分析】（1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果；‎ ‎（2）由既是轴对称图形又是中心对称图形的有4种情况，直接利用概率公式求解即可求得答案．‎ ‎【解答】解（1）画树状图得：‎ 则共有16种等可能的结果；‎ ‎（2）∵既是中心对称又是轴对称图形的只有B、C，‎ ‎∴既是轴对称图形又是中心对称图形的有4种情况，‎ ‎∴既是轴对称图形又是中心对称图形的概率为： =．‎ ‎　‎ ‎23．为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：‎ 港口 运费（元/台）‎ 甲库 乙库 A港 ‎14‎ ‎20‎ B港 ‎10‎ ‎8‎ ‎（1）设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；‎ ‎（2）求出最低费用，并说明费用最低时的调配方案．‎ ‎【考点】一次函数的应用．‎ ‎【分析】（1）根据题意表示出甲仓库和乙仓库分别运往A、B两港口的物资数，再由等量关系：总运费=甲仓库运往A港口的费用+甲仓库运往B港口的费用+乙仓库运往A港口的费用+乙仓库运往B港口的费用列式并化简；最后根据不等式组得出x的取值；‎ ‎（2）因为所得的函数为一次函数，由增减性可知：y随x增大而减少，则当x=80时，y最小，并求出最小值，写出运输方案．‎ ‎【解答】解（1）设从甲仓库运x吨往A港口，则从甲仓库运往B港口的有（80﹣x）吨，‎ 从乙仓库运往A港口的有吨，运往B港口的有50﹣（80﹣x）=（x﹣30）吨，‎ 所以y=14x+20+10（80﹣x）+8（x﹣30）=﹣8x+2560，‎ x的取值范围是30≤x≤80．‎ ‎（2）由（1）得y=﹣8x+2560y随x增大而减少，所以当x=80时总运费最小，‎ 当x=80时，y=﹣8×80+2560=1920，‎ 此时方案为：把甲仓库的全部运往A港口，再从乙仓库运20吨往A港口，乙仓库的余下的全部运往B港口．‎ ‎　‎ ‎24．在某次海上军事学习期间，我军为确保△OBC海域内的安全，特派遣三艘军舰分别在O、B、C处监控△OBC海域，在雷达显示图上，军舰B在军舰O的正东方向80海里处，军舰C在军舰B的正北方向60海里处，三艘军舰上装载有相同的探测雷达，雷达的有效探测范围是半径为r的圆形区域．（只考虑在海平面上的探测）‎ ‎（1）若三艘军舰要对△OBC海域进行无盲点监控，则雷达的有效探测半径r至少为多少海里？‎ ‎（2）现有一艘敌舰A从东部接近△OBC海域，在某一时刻军舰B测得A位于北偏东60°方向上，同时军舰C测得A位于南偏东30°方向上，求此时敌舰A离△OBC海域的最短距离为多少海里？‎ ‎（3）若敌舰A沿最短距离的路线以20海里/小时的速度靠近△OBC海域，我军军舰B沿北偏东15°的方向行进拦截，问B军舰速度至少为多少才能在此方向上拦截到敌舰A？‎ ‎【考点】解直角三角形的应用-方向角问题．‎ ‎【分析】（1）求出OC，由题意r≥OC，由此即可解决问题．‎ ‎（2）作AM⊥BC于M，求出AM即可解决问题．‎ ‎（3）假设B军舰在点N处拦截到敌舰．在BM上取一点H，使得HB=HN，设MN=x，先列出方程求出x，再求出BN、AN利用不等式解决问题．‎ ‎【解答】解：（1）在RT△OBC中，∵BO=80，BC=60，∠OBC=90°，‎ ‎∴OC===100，‎ ‎∵OC=×100=50‎ ‎∴雷达的有效探测半径r至少为50海里．‎ ‎（2）作AM⊥BC于M，‎ ‎∵∠ACB=30°，∠CBA=60°，‎ ‎∴∠CAB=90°，‎ ‎∴AB=BC=30，‎ 在RT△ABM中，∵∠AMB=90°，AB=30，∠BAM=30°，‎ ‎∴BM=AB=15，AM=BM=15，‎ ‎∴此时敌舰A离△OBC海域的最短距离为15海里．‎ ‎（3）假设B军舰在点N处拦截到敌舰．在BM上取一点H，使得HB=HN，设MN=x，‎ ‎∵∠HBN=∠HNB=15°，‎ ‎∴∠MHN=∠HBN+∠HNB=30°，‎ ‎∴HN=HB=2x，MH=x，‎ ‎∵BM=15，‎ ‎∴15=x+2x，‎ x=30﹣15，‎ ‎∴AN=30﹣30，‎ BN==15（﹣），设B军舰速度为a海里/小时，‎ 由题意≤，‎ ‎∴a≥20．‎ ‎∴B军舰速度至少为20海里/小时．‎ ‎　‎ ‎25．在平面直角坐标中，△ABC三个顶点坐标为A（﹣，0）、B（，0）、C（0，3）．‎ ‎（1）求△ABC内切圆⊙D的半径．‎ ‎（2）过点E（0，﹣1）的直线与⊙D相切于点F（点F在第一象限），求直线EF的解析式．‎ ‎（3）以（2）为条件，P为直线EF上一点，以P为圆心，以2为半径作⊙P．若⊙P上存在一点到△ABC三个顶点的距离相等，求此时圆心P的坐标．‎ ‎【考点】圆的综合题．‎ ‎【分析】（1）由A、B、C三点坐标可知∠CBO=60°，又因为点D是△ABC的内心，所以BD平分∠CBO，然后利用锐角三角函数即可求出OD的长度；‎ ‎（2）根据题意可知，DF为半径，且∠DFE=90°，过点F作FG⊥y轴于点G，求得FG和OG的长度，即可求出点F的坐标，然后将E和F的坐标代入一次函数解析式中，即可求出直线EF的解析式；‎ ‎（3）⊙P上存在一点到△ABC三个顶点的距离相等，该点是△ABC的外接圆圆心，即为点D，所以DP=2，又因为点P在直线EF上，所以这样的点P共有2个，且由勾股定理可知PF=3．‎ ‎【解答】解：（1）连接BD，‎ ‎∵B（，0），C（0，3），‎ ‎∴OB=，OC=3，‎ ‎∴tan∠CBO==，‎ ‎∴∠CBO=60°‎ ‎∵点D是△ABC的内心，‎ ‎∴BD平分∠CBO，‎ ‎∴∠DBO=30°，‎ ‎∴tan∠DBO=，‎ ‎∴OD=1，‎ ‎∴△ABC内切圆⊙D的半径为1；‎ ‎（2）连接DF，‎ 过点F作FG⊥y轴于点G，‎ ‎∵E（0，﹣1）‎ ‎∴OE=1，DE=2，‎ ‎∵直线EF与⊙D相切，‎ ‎∴∠DFE=90°，DF=1，‎ ‎∴sin∠DEF=，‎ ‎∴∠DEF=30°，‎ ‎∴∠GDF=60°，‎ ‎∴在Rt△DGF中，‎ ‎∠DFG=30°，‎ ‎∴DG=，‎ 由勾股定理可求得：GF=，‎ ‎∴F（，），‎ 设直线EF的解析式为：y=kx+b，‎ ‎∴，‎ ‎∴直线EF的解析式为：y=x﹣1；‎ ‎（3）∵⊙P上存在一点到△ABC三个顶点的距离相等，‎ ‎∴该点必为△ABC外接圆的圆心，‎ 由（1）可知：△ABC是等边三角形，‎ ‎∴△ABC外接圆的圆心为点D ‎∴DP=2，‎ 设直线EF与x轴交于点H，‎ ‎∴令y=0代入y=x﹣1，‎ ‎∴x=，‎ ‎∴H（，0），‎ ‎∴FH=，‎ 当P在x轴上方时，‎ 过点P1作P1M⊥x轴于M，‎ 由勾股定理可求得：P1F=3，‎ ‎∴P1H=P1F+FH=，‎ ‎∵∠DEF=∠HP1M=30°，‎ ‎∴HM=P1H=，P1M=5，‎ ‎∴OM=2，‎ ‎∴P1（2，5），‎ 当P在x轴下方时，‎ 过点P2作P2N⊥x轴于点N，‎ 由勾股定理可求得：P2F=3，‎ ‎∴P2H=P2F﹣FH=，‎ ‎∴∠DEF=30°‎ ‎∴∠OHE=60°‎ ‎∴sin∠OHE=，‎ ‎∴P2N=4，‎ 令y=﹣4代入y=x﹣1，‎ ‎∴x=﹣，‎ ‎∴P2（﹣，﹣4），‎ 综上所述，若⊙P上存在一点到△ABC三个顶点的距离相等，此时圆心P的坐标为（2，5）或（﹣，﹣4）．‎ ‎　‎ ‎26．如图，抛物线y=ax2+bx+c经过△ABC的三个顶点，与y轴相交于（0，），点A坐标为（﹣1，2），点B是点A关于y轴的对称点，点C在x轴的正半轴上．‎ ‎（1）求该抛物线的函数关系表达式．‎ ‎（2）点F为线段AC上一动点，过F作FE⊥x轴，FG⊥y轴，垂足分别为E、G，当四边形OEFG为正方形时，求出F点的坐标．‎ ‎（3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在请说明理由．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）易得抛物线的顶点为（0，），然后只需运用待定系数法，就可求出抛物线的函数关系表达式；‎ ‎（2）①当点F在第一象限时，如图1，可求出点C的坐标，直线AC的解析式，设正方形OEFG的边长为p，则F（p，p），代入直线AC的解析式，就可求出点F的坐标；②当点F在第二象限时，同理可求出点F的坐标，此时点F不在线段AC上，故舍去；‎ ‎（3）过点M作MH⊥DN于H，如图2，由题可得0≤t≤2．然后只需用t的式子表示DN、DM2、MN2，分三种情况（①DN=DM，②ND=NM，③MN=MD）讨论就可解决问题．‎ ‎【解答】解：（1）∵点B是点A关于y轴的对称点，‎ ‎∴抛物线的对称轴为y轴，‎ ‎∴抛物线的顶点为（0，），‎ 故抛物线的解析式可设为y=ax2+．‎ ‎∵A（﹣1，2）在抛物线y=ax2+上，‎ ‎∴a+=2，‎ 解得a=﹣，‎ ‎∴抛物线的函数关系表达式为y=﹣x2+；‎ ‎（2）①当点F在第一象限时，如图1，‎ 令y=0得，﹣x2+=0，‎ 解得：x1=3，x2=﹣3，‎ ‎∴点C的坐标为（3，0）．‎ 设直线AC的解析式为y=mx+n，‎ 则有，‎ 解得，‎ ‎∴直线AC的解析式为y=﹣x+．‎ 设正方形OEFG的边长为p，则F（p，p）．‎ ‎∵点F（p，p）在直线y=﹣x+上，‎ ‎∴﹣p+=p，‎ 解得p=1，‎ ‎∴点F的坐标为（1，1）．‎ ‎②当点F在第二象限时，‎ 同理可得：点F的坐标为（﹣3，3），‎ 此时点F不在线段AC上，故舍去．‎ 综上所述：点F的坐标为（1，1）；‎ ‎（3）过点M作MH⊥DN于H，如图2，‎ 则OD=t，OE=t+1．‎ ‎∵点E和点C重合时停止运动，∴0≤t≤2．‎ 当x=t时，y=﹣t+，则N（t，﹣t+），DN=﹣t+．‎ 当x=t+1时，y=﹣（t+1）+=﹣t+1，则M（t+1，﹣t+1），ME=﹣t+1．‎ 在Rt△DEM中，DM2=12+（﹣t+1）2=t2﹣t+2．‎ 在Rt△NHM中，MH=1，NH=（﹣t+）﹣（﹣t+1）=，‎ ‎∴MN2=12+（）2=．‎ ‎①当DN=DM时，‎ ‎（﹣t+）2=t2﹣t+2，‎ 解得t=；‎ ‎②当ND=NM时，‎ ‎﹣t+==，‎ 解得t=3﹣；‎ ‎③当MN=MD时，‎ ‎=t2﹣t+2，‎ 解得t1=1，t2=3．‎ ‎∵0≤t≤2，∴t=1．‎ 综上所述：当△DMN是等腰三角形时，t的值为，3﹣或1．‎ ‎　‎