2008年常州市数学中考试卷 8页

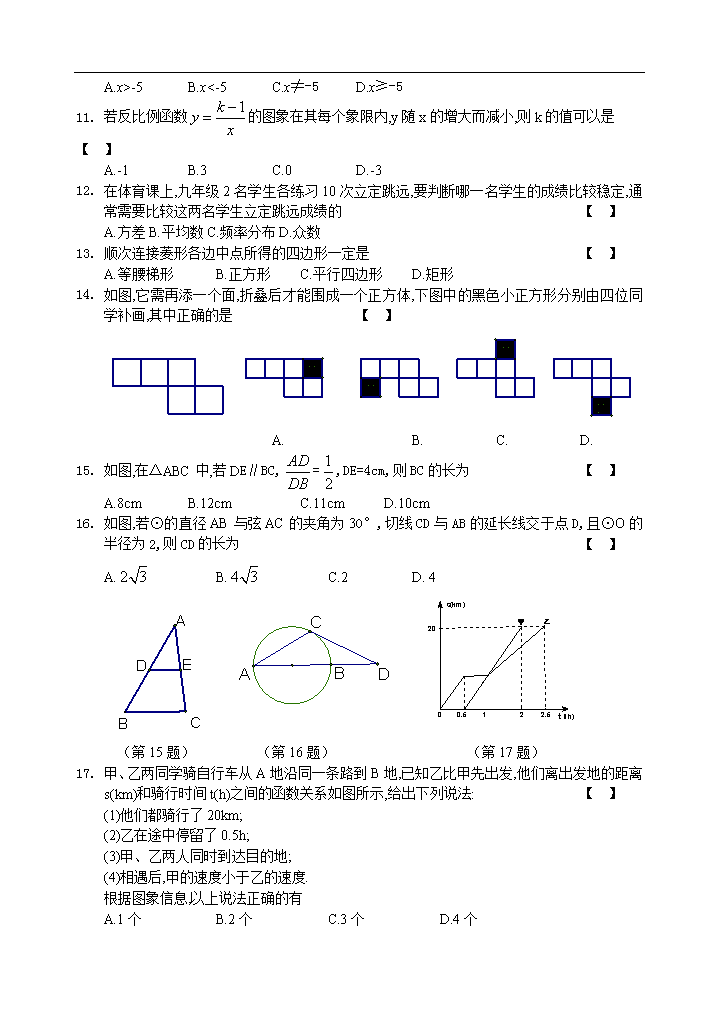
总 分 核分人 结分人 核分人 常州市二二〇〇八年初中毕业、升学统一考试 数 学 试 卷 注意事项：1.全卷共8页，28题，满分120分，考试时间120分钟.‎ ‎2.用蓝色或黑色钢笔、圆珠笔直接答在试卷上.‎ ‎3.答卷前将密封线内的项目填写清楚,并将座位号填写在试卷规定的位置上.‎ ‎4.考生在答题过程中,不得使用任何型号的计算器,若试题计算结果没有要求取近似值,则计算结果取精确值(保留根号和π).‎ 得分 评卷人 一.填空题(本大题每个空格1分,共18分,把答案填在题中横线上)‎ 1. ‎-3的相反数是_______,-的绝对值是________,2-1=______.‎ 2. 点A(-2,1)关于y轴对称的点的坐标为___________,关于原点对称的点的坐标为________.‎ 3. 如图,在△ABC中BE平分∠ABC,DE∥BC,∠ABE=35°,则∠DEB=______°,∠ADE=_______°. ‎ 4. 已知一组数据为5,6,8,6,8,8,8,则这组数据的众数是_________,平均数是_________.‎ 5. 已知扇形的半径为‎3cm,扇形的弧长为πcm,则该扇形的面积是______cm2,扇形的圆心角为______°.‎ ‎_‎ ‎4‎ 6. 过反比例函数的图象上的一点分别作x、y轴的垂线段,如果垂线段与x、y轴所围成的矩形面积是6,那么该函数的表达式是______;若点A(-3,m)在这个反比例函数的图象上,则m=______.‎ 7. 已知函数的部分图象如图所示,则c=______,当x______时,y随x的增大而减小. ‎ 8. 若将棱长为2的正方体切成8个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍; 若将棱长为3的正方体切成27个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍; 若将棱长为n(n>1,且为整数)的正方体切成n3个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍.‎ 得分 评卷人 二.选择题(在每小题给出的四个选项中,只有一项最符合题目要求,把符合要求的选项的代号填在题后的【 】内,每小题2分,共18分)‎ 9. 下列实数中,无理数是 【 】‎ A. B. C. D. ‎ 10. 若式子在实数范围内有意义,则x的取值范围是 【 】‎ A.x>-5 B.x<‎-5 ‎ C.x≠-5 D.x≥-5 ‎ 1. 若反比例函数的图象在其每个象限内,y随x的增大而减小,则k的值可以是 ‎【 】‎ A.-1 B‎.3 ‎ C.0 D.-3‎ 2. 在体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生立定跳远成绩的 【 】‎ A.方差B.平均数C.频率分布D.众数 3. 顺次连接菱形各边中点所得的四边形一定是 【 】‎ A.等腰梯形 B.正方形 C.平行四边形 D.矩形 4. 如图,它需再添一个面,折叠后才能围成一个正方体,下图中的黑色小正方形分别由四位同学补画,其中正确的是 【 】‎ ‎ ‎ A. B. C. D.‎ 5. 如图,在△ABC中,若DE∥BC,=,DE=‎4cm,则BC的长为 【 】‎ A‎.8cm B‎.12cm C‎.11cm D‎.10cm ‎ 6. 如图,若⊙的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为 【 】‎ A. B. C.2 D. 4‎ ‎（第15题） （第16题） （第17题）‎ 7. 甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示,给出下列说法: 【 】‎ ‎(1)他们都骑行了‎20km;‎ ‎(2)乙在途中停留了0.5h;‎ ‎(3)甲、乙两人同时到达目的地;‎ ‎(4)相遇后,甲的速度小于乙的速度. ‎ 根据图象信息,以上说法正确的有 A.1个 B.2个 C.3个 D.4个 得分 评卷人 三.解答题(本大题共2小题,共18分,解答时应写出演算步骤)‎ 1. ‎(本小题满分10分)化简:‎ ‎(1) (2)‎ ‎ ‎ 2. 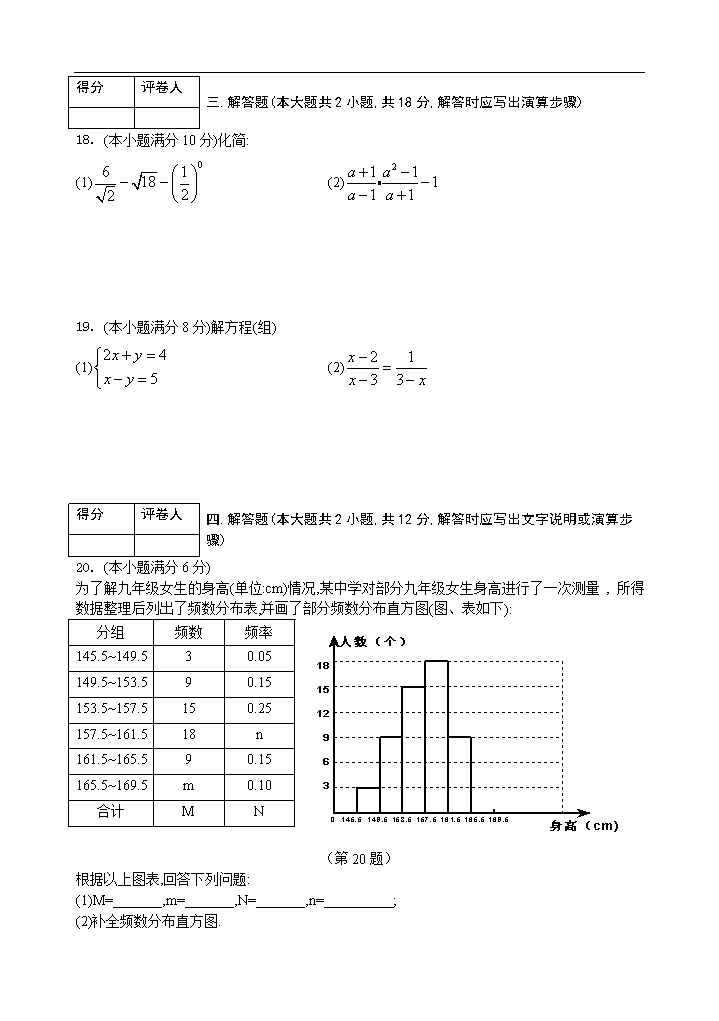‎(本小题满分8分)解方程(组)‎ ‎(1) (2)‎ ‎ ‎ 得分 评卷人 四.解答题(本大题共2小题,共12分,解答时应写出文字说明或演算步骤)‎ 3. ‎(本小题满分6分)‎ 为了解九年级女生的身高(单位:cm)情况,某中学对部分九年级女生身高进行了一次测量 , 所得数据整理后列出了频数分布表,并画了部分频数分布直方图(图、表如下):‎ 分组 频数 频率 ‎145.5~149.5‎ ‎3‎ ‎0.05‎ ‎149.5~153.5‎ ‎9‎ ‎0.15‎ ‎153.5~157.5‎ ‎15‎ ‎0.25‎ ‎157.5~161.5‎ ‎18‎ n ‎161.5~165.5‎ ‎9‎ ‎0.15‎ ‎165.5~169.5‎ m ‎0.10‎ 合计 M N ‎（第20题）‎ 根据以上图表,回答下列问题:‎ ‎(1)M=_______,m=_______,N=_______,n=__________;‎ ‎(2)补全频数分布直方图.‎ 1. ‎（本小题满分6分）‎ 小敏和小李都想去看我市举行的乒乓球比赛,但俩人只有一张门票.小敏建议通过摸球来决定谁去欣赏,他的方法是:把1个白球和2个红球放在一只不透明的袋子中(这些球除颜色外都相同,搅匀后从中任意摸出1个球,记录下颜色后放袋中并搅匀,再从中任意摸出1个球.如果两次都摸出相同颜色的球,则小敏自己去看比赛,否则小李去看比赛.问小敏的这个方法对双方公平吗?请说明理由.‎ 得分 评卷人 五.解答题(本大题共2小题,共14分,解答时应写出证明过程)‎ 2. ‎(本小题满分7分)‎ 已知:如图,AB=AD,AC=AE,∠BAD=∠CAE.‎ 求证:AC=DE. ‎ 1. 已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.‎ 求证:AE平分∠BAD.‎ 得分 评卷人 五.画图与探究(本大题共2小题,共14分)‎ 2. ‎(本小题满分6分)‎ 已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.‎ (1) 在所给网格中按下列要求画图:‎ ① 在网格中建立平面直角坐标系(坐标原点为O),使四边形ABCD各个顶点的坐标分别为A(-5,0)、B(-4,0)、C(-1,3),D(-5,1);‎ ② 将四边形ABCD沿坐标横轴翻折180°,得到四边形A’B’C’D’,再将四边形A’B’C’D’绕原点O旋转180°,得到四边形A”B”C”D”;‎ ‎(2)写出C”、D”的坐标;‎ ‎(3)请判断四边形A”B”C”D”与四边形ABCD成何种对称?若成中心对称,请写出对称中心;若成轴对称,请写出对称轴.‎ ‎(第24题)‎ 3. 如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长. ‎ 得分 评卷人 五.解答题(本大题共3小题,共26分,解答时应写出文字说明、证明过程或演算步骤)‎ 1. ‎(本小题满分8分)‎ 如图,港口B位于港口O正西方向120海里外,小岛C位于港口O北偏西60°的方向.一艘科学考察船从港口O出发,沿北偏西30°的OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给物资后,立即按原来的速度给考察船送去.‎ (1) 快艇从港口B到小岛C需要多少时间?‎ 北 ‎30°‎ ‎30°‎ 东 O B C A ‎（第26题）‎ 北 (2) 快艇从小岛C出发后最少需要多少时间才能和考察船相遇?‎ 北 2. ‎(本小题满分7分)‎ ‎2008年5月12日四川汶川地区发生8.0级特大地震.举国上下通过各种方式表达爱心.某企业决定用p万元援助灾区n所学校,用于搭建帐篷和添置教学设备.根据各校不同的受灾情况,该企业捐款的分配方案是:所有学校得到的捐款数都相等,到第n所学校的捐款恰好分完,捐款的分配方法如下表所示.(其中p,n,a都是正整数)‎ 分配顺序 分配数额(单位:万元)‎ 帐篷费用 教学设备费用 第1所学校 ‎5‎ 剩余款的 第2所学校 ‎10‎ 剩余款的 第3所学校 ‎15‎ 剩余款的 ‎…‎ ‎…‎ ‎…‎ 第（n-1）所学校 ‎5(n-1)‎ 剩余款的 第n所学校 ‎5n ‎0‎ 根据以上信息，解答下列问题：‎ ‎(1)写出p与n的关系式；‎ ‎(2)当p=125时，该企业能援助多少所学校？‎ ‎(3)根据震区灾情，该企业计划再次提供不超过‎20a万元的捐款,按照原来的分配方案援助其它学校.若a由 (2)确定,则再次提供的捐款最多又可以援助多少所学校?‎ 1. 如图,抛物线与x轴分别相交于点B、O,它的顶点为A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.‎ (1) 求点A的坐标;‎ (2) 以点A、B、O、P为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P的坐标;‎ (3) 设以点A、B、O、P为顶点的四边形的面积为S,点P的横坐标为x,当时,求x的取值范围. ‎