上海市闸北区中考数学二模试卷 5页

‎2016年上海市闸北区中考数学二模试卷 ‎　‎ 一．选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．（4分）下列代数式中，属于分式的是（　　）‎ A．﹣3 B． C． D．﹣4a3b ‎2．（4分）的值为（　　）‎ A．2 B．﹣2 C．土2 D．不存在 ‎3．（4分）下列方程中，没有实数根的方程是（　　）‎ A．x2+2x﹣1=0 B．x2+2x+1=0 C．x2﹣x+2=0 D．x2﹣x﹣2=0‎ ‎4．（4分）方程组的解是（　　）‎ A． B． C． D．‎ ‎5．（4分）如图，已知∠BDA=∠CDA，则不一定能使△ABD≌△ACD的条件是（　　）‎ A．BD=DC B．AB=AC C．∠B=∠C D．∠BAD=∠CAD ‎6．（4分）若⊙O1与⊙O2相交于两点，且圆心距O1O2=5cm，则下列哪一选项中的长度可能为此两圆的半径？（　　）‎ A．1cm、2cm B．2cm、3cm C．10cm、15cm D．2cm、5cm ‎　‎ 二．填空题：（本大题共12题，每题4分，满分48分）‎ ‎7．（4分）计算：a5÷a2=　　．‎ ‎8．（4分）分解因式：3x2﹣6x=　　．‎ ‎9．（4分）不等式组的解集是　　．‎ ‎10．（4分）函数y=的定义域是　　．‎ ‎11．（4分）二次函数y=x2﹣2x+b的对称轴是直线x=　　．‎ ‎12．（4分）袋子里有4个黑球，m个白球，它们除颜色外都相同．经过大量实验，从中任取一个球恰好是黑球的概率是，则m的值是　　．‎ ‎13．（4分）某中学九（1）班5个同学在体育测试“1分钟跳绳”项目中，跳绳个数如下：126，134，118，152，148．这组数据中，中位数是　　．‎ ‎14．（4分）某企业2013年的年利润为100万元，2014年和2015年连续增长，且这两年的增长率相同，据统计2015年的年利润为125万元．若设这个相同的增长率为x，那么可列出的方程是　　．‎ ‎15．（4分）如图，AB∥DE，△ACB是等腰直角三角形，且∠C=90°，CB的延长线交DE于点G，则∠CGE=　　度．‎ ‎16．（4分）如图，在△ABC中，点D在AC边上且AD：DC=1：2，若，，那么=　　（用向量、表示）．‎ ‎17．（4分）在平面直角坐标系xOy中，⊙C的半径为r，点P是与圆心C不重合的点，给出如下定义：若点P′为射线CP上一点，满足CP•CP′=r2，则称点P′为点P关于⊙C的反演点．如图为点P及其关于⊙C的反演点P′的示意图．写出点M （，0）关于以原点O为圆心，1为半径的⊙O的反演点M′的坐标　　．‎ ‎18．（4分）如图，底角为α的等腰△ABC绕着点B顺时针旋转，使得点A与边BC上的点D重合，点C与点E重合，联结AD、CE．已知tanα=，AB=5，则CE=　　．‎ ‎　‎ 三．解答题：（本大题共7题，满分78分）‎ ‎19．（10分）计算：cos30°+|1﹣|﹣（）﹣1．‎ ‎20．（10分）解方程：．‎ ‎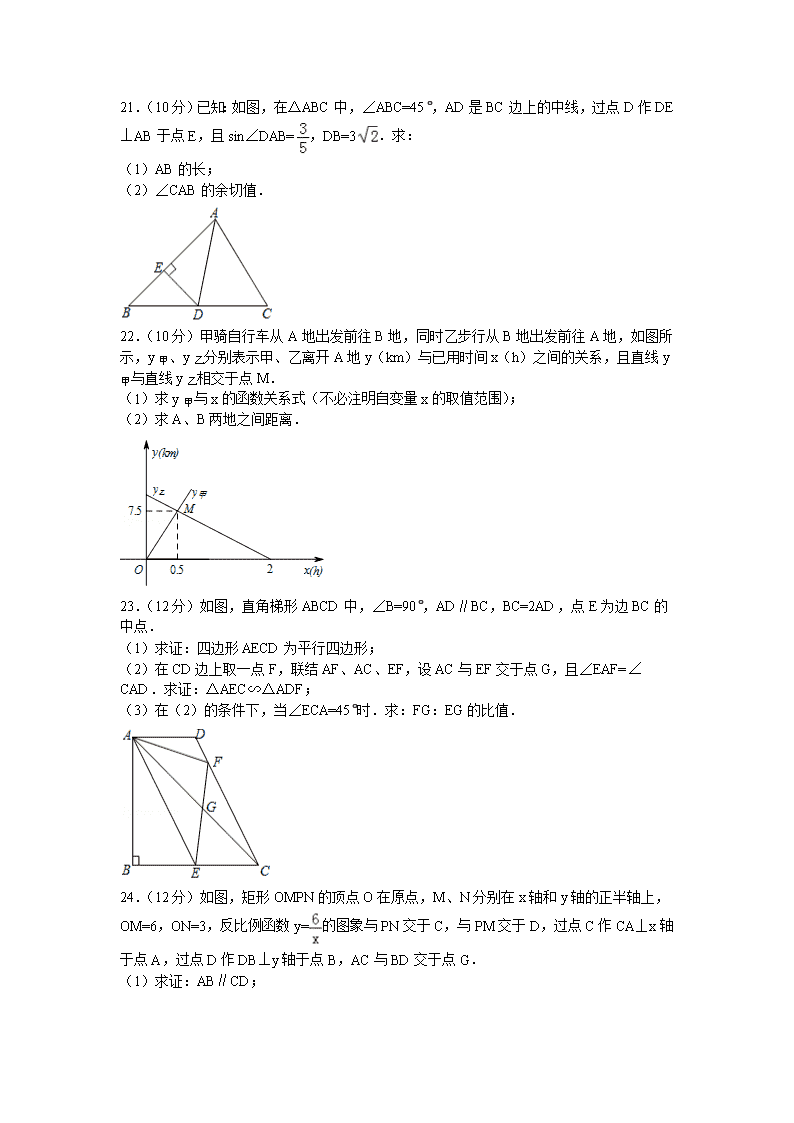21．（10分）已知：如图，在△ABC中，∠ABC=45°，AD是BC边上的中线，过点D作DE⊥AB于点E，且sin∠DAB=，DB=3．求：‎ ‎（1）AB的长；‎ ‎（2）∠CAB的余切值．‎ ‎22．（10分）甲骑自行车从A地出发前往B地，同时乙步行从B地出发前往A地，如图所示，y甲、y乙分别表示甲、乙离开A地y（km）与已用时间x（h）之间的关系，且直线y甲与直线y乙相交于点M．‎ ‎（1）求y甲与x的函数关系式（不必注明自变量x的取值范围）；‎ ‎（2）求A、B两地之间距离．‎ ‎23．（12分）如图，直角梯形ABCD中，∠B=90°，AD∥BC，BC=2AD，点E为边BC的中点．‎ ‎（1）求证：四边形AECD为平行四边形；‎ ‎（2）在CD边上取一点F，联结AF、AC、EF，设AC与EF交于点G，且∠EAF=∠CAD．求证：△AEC∽△ADF；‎ ‎（3）在（2）的条件下，当∠ECA=45°时．求：FG：EG的比值．‎ ‎24．（12分）如图，矩形OMPN的顶点O在原点，M、N分别在x轴和y轴的正半轴上，OM=6，ON=3，反比例函数y=的图象与PN交于C，与PM交于D，过点C作CA⊥x轴于点A，过点D作DB⊥y轴于点B，AC与BD交于点G．‎ ‎（1）求证：AB∥CD；‎ ‎（2）在直角坐标平面内是否若存在点E，使以B、C、D、E为顶点，BC为腰的梯形是等腰梯形？若存在，求点E的坐标；若不存在请说明理由．‎ ‎25．（14分）如图，在△ABC中，AB=AC=6，BC=4，⊙B与边AB相交于点D，与边BC相交于点E，设⊙B的半径为x．‎ ‎（1）当⊙B与直线AC相切时，求x的值；‎ ‎（2）设DC的长为y，求y关于x的函数解析式，并写出定义域；‎ ‎（3）若以AC为直径的⊙P经过点E，求⊙P与⊙B公共弦的长．‎ ‎　‎ ‎2016年上海市闸北区中考数学二模试卷 参考答案 ‎　‎ 一．选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．C；2．A；3．C；4．B；5．B；6．D；‎ ‎　‎ 二．填空题：（本大题共12题，每题4分，满分48分）‎ ‎7．a3；8．3x（x-2）；9．1＜x＜3；10．x≤1；11．1；12．4；13．134；14．100（1+x）2=125；15．135；16．2+2；17．（2，0）；18．；‎ ‎　‎ 三．解答题：（本大题共7题，满分78分）‎ ‎19．　　　；20．　　　；21．　　　；22．　　　；23．　　　；24．　　　；25．　　　；‎ ‎　‎