2020年中考数学专题复习卷 几何图形的动态问题精编（含解析） 31页

几何图形的动态问题精编 ‎1.如图，平行四边形ABCD中，AB= cm，BC=‎2cm，∠ABC=45°，点P从点B出发，以‎1cm/s的速度沿折线BC→CD→DA运动，到达点A为止，设运动时间为t(s)，△ABP的面积为S(cm2)，则S与t的大致图象是（   ） ‎ A.                  B.                  C.                  D. ‎ ‎【答案】A ‎ ‎【解析】 ：分三种情况讨论： ①当0≤t≤2时，过A作AE⊥BC于E．∵∠B=45°，∴△ABE是等腰直角三角形．∵AB= ，∴AE=1，∴S= BP×AE= ×t×1= t； ②当2＜t≤ 时，S=   = ×2×1=1； ③当 ＜t≤ 时，S= AP×AE= ×（ -t）×1= （ -t）． 故答案为：A． 【分析】根据题意分三种情况讨论：①当0≤t≤2时，过A作AE⊥BC于E；②当2＜t≤ 2 +时；③当 2 + ＜t≤ 4 +时，分别求出S与t的函数解析式，再根据各选项作出判断，即可得出答案。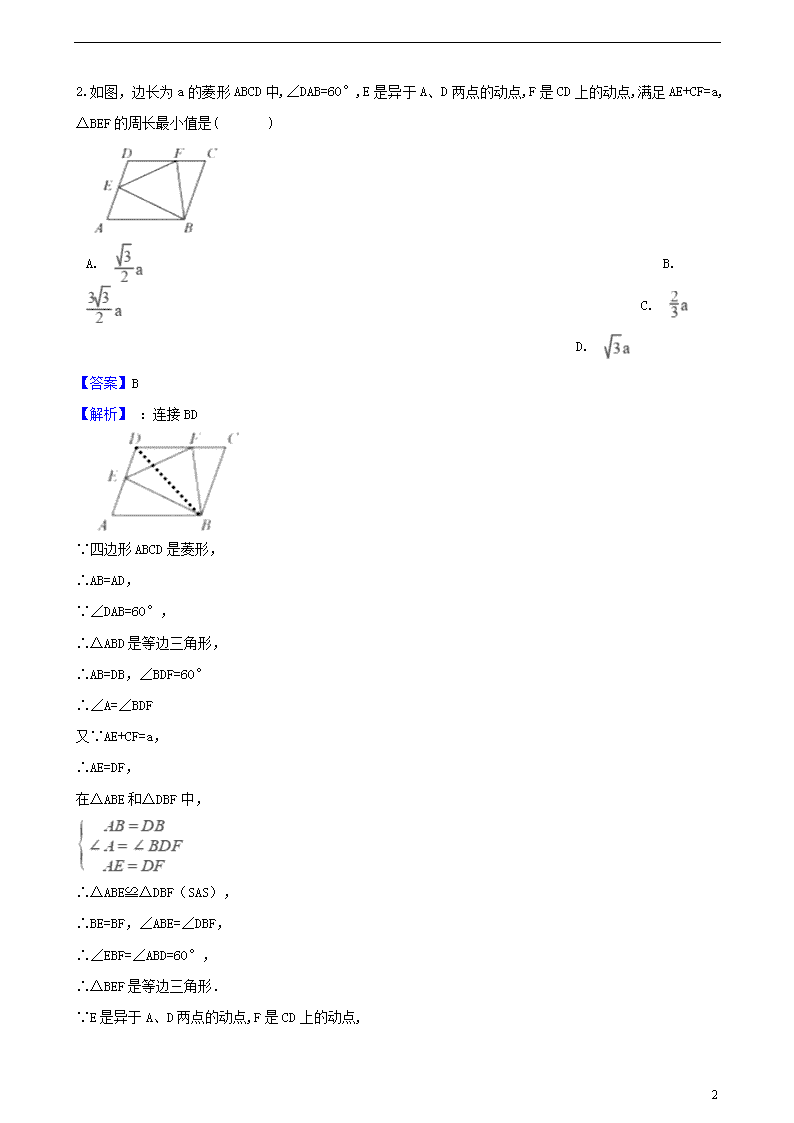‎ 31‎ ‎2.如图，边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a,△BEF的周长最小值是(    ) ‎ A.                                      B.                                      C.                                      D. ‎ ‎【答案】B ‎ ‎【解析】 ：连接BD ∵四边形ABCD是菱形， ∴AB=AD， ∵∠DAB=60°， ∴△ABD是等边三角形， ∴AB=DB，∠BDF=60° ∴∠A=∠BDF 又∵AE+CF=a， ∴AE=DF， 在△ABE和△DBF中， ∴△ABE≌△DBF（SAS）， ∴BE=BF，∠ABE=∠DBF， ∴∠EBF=∠ABD=60°， ∴△BEF是等边三角形． ∵E是异于A、D两点的动点,F是CD上的动点, ‎ 31‎ 要使△BEF的周长最小，就是要使它的边长最短 ∴当BE⊥AD时，BE最短 在Rt△ABE中，BE== ∴△BEF的周长为 【分析】根据等边三角形的性质及菱形的性质，证明∠A=∠BDF，AE=DF，AB=AD，就可证明△ABE≌△DBF，根据全等三角形的性质，可证得BE=BF，∠ABE=∠DBF，再证明△BEF是等边三角形，然后根据垂线段最短，可得出当BE⊥AD时，BE最短，利用勾股定理求出BE的长，即可求出△BEF的周长。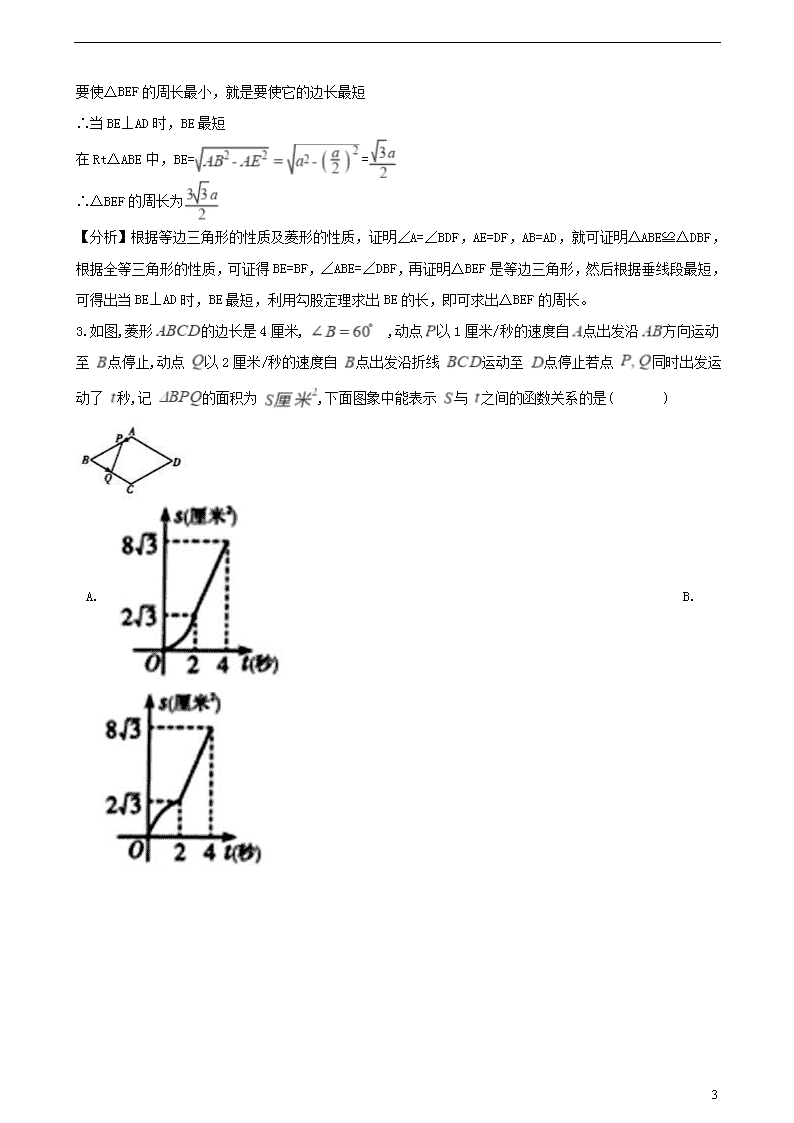‎ ‎3.如图,菱形 的边长是4厘米,  ,动点 以1厘米/秒的速度自 点出发沿 方向运动至 点停止,动点 以2厘米/秒的速度自 点出发沿折线 运动至 点停止若点 同时出发运动了 秒,记 的面积为 ,下面图象中能表示 与 之间的函数关系的是(    ) ‎ A.                            B.  ‎ 31‎ C.                                D. ‎ ‎【答案】D ‎ ‎【解析】 当0≤t＜2时，S=2t× ×（4-t）=- t2+4 t； 当2≤t＜4时，S=4× ×（4-t）=-2 t+8 ； 只有选项D的图形符合． 故答案为：D． 【分析】分别求出当0≤t＜2时和当2≤t＜4时，s与t的函数解析式，再根据各选项的图像逐一判断即可。‎ ‎4.如图,矩形ABCD,R是CD的中点,点M在BC边上运动,E，F分别为AM，MR的中点,则EF的长随M点的运动(      ) ‎ A. 变短                                  B. 变长                                  C. 不变                                  D. 无法确定 ‎【答案】C ‎ 31‎ ‎【解析】 ：∵E，F分别为AM，MR的中点, ∴EF是△ANR的中位线 ∴EF= AR ∵R是CD的中点，点M在BC边上运动 ∴AR的长度一定 ∴EF的长度不变。 故答案为：C【分析】根据已知E，F分别为AM，MR的中点,，可证得EF是△ANR的中位线，根据中位线定理，可得出EF= AR，根据已知可得出AR是定值，因此可得出EF也是定值，可得出结果。‎ ‎5.如图甲，A，B是半径为1的⊙O上两点，且OA⊥OB．点P从A出发，在⊙O上以每秒一个单位的速度匀速运动，回到点A运动结束．设运动时间为x，弦BP的长度为y，那么如图乙图象中可能表示y与x的函数关系的是（   ） ‎ A. ①                                     B. ④                                     C. ①或③                                     D. ②或④‎ ‎【答案】C ‎ ‎【解析】 当点P顺时针旋转时，图象是③，当点P逆时针旋转时，图象是①， 故答案为①③. 故答案为：C． 【分析】由题意知PB的最短距离为0，最长距离是圆的直径；而点P从A点沿顺时针旋转和逆时针旋转后与点B的距离有区别，当点P从A点沿顺时针旋转时，弦BP的长度y的变化是：从AB的长度增大到直径的长，然后渐次较小至点B为0，再从点B运动到点A，则弦BP的长度y由0增大到AB的长； 当点P从A点沿逆时针旋转时，弦BP的长度y的变化是：从AB的长度减小到0，再由0增大到直径的长，最后由直径的长减小到AB的长。‎ 31‎ ‎6.如图，一块等边三角形的木板，边长为1，现将木板沿水平线翻滚，那么B点从开始至结束所走过的路径长度为________．‎ ‎【答案】‎ ‎【解析】 ：从图中发现：B点从开始至结束所走过的路径长度为两段弧长即第一段= ，第二段= ． 故B点从开始至结束所走过的路径长度= + = ． 故答案为： 【分析】B点的运动路径是2个圆心角是120度的扇形的弧长，根据弧长公式求解。‎ ‎7.如图，长方形ABCD中，AB=‎4cm，BC=‎3cm，点E是CD的中点，动点P从A点出发，以每秒‎1cm的速度沿A→B→C→E 运动，最终到达点E．若点P运动的时间为x秒，那么当x= ________时，△APE的面积等于5 ． ‎ ‎【答案】或5 ‎ ‎【解析】 ①如图1， 当P在AB上时， ∵△APE的面积等于5， ∴ x⋅3=5， x= ； ②当P在BC上时， ‎ 31‎ ‎ ∵△APE的面积等于5， ∴ ， ∴3×4−  (3+4−x)×2− ×2×3− ×4×(x−4)=5， x=5； ③当P在CE上时， ∴  (4+3+2−x)×3=5， x= <3+4+2，此时不符合； 故答案为： 或5. 【分析】先对点P所在不同线段的区间进行分类讨论，再结合实际情况与所得结果进行对比从而判断结果的合理性.‎ ‎8.如图，在矩形 中， 点 同时从点 出发，分别在 ， 上运动，若点 的运动速度是每秒2个单位长度，且是点 运动速度的2倍，当其中一个点到达终点时，停止一切运动．以 为对称轴作 的对称图形 ．点 恰好在 上的时间为________秒．在整个运动过程中， 与矩形 重叠部分面积的最大值为________． ‎ ‎【答案】；‎ ‎【解析】 ：（1）如图，当B′与AD交于点E，作FM⊥AD于F， ∴∠DFM=90°． ∵四边形ABCD是矩形， ∴CD=AB．AD=BC．∠D=∠C=90°． ‎ 31‎ ‎∴四边形DCMF是矩形， ∴CD=MF． ∵△MNB与△MNE关于MN对称， ∴△MNB≌△MNE， ∴ME=MB，NE=BN． ∵BN=t，BM=2t， ∴EN=t，ME=2t． ∵AB=6，BC=8， ∴CD=MF=6，CB=DA=8．AN=6-t 在Rt△MEF和Rt△AEN中，由勾股定理，得（1） EF=AE= ∴＋=2t 解得  ：t= （2）如图， ∵△MNE与△MNB关于MN对称， ∴∠MEN=∠MBN=90°． ∵∠MEN+∠MBN+∠EMB+∠ENB=360°， ∴∠EMB+∠ENB=180°． ∵∠ENA+∠ENB=180°， ∴∠ENA=∠EMB． ∵tan∠ENA= ∴tan∠EMB= ∵四边形ABCD是矩形， ∴AD∥BC， ∴∠EFG=∠EMB． ‎ 31‎ ‎∵BN=t，BM=2t， ∴EN=t，ME=2t． ∵AB=6，BC=8， ∴CD=MF=6，CB=DA=8．AN=6  ∴GA=(6-t)  GN=(6-t) ∵EG=EN-GN=t-(6-t)= ∴EF=()×=2t- ∴当时， S=t2-(2t-)()=-(t-6)2+ ∴t=4时，s最大=. 当0＜t≤时，S=t2 ∴t=时，S最大=. ∵＞ ∴最大值为【分析】（1）如图，当B′与AD交于点E，作FM⊥AD于F，根据矩形的性质得出CD=AB．AD=BC．∠D=∠C=90°．进而判断出四边形DCMF是矩形，根据矩形的对边相等得出CD=MF．根据翻折的性质得出△MNB≌△MNE，根据全等三角形对应边相等得出ME=MB，NE=BN．然后表示出EN=t，ME=2t．CD=MF=6，CB=DA=8．AN=6-t，在Rt△MEF和Rt△AEN中，由勾股定理EF,AE的长，根据线段的和差得出方程，求解得出t的 值； （2）根据翻折的性质得出∠MEN=∠MBN=90°．根据四边形的内角和，邻补角定义及等量代换得出∠ENA=∠EMB．根据等角的同名三角函数值相等得出tan∠ENA=tan∠EMB=， 根据矩形的性质得出∠EFG=∠EMB．EN=t，ME=2t．CD=MF=6，CB=DA=8．AN=6-t，进而表示出GA,GN,EG,EF,的长，当 < t ≤ 4 时，与当0＜t≤ 时，分别求出S的值，再比大小即可得出答案。‎ ‎9.如图，在△ABC中，BC＝AC＝5，AB＝8，CD为AB边的高，点A在x轴上，点B在y轴上，点C在第一象限，若A从原点出发，沿x轴向右以每秒1个单位长的速度运动，则点B随之沿y轴下滑，并带动△ABC 31‎ 在平面内滑动，设运动时间为t秒，当B到达原点时停止运动 ‎ ‎（1）连接OC，线段OC的长随t的变化而变化，当OC最大时，t＝________； ‎ ‎（2）当△ABC的边与坐标轴平行时，t＝________。 ‎ ‎【答案】（1） （2）t＝ ‎ ‎【解析】 （1）如图： 当 三点共线时， 取得最大值，       （ 2 ）分两种情况进行讨论：①设  时，CA⊥OA， ∴CA∥y轴， ∴∠CAD=∠ABO. 又   ∴Rt△CAD∽Rt△ABO， ∴  即   解得   ②设 时，   ‎ 31‎ ‎∴CB∥x轴， Rt△BCD∽Rt△ABO， ∴  即     综上可知,当以点C为圆心,CA为半径的圆与坐标轴相切时,t的值为 或   故答案为：     或   【分析】（1）当 O , C , D 三点共线时，OC取得最大值，此时OC是线段AB的中垂线， 根据中垂线的性质，及勾股定理得出OA =OB = 4 ,  然后根据时间等于路程除以速度即可得出答案； （ 2 ）分两种情况进行讨论：①设OA = t 1  时，CA⊥OA，故CA∥y轴，然后判断出Rt△CAD∽Rt△ABO，根据相似三角形对应边成比例得出AB∶CA = AO∶CD ,从而得出答案；②设 A O = t 2 时，BC ⊥OB ，故CB∥x轴，然后判断出Rt△BCD∽Rt△ABO，根据相似三角形对应边成比例得出BC∶AB=BD∶ AO, 从而得出答案.‎ ‎10.如图，在平面直角坐标系中，A(4，0)、B(0，-3)，以点B为圆心、2 为半径的⊙B上 有一动点P.连接AP，若点C为AP的中点，连接OC，则OC的最小值为________． ‎ ‎【答案】‎ ‎【解析】 ：作A关于y轴的对称点A′， 则A′（－4，0）， ∴OC是△AA′P的中位线，当A′P取最小值时，OC取最小值．连接A′B交⊙B于点P，此时A′P 31‎ 最小． 在Rt△OA′B中，OA′=4，OB=3， ∴A′B=5，∴A′P=5-2=3，∴OC= ， ∴OC的最小值 ． 故答案为： ． 【分析】作A关于y轴的对称点A′，可得出点A′的坐标，可证得OC是△AA′P的中位线，因此当A′P取最小值时，OC取最小值．连接A′B交⊙B于点P，此时A′P最小，再利用勾股定理求出A′B，再根据圆的半径求出A′P的长，利用三角形的中位线定理，即可求出OC的最小值 。‎ ‎11.已知矩形 中， 是 边上的一个动点，点 ， ， 分别是 ， ， 的中点. ‎ ‎（1）求证： ； ‎ ‎（2）设 ，当四边形 是正方形时，求矩形 的面积. ‎ ‎【答案】（1）解：∵点F,H分别是BC,CE的中点， ∴FH∥BE， ． ∴ ． 又∵点G是BE的中点， ∴ ． 又∵ ， ∴△BGF ≌ △FHC． （2）解：当四边形EGFH是正方形时，可知EF⊥GH且 ∵在△BEC中，点G，H分别是BE,EC的中点, ∴  且GH∥BC, ∴ 又∵AD∥BC, AB⊥BC, ‎ 31‎ ‎∴ ， ∴ ． ‎ ‎【解析】【分析】（1）根据点F,H分别是BC,CE的中点，可证得FH是△BCE的中位线，就可证得FH∥BE， FH=BE 再根据点G是BE的中点，得出FH=BG，就可证得结论。 （2）当四边形EGFH是正方形时，可知EF⊥GH且 E F = G H ，根据已知在△BEC中，点G，H分别是BE,EC的中点，可证得GH是△BCE的中位线，可求出GH的长及GH∥BC，再根据AD∥BC, AB⊥BC，可证得AB=GH，然后利用矩形的面积公式，即可求解。‎ ‎12.如图，在△ABC中，∠C＝90°，AC＝‎4cm，BC＝‎5cm，点D在BC上，且CD＝‎3cm.动点P、Q分别从A、C两点同时出发，其中点P以‎1cm/s的速度沿AC向终点C移动；点Q以 cm/s的速度沿CB向终点B移动．过点P作PE∥CB交AD于点E，设动点的运动时间为x秒． ‎ ‎（1）用含x的代数式表示EP； ‎ ‎（2）当Q在线段CD上运动几秒时，四边形PEDQ是平行四边形； ‎ ‎（3）当Q在线段BD(不包括点B、点D)上运动时，求当x为何值时，四边形EPDQ面积等于 . ‎ ‎【答案】（1）解:如图所示， ∵PE∥CB， ∴∠AEP＝∠ADC.  又∵∠EAP＝∠DAC， ∴△AEP∽△ADC， ∴ ＝ ，  ‎ 31‎ ‎∴ ＝ ， ∴EP＝ x. （2）解：由四边形PEDQ1是平行四边形，可得EP＝DQ1.  即 x＝3－ x，所以x＝1.5. ∵0＜x＜2.4 ∴当Q在线段CD上运动1.5秒时，四边形PEDQ是平行四边形 （3）解： S四边形EPDQ2＝  ( x＋ x－3)·(4－x)＝－x2＋ x－6， ∵四边形EPDQ面积等于 ， ∴－x2＋ x－6＝ ， 整理得：2x2－11x＋15＝0. 解得：x＝3或x＝2.5， ∴当x为3或2.5时，四边形EPDQ面积等于 . ‎ ‎【解析】【分析】（1）抓住已知条件PE∥CB，证明△AEP∽△ADC，再根据相似三角形的性质得出对应边成比例，可得出EP的长。 （2）根据已知可知PE∥CB，要证四边形PEDQ是平行四边形，则EP＝DQ1 ， 建立关于x的方程，求出x的值，再写出x的取值范围即可。 （3）根据PE∥CB，可证得四边形EPDQ是梯形，根据梯形的面积=， 建立关于x的方程，再解方程求解即可。‎ ‎13.如图1，图2中，正方形ABCD的边长为6，点P从点B出发沿边BC—CD以每秒2个单位长的速度向点D匀速运动，以BP为边作等边三角形BPQ，使点Q在正方形ABCD内或边上，当点Q恰好运动到AD边上时，点P停止运动。设运动时间为t秒（t≥0）。      ‎ ‎（1）当t＝2时，点Q到BC的距离＝________； ‎ ‎（2）当点P在BC边上运动时，求CQ的最小值及此时t的值； ‎ 31‎ ‎（3）若点Q在AD边上时，如图2，求出t的值； ‎ ‎（4）直接写出点Q运动路线的长。 ‎ ‎【答案】（1）解： （2）解：点P在BC边上运动时，有 ，根据垂线段最短，当 时，CQ最小， 如图，在直角三角形BCQ中， ，     ∴   ∴   ∴ （3）解：若点Q在AD边上，则   ∵   ∴Rt△BAQ≌Rt△BCP（HL）, ∴   ∴   ∵ ，且由勾股定理可得， ∴ 解得： （不合题意，舍去）， ∴ （4）解：点Q运动路线的长等于点 运动的路线长：   ‎ 31‎ ‎【解析】【解答】 如图： 过点 作   当 时，   是等边三角形，     故答案为： 【分析】(1）过点 Q 作QE⊥BC,  根据路程等于速度乘以时间，由 t = 2 ， 得出BP的长，根据等边三角形的性质得出BQ = 4 , ∠QBE = 60 ∘ ,在Rt△BPQ中，根据正弦函数的定义即可得出QE的长； （2）点P在BC边上运动时，有 ∠QBC = 60 ° ，根据垂线段最短，当 CQ⊥BQ 时，CQ最小，如图，在直角三角形BCQ中， ∠QBC= 60 ° ，从而得出BQ的长度，根据等边三角形的性质得出BP=BQ=3，根据时间等于路程除以速度，从而得出t的值，再根据正切函数的定义，即可得出CQ的长； （3）若点Q在AD边上，则 C P = 2 t − 6 ，  首先利用HL判断出Rt△BAQ≌Rt△BCP，根据全等三角形对应边相等得出A Q = C P = 2 t − 6 ,  进而得出DQ =DP= 12 − 2 t , 由 BP = PQ ，且由勾股定理可得，DQ 2 + DP 2 =QP 2 ， BC 2 +CP2 =BP 2,得出关于t的方程，求解并检验即可得出t的值； （4）根据题意点Q运动路线的长等于点 P 运动的路线长，由路程等于速度乘以时间即可得出答案。‎ ‎14.已知：如图①，在平行四边形ABCD中，AB=12，BC=6，AD⊥BD．以AD为斜边在平行四边形AB CD的内部作Rt△AED，∠EAD=30°，∠AED=90°． ‎ ‎（1）求△AED的周长； ‎ 31‎ ‎（2）若△ AED以每秒2个单位长度的速度沿DC向右平行移动，得到△AE0D0 ， 当A0D0与BC重合时停止移动，设运动时间为t秒，△A0E0D0与△BDC重叠的面积为S，请直接写出 S与t之间的函数关系式，并写出t的取值范围； ‎ ‎（3）如图②，在（2）中，当△AED停止移动后得到△BEC，将△BEC绕点C按顺时针方向旋转α（0°＜α＜180°），在旋转过程中，B的对应点为B1 ， E的对应点为E1 ， 设直线B1E1与直线BE交于点P、与直线CB交于点Q．是否存在这样的α，使△BPQ为等腰三角形？若存在，求出α的度数；若不存在，请说明理由． ‎ ‎【答案】（1）解：（1）∵四边形ABCD是平行四边形， ∴AD=BC=6． 在Rt△ADE中，AD=6，∠EAD=30°， ∴AE=AD•cos30°=6×=3， DE=AD•sin30°=6×=3， ∴△AED的周长为：6+3+3=9+3。 （2）解：在△AED向右平移的过程中： （I）当0≤t≤1.5时，如答图1所示，此时重叠部分为△D0NK． ∵DD0=2t，∴ND0=DD0•sin30°=t，NK=ND0÷tan30°=t， ∴S=S△D0NK=1ND0•NK=t•t=t2； （II）当1.5