中考数学常见几何模型简介 14页

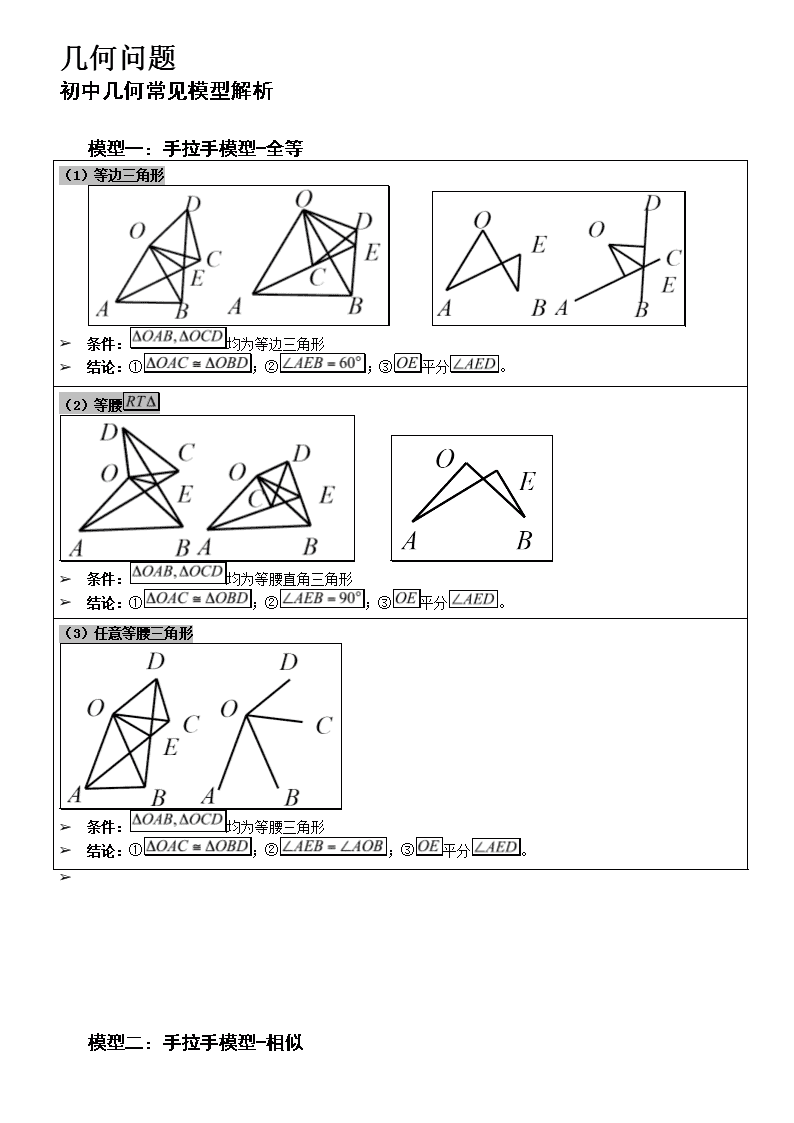
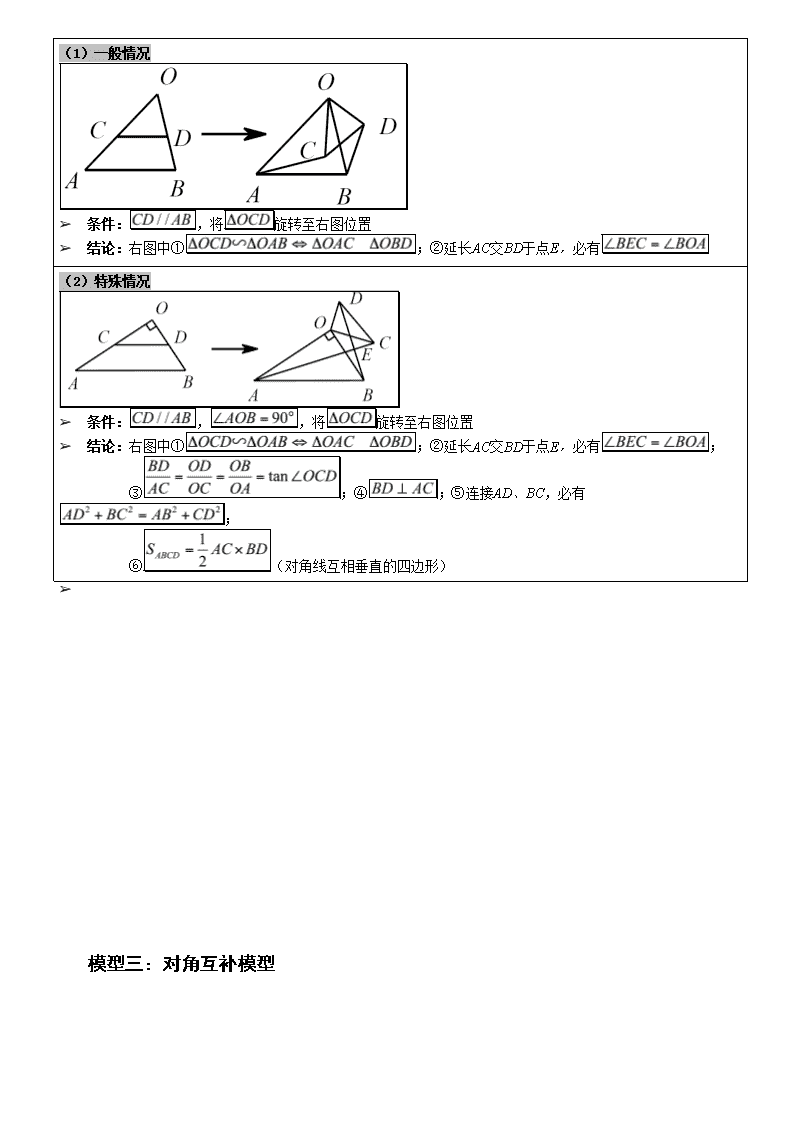
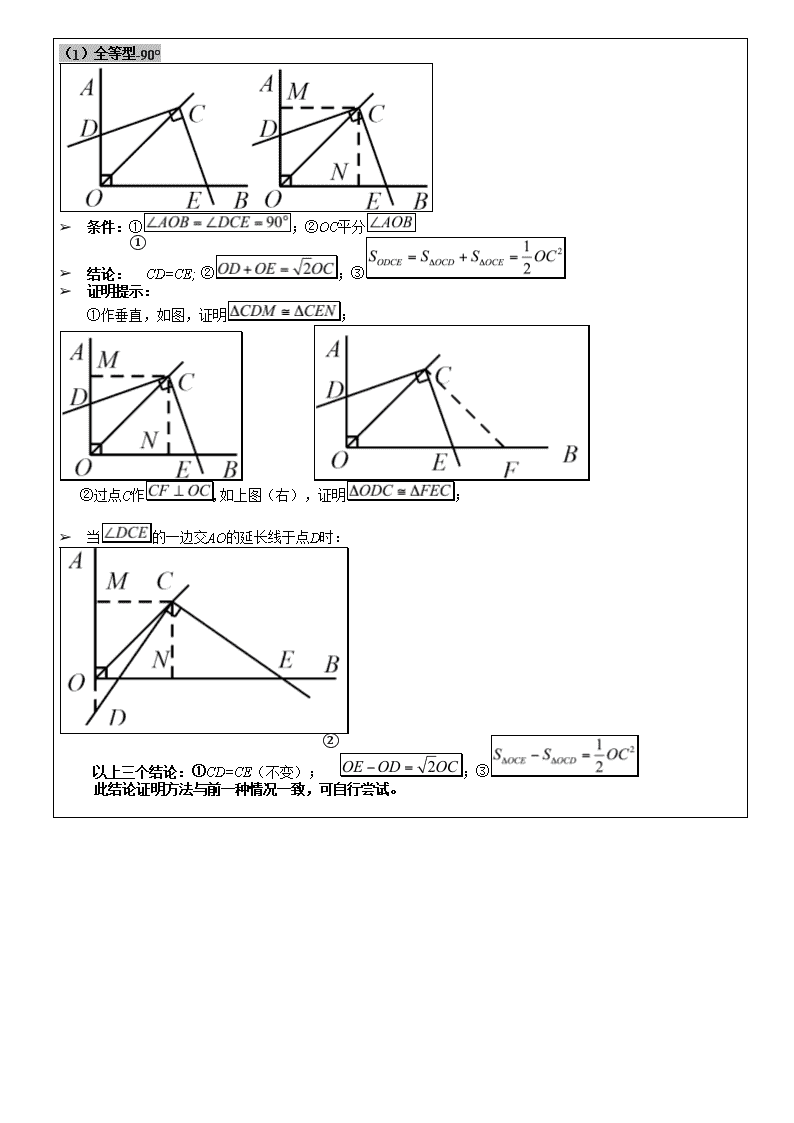
几何问题 初中几何常见模型解析 模型一：手拉手模型-全等 （1）等边三角形 ➢ 条件： 均为等边三角形 ➢ 结论：① ；② ；③ 平分 。 （2）等腰 ➢ 条件： 均为等腰直角三角形 ➢ 结论：① ；② ；③ 平分 。 （3）任意等腰三角形 ➢ 条件： 均为等腰三角形 ➢ 结论：① ；② ；③ 平分 。 ➢ 模型二：手拉手模型-相似 （1）一般情况 ➢ 条件： ，将 旋转至右图位置 ➢ 结论：右图中① ；②延长 AC 交 BD 于点 E，必有 （2）特殊情况 ➢ 条件： ， ，将 旋转至右图位置 ➢ 结论：右图中① ；②延长 AC 交 BD 于点 E，必有 ； ③ ； ④ ； ⑤ 连 接 AD 、 BC ， 必 有 ； ⑥ （对角线互相垂直的四边形） ➢ 模型三：对角互补模型 （1）全等型-90° ➢ 条件：① ；②OC 平分 ➢ 结论：①CD=CE; ② ；③ ➢ 证明提示： ①作垂直，如图，证明 ； ②过点 C 作 ,如上图（右），证明 ； ➢ 当 的一边交 AO 的延长线于点 D 时： 以上三个结论：①CD=CE（不变）；② ；③ 此结论证明方法与前一种情况一致，可自行尝试。 （2）全等型-120° ➢ 条件：① ；② 平分 ； ➢ 结论：① ；② ；③ ➢ 证明提示：①可参考“全等型-90°”证法一； ②如图：在 OB 上取一点 F，使 OF=OC，证明 为等边三角形。 ➢ 当 的一边交 AO 的延长线于点 D 时（如上图右）： 原结论变成：① ； ② ； ③ ； 可参考上述第②种方法进行证明。 （3）全等型-任意角 ➢ 条件：① ；② ； ➢ 结 论 ： ① 平 分 ； ② ； ③ . ➢ 当 的一边交 AO 的延长线于点 D 时（如右上图）： 原结论变成：① ； ② ； ③ ； 可参考上述第②种方法进行证明。 ◇ 请思考初始条件的变化对模型的影响。 ➢ 如图所示，若将条件“ 平分 ”去掉，条件①不变， 平分 ，结论变化如下： 结论：① ；② ；③ . ➢ 对角互补模型总结： ①常见初始条件：四边形对角互补； 注意两点：四点共圆及直角三角形斜边中线； ②初始条件“角平分线”与“两边相等”的区别； ③两种常见的辅助线作法； ④注意下图中 平分 时， 相等是如何推导的？ 模型四：角含半角模型 90° （1）角含半角模型 90°-1 ➢ 条件：①正方形 ；② ； ➢ 结论：① ；② 的周长为正方形 周长的一半； 也可以这样： ➢ 条件：①正方形 ；② ➢ 结论： （2）角含半角模型 90°-2 ➢ 条件：①正方形 ；② ； ➢ 结论： ➢ 辅助线如下图所示： （3）角含半角模型 90°-3 ➢ 条件：① ；② ； ➢ 结论： 若 旋转到 外部时，结论 仍然成立。 （4）角含半角模型 90°变形 ➢ 条件：①正方形 ；② ； ➢ 结论： 为等腰直角三角形。 ➢ 模型五：倍长中线类模型 （1）倍长中线类模型-1 ➢ 条件：①矩形 ；② ;③ ； ➢ 结论： 模型提取：①有平行线 ；②平行线间线段有中点 ； 可以构造“8”字全等 。 （2）倍长中线类模型-2 ➢ 条件：①平行四边形 ；② ；③ ；④ . ➢ 结论： ➢ 模型六：相似三角形 360°旋转模型 （1）相似三角形（等腰直角）360°旋转模型-倍长中线法 ➢ 条件：① 、 均为等腰直角三角形；② ➢ 结论：① ；② （1）相似三角形（等腰直角）360°旋转模型-补全法 ➢ 条件：① 、 均为等腰直角三角形；② ； ➢ 结论：① ；② （2）任意相似直角三角形 360°旋转模型-补全法 ➢ 条件：① ；② ;③ 。 ➢ 结论：① ；② （2）任意相似直角三角形 360°旋转模型-倍长法 ➢ 条件：① ；② ;③ 。 ➢ 结论：① ；② ➢ 模型七：最短路程模型 （1）最短路程模型一（将军饮马类） （2）最短路程模型二（点到直线类 1） ➢ 条件：① 平分 ；② 为 上一定点；③ 为 上一动点；④ 为 上一动点； ➢ 求： 最小时， 的位置？ （3）最短路程模型二（点到直线类 2） （4）最短路程模型二（点到直线类 3） ➢ 条件： ➢ 问题： 为何值时， 最小 ➢ 求解方法：① 轴上取 ，使 ；②过 作 ，交 轴于点 ，即为所求； ③ ，即 . （5）最短路程模型三（旋转类最值模型） （6）最短路程模型三（动点在圆上） ➢ 模型八：二倍角模型 ➢ 模型九：相似三角形模型 （1）相似三角形模型-基本型 （2）相似三角形模型-斜交型 （3）相似三角形模型-一线三角型 （4）相似三角形模型-圆幂定理型 ➢