配套K天津专用高考数学总复习专题不等式分项练习含解析理 9页

专题07 不等式 一．基础题组 ‎1.【2005天津，理3】给出下列三个命题 ‎① 若，则 ‎② 若正整数和满足，则 ‎③ 设是圆上的任意一点，圆以为圆心，且半径为1。当时，圆与圆相切 其中假命题的个数为 A、0 B、‎1 C、2 D、3‎ ‎【答案】B 相交。故本命题假命题。‎ 本题答案选B ‎2.【2006天津，理3】设变量、满足约束条件，则目标函数的最小值为（ ）‎ A．　　 　 　B．　　　　　 C．　　　 D． ‎ ‎【答案】B ‎【解析】设变量、满足约束条件在坐标系中画出可行域△ABC，A(2，0)，B(1，1)，C(3，3)，则目标函数的最小值为3，选B.‎ ‎3.【2007天津，理2】设变量满足约束条件则目标函数的最大值为 ( )‎ ‎ A.4 B‎.11 ‎C.12 D.14‎ ‎【答案】B ‎【解析】‎ ‎ 易判断公共区域为三角形区域，求三个顶点坐标为、、，将代入得到最大值为故选B ‎4.【2008天津，理2】设变量满足约束条件，则目标函数的最大值为 ‎(A) 2 (B) 3 (C) 4 (D) 5‎ ‎【答案】D ‎5.【2008天津，理8】已知函数，则不等式的解集是 ‎(A) (B) ‎ ‎(C) (D) ‎ ‎【答案】C ‎ ‎【解析】依题意得 所以，选C．‎ ‎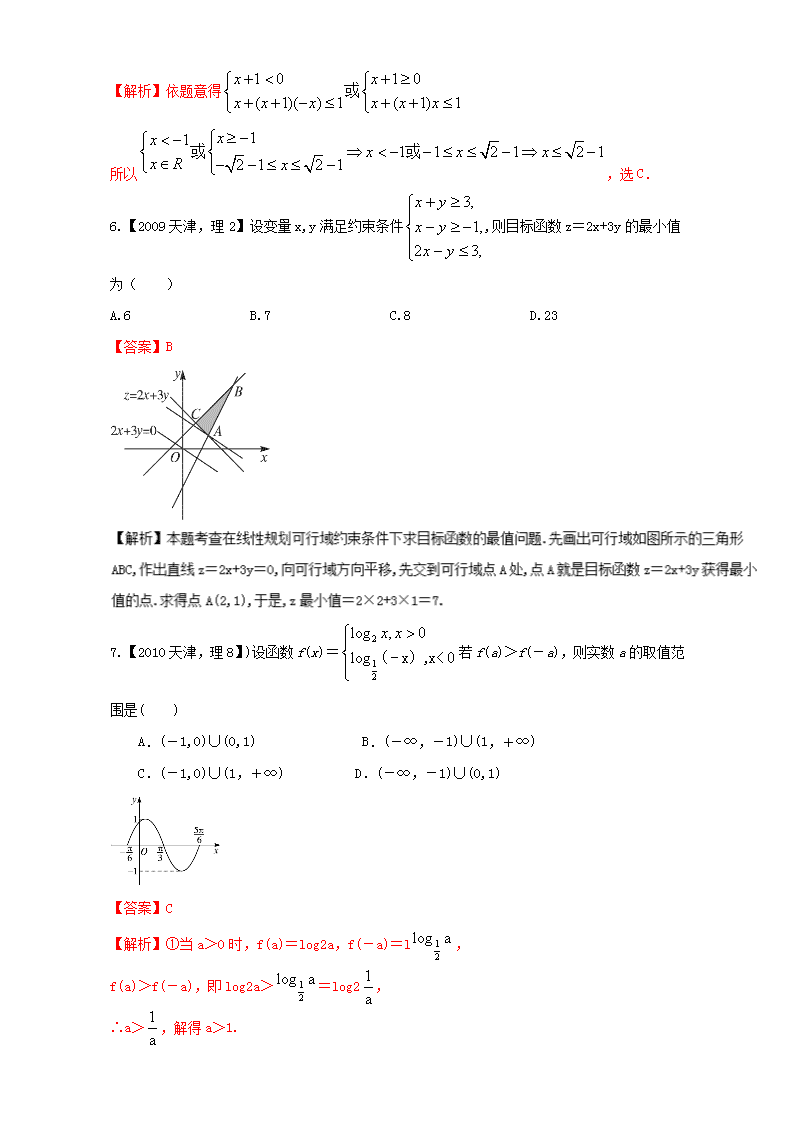6.【2009天津，理2】设变量x,y满足约束条件,则目标函数z＝2x+3y的最小值为（ ）‎ A.6 B‎.7 C.8 D.23‎ ‎【答案】B ‎7.【2010天津，理8】)设函数f(x)＝若f(a)＞f(－a)，则实数a的取值范围是(　　)‎ A．(－1,0)∪(0,1) B．(－∞，－1)∪(1，＋∞)‎ C．(－1,0)∪(1，＋∞) D．(－∞，－1)∪(0,1)‎ ‎【答案】C　‎ ‎【解析】①当a＞0时，f(a)＝log‎2a，f(－a)＝l，‎ f(a)＞f(－a)，即log‎2a＞＝log2，‎ ‎∴a＞，解得a＞1.‎ ‎②当a＜0时，f(a)＝ (－a)，f(－a)＝log2(－a)，‎ f(a)＞f(－a)，即 (－a)＞log2(－a)＝ ，‎ ‎∴－a＜，解得－1＜a＜0.‎ 由①②得－1＜a＜0或a＞1. ‎ ‎8.【2013天津，理2】设变量x，y满足约束条件则目标函数z＝y－2x的最小值为(　　)．‎ A．－7 B．－4‎ C．1 D．2‎ ‎【答案】A ‎9.【2014天津，理2】设变量，满足约束条件则目标函数的最小值为 （　　）‎ ‎（A）2　　 （B）3　 （C）4　　　 （D）5‎ ‎【答案】B．‎ ‎【解析】‎ 试题分析：由题画出如图所示的可行域，由图可知当直线经过点时，‎ ‎，故选B．‎ 考点：1．二元一次不等式组表示的平面区域；2．线性目标函数的最值问题．‎ ‎10. 【2015高考天津，理2】设变量 满足约束条件 ，则目标函数的最大值为( )‎ ‎（A）3 （B）4 （C）18 （D）40‎ ‎【答案】C ‎ ‎ ‎【考点定位】线性规划.‎ ‎11. 【2016高考天津理数】设变量x，y满足约束条件 则目标函数的最小值为 ‎（A） （B）6 （C）10 （D）17‎ ‎【答案】B ‎【解析】‎ ‎【考点】线性规划 ‎【名师点睛】对于线性规划问题，首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线，其次确定目标函数的几何意义，是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等，最后结合图形确定目标函数最值或值域范围.‎ ‎12.【2017天津,理2】设变量满足约束条件则目标函数的最大值为 ‎（A） （B）1 （C） （D）3‎ ‎【答案】D ‎【解析】画出不等式组表示的平面区域（图略），则可行域为四边形及其内部，其中，易得直线过点时取最大值为3，故选D．‎ ‎【考点】线性规划 ‎【名师点睛】线性规划问题有三类：①简单的线性规划，包括画出可行域和考查截距型目标函数的最值，有时考查斜率型或距离型目标函数；②线性规划逆向思维问题，给出最值或最优解个数求参数的取值范围；③线性规划的实际应用．‎ ‎13.【2017天津,理12】若，，则的最小值为___________．‎ ‎【答案】‎ ‎【解析】，（前一个等号成立的条件是后一个等号成立的条件是，两个等号可以同时成立，当且仅当时取等号）．‎ ‎【考点】均值不等式 ‎【名师点睛】利用均值不等式求最值时要灵活运用以下两个公式：①，当且仅当时取等号；②，，当且仅当时取等号．解题时要注意公式的适用条件、等号成立的条件，同时求最值时注意 ‎“1的妙用”．‎ 二．能力题组 ‎1.【2006天津，理15】某公司一年购买某种货物400吨，每次都购买吨，运费为4万元/次，一年的总存储费用为万元，要使一年的总运费与总存储费用之和最小，则 吨．‎ ‎【答案】20　‎ ‎【解析】某公司一年购买某种货物400吨，每次都购买吨，则需要购买次，运费为4万元/次，一年的总存储费用为万元，一年的总运费与总存储费用之和为万元，≥160，当即20吨时，一年的总运费与总存储费用之和最小。‎ ‎2.【2009天津，理10】设0＜b＜1+a.若关于x的不等式(x－b)2＞(ax)2的解集中的整数恰有3个,则（ ）‎ A.－1＜a＜0 B.0＜a＜‎1 C.1＜a＜3 D.3＜a＜6‎ ‎【答案】C 三．拔高题组 ‎1.【2005天津，理20】某人在一山坡P处观看对面山项上的一座铁塔，如图所示，塔高BC = 80（米），塔所在的山高OB = 220（米），OA = 200（米），图中所示的山坡可视为直线l且点P在直线l上，l与水平地面的夹角为a，。试问此人距水平地面多高时，观看塔的视角∠BPC最大（不计此人的身高）。‎ ‎【答案】‎‎60米 由均值不等式：‎ 当且仅当时，即时上式等号成立，这时，点P的纵坐标为 当最大时，最大。‎ 所以，当此人距地面‎60米的时，观看铁塔的视角最大。‎ ‎2.【2013天津，理14】设a＋b＝2，b＞0，则当a＝__________时，取得最小值．‎ ‎【答案】－2‎ ‎【解析】因为a＋b＝2，所以