高考真题空间几何体 12页

‎ 空间几何体和三视图、表面积及体积 ‎1棱柱的体积公式： =Sh，其中S是棱柱的底面积，h为 ‎2棱锥的体积公式：= Sh，其中S是棱锥的底面积，h为高.‎ ‎1．（2016全国一卷（7））如图，学.科网某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是，则它的表面积是 ‎（A）17π （B）18π （C）20π （D）28π ‎ ‎2.（2016全国三卷10）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为 ‎（A） （B） （C）90 （D）81‎ ‎3.（2016全国二卷(7)） 如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为 ‎（A）20π（B）24π（C）28π（D）32π ‎4.（2016浙江9）.某几何体的三视图如图所示（单位：cm），则该几何体的表面积是______cm2,体积是______cm3.‎ ‎5.（2016天津（3））将一个长方形沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为 ‎6.（2016四川）已知某三菱锥的三视图如图所示，则该三菱锥的体积是 。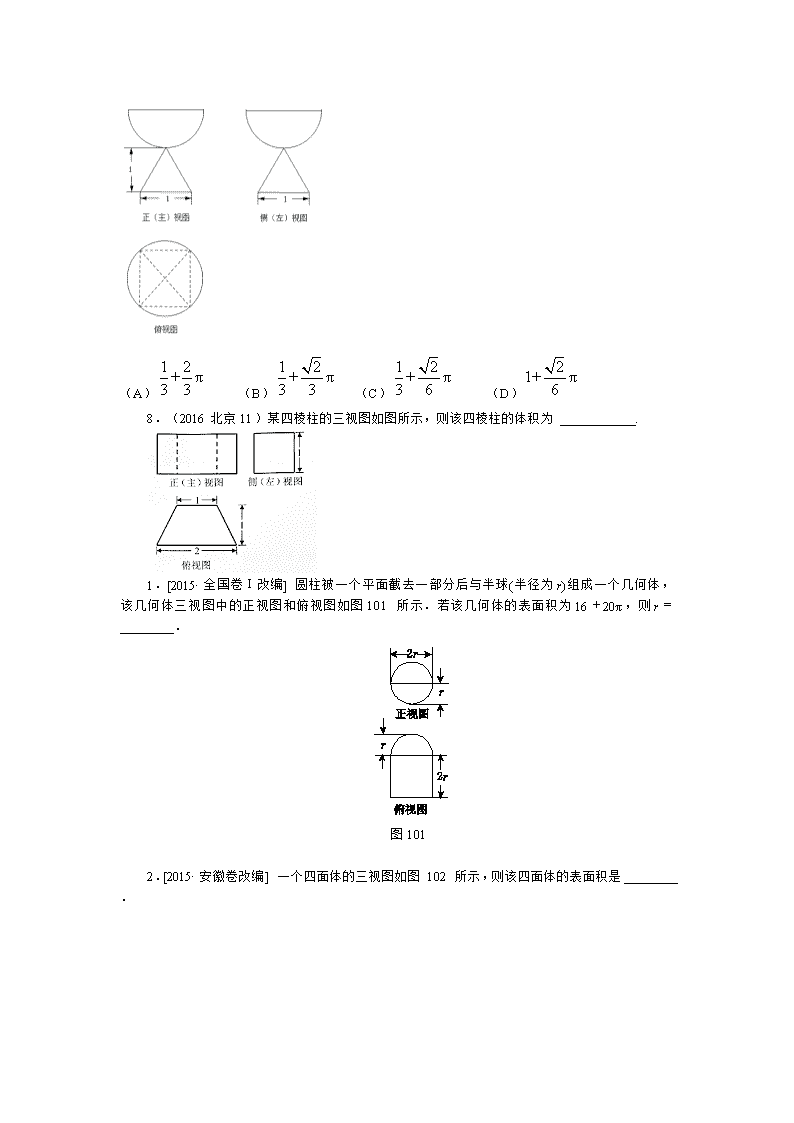‎ ‎7.（2016山东5）一个由半球和四棱锥组成的几何体，其三视图如图所示.则该几何体的体积为 ‎（A） （B） （C） （D）‎ ‎8．（2016北京11）某四棱柱的三视图如图所示，则该四棱柱的体积为___________.‎ ‎1．[2015·全国卷Ⅰ改编] 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图101所示．若该几何体的表面积为16＋20π，则r＝________．‎ 图101‎ ‎2．[2015·安徽卷改编] 一个四面体的三视图如图102所示，则该四面体的表面积是________．‎ ‎　　‎ 图102‎ ‎　3．[2014·浙江卷改编] 某几何体的三视图(单位：cm)如图103所示，则此几何体的表面积是________．‎ ‎　‎ 图103‎ ‎4．[2015·浙江卷改编] 某几何体的三视图如图104所示(单位：cm)，则该几何体的体积是________．‎ 图104‎ ‎5．[2015·重庆卷改编] 某几何体的三视图如图105所示，则该几何体的体积为________．‎ ‎　 ‎ 图105‎ ‎6．[2015·天津卷] 一个几何体的三视图如图106所示(单位：m)，则该几何体的体积为________m3.‎ ‎　 ‎ 图106‎ ‎7．[2015·山东卷改编] 在梯形ABCD中，∠ABC＝，AD∥BC，BC＝2AD＝2AB＝2，将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为________．‎ ‎8．[2015·江苏卷] 现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个．若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为________．‎ ‎9．[2015·上海卷] 若圆锥的侧面积与过轴的截面面积之比为2π，则其母线与轴的夹角的大小为________．‎ ‎10．[2015·全国卷Ⅱ改编] 已知A，B是球O的球面上两点，∠AOB＝90°，C为该球面上的动点．若三棱锥O ABC体积的最大值为36，则球O的表面积为________．‎ 考点一　　　三视图与直观图 题型：选择、填空　　　　　分值：5分 难度：中等 热点：三视图结合相关计算 图107‎ ‎1 在如图107所示的空间直角坐标系Oxyz中，一个四面体的顶点坐标分别是(0，0，2)，(2，2，0)，(1，2，1)，(2，2，2)，给出编号①②③④的四个图，则该四面体的正视图和俯视图分别为(　　)‎ 图108‎ A．①和② B．③和①‎ C．③和④ D．④和② ‎ ‎ [小结] ‎ 找空间几何体的三视图，关键要抓住空间几何体的顶点在投影面上的正投影，再看各棱在投影面上的正投影；根据三视图判断空间几何体的形状，基本方法是根据三视图的画法进行逆向思维，借助已知的空间几何体的结构特点、结合题目要求进行肯定或者否定．要特别注意三视图中“眼见为实、不见为虚”的画法规则．‎ 式题 若某几何体的三视图如图109所示，则此几何体的直观图是(　　)‎ 图109‎ 图1010‎ 考点二　　　几何体的表面积与体积 题型：选择、填空　　分值：5分　　难度：中等 热点：根据空间几何体的三视图计算表面积和体积 图1011‎ ‎2 一个简单几何体的三视图如图1011所示，其中正视图是一个正三角形，俯视图是等腰直角三角形，则该几何体的体积为________，表面积为________．‎ ‎ [小结] 高考试题中求体积和表面积的试题往往与空间几何体的三视图结合，此时要根据空间几何体的三视图还原空间几何体，弄清楚空间几何体的结构再进行计算．体积的计算需要空间几何体的底面积和高，表面积的计算需要把各个面的结构弄清楚，分别计算各个面的面积，再求和．‎ 式题 已知某几何体的三视图如图1012所示，则该几何体的体积是__________，表面积是________．‎ 图1012‎ ‎ 高考易失分题11 三视图、直观图、体积问题的综合 范例 某篮球架的底座的三视图如图1013所示，则其体积为(　　)‎ 图1013‎ A. B．175‎ C．180 D．295＋10 失分分析 该类试题容易把空间几何体的结构弄错，求体积时不能准确割补、求表面积时出现遗漏或重复等错误．‎ 高考预测 某几何体的三视图如图1014所示，其中侧视图是一个边长为2的正三角形，则这个几何体的体积是(　　)‎ 图1014‎ A．2 B. C．3 D．3‎ 考点三　　　多面体与球 题型：选择、填空　　分值：5分　　难度：中等 热点：多面体外接球的表面积和体积计算 图1015‎ ‎3 如图1015所示，在等腰梯形ABCD中，AB＝2CD＝2，∠DAB＝60°，E为AB的中点．将△ADE与△BEC分别沿ED，EC 向上折起，使A，B重合于点P，则三棱锥PDCE的外接球的体积为(　　)‎ A. B. C. D. ‎ [小结] 球中内接一个多面体是高考的一个重要命题点．如果一个多面体内接于一个球，那么它的各个多边形都是圆的内接多边形，球心到各个顶点的距离都等于球的半径．‎ 式题 已知球的直径SC＝4，A，B是该球球面上的两点，且AB＝，∠ASC＝∠BSC＝30°，则棱锥SABC的体积为(　　)‎ A．3 B．2 C. D．1‎ 参考答案 ‎■ 核心知识聚焦 ‎1．2　[解析] 由三视图可知，此组合体的前半部分是一个底面半径为r，高为2r的半圆柱(水平放置)，后半部分是一个半径为r的半球，其中半圆柱的一个底面与半球的半个圆面重合，所以此几何体的表面积为2r·2r＋πr2＋πr2＋πr·2r＋2πr2＝4r2＋5πr2＝16＋20π，解得r＝2.‎ ‎2．2＋　[解析] 四面体的直观图如图所示，设O是AC的中点，则OP＝OB＝1，因此PB＝，于是S△PAB＝S△PBC＝×()2＝，S△PAC＝S△ABC＝×2×1＝1，故四面体的表面积S＝2×1＋2×＝2＋.‎ ‎ ‎ ‎3．‎138 cm2　[解析] 此几何体是由长方体与三棱柱组合而成的，其直观图如图，‎ 所以该几何体的表面积为2×(4×3＋6×3＋6×4)＋2××3×4＋4×3＋3×5－3×3＝138(cm2)．‎ ‎4. cm3　[解析] 该几何体为一个正方体和一个正四棱锥的组合体，故该几何体的体积V＝23＋×2×2×2＝(cm3)．‎ ‎5.＋π　[解析] 由三视图知，该几何体为一个半圆柱与一个三棱锥的组合体，其中半圆柱的底面圆的半径为1、高为2，三棱锥的底面为一个等腰直角三角形，斜边上的高为1，所以该几何体的体积V＝××2×1×1＋π×12×2＝＋π.‎ ‎6.π　[解析] 根据三视图可知几何体是圆柱与两个圆锥的组合体，其体积V＝π×12×2＋2××π×12×1＝π(m3)．‎ ‎7.　[解析] 旋转后的几何体为一个底面半径为1，高为2的圆柱挖去一个底面半径为1‎ ‎，高为1的圆锥，所求几何体的体积为π×12×2－π×12×1＝π.‎ ‎8.　[解析] 设新的底面半径为r，则π×52×4＋π×22×8＝πr2×4＋πr2×8 ，即πr2＝π＋32π，解得r＝.‎ ‎9．60°　[解析] 设圆锥的底面半径为r，高为h，母线为l，则其侧面积为πrl，过轴的截面面积为rh.由题意可知，＝2π，得＝，故圆锥的母线与轴的夹角为60°.‎ ‎10．144π　[解析] 如图所示，当OC⊥平面AOB时，三棱锥O ABC的体积最大，此时V三棱锥OABC＝V三棱锥CAOB＝S△AOB·R＝R3＝36，所以R＝6，所以S球＝4πR2＝144π.‎ ‎ ‎ ‎■ 考点考向探究 例1　D　[解析] 由题意，在正方体中还原四面体的直观图如图所示．故选D.‎ 变式题　A　[解析] 该几何体是正方体的一部分，易知选项A正确．‎ 例2　　＋＋1　[解析] 易知，该几何体是一个三棱锥，且该三棱锥的高为，底面为底边边长为2，高为1的等腰直角三角形，故易求得该几何体的体积和表面积分别为和＋＋1.‎ 变式题　84　　[解析] 原几何体为一个长、宽、高分别为6，3，5的长方体砍去一个高为3，底面为直角边分别为3，4的直角三角形的三棱锥，因此该几何体的体积为3×6×5－××3×4×3＝90－6＝84，表面积为2×(6×3＋5×3＋5×6)－×3×4×2－×3×3＋×3 ×＝.‎ ‎ 高考易失分题11 ‎ 范例　B　[解析] 其直观图如图所示，‎ 故所求体积为10×＝×10＝175.‎ 高考预测　B　[解析] 该几何体的直观图如图所示，其体积为 ××(1＋2)×2×＝.‎ 例‎3　‎A　[解析] 折起后的图形是棱长为1的正四面体，将其放在正方体中，其直观图如图所示．它可以看作是一个棱长为的正方体被截去四个角后得到的几何体，可求得该几何体的外接球的半径为×＝，故所求球的体积为×＝.‎ 变式题　C　[解析] 如图，设球心为O，△ABC的外心为O′.根据球的性质可知，OO′⊥平面ABC，且∠SBC＝∠SAC＝90°，所以BC＝AC＝2.在△ABC中，根据余弦定理得cos∠ACB＝＝，所以sin∠ACB＝.根据正弦定理得＝2r(r为△ABC外接圆半径)，所以r＝，所以OO′＝＝＝.所以棱锥SABC的体积为××2×2××＝.‎ ‎ ‎ ‎■ 教师备用例题 例1(配例1使用)[2015·全国卷Ⅱ] 一个正方体被一个平面截去一部分后，剩余部分的三视图如图所示，则截去部分体积与剩余部分体积的比值为(　　)‎ A. B. C. D. ‎[解析] D　几何体的直观图为正方体ABCDA1B‎1C1D1截去了一个三棱锥AA1B1D1，如图所示．易知V三棱锥AA1B1D1＝V正方体，所以＝，故选D.‎ ‎ ‎ 例2(配例2使用)[2015·陕西卷] 一个几何体的三视图如图所示，则该几何体的表面积为(　　)‎ A．3π B．4π C．2π＋4 D．3π＋4‎ ‎[解析] D　该几何体是底面半径为1、母线长为2的圆柱被其轴截面截开的半个圆柱，其表面积为×2π×1×2＋2××π×12＋2×2＝3π＋4.‎ 例3(配例2使用)[2015·全国卷Ⅰ] 《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图所示，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有(　　)‎ A．14斛 B．22斛 C．36斛 D．66斛 ‎[解析] B　由题意，题中图形为四分之一圆锥，设圆锥的底面半径为R，则由＝8得R＝，所以V米＝V圆锥＝××π××5＝≈(立方尺)，所以÷1.62≈21.95≈22(斛)．‎