志鸿优化设计2014高考数学湖南专用理一轮课时作业12函数模型及其应用 4页

www.ks5u.com 课时作业12　函数模型及其应用 一、选择题 ‎1．f(x)＝x2，g(x)＝2x，h(x)＝log2x，当x∈(4，＋∞)时，下列选项中正确的是(　　)．‎ A．f(x)＞g(x)＞h(x) B．g(x)＞f(x)＞h(x)‎ C．g(x)＞h(x)＞f(x) D．f(x)＞h(x)＞g(x)‎ ‎2．我国为了加强对烟酒生产的宏观管理，除了应征税收外，还征收附加税，已知某种酒每瓶售价为70元，不收附加税时，每年大约销售100万瓶；若每销售100元国家要征附加税x元(叫做税率x%)，则每年销售量将减少10x万瓶，如果要使每年在此项经营中所收取的附加税额不少于112万元，则x的最小值为(　　)．‎ A．2 B．6‎ C．8 D．10‎ ‎3．对于任意实数x，符号[x]表示x的整数部分，即[x]是不超过x的最大整数，例如[2]＝2；[2.1]＝2；[－2.2]＝－3，这个函数[x]叫做“取整函数”，它在数学本身和生产实践中有广泛的应用，那么[log31]＋[log32]＋[log33]＋…＋[log3243]的值为(　　)．‎ A．847 B．850‎ C．852 D．857‎ ‎4．某研究小组在一项实验中获得一组关于y，t之间的数据，将其整理后得到如下的散点图，下列函数中，最能近似刻画y与t之间的关系的是(　　)．‎ A．y＝2t B．y＝2t2‎ C．y＝t3 D．y＝log2t ‎5．某地区的一种特色水果上市时间仅能持续几个月，预测上市初期和后期会因供不应求使价格呈连续上涨的态势，而中期又将出现供大于求使价格连续下跌，为准确研究其价格走势，下面给出的四个价格模拟函数中合适的是(其中p，q为常数，且q＞1，x∈[0,5]，x＝0表示‎4月1日，x＝1表示‎5月1日，…以此类推)(　　)．‎ A．f(x)＝p·qx B．f(x)＝px2＋qx＋1‎ C．f(x)＝x(x－q)2＋p D．f(x)＝pln x＋qx2‎ ‎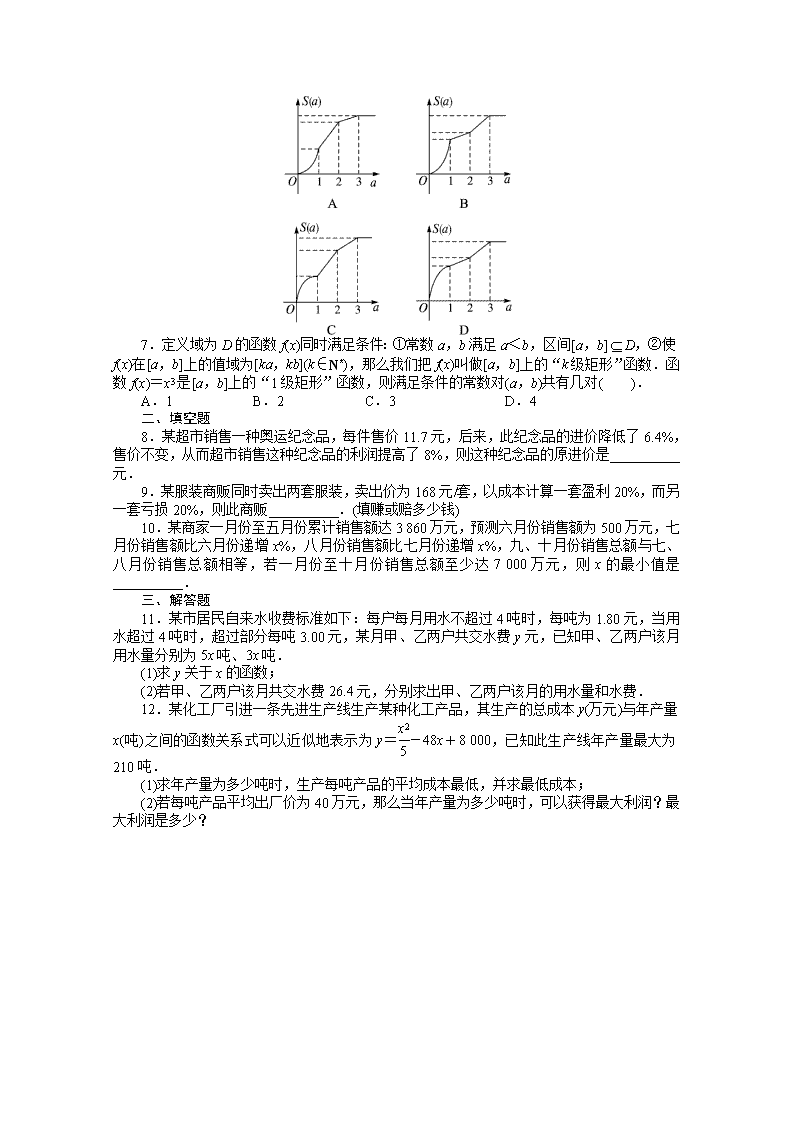6．图形M(如图所示)是由底为1，高为1的等腰三角形及高为2和3的两个矩形所构成的，函数S＝S(a)(a≥0)是图形M介于平行线y＝0及y＝a之间的那一部分面积，则函数S(a)的图象大致是(　　)．‎ ‎7．定义域为D的函数f(x)同时满足条件：①常数a，b满足a＜b，区间[a，b]D，②使f(x)在[a，b]上的值域为[ka，kb](k∈N*)，那么我们把f(x)叫做[a，b]上的“k级矩形”函数．函数f(x)＝x3是[a，b]上的“1级矩形”函数，则满足条件的常数对(a，b)共有几对(　　)．‎ A．1 B．‎2 ‎ C．3 D．4‎ 二、填空题 ‎8．某超市销售一种奥运纪念品，每件售价11.7元，后来，此纪念品的进价降低了6.4%，售价不变，从而超市销售这种纪念品的利润提高了8%，则这种纪念品的原进价是__________元．‎ ‎9．某服装商贩同时卖出两套服装，卖出价为168元/套，以成本计算一套盈利20%，而另一套亏损20%，则此商贩__________．(填赚或赔多少钱)‎ ‎10．某商家一月份至五月份累计销售额达3 860万元，预测六月份销售额为500万元，七月份销售额比六月份递增x%，八月份销售额比七月份递增x%，九、十月份销售总额与七、八月份销售总额相等，若一月份至十月份销售总额至少达7 000万元，则x的最小值是__________．‎ 三、解答题 ‎11．某市居民自来水收费标准如下：每户每月用水不超过4吨时，每吨为1.80元，当用水超过4吨时，超过部分每吨3.00元，某月甲、乙两户共交水费y元，已知甲、乙两户该月用水量分别为5x吨、3x吨．‎ ‎(1)求y关于x的函数；‎ ‎(2)若甲、乙两户该月共交水费26.4元，分别求出甲、乙两户该月的用水量和水费．‎ ‎12．某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y＝－48x＋8 000，已知此生产线年产量最大为210吨．‎ ‎(1)求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；‎ ‎(2)若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？‎ 参考答案 一、选择题 ‎1．B　解析：画出三个函数的图象，如图所示，当x∈(4，＋∞)时，指数函数的图象位于二次函数的图象的上方，二次函数的图象位于对数函数图象的上方，故g(x)＞f(x)＞h(x)．‎ ‎2．A　解析：由(100－10x)·70·≥112，‎ 解得2≤x≤8.所以x的最小值为2.‎ ‎3．D　解析：根据取整函数的定义，结合对数运算可得：[log31]～[log32]均为0；[log33]～[log38]均为1；[log39]～[log326]均为2；[log327]～[log380]均为3；[log381]～[log3242]均为4；[log3243]＝5.‎ 所以原式＝(2－0)×0＋(8－2)×1＋(26－8)×2＋(80－26)×3＋(242－80)×4＋5＝857.‎ ‎4．D　解析：此曲线符合对数函数的变化趋势．‎ ‎5．C　解析：由题意，排除A，B，对于选项C，f′(x)＝3x2－4qx＋q2，令f′(x)＝0，x＝q或，且q和都大于零，x＜或x＞q时f(x)单调递增，＜x＜q时f(x)单调递减，满足题意，对于D，f′(x)＝＋2qx，令f′(x)＝0，此方程无实根或有两异号根，不合题意．‎ ‎6．C　解析：依题意，当a≤1时，‎ S(a)＝＋‎2a＝－a2＋‎3a；‎ 当1＜a≤2时，S(a)＝＋‎2a；‎ 当2＜a≤3时，S(a)＝＋2＋a＝a＋；‎ 当a＞3时，S(a)＝＋2＋3＝，‎ 于是S(a)＝ 由解析式可知选C.‎ ‎7．C　解析：∵f(x)＝x3在[a，b]上单调递增，∴f(x)的值域为[a3，b3]．‎ 又函数f(x)＝x3是[a，b]上的“1级矩形”函数，‎ 则有解得或或 因此，满足条件的常数对(a，b)共有3对．‎ 二、填空题 ‎8．6.5　解析：设原进价为x元，则依题意有(11.7－x)(1＋8%)＝11.7－(1－6.4%)x，解得x＝6.5.‎ ‎9．赔14元　解析：设盈利的那套服装成本价为x，则x＋20%x＝168，x＝140，‎ 设亏损的那套服装成本价为y，‎ 则y－20%y＝168，y＝210，‎ 所以商贩赔(210－168)－(168－140)＝14(元)．‎ ‎10．20　解析：由题意得，3 860＋500＋[500(1＋x%)＋500(1＋x%)2]×2≥7 000，‎ 化简得(x%)2＋3·x%－0.64≥0，‎ 解得x%≥0.2，或x%≤－3.2(舍去)．‎ ‎∴x≥20，即x的最小值为20.‎ 三、解答题 ‎11．解：(1)当甲户的用水量不超过4吨时，即x≤，乙户的用水量也不超过4吨，y＝(5x＋3x)×1.8＝14.4x；‎ 当甲户的用水量超过4吨，乙户的用水量不超过4吨时，‎ 即＜x≤，‎ y＝4×1.8＋3x×1.8＋3×(5x－4)＝20.4x－4.8，‎ 当乙户的用水量超过4吨时，即x＞，‎ y＝8×1.8＋3×(8x－8)＝24x－9.6，‎ 所以y＝ ‎(2)由(1)可知y＝f(x)在各段区间上均为单调递增，‎ 当x∈时，‎ y≤f＝11.52＜26.4；‎ 当x∈时，‎ y≤f＝22.4＜26.4；‎ 当x∈时，‎ 令24x－9.6＝26.4，解得x＝1.5，‎ 所以甲户用水量为5x＝7.5吨，‎ 付费S1＝4×1.8＋3.5×3＝17.70(元)；‎ 乙户用水量为3x＝4.5吨，付费S2＝4×1.8＋0.5×3＝8.70(元)．‎ ‎12．解：(1)每吨平均成本为(万元)．‎ 又＝＋－48‎ ‎≥2－48＝32，‎ 当且仅当＝，即x＝200时，取等号．‎ ‎∴年产量为200吨时，每吨平均成本最低，最低为32万元．‎ ‎(2)设总利润为R(x)万元．‎ 则R(x)＝40x－y＝40x－＋48x－8 000＝－＋88x－8 000＝－(x－220)2＋1 680(0＜x≤210)，‎ ‎∵R(x)在(0,210]上是增函数，‎ ‎∴x＝210时，R(x)有最大值为 ‎－(210－220)2＋1 680＝1 660(万元)，‎ ‎∴年产量为210吨时，可获得最大利润1 660万元．‎